نمودار ون – از صفر تا صد

نمودار وِن را جان وِن (John Venn)، فیلسوف و منطق‌دان بریتانیایی، به عنوان راهی برای بیان بصری رابطه بین گروه‌های مختلف از اشیا اختراع کرد. از آنجایی که معادل ریاضی «یک گروه از اشیا» معادل با «یک مجموعه» است، با استفاده از نمودار ون می‌توان روابط بین مجموعه‌ها را نشان داد.

رسم نمودار ون

برای رسم یک نمودار ون، ابتدا یک مستطیل را می‌کشیم که «جهان» (Universe) یا مجموعه جهانی نامیده می‌شود. منظور از مجموعه جهانی، مجموعه‌ای نیست که همه چیز در آن وجود دارد، بلکه مجموعه‌ای است که همه چیزهایی که ما اکنون با آن سر و کار داریم در آن وجود دارند.

با توجه به این‌که این نمودار و رسم آن نیز یکی از دروس ریاضی نهم به حساب می‌آید، برای آشنایی بیشتر با این درس، مطالعه مطالب  زیر پیشنهاد می‌شود.

• تدریس فصل اول ریاضی نهم — راهنمای کامل + منابع رایگان
• فرمول های ریاضی نهم در یک نگاه و با مثال

مثال ۱

برای مثال موش‌ها، قوها، راسوها، غازها، کرم‌ها، اسب‌ها، گربه‌ها و نوک‌اردکی‌ها را در نظر بگیرید. مجموعه جهانی مربوط به این چیزها که با آن سر و کار داریم، مجموعه «حیوانات» است. مجموعه جهانی حیوانات را به صورت زیر رسم می‌کنیم.

اکنون می‌خواهیم حیواناتی را که نام بردیم در دو گروه یا مجموعه حیوانات «کوچک و خزدار» و «نوک‌دار» دسته‌بندی کنیم. برای رسم نمودار ون این دو مجموعه، دو دایره رسم می‌کنیم که هر کدام از آن‌ها متناظر با یکی از دو مجموعه‌ای است که نام بردیم.

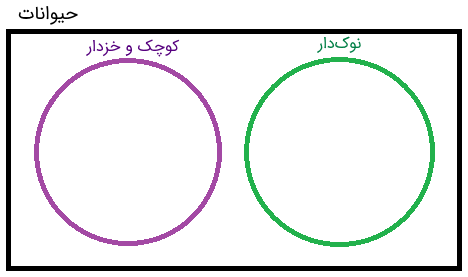
اکنون نام حیوانات مربوط به هر مجموعه را در داخل دایره‌های مربوطه می‌نویسیم.

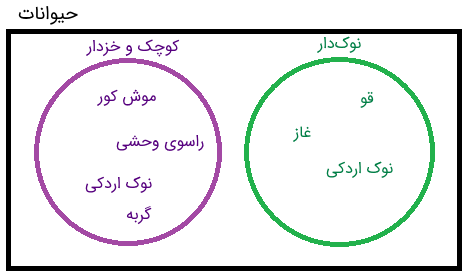
کرم‌ها کوچک هستند، اما خزدار نیستند و اسب‌ها خزدار هستند، اما کوچک نیستند. همچنین، هیچکدام از این دو نوک‌دار نیستند. با اینکه این دو حیوان در دو مجموعه مذکور قرار ندارند، اما در مجموعه جهانی ما وجود دارند. شکل زیر، این موضوع را به خوبی نشان می‌دهد.

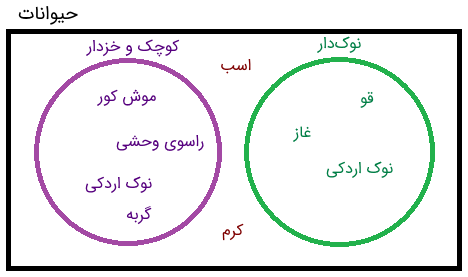
همان‌طور که می‌بینیم، نوک‌اردکی در هر دو دایره قرار دارد و بین آن‌ها «مشترک» است. در این موارد، اشتراک را در نمودار ون به صورت همپوشانی دایره‌ها نشان می‌دهیم. شکل زیر، گویای این موضوع است.

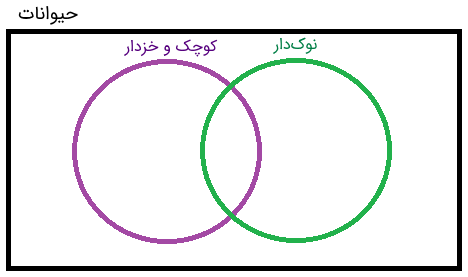
اکنون نمودار بالا را با نوشتن اسم حیواناتی که نام بردیم، تکمیل می‌کنیم و در قسمتی که دو نمودار با یکدیگر همپوشانی و اشتراک دارند، نوک‌اردکی را می‌نویسیم.

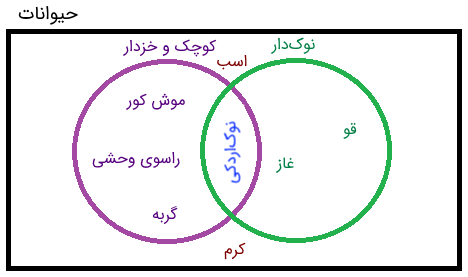
همان‌طور که در شکل بالا می‌بینیم، دو دایره (مجموعه‌های «نوک‌دار» و «کوچک و خزدار») یک اشتراک (نوک‌اردکی) دارند.

وقتی نمودارهای ون را رسم می‌کنیم، ممکن است تعداد دایره‌ها زیاد بوده و با یکدیگر چند همپوشانی داشته باشند.

فیلم آموزش روش حل نمودار ون + مثال‌های کاربردی (رایگان) در فرادرس

کلیک کنید

نمودارهای ون دو کاربرد اصلی دارند: توصیف مجموعه‌ها و دسته‌بندی مسائل دنیای واقعی. در ادامه، این کاربردها را بیان می‌کنیم.

توصیف مجموعه‌ها با نمودار ون

همان‌طور که گفتیم، با استفاده از نمودارهای ون می‌توان روابط بین مجموعه‌های مختلف را به خوبی بیان کرد. مثال زیر به درک این موضوع کمک می‌کند.

مثال ۲

فرض کنید مجموعه جهانی شامل اعداد ۱، ۲، ۳ و ۴ باشد. این مجموعه را به صورت $$\text {U} = \{ 1 , 2 , 3 , 4 \}$$ نشان می‌دهیم. مجموعه A را در نظر می‌گیریم که شامل اعداد ۱ و ۲ است. همچینین فرض می‌کنیم مجموعه B از اعداد ۲ و ۳ تشکیل شده است. بنابراین، داریم:

$$\text{A} = \{ 1 , 2 \}, \;\;\;\;\; \text{B} = \{ 2 , 3 \}$$

با کمک نمودار ون می‌توانیم روابط مختلف بین این مجموعه‌ها را به خوبی پیدا کنیم. نمودار ون مجموعه‌‌های B ،A و U به صورت زیر است.

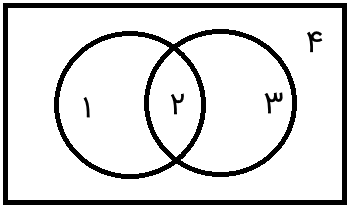
در ادامه، اجتماع، اشتراک، مکمل و تفاضل مجموعه‌ها را در قالب نمودار ون توضیح خواهیم داد.

A ∪ B

اجتماع A و B به مجموعه‌ای می‌انجامد که اعضای A یا B در آن وجود دارند. طبق این تعریف، نمودار ون اجتماع این دو مجموعه به صورت زیر است.

$$\text{A} \cup \text{B} = \{1, 2 , 3 \}$$

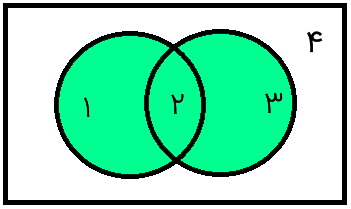
A ∩ B

اشتراک A و B مجموعه‌ای است که اعضای آن هم در A و هم در B وجود دارند، به عبارت دیگر، بین A و B مشترک هستند. بنابراین، نمودار ون دو مجموعه A و B به صورت زیر خواهد بود.

$$\text{A} \cap \text{B} = \{2 \}$$

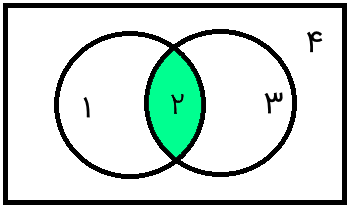
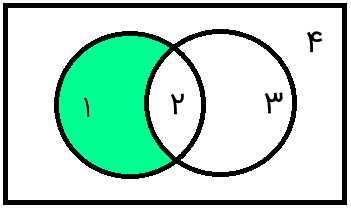
A^c

مکمل A که آن را با $$\text{A} ^ \text{c}$$ یا $$\sim \text{A}$$ یا $$¬ \text{A}$$ نمایش می‌دهند، مجموعه‌ای را نشان می‌دهد که اعضای آن همه مجموعه جهانی هستند، به جز اعضای خود A. به عبارت دیگر، می‌توان مکمل A‌ را به صورت $$\text{U}-\text{A}$$ نوشت. بنابراین، مکمل A به صورت زیر نمایش داده می‌شود.

$$\text{A} ^ \text{c} = \{ 3 , 4 \}$$

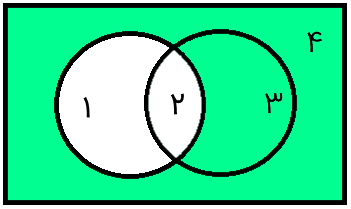
A-B

مجموعه A منهای B مجموعه‌ای است که اعضای آن شامل اعضای A هستند، به جز اعضایی که در B نیز وجود دارند. نمودار ون شکل زیر این موضوع را به خوبی نشان می‌دهد.

$$\text{A} - \text{B} = \{ 1 \}$$

همان‌طور که دیدیم، با استفاده از نمودار ون به راحتی می‌توان جبر مجموعه‌ها را انجام داد. برای روابط پیچیده‌تر نیز می‌توانیم از این نمودار استفاده کنیم.

برای مثال، نمودار ون مربوط به $$\sim ( \text {A} \cup \text{B})$$ مطابق شکل زیر است.

$$\sim ( \text {A} \cup \text{B}) = \{ 4 \}$$

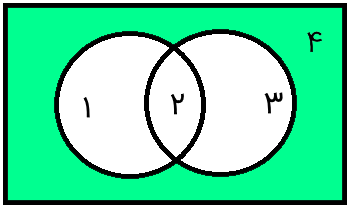
همچنین، نمودار ون مربوط به $$\sim ( \text {A} \cap \text{B})$$ به صورت زیر است.

$$\sim ( \text {A} \cap \text{B}) = \{ 1, 3 , 4 \}$$

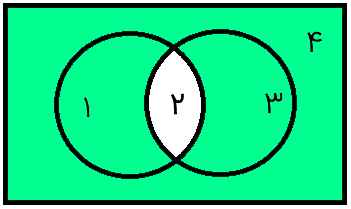
برای تعداد مجموعه‌های بیشتر و بزرگ‌تر نیز می‌توان از نمودار ون کمک گرفت.

کاربرد نمودار ون در دنیای واقعی

همان‌طور که گفتیم، می‌توان مسائل دنیای واقعی را با نمودار ون بیان کرد و دسته‌بندی مناسبی برای آن‌ها انجام داد. در ادامه، مثالی را در این باره ارائه می‌کنیم.

فیلم آموزش مبانی منطق و نظریه مجموعه ها در فرادرس

کلیک کنید

مثال ۳

فرض کنید ۴۰ دانش‌آموز در مدرسه‌ای هستند که ۱۴ نفر از آن‌‌ها در کلاس ریاضی و ۲۹ نفرشان در کلاس شیمی شرکت می‌کنند. فرض می‌کنیم پنج دانش‌آموز در هر دو کلاس باشند. می‌خواهیم به پرسش‌های زیر پاسخ دهیم:

(الف) چه تعداد از دانش‌آموزان در هیچ‌کدام از کلاس‌ها نیستند؟

(ب) چه تعداد از دانش‌آموزان در هر دو کلاس هستند؟

(ج) اگر دانش‌آموزی را به صورت تصادفی از این گروه انتخاب کنیم، احتمال آنکه فقط در کلاس شیمی حضور داشته باشد چقدر است؟

دو مجموعه در مجموعه جهانی داریم: دانش‌آموزان کلاس ریاضی و دانش‌آموزان کلاس شیمی.

ابتدا مجموعه جهانی را رسم می‌کنیم که همان ۴۰ دانش‌آموز هستند. دو مجموعه بالا را نیز در داخل آن رسم می‌کنیم.

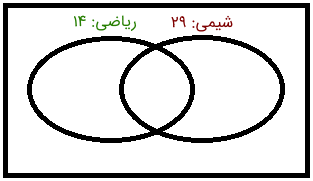
پنج دانش‌آموز در هر دو کلاس شرکت کرده‌اند. بنابراین، اشتراک یا همان همپوشانی دو مجموعه پنج نفر است. آن را به صورت زیر مشخص می‌کنیم.

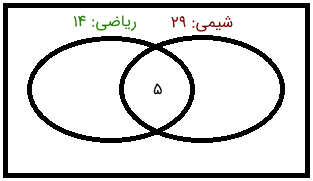
اکنون اگر پنج دانش‌آموز را از کلاس ریاضی فرض کنیم، ۹ دانش‌آموز دیگر در این کلاس باقی می‌مانند.

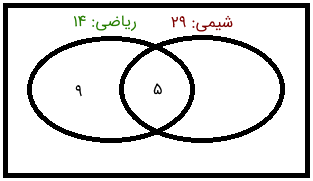
چون پنج دانش‌آموز در کلاس شیمی نیز حضور دارند، ۲۴ دانش‌آموز باقی می‌مانند که فقط در کلاس شیمی هستند.

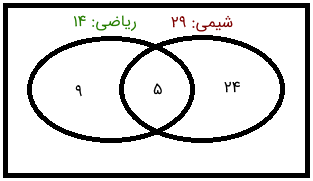
نمودار ون بالا به ما می‌گوید که $$9 + 5 + 24 = 38$$ دانش‌آموز در کلاس شیمی یا ریاضی (یا هر دو) هستند. این عدد پاسخ پرسش دوم را به ما می‌دهد و می‌توانیم بگوییم که ۳۸ دانش‌اموز در هر دو کلاس هستند. احتمالاً این ابهام برایتان پیش آمده است که ۲ دانش‌آموز را از قلم انداخته‌ایم. پاسخ این ابهام این است که این دو دانش‌آموز عضو مجموعه جهانی هستند و در هیچ‌کدام از دو مجموعه مورد نظر وجود ندارند. بنابراین، نمودار ون به صورت زیر تکمیل خواهد شد.

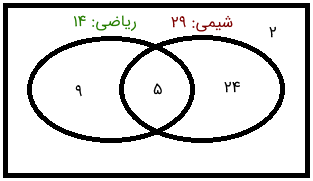
اما پرسش آخر در این مثال این است که اگر دانش‌آموزی را به صورت تصادفی از بین دانش‌آموزان انتخاب کنیم، احتمال آنکه فقط در کلاس شیمی حضور داشته باشد چقدر است؟ از 40 دانش‌اموز، 24 نفرشان فقط در کلاس شیمی حضور دارند. بنابراین، احتمال مورد نظر برابر است با:

$$\frac { 24 } { 40 } = 0.6 = 60 \%$$

در نهایت، پاسخ سه پرسش را می‌توان به صورت زیر خلاصه کرد:

پاسخ (لف): ۲ دانش‌آموز در هیچ کلاسی نیستند.

پاسخ (ب): ۳۸ دانش‌آموز حداقل در یک کلاس حضور دارند.

پاسخ (ج): به احتمال ۶۰ درصد اگر دانش‌آموزی را به طور تصادفی انتخاب کنیم، در کلاس شیمی هست و در کلاس ریاضی نه.

مثال ۴

مثال دیگری را در نظر بگیرید. فرض کنید شخصی به مسافرت رفته و پس از مدتی به خانه‌اش برگشته است. او روی فرش تعدادی مارمولک می‌بیند و متوجه می‌شود که گربه‌اش در نبود او به مارمولک‌ها حمله کرده و اتفاقاتی را برای آن‌ها رقم زده است. او موارد زیر را روی فرش مشاهده کرده است:

• شش مارمولک کبود
• دوازده مارمولک که سعی بر فرار از گربه داشته‌اند و دم خود را از دست داده‌اند.
• پانزده مارمولک که جویده شده‌اند.

علاوه بر این:

• فقط یکی از مارمولک‌ها کبود بوده، جویده شده و دم‌بریده است.
• دو مارمولک کبود و دم‌بریده هستند، اما جویده نشده‌اند.
• دو مارمولک کبود هستند و جویده شده‌اند، اما دم‌بریده نیستند.

اگر ۲۴ مارمولک روی فرش باقی مانده باشند، و همه آن‌ها حداقل یکی از ویژگی‌های «کبود بودن»، «دم‌بریده بودن» و «جویده شدن» را داشته باشند، چه تعداد از مارمولک‌ها دم‌بریده و جویده شده هستند، اما خاکستری نیستند؟

با توجه به اطلاعات مسئله، گام به گام پیش می‌رویم.

اولین اطلاعاتی که درباره مسئله داریم، این است که همه مارمولک‌ها حداقل یک ویژگی را دارند. این بدین معنی است که چیزی خارج از دایره‌ها وجود ندارد.

همچنین، یک مارمولک وجود دارد که دارای هر سه ویژگی است و در هر سه مجموعه قرار دارد.

بنابراین، نمودار ون باید به گونه‌ای باشد که در آن، هر سه دایره اشتراک و همپوشانی داشته باشند. این اشتراک را با عدد یک در محل همپوشانی آن‌ها نشان می‌دهیم که همان مارمولک مذکور را نشان می‌دهد.

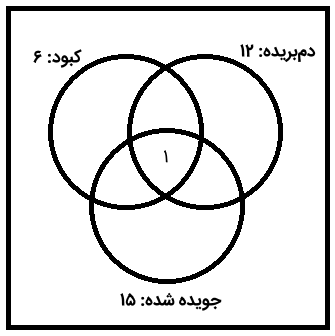
دو مارمولک از مارمولک‌ها کبود و دم‌بریده هستند، اما جویده نشده‌اند. بنابراین، عدد ۲ را در ناحیه اشتراک بین «کبود» و «دم‌بریده» قرار می‌دهیم.

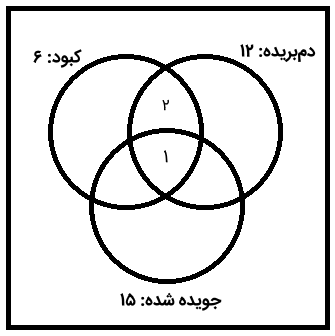
دو تا از مارمولک‌ها نیز کبود و جویده‌ شده‌اند، اما دم‌بریده نیستند؛ بنابراین، یک عدد ۲ نیز در محل اشتراک کبود و جویده شده نیز قرار می‌دهیم.

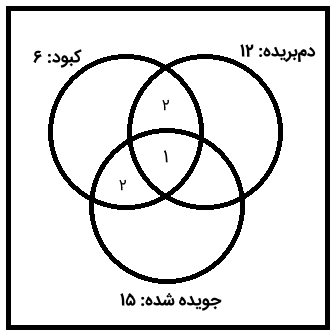
از آنجایی که تعداد همه مارمولک‌های کبود شش بود و پنج تا از آن‌ها را به حساب آوردیم، یکی از آن‌ها باقی می‌ماند که فقط کبود است. بنابراین، نمودار ون زیر را خواهیم داشت.

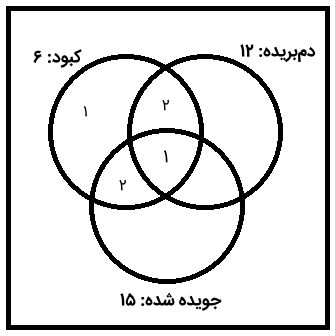
اطلاعات نمودار ون بالا به ما کمک خواهد کرد تا تعداد مارمولک‌هایی را که دم‌بریده و جویده شده بودند، اما کبود نبودند به دست آوریم. اما نمی‌دانیم چه تعداد مارمولک فقط جویده شده یا فقط دم‌بریده هستند. بنابراین، هنوز نمی‌توان درباره ناحیه اشتراک این دو اظهار نظر کرد.

بنابراین، به جای عدد اشتراک دو مجموعه مذکور، مقدار $$x$$ را قرار می‌دهیم که یک مقدار مجهول است و تعداد مارمولک‌های دم‌بریده و جویده شده را نشان می‌دهد.

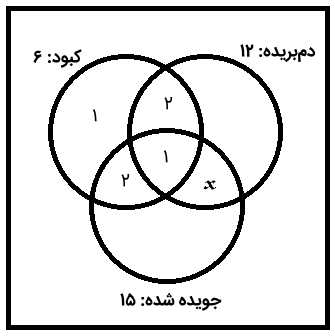
می‌دانیم که تعداد کل مارمولک‌های جویده شده ۱۵ و تعداد کل مارمولک‌های دم‌بریده ۱۲ است. با کم کردن همه اشتراکات، تعداد مارمولک‌هایی که فقط جویده شده‌اند، برابر است با:

$$15 - 2 - 1 - x = 12 - x$$

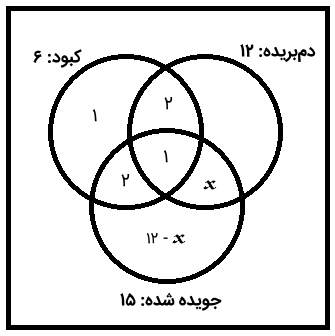
تعداد مارمولک‌هایی که فقط دم‌بریده هستند به صورت زیر است:‌

$$12 - 2 - 1 - x = 9 - x$$

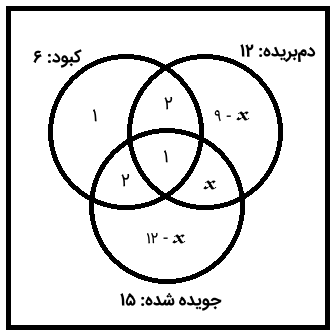
همان‌طور که گفتیم، تعداد همه مارمولک‌ها ۲۴ است، بنابراین، با جمع کردن بخش‌های مختلف دایره‌ها و برابر قرار دادن آن‌ها با این عدد، مقدار مجهول $$x$$ به دست می‌آید. مواردی را که با هم جمع می‌کنیم، اینگونه است: (هرچه در دایره کبود است) + (مقدار همپوشانی مجهول) + (تعداد مارمولک‌های فقط جویده شده) + (تعداد مارمولک‌های فقط دم‌بریده) یا:

$$(1+2+1+1) + (x) + (12-x) + (9 - x) = 27- x = 24$$

در نتیجه، مقدار ۳ برای $$x$$ حاصل می‌شود و پاسخ پرسش این‌گونه خواهد بود: ۳ تا از مارمولک‌ها دم‌بریده و جویده شده هستند، اما کبود نیستند.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• اصل لانه کبوتر — به زبان ساده
• اتحاد و تجزیه در ریاضی — به زبان ساده
• تجزیه کسر — به زبان ساده

^^