تابع همانی و خصوصیات آن | به زبان ساده
یکی از توابع خاص در ریاضیات، تابع همانی است که بخصوص در بحث آنالیز ریاضی و نظریه مجموعهها، نقش مهمی ایفا میکند. چنین تابعی به ازاء هر مقدار برای متغیر، مقدار تابع را همان عدد حقیقی (یا مختلط) نسبت میدهد. از این تابع برای اثبات یا ایجاد مثال نقض برای قضیههای مختلف آنالیز، استفاده میشود. همچنین این تابع را به عنوان عضو یکه در نظریه اعداد یا نظریه رستهها نیز میتوان به کار برد. به این جهت این نوشتار از مجله فرادرس را به تابع همانی و خصوصیات آن اختصاص دادهایم.
برای آشنایی بیشتر با موضوع توابع در ریاضیات بهتر است ابتدا نوشتارهای دیگر مجله فرادرس با عنوانهای رابطه و تابع از نگاه مجموعه ها — به زبان ساده و ضرب دکارتی مجموعه ها و مختصات دکارتی — به زبان ساده را مطالعه کنید. همچنین خواندن نوشتارهای مجموعه ها در ریاضیات – مفاهیم پایه و پیوستگی (Continuity) و تابع پیوسته (Continues Function) — به زبان ساده نیز خالی از لطف نیست.
تابع همانی و خصوصیات آن
همانطور که میشود حدس زد، تابع همانی (Identity Function)، هر مقدار را به خود آن، نگاشت یا تبدیل میکند. به این ترتیب تابع $$f$$ را یک تابع همانی مینامند، اگر پارامتر تابع با مقدار تابع برای همه اعضای دامنه، یکسان باشد. با توجه به این موضوع تابع $$f(x)=x$$ یک تابع همانی است، زیرا به ازاء هر مقدار از دامنه، نتیجه تابع همان مقدار است. مسلما باید از این رابطه نتیجه گرفت که دامنه و برد چنین تابعی یکسان است.
تعریف تابع همانی
به طور رسمی، اگر $$M$$ یک مجموعه بوده و تابع $$f$$ با ضابطه زیر، روی آن تعریف شده باشد، بطوری که دامنه و برد آن یکسان بوده و برابر با $$M$$ باشند، $$f$$ را تابع همانی مینامند.
$$ \large f(x) = x , \quad \quad \forall x \in M $$
به بیان دیگر تابع $$f(x)$$ در $$M$$، همیشه همان مقدار ورودی تابع خواهد بود. همانطور که دیده میشود، «همدامنه» (Codomain) و «دامنه تابع» (Domain) یکسان بوده و هر دو مجموعه $$M$$ هستند.

واضح است که تابع همانی، یک تابع یک به یک (Injective) است. همچنین آن را میتوان یک تابع پوشا (Surjective) نیز در نظر گرفت، در نتیجه چنین تابعی را میتوان «یک به یک و پوشا» (One to one correspanding)، در نتیجه «معکوسپذیر» (Invertable) دانست.
جالب است که معکوس تابع همانی، باز تابع همانی خواهد بود. معمولا تابع همانی روی مجموعه $$M$$ را به صورت $$id_M$$ نشان میدهند.
در نظریه مجموعه، تابعی همانی را به صورت یک «رابطه همانی» (Identity Relation) نیز در نظر میگیرند. همچنین میتوان چنین تابعی را به صورت یک رابطه دو دویی در نظر گرفته و عناصر قطری ماتریس $$M$$ را همان مقادیر تابع همانی منظور کرد. ماتریس حاصل از ضرب دکارتی مجموعه $$M$$ در خودش، عناصر این حاصل ضرب دو دویی در نظر گرفته میشوند.
$$ \large \begin{bmatrix}(1,1) & (1,2) & (1,3)& \cdots \\ (2,1) & (2,2) &(2,3)&\cdots \\ (3,1) & (3,2) &(3,3)&\cdots \\ \cdots&\cdots&\cdots&\cdots \end{bmatrix}$$
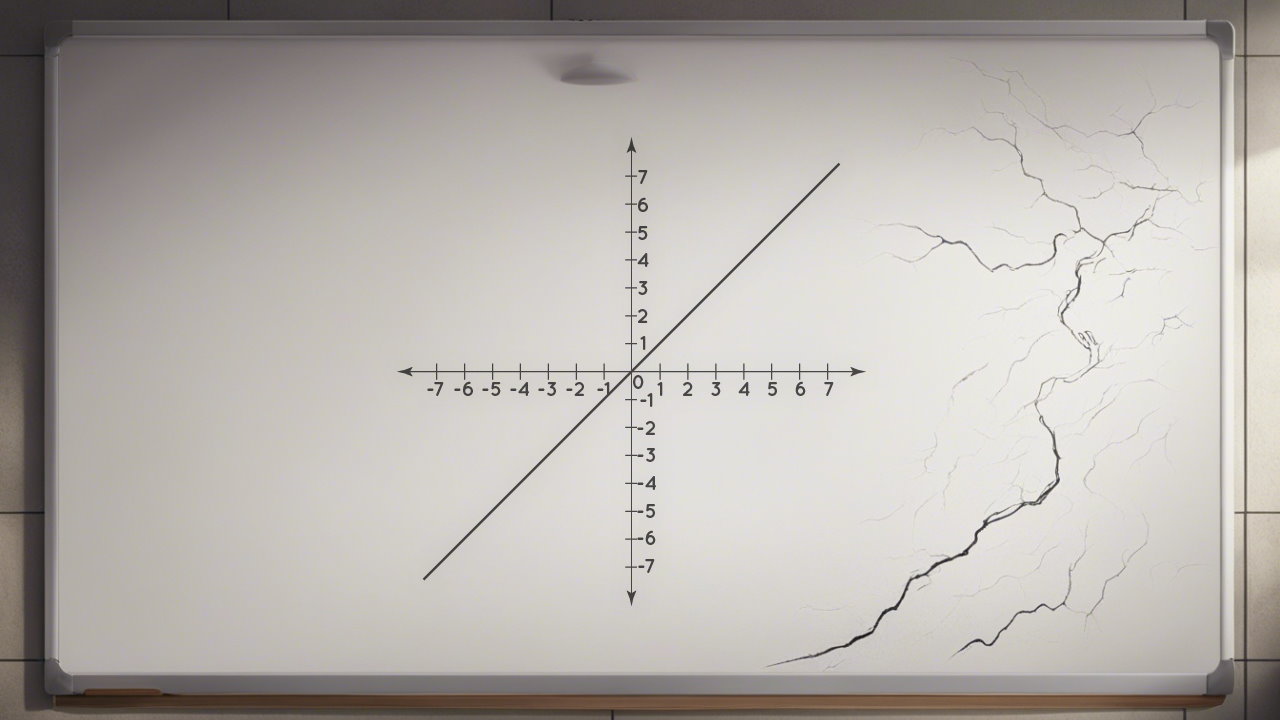
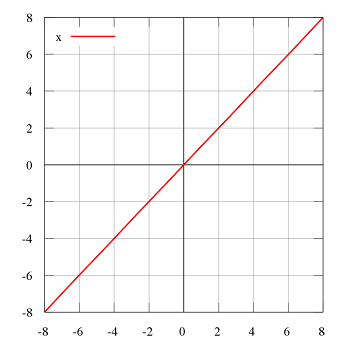
نمودار تابع همانی را براساس تعریف ارائه شده در تصویر زیر مشاهده میکنید. همانطور که مشخص است چنین تابعی، نیمساز ربع اول و سوم است. تابع همانی پیوسته و بدون هیچ نقطه شکست بوده و همه جا مشتقپذیر است.
خصوصیات جبری تابع همانی
فرض کنید که تابع $$f$$ از مجموعه $$M$$ به $$N$$ تعریف شده است.
$$ \large f: M \rightarrow N$$
در این صورت
$$ \large f \circ id_M = f $$
و
$$ \large id_N \circ f = f $$
بطوریکه عملگر $$\circ$$ نشانگر «ترکیب دو تابع» (Function Composition) است. به طور کلی $$id_M$$ یک عنصر همانی از «تَکوار» (Monoid) از $$M$$ به $$M$$ محسوب میشود.
نکته: منظور از «تَکوار» (Monoid)، یک مجموعه مانند $$S$$ به همراه یک عملگر دو دویی (مثل $$\cdot$$) است که دارای عضو خنثی است. بنابراین میتوان آن را یک «نیمگروه» (Semigroup) دانست که شامل عضو خنثی خواهد بود.
از آنجایی که عنصر همانی، در تَکوار، یکتا است، میتوان تعریف تابع همانی را روی $$M$$، همان عنصر همانی در عملگر دو دویی در نظر گرفت. چنین تعریفی میتواند مفهوم تابع همانی را به مفاهیمی مانند «یکریختی» (identity morphism) در تئوری و «نظریه رستهها» (Category Theory) تبدیل کند. این موضوع را در قسمت قبل، زمانی که تابع همانی را به صورت ترکیب با تابع $$f$$ به کار بردیم، مشاهده کردید.
خواص تابع همانی
در ادامه به بعضی از خواص تابع همانی به صورت فهرستوار توجه میکنیم.
- تابع همانی، یک تابع پیوسته روی دامنهاش است.
- برد و دامنه تابع همانی، یکسان است.
- تابع همانی، یک «عملگر خطی» (Linear Operator) در «فضای برداری» (Vector Space) محسوب میشود.
- تابع همانی، روی مجموعه اعداد صحیح مثبت (مقادیر شامل سمت راست محور اعداد حقیقی) یک «تابع ضربی کامل» (Completely Multiplicative Function) است. بخصوص زمانی که در نظریه اعداد، از مضرب ۱ استفاده کنیم.
- در فضای برداری $$n$$-بُعدی، تابع همانی، توسط «ماتریس یکه» (Identity Matrix) با نماد $$I_m$$، بدون در نظر گرفتن پایه (Basis)، ساخته میشود.
- در فضای برداری، تابع همانی، به صورت بدیهی، یک تابع متقارن محسوب میشود.
- در فضای تويولوژیک (Toplogic Space)، تابع همانی، همیشه پیوسته است.
- تابع همانی، یک تابع «خودتوان» (Idempotent) خواهد بود. به این معنی که با تکرار این تابع روی یک متغیر، نتیجه تغییر نکرده و همیشه مقدار تابع در نقطه $$x$$ را نمایش میدهد. پس رابطه زیر برقرار است.
$$ \large id \left( id(X) \right) = x $$
جالب است که با تکرار این عمل نیز تغییری در تابع همانی بوجود نخواهد آمد.

مشتق و انتگرال تابع همانی
همانطور که در نمودار این تابع مشخص است، شیب خط، همیشه یکسان بوده و زاویه این خط را محور افقی، ۴۵ درجه یا $$\pi/4$$ است. در نتیجه براساس معادله این خط، مقدار شیب خط یا تانژانت (Tangent) زاویه نمودار با محور افقی، برابر با ۱ خواهد بود.
به این ترتیب، از آنجایی که مشتق این تابع، شیب خط مماس را مشخص میکند، واضح است که مقدار مشتق روی همه دامنه تابع برابر با ۱ خواهد بود.
$$ \large \dfrac{d \left( f(x) \right)}{dx} = \dfrac{dx}{dx} = 1 $$
از طرفی انتگرال یا سطح زیر منحنی تابع همانی نیز براساس تصویر بالا، با مساحت مثلث قائمالزاویهای که براساس این تابع ساخته میشود، برابر است. در نتیجه اگر انتگرال این تابع را در بازه $$a$$ تا $$b$$ در نظر بگیریم، مساحت مثلث حاصل برابر است با:
$$ \large \dfrac{(b - a) \times (b - a)}{2} = \dfrac{(b - a)^2}{2} $$
حال اگر به کمک روشهای انتگرالگیری برای تابع $$f(x) = x$$ در همین بازه، محاسبات را انجام دهیم، به نتیجه زیر خواهیم رسید.
$$ \large \int_a^b x \; dx = \dfrac{x^2}{ 2 }|^b_a = \dfrac{(b - a)^2}{2} $$
که با نتیجه قبلی نیز سازگار است.
تابع همانی در فضای اعداد مختلط
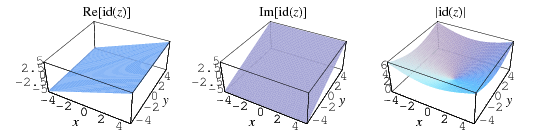
اگر دامنه تابع همانی را مجموعه اعداد مختلط در نظر بگیریم، آنگاه نمودار این تابع در بخش حقیقی $$Re[id(z)]$$، بخش موهومی $$Im[id(z)]$$ به شکل زیر خواهند بود. واضح است که برد چنین تابعی نیز همان اعداد مختلط خواهد بود.
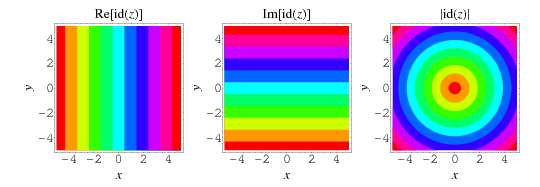
به این ترتیب نمودار یا نمایش کانتور چنین تابعی به مانند تصویر زیر در مختصات اعداد مختلط ترسیم میشود.
خلاصه و جمعبندی
در این نوشتار به تابع همانی توجه کرده و بعضی از ویژگیهای مهم آن مانند محاسبه مشتق و انتگرال را مورد بحث قرار دادیم. از طرفی تابع همانی را از فضای دو و چند بعدی نیز میتوان به فضای اعداد مختلط تعمیم داد که این موضوع در بخشی از مطلب مورد بررسی قرار گرفت. هر چند تابع همانی ساده به نظر میرسد ولی کاربردهای متنوعی در محاسبات، بخصوص در مباحث آنالیز ریاضی دارد.











استفاده کردم ممنونم