فرم نمایی و قطبی اعداد مختلط — به زبان ساده (+ دانلود فیلم آموزش رایگان)
پیشتر در سلسله آموزشهای ریاضی مجله فرادرس، با اعداد مختلط آشنا شدیم. دیدیم که معمولاً این اعداد را بهفرم $$z = a + bi$$ مینویسند. اما، فرمهای مفید دیگری نیز وجود دارند که میتوان اعداد مختلط را مطابق آنها نوشت و محاسبات را سادهتر و سریعتر کرد. در این آموزش، «فرم قطبی» (Polar Form) و «فرم نمایی» (Exponential Form) اعداد مختلط را معرفی میکنیم.
تفسیر هندسی
پیش از اینکه درباره نمایش اعداد مختلط به فرمهای دیگر بحث کنیم، تفسیر هندسی این اعداد را بهصورت اجمالی بررسی میکنیم.
عدد مختلط $$z=a+ bi$$ را در نظر بگیرید. این عدد را میتوانیم بهعنوان نقطه $$(a,b)$$ در دستگاه مختصات کارتزین استاندارد یا بهعنوان برداری که از مبدا شروع شده و پایان آن در نقطه $$(a, b)$$ است، در نظر بگیریم. شکل زیر، این موضوع را بهخوبی نشان میدهد.
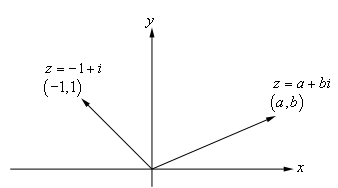
در شکل بالا، محور $$x$$، محور حقیقی و محور $$y$$، محور موهومی است. اغلب، صفحه $$xy$$ را صفحه مختلط مینامیم.
با توجه به شکل بالا میتوانیم اندازه عدد مختلط را تعریف کنیم. از شکل مذکور واضح است که $$\left| z \right| = \sqrt {{a^2} + {b^2}}$$ چیزی جز طول بردار نیست که برای نمایش عدد مختلط از آن استفاده کردهایم. تفسیر هندسی اعداد مختلط به ما میگوید که نامساوی $$\left| {{z_1}} \right| < \left| {{z_2}} \right|$$ به این معنی است که $$z_1$$ به مبدا صفحه مختلط نزدیکتر است.
فرم قطبی
در این بخش، یکی از فرمهای نمایش اعداد مختلط را بیان میکنیم.
عدد مختلط غیرصفر $$a+bi$$ را بهعنوان نقطه $$(a,b)$$ در صفحه $$xy$$ در نظر بگیرید. این نقطه را میتوان در دستگاه مختصات قطبی $$(r, \theta)$$ نشان داد که در آن، $$r$$ فاصله نقطه از مبدا و $$\theta$$ زوایه نسبت به محور مثبت $$x$$ و برحسب رادیان است.
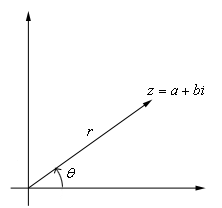
هنگام کار با اعداد مختلط، فرض میکنیم $$r$$ مثبت است و $$\theta$$ میتواند هر زاویه ممکنی (مثبت و منفی) باشد. این بدین معنی است که بینهایت انتخاب برای تعیین $$\theta$$ وجود دارد (جزئیات آن را در ادامه بیان میکنیم). البته $$z=0$$، از این قاعده مستثنی است. زیرا $$\theta$$ در مبدا تعریف نشده است. بنابراین، فرم قطبی را برای اعداد اعداد مختلط غیرصفر در نظر میگیریم.
فرمول تبدیل زیر را میتوان برای تبدیل نقطهای با مختصات قطبی $$(r, \theta)$$ به مختصات کارتزین $$(a, b)$$ بهکار برد:
$$a = r\cos \theta \hspace{0.75in} b = r\sin \theta$$
اگر عدد مختلط را $$z=a+bi$$ تعریف کنیم، شکل قطبی آن بهصورت زیر خواهد بود:
$$\begin{equation}z = r\left( {\cos \theta + i\sin \theta } \right) \end{equation}$$
مقدار $$r$$ را میتوان برحسب $$a$$ و $$b$$ بهصورت زیر محاسبه کرد:
$$r = \sqrt {{a^2} + {b^2}}$$
مقدار $$r$$ در حقیقت همان اندازه $$z$$ است و میتوان عدد مختلط را بهصورت زیر نوشت:
$$\begin{equation}z = \left| z \right|\left( {\cos \theta + i\sin \theta } \right)\end{equation}$$
زاویه $$\theta$$، آرگومان $$z$$ نام دارد و بهصورت زیر نوشته میشود:
$$\theta = \arg z$$
آرگومان $$z$$ میتواند یکی از بینهایت مقدار $$\theta$$ باشد که از حل رابطه زیر بهدست میآید:
$$\begin{equation}\tan \theta = \frac{b}{a}\end{equation}$$
این تعداد آرگومان بینهایت، بهاندازه ضریب صحیحی از $$2\pi$$ با هم تفاوت دارند.
گفتیم برای انتخاب آرگومان یک عدد مختلط، بینهایت انتخاب وجود دارد و همه این انتخابها بهاندازه $$2\pi$$ نسبت به هم اختلاف دارند. به عبارت دیگر، اگر $$\theta$$ پاسخ برای آرگومان عدد مختلط باشد، مقدار $$\theta+ 2\pi$$ نیز یک پاسخ است، زیرا بهاندازه یک دور کامل در خلاف جهت عقربههای ساعت حرکت کرده و به همان نقطه $$\theta$$ رسیده است. شکل زیر این موضوع را نشان میدهد.

اگر یک دور دیگر بزنیم و باز هم به نقطه مورد نظر برسیم، آرگومان زاویه برابر با $$\theta+4\pi$$ خواهد بود. برای دور زدن در جهت عقربههای ساعت نیز نتایج مشابه است. به همین ترتیب میتوان گفت بینهایت آرگومان وجود دارد.
با توجه به بحث بالا، اگر دو زاویه $$\theta _1$$ و $$\theta _2$$، دو مقدار برای آرگومان $$z$$ باشند، آنگاه عدد صحیح $$k$$ وجود دارد که در رابطه زیر صدق میکند:
$$\begin{equation}{\theta _1} - {\theta _2} = 2\pi k\end{equation}$$
مقدار اصلی آرگومان که آرگومان اصلی نیز نامیده میشود، یک مقدار منحصربهفرد از آرگومان است که در محدوده $$- \pi < \arg z \le \pi$$ قرار دارد و با $${\mathop{\rm Arg}\nolimits} z$$ مشخص میشود. از نامعادله اخیر میتوان نتیجه گرفت که آرگومان اصلی یک عدد حقیقی منفی برابر با $${\mathop{\rm Arg}\nolimits} z = \pi$$ است.
مثال
فرم قطبی هریک از اعداد مختلط زیر را بنویسید:
- (الف) $$z = - 1 + i\,\sqrt 3$$
- (ب) $$z = - 9$$
- (ج) $$z = 12\,i$$
حل:
(الف) ابتدا مقدار $$r$$ را بهدست میآوریم:
$$r = \left| z \right| = \sqrt {1 + 3} = 2$$
اکنون باید آرگومان $$z$$ را محاسبه کنیم. گفتیم که آرگومان اصلی باید در بازه $$- \pi < \theta \le \pi$$ باشد. با استفاده از رابطه زیر میتوان مقدار آرگومان را بهدست آورد:
$$\tan \theta = \frac{{\sqrt 3 }}{{ - 1}} \hspace{0.25in} \Rightarrow \hspace{0.25in} \theta = {\tan ^{ - 1}}\left( { - \sqrt 3 } \right)$$
اگر از ماشین حساب استفاده کنید، پاسخی در محدوده $$- \frac{\pi }{2} < \theta < \frac{\pi }{2}$$ به شما خواهد داد. اگر ماشین حساب عدد $$\theta _1$$ را بهعنوان پاسخ نشان دهد، زاویه $$\theta _2=\theta _1+ \pi$$ نیز ممکن است آرگومان اصلی باشد. این دو مقدار را باید بررسی کنید. در این مثال، داریم:
$${\theta _1} = - \frac{\pi }{3} \hspace{0.25in} {\theta _2} = - \frac{\pi }{3} + \pi = \frac{{2\pi }}{3}$$
مقدار نخست، در ربع چهارم و مقدار دوم در ربع دوم قرار دارد. با توجه به مقادیر $$a$$ و $$b$$ که در ربع دوم قرار دارند، مقدار دوم را برای آرگومان اصلی انتخاب میکنیم. بنابراین، آرگومان اصلی برابر است با:
$${\mathop{\rm Arg}\nolimits} \,z = \frac{{2\pi }}{3}$$
سایر مقادیر ممکن آرگومان نیز بهصورت زیر است:
$$\arg z = \frac{{2\pi }}{3} + 2\pi n \hspace{0.25in} n = 0, \pm 1, \pm 2, \ldots$$
اکنون میتوانیم عدد مورد نظر را به فرم قطبی زیر بنویسیم:
$$z = 2\left( {\cos \left( {\frac{{2\pi }}{3}} \right) + i\sin \left( {\frac{{2\pi }}{3}} \right)} \right)$$

برای دو مورد آرگومان دیگر، داریم:
$$\begin{align*}z & = 2\left( {\cos \left( {\frac{{8\pi }}{3}} \right) + i\sin \left( {\frac{{8\pi }}{3}} \right)} \right) & \hspace{0.25in} & n = 1\\
z & = 2\left( {\cos \left( { - \frac{{16\pi }}{3}} \right) + i\sin \left( { - \frac{{16\pi }}{3}} \right)} \right) & \hspace{0.25in} & n = - 3\end{align*}$$
(ب) گفتیم که آرگومان اصلی اعداد حقیقی منفی را برابر با $$\pi$$ در نظر میگیریم. سایر آرگومانهای این عدد، بهصورت زیر است:
$$\arg z = \pi + 2\pi n = \pi \left( {1 + 2n} \right) \hspace{0.25in} n = 0, \pm 1, \pm 2, \ldots$$
اکنون، مقدار $$r$$ را محاسبه میکنیم:
$$r = \left| z \right| = \sqrt {81 + 0} = 9$$
در نتیجه، فرم قطبی عدد (با آرگومان اصلی) بهصورت زیر است:
$$z = 9\left( {\cos \left( \pi \right) + i\sin \left( \pi \right)} \right)$$
اگر خواستید معادل قطبی یک عدد حقیقی مثبت را بنویسید، آرگومان اصلی آن را برابر صفر قرار دهید.
(ج) بهدست آوردن فرم قطبی این مثال، مشابه مورد حقیقی است. در اینجا نمیتوانیم از فرمول $$\tan \theta = \frac{b}{a}$$ استفاده کنیم، زیرا مخرج کسر صفر خواهد شد. از آنجایی که اعداد موهومی، روی محور $$y$$ قرار دارد، آرگومان اصلی و سایر آرگومانهای آن، بهصورت زیر هستند:
$${\mathop{\rm Arg}\nolimits} z = \frac{\pi }{2} \hspace{0.5in} \arg z = \frac{\pi }{2} + 2\pi n = \pi \left( {\frac{1}{2} + 2n} \right) \hspace{0.25in} n = 0, \pm 1, \pm 2, \ldots$$
همچنین، در این حالت $$r=12$$ و در نتیجه، شکل قطبی عدد مختلط بهصورت زیر است:
$$z = 12\left( {\cos \left( {\frac{\pi }{2}} \right) + i\sin \left( {\frac{\pi }{2}} \right)} \right)$$
فرم نمایی
اکنون که فرم قطبی اعداد مختلط را میشناسیم، میتوانیم فرم نمایی را معرفی کنیم. ابتدا از فرمول اویلر استفاده میکنیم:
$$\begin{equation}{{\bf{e}}^{i\,\theta }} = \cos \theta + i\sin \theta \end{equation}$$
با استفاده از فرمول اویلر میتوانیم فرم قطبی یک عدد مختلط را بهفرم نمایی زیر بنویسیم:
$$z = r{{\bf{e}}^{i\,\theta }}$$
که در آن، $$\theta = \arg z$$ است و مشابه فرم قطبی، بینهایت فرم نمایی برای یک عدد مختلط وجود دارد. همچنین، از آنجایی که هر دو آرگومان یک عدد مختلط، بهاندازه ضریب صحیحی از $$2\pi$$ تفاوت دارند، گاهی فرم قطبی را بهصورت زیر مینویسیم:
$$z = r{{\bf{e}}^{i\,\left( {\theta + 2\pi n} \right)}} \hspace{0.25in} n = 0, \pm 1, \pm 2, \ldots$$
برای بهدست آوردن مقدار $$r$$ میتوانیم از رابطه $$z = \left| z \right|\left( {\cos \theta + i\sin \theta } \right)$$ استفاده کنیم. همچنین میتوانیم مستقیماً آن را بهدست آوریم. اگر اندازه دو طرف تساوی را حساب کنیم و کمی سادهسازی انجام دهیم، داریم:
$$\left| z \right| = \left| {r{{\bf{e}}^{i\,\theta }}} \right| = \left| r \right|\,\left| {{{\bf{e}}^{i\,\theta }}} \right| = \left| r \right|\,\left| {\cos \theta + i\sin \theta } \right| = \sqrt {{r^2} + 0} \,\,\sqrt {{{\cos }^2}\theta + {{\sin }^2}\theta } = r$$
و مشاهده میکنیم: $$r = \left| z \right|$$.
میتوان گفت $$z = r\left( {\cos \theta + i\sin \theta } \right)$$ یک نمایش پارامتری از دایرهای به شعاع $$r$$ است و فرم نمایی یک عدد مختلط، در حقیقت راه دیگری برای نوشتن فرم قطبی بهصورت $$z = r{{\bf{e}}^{i\,\theta }}$$ است که دایره ای به شعاع $$r$$ را نشان میدهد.
اکنون چند مورد از ویژگیهای نمایش نمایی اعداد مختلط را بیان میکنیم.

معکوس اعداد مختلط
عدد مختلط غیرصفر $$z = r{{\bf{e}}^{i\,\theta }}$$ را در نظر بگیرید. معکوس این عدد را میتوان بهصورت زیر نوشت:
$${z^{ - 1}} = {\left( {r{{\bf{e}}^{i\,\theta }}} \right)^{ - 1}} = {r^{ - 1}}{\left( {{{\bf{e}}^{i\,\theta }}} \right)^{ - 1}} = {r^{ - 1}}{{\bf{e}}^{ - i\,\theta }} = \frac{1}{r}{{\bf{e}}^{i\,\left( { - \theta } \right)}}$$
از آنجایی که $$r$$ یک عدد حقیقی غیرصفر است، معکوس آن، $${r^{ - 1}} = \frac{1}{r}$$ خواهد بود. بنابراین، معکوس عدد مختلط بهشکل زیر در میآید:
$$\begin{equation}{z^{ - 1}} = \frac{1}{r}{{\bf{e}}^{i\,\left( { - \theta } \right)}}\end{equation}$$
و فرم قطبی معکوس عدد نیز بهصورت زیر است:
$$\begin{equation}{z^{ - 1}} = \frac{1}{r}\left( {\cos \left( { - \theta } \right) + i\sin \left( { - \theta } \right)} \right)\end{equation}$$
ضرب و تقسیم اعداد مختلط
همچنین میتوانیم فرمولهای ضرب و تقسیم دو عدد مختلط را بهسادگی بیان کنیم. دو عدد مختلط $${z_1} = {r_1}\,{{\bf{e}}^{i\,{\theta _{\,1}}}}$$ و $${z_2} = {r_2}\,{{\bf{e}}^{i\,{\theta _{\,2}}}}$$ را در نظر بگیرید که در آنها، $${\theta _1}$$ یکی از آرگومانهای $$z_1$$ و $$\theta _2$$ یکی از آرگومانهای $$z_2$$ است. برای ضرب و تقسیم این دو عدد، داریم:
$$\begin{align}{z_1}{z_2} &= \left( {{r_1}\,{{\bf{e}}^{i\,{\theta _{\,1}}}}} \right)\left( {{r_2}\,{{\bf{e}}^{i\,{\theta _{\,2}}}}} \right) = {r_1}\,{r_2}{{\bf{e}}^{i\,\left( {{\theta _{\,1}} + {\theta _{\,2}}} \right)}}\\
& \nonumber \\
\frac{{{z_1}}}{{{z_2}}} &= \frac{{{r_1}\,{{\bf{e}}^{i\,{\theta _{\,1}}}}}}{{{r_2}\,{{\bf{e}}^{i\,{\theta _{\,2}}}}}} = \frac{{{r_1}}}{{{r_2}}}{{\bf{e}}^{i\,\left( {{\theta _{\,1}}\, - \,\,{\theta _{\,2}}} \right)}}\end{align}$$
فرم قطبی دو عبارت بالا بهصورت زیر است:
$$\begin{align}{z_1}{z_2} & = {r_1}\,{r_2}\left( {\cos \left( {{\theta _{\,1}} + {\theta _{\,2}}} \right) + i\sin \left( {{\theta _{\,1}} + {\theta _{\,2}}} \right)} \right) \\
& \nonumber \\
\frac{{{z_1}}}{{{z_2}}} & = \frac{{{r_1}}}{{{r_2}}}\left( {\cos \left( {{\theta _{\,1}}\, - \,\,{\theta _{\,2}}} \right) + i\sin \left( {{\theta _{\,1}}\, - \,\,{\theta _{\,2}}} \right)} \right)\end{align}$$
از فرم نمایی ضرب و تقسیم دو عدد مختلط میتوان نتیجه گرفت که در حالت ضرب، آرگومانها با هم جمع و در حالت تقسیم از هم کم میشوند.
$$\begin{align}\arg \left( {{z_1}\,{z_2}} \right) & = \arg {z_1} + \arg {z_2} \\
& \nonumber \\
\arg \left( {\frac{{{z_1}}}{{{z_2}}}} \right) & = \arg {z_1} - \arg {z_2}\end{align}$$
توجه داشته باشید که ممکن است دو معادله اخیر با بهکار بردن آرگومان اصلی $${\rm{Arg }}\,z$$ پاسخ درستی نداشته باشند. برای مثال، دو عدد $${z_1} = i$$ و $${z_2} = - 1$$ را در نظر بگیرید. ضرب دو عدد بهصورت $${z_1}{z_2} = - i$$ خواهد بود و برای آرگومانهای اصلی نیز داریم:
$${\mathop{\rm Arg}\nolimits} \left( i \right) = \frac{\pi }{2} \hspace{0.5in} {\mathop{\rm Arg}\nolimits} \left( { - 1} \right) = \pi \hspace{0.5in} {\mathop{\rm Arg}\nolimits} \left( { - i} \right) = - \frac{\pi }{2}$$
رابطه ضرب دو عدد، آرگومان زیر را به ما خواهد داد که صحیح نیست:
$${\mathop{\rm Arg}\nolimits} \left( i \right) + {\mathop{\rm Arg}\nolimits} \left( { - 1} \right) = \frac{{3\pi }}{2} \ne - \frac{\pi }{2}$$

تساوی اعداد مختلط
در انتها، تساوی دو عدد مختلط را بیان میکنیم. دو عدد مختلط $${z_1} = {r_1}\,{{\bf{e}}^{i\,{\theta _{\,1}}}}$$ و $${z_2} = {r_2}\,{{\bf{e}}^{i\,{\theta _{\,2}}}}$$ را در نظر بگیرید. اگر این دو عدد برابر باشند ($${z_1} = {z_2}$$)، داریم:
$${r_1}\,{{\bf{e}}^{i\,{\theta _{\,1}}}} = {r_2}\,{{\bf{e}}^{i\,{\theta _{\,2}}}}$$
به عبارت بهتر، تساوی $${z_1} = {z_2}$$ برقرار است، اگر و تنها اگر:
$$\begin{equation}{r_1} = {r_2} \hspace{0.25in} {\rm{,}} \hspace{0.25in} {\theta _2} = {\theta _1} + 2\pi k\,\,\,k{\rm{ }}\left( {i.e.\,\,k = 0, \pm 1, \pm 2, \ldots } \right)\end{equation}$$
در آموزشهای بعدی مجله فرادرس، درباره توان و ریشه اعداد مختلط بحث خواهیم کرد.











سلام یک سوال الان iبه توان πچند میشه ؟
بسیار عالی بود – مرسی
سلام سوال این هستش ک نشان دهید z=x+iy در نتیجه ایکس مساو یzبه علاوه ی zبار تقسیم بر ۲ و yمساوی z منهایzبار تقسیم 2i
لطفا پاسخ سوالم بدید ممنون
فوق العاده اید ، ممنون که اینقدر خوب تدریس میکنید و مشکل آدم رو حل میکنید
خداقوت
با سلام خواهشا اثباط قضیه|z1+z2|《|z1|+|z2|
خواهشا قطبی کردنz=_1+1iرو بگید
سلام آرک تانژانت 1- بر روی رادیکال 3 برابر منفی پی شیشم میشه زاویه پنج پی شیشم چجوری باید محاسبه کرد؟
سلام دوست عزیز
منظور از پی، عدد پی(3.14)نیست
منظور، پی رادیان هست
هر پی رادیان برابر ۱۸۰ درجه میباشد
جای پی، ۱۸۰ رو جای گذاری بفرمایید تا جواب رو به درجه بدست بیارید…
سلام یک دوم منهای رادیکال ۳برای قطبی کردنش چجوری حل میشه
کارتان عالی است … با همین فرمون برید جلو…موفق باشید
ممنون از شما عالی بود
عاااالییییی??