فرادرس
خط مماس و قائم بر منحنی — از صفر تا صد
در ادامه مجموعه آموزش‌های ریاضیات مجله فرادرس، در این آموزش به مبحث خط مماس و خط قائم بر منحنی خواهیم پرداخت. ابتدا نحوه به‌دست آوردن معادله خط مماس و قائم بر منحنی را در مختصات کارتزین بیان می‌کنیم. پس از آن، روش محاسبه معادله خطوط مماس و قائم را برای توابع پارامتری و نیز توابع در دستگاه مختصات قطبی بررسی خواهیم کرد.
معادله خط مماس در مختصات کارتزین
فرض کنید تابع $$ y = f\left( x \right) $$ در بازه $$ \left( {a,b} \right) $$ تعریف شده و در $$ {x_0} \in \left( {a,b} \right) $$ پیوسته باشد. در این نقطه (نقطه $$ M$$ در شکل زیر)، مقدار تابع برابر با $$ {y_0} = f\left( {{x_0}} \right) $$ است.
همچنین، فرض کنید متغیر مشتق $$x$$ در $$x _0 $$ دارای نِمُو (افزایش جزئی) $$ \Delta x $$ باشد. نمو متناظر تابع ($$ \Delta y $$) را می‌توان به‌صورت زیر نوشت:
$$ \large \Delta y = f \left( {{ x _ 0 } + \Delta x} \right) – f\left( { { x_ 0 }} \right). $$
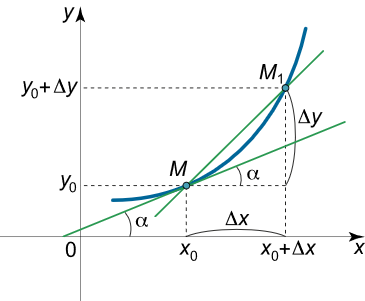
در شکل بالا، نقطه $$M_ 1 $$ در موقعیت $$ \left( {{x_0} + \Delta x,{y_0} + \Delta y} \right) $$ قرار دارد. پاره‌خط $$MM_1$$ را رسم می‌کنیم که معادله آن به‌صورت زیر است:
$$ \large y – { y _ 0 } = k\left( { x – { x _ 0} } \right) $$
که در آن، $$k$$ شیب برحسب نمو $$ \Delta x $$ بوده و برابر است با:
$$ \large k = k\left( {\Delta x} \right) = \frac{{\Delta y}}{{\Delta x}}. $$
وقتی $$ \Delta x $$ کاهش پیدا کند، نقطه $$M_1$$ به‌سمت نقطه $$M$$ حرکت می‌کند: $$ {M_1} \to M $$. در شرایط حدیِ $$ \Delta x \to 0 $$، فاصله بین نقاط $$M$$ و $$M_1 $$ به صفر میل می‌کند. با توجه به شرط پیوستگی تابع $$ f( x) $$ در نقطه $$ x_0 $$، داریم:
$$ \large { \lim \limits_ { \Delta x \to 0} \Delta y = 0,\;\;}\Rightarrow
{\lim\limits _ { \Delta x \to 0} \left| { M {M _ 1 } } \right| }
= {\lim\limits_{\Delta x \to 0} \sqrt {{{\left( {\Delta x} \right)} ^ 2 } + {{\left( {\Delta y} \right) } ^ 2 } } = 0 . } $$
وضعیت حدی پاره‌خط $$MM_1$$، خط مماس بر منحنی تابع $$ y = f (x ) $$ در نقطه $$M $$ نامیده می‌شود.
دو نوع خط مماس وجود دارد: «خط مماس مایل» (Oblique Tangent) و «خط مماس قائم» (Vertical Tangent).
تعریف ۱
اگر حد کران‌دار و محدود $$ \lim\limits_{\Delta x \to 0} k\left( {\Delta x} \right) = {k_0} $$ را داشته باشیم، آن‌گاه معادله خط مستقیم به‌صورت زیر است:
$$ \large y – {y _ 0 } = k \left( { x – { x _ 0 } } \right) $$
که مماس مایل منحنی $$ y = f ( x ) $$ در نقطه $$ ( x _ 0 , y _ 0 ) $$ نامیده می‌شود.
تعریف ۲
اگر $$ \Delta x \to 0 $$، مقدار $$k$$ بی‌نهایت شود، یعنی $$ \lim\limits_{\Delta x \to 0} k\left( {\Delta x} \right) = \pm \infty $$، آن‌گاه معادله خط به‌صورت زیر خواهد بود:
$$ \large x = {x_0} $$
که خط مماس قائم منحنی تابع $$ f( x ) $$ در نقطه $$ \left( {{x_0},{y_0}} \right) $$ نامیده می‌شود.
لازم است بدانیم:
$$ \large {{k_0} = \lim \limits _ {\Delta x \to 0} k\left( {\Delta x} \right) }
= { \lim \limits _ { \Delta x \to 0} \frac{{\Delta y } } { {\Delta x } } }
= { f’\left( { { x _ 0 } } \right)} $$
یعنی شیب خط مماس، برابر با مشتق تابع $$ f(x)$$ در نقطه مماس $$ x_ 0 $$ است. بنابراین، معادله مماس مایل را می‌توان به‌فرم زیر نوشت:
$$ \large { y – { y _ 0 } = f’\left( { { x _ 0 } } \right)\left( {x – { x _ 0}} \right)\;\;}$$
یا
$$ \large { y = f’ \left( {{x_0}} \right)\left( {x – { x _ 0 } } \right) + f\left( { { x _ 0 } } \right)} $$
از آن‌جایی که شیب خط، برابر با تانژانت زاویه $$ \alpha $$ (زاویه بین خط و جهت مثبت محور $$x$$) است، تساوی زیر را داریم:
$$ \large k = \tan \alpha = f’ \left( { { x _ 0}} \right) $$
معادله خط قائم در مختصات کارتزین
خط راست عمود بر خط مماس بر منحنی که آن را در نقطه تماس $$ \left( {{x_0},{y_0}} \right) $$ قطع می‌کند، «خط قائم» یا خط عمود یا خط نرمال (Normal Line) بر منحنی تابع $$ y = f (x) $$ در این نقطه نامیده می‌شود.
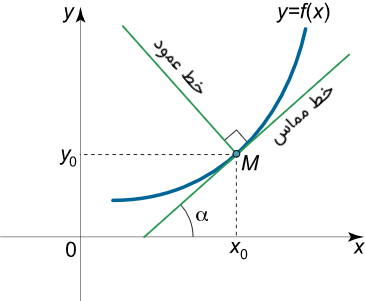
از هندسه می‌دانیم که ضرب شیب‌های دو خط عمود بر هم برابر با $$ -1 $$ است. بنابراین، با داشتن معادله خط مماس در نقطه $$ \left( {{x_0},{y_0}} \right) $$، یعنی:
$$ \large y – { y _ 0 } = f ’ \left( { { x _ 0 } } \right)\left( {x – { x _ 0 } } \right), $$
می‌توانیم معادله خط قائم را به‌سادگی بنویسیم:
$$ \large y – { y _ 0 } = – \frac { 1 } { { f ’ \left( { { x _ 0 } } \right) } } \left( { x – { x _ 0 } } \right ) . $$
معادله خط مماس و قائم بر منحنی در فرم پارامتری
فرض کنید منحنی یک حرکت در صفحه به‌فرم پارامتری زیر داده شده است:
$$ \large {x = x \left( t \right),}\;\;\;\kern-0.3pt{ y = y \left( t \right) . } $$
آن‌گاه شیب خط مماس بر نقطه $$ \left( {{x_0},{y_0}} \right) $$ را می‌توان با استفاده از قاعده مشتق توابع پارامتری به‌صورت زیر نوشت:
$$ \large k = \tan \alpha = \frac{{{y’_ t } }} { {{ x’ _ t } }} . $$
بنابراین، معادله خط مماس به‌فرم زیر خواهد بود:
$$ \large {y – { y _ 0 } = \frac{ { { y ’_ t} } }{ {{ x ’_ t} } } \left( { x – { x_ 0} } \right)}$$
یا
$$ \large \frac{{x – { x _ 0} }} {{ { x’ _t } } } = \frac{ { y – { y _0 }} } { {{ y’ _t } } } $$
بر همین اساس، معادله خط قائم به‌صورت زیر است:
$$ \large { y – { y _ 0} = – \frac { { { x ’ _ t } } } { { { y ’ _ t } } } \left( { x – { x _ 0 } } \right)} $$
یا
$$ \large {\;\;\;\kern-0.3pt\frac{{x – {x _ 0} } } {{ { y ’ _ t } } } = – \frac{{y – { y _ 0 } } }{ { {x ’ _ t } } } . } $$
معادله خط مماس و قائم در مختصات قطبی
فرض کنید منحنی با معادله قطبی $$ r = f\left( \theta \right) $$ بیان شده باشد که براساس طول بردار شعاعی $$r$$ و زاویه قطبی $$ \theta $$ است. در مختصات کارتزین، این منحنی به‌صورت زیر بیان می‌شود:
$$ \large \left\{ \begin {array} {l}
x = r \cos \theta = f\left( \theta \right) \cos \theta \\
y = r \sin \theta = f\left( \theta \right) \sin\theta
\end{array} \right.. $$
بنابراین، معادله پارامتری منحنی را می‌نویسیم که در آن، زاویه $$ \theta $$ نقش یک پارامتر را ایفا می‌کند. در ادامه، توصیف شیب خط مماس بر منحنی را در نقطه $$ \left( {{x_0},{y_0}} \right) $$ به‌دست می‌آوریم:
$$ \large {k = \tan \theta = \frac { { { y ’_\theta } } }{{ {x ’ _\theta }}} }
= {\frac { { { { \left( {r\sin \theta } \right) } ^ \prime }}}{ { {{\left( {r\cos \theta } \right) } ^ \prime }}} }
= { \frac { {{ r ’_\theta }\sin \theta + r \cos \theta }} { { { r ’ _ \theta }\cos\theta – r\sin \theta }}.} $$
در نتیجه، معادله مربوط به خط مماس و خط قائم به‌ترتیب، به‌صورت زیر خواهد بود:
$$ \large { y – { y _ 0 } = \frac { { { y’_\theta } }} { { { x ’_ \theta }}}\left( { x – { x _ 0 } } \right)} $$
$$ \large { y – { y _ 0 } = - \frac { { { x ’ _ \theta } } }{ { {y ’ _ \theta } } } \left( { x – { x _ 0 } } \right) } . $$
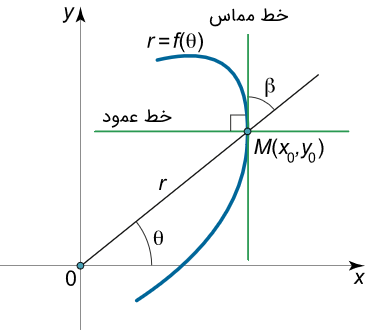
منحنی‌ها را می‌توان مستقیماً در مختصات قطبی و بدون تبدیل به دستگاه مختصات کارتزین بررسی کرد. در این حالت، به‌جای زاویه $$ \theta $$ نسبت به محور قطبی (یعنی جهت مثبت محور $$ x $$)، ساده‌تر است که زاویه $$ \beta $$ را نسبت به خط شامل بردار شعاعی $$r$$ در نظر بگیریم.
تانژانت زاویه $$ \beta $$ را می‌توان با استفاده از فرمول زیر به‌دست آورد:
$$ \large \tan \beta = \frac { r } { { { r ’ _ \theta } } } . $$
مثال‌ها
در ادامه، چند مثال را حل می‌کنیم.
مثال ۱
معادله خط مماس بر منحنی تابع $$ y = x\sqrt {x – 1} $$ را در نقطه $$ x= 2 $$به‌دست آورید.
حل: ابتدا مشتق تابع را محاسبه می‌کنیم:
$$ \large { y ’ \left( x \right) = {\left( { x \sqrt { x – 1 } } \right) ^ \prime } }
= { x ’ \sqrt { x – 1 } + x { \left( {\sqrt { x – 1 } } \right) ^ \prime } } \\ \large
= {\sqrt { x – 1 } + \frac { x } { { 2 \sqrt { x – 1 } } } }
= { \frac { { 2 \left( { x – 1 } \right) + x } } { { 2 \sqrt { x – 1 } } } }
= { \frac { { 3 x – 2 } }{ { 2 \sqrt { x – 1 } } } .} $$
در نقطه $$ x= 2$$، مشتق برابر است با:
$$ \large y ’ \left( 2 \right) = \frac { { 3 \cdot 2 – 2 } } { { 2 \sqrt { 2 – 1 } } } = 2 . $$
مقدار خود تابع نیز در این نقطه به‌صورت زیر است:
$$ \large y\left( 2 \right) = 2 \cdot 1 = 2. $$
در نهایت، معادله خط مماس در این نقطه، به‌شکل زیر به‌دست می‌آید:
$$ \large {y – {y_0} = y’\left( {{x_0}} \right)\left( {x – {x_0}} \right),\;\;}\Rightarrow
{ y – 2 = 2\left( {x – 2} \right),\;\;} \\ \large \Rightarrow
{ y – 2 = 2x – 4,\;\;}\Rightarrow
{ y = 2 x – 2.} $$
مثال ۲
سهمی $$ y = 2{x^2} $$ را در نظر بگیرید. پاره‌خطی بین دو نقطه $$ x = - 1 $$ و $$ x= 2 $$ از این منحنی رسم شده است. خط مماس بر منحنی را که موازی این پاره‌خط است، پیدا کنید.
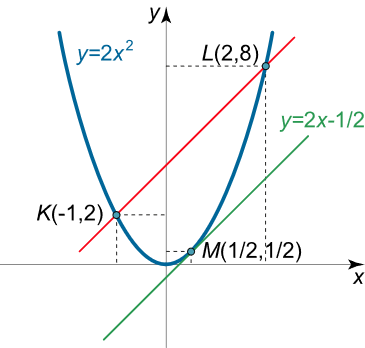
حل: ابتدا مقدار $$ y $$ را برای نقاط $$x$$ داده‌شده پاره‌خط $$ KL$$ محاسبه می‌کنیم:
$$ \large { y \left( { – 1 } \right) = 2 \cdot {\left( { – 1 } \right) ^ 2 } = 2;}\;\;\;\kern-0.3pt
{ y \left( 2 \right) = 2 \cdot { 2 ^ 2 } = 8 . } $$
معادله پاره‌خط $$ KL $$ را به‌صورت زیر می‌نویسیم:
$$ \large {\frac { { y – { y _ K } }} { { { y _ L } – { y _ K } } } = \frac{ { x – { x _ K }} } {{ {x _ L } – { x_K }} } ,\;\;}\Rightarrow
{\frac { { y – 2 } } { { 8 – 2 } } = \frac { { x – \left( { – 1} \right) }} { { 2 – \left( { – 1 } \right) } },\;\;} \\ \large \Rightarrow
{\frac { { y – 2} } { 6 } = \frac { { x + 1 } }{ 3 } ,\;\;}\Rightarrow
{ y – 2 = 2 \left( { x + 1 } \right),\;\;}\Rightarrow
{ y = 2 x + 4 , } $$
که در آن، $$k=2 $$ است. شیب خط مماس نیز برابر با مقدار $$ k= 2 $$ است.
اکنون مختصات $$x$$ نقطه مماس را با شرایط $$ y’\left( x \right) = k $$ پیدا می‌کنیم:
$$ \large { y ’ \left( x \right) = k ,\;\;} \Rightarrow
{ { \left( { 2 { x ^ 2 } } \right) ^ \prime } = 2,\;\;}\Rightarrow
{ 4 x = 2 ,\;\;}\Rightarrow
{ x = \frac{1}{2}.} $$
مقدار $$ y $$ نیز در نقطه $$M $$ برابر است با:
$$ \large { y _ M } = 2 \cdot {\left( {\frac{1}{2}} \right) ^ 2 } = \frac { 1} {2 } . $$
بنابراین، نقطه مماس $$ M $$ در نقطه $$ \left( {\large\frac{1}{2}\normalsize,\large\frac{1}{2}\normalsize} \right) $$ واقع شده است. در نتیجه می‌توانیم معادله خط مماس بر منحنی را به‌صورت زیر بنویسیم:
$$ \large { y – { y _ M } = k \left( { x – { x _ M } } \right),\;\;}\Rightarrow
{ y – \frac {1 } { 2} = 2\left( {x – \frac { 1} { 2 }} \right),\;\;} \\ \large \Rightarrow
{ y – \frac {1 } {2 } = 2 x – 1,\;\;}\Rightarrow
{ y = 2 x – \frac { 1} {2 } . } $$
مثال ۳
مساحت مثلثی را تعیین کنید که با خط مماس بر منحنی تابع $$ y = 3 – {x^2} $$ در نقطه $$ \left( {1,2} \right) $$ و محورهای مختصات تشکیل شده است.
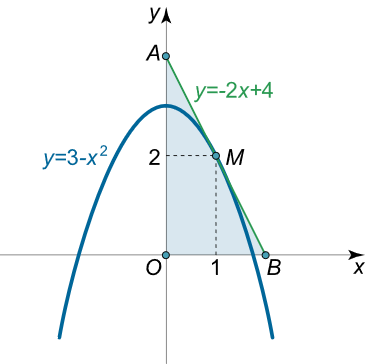
حل: ابتدا معادله خط مماس را به‌دست می‌آوریم. محل برخورد خط مماس و منحنی، نقطه زیر است:
$$ \large { f ’ \left( x \right) = \left( {3 – { x ^ 2 } } \right) = – 2x;\;\;}\Rightarrow
{ f ’ \left( 1 \right) = – 2 , } $$
در نتیجه، معادله خط مماس را به‌صورت زیر می‌نویسیم:
$$ \large {y – { y _ M } = f ’ \left( { { x _ M}} \right)\left( {x – {x_M}} \right),\;\;} \\ \large \Rightarrow
{y – 2 = – 2 \left( {x – 1} \right),\;\;}\Rightarrow
{y = – 2 x + 4 . } $$
معادله را به‌فرم زیر می‌توان نوشت:
$$ \large { y = – 2 x + 4,\;\;}\Rightarrow
{ y + 2x = 4,\;\;}\\ \large \Rightarrow
{\frac { y } { 4 } + \frac { {2 x }} { 4} = 1,\;\;}\Rightarrow
{\frac { y} { 4 } + \frac {x } { 2} = 1.} $$
طول پاره‌خط‌های $$OA$$ و $$ O B $$ به‌ترتیب $$ 4 $$ و $$ 2 $$ است. بنابراین، مساحت $$ OAB $$ به‌صورت زیر به‌دست می‌آید:
$$ \large S = \frac { { \left| { O A } \right| \cdot \left| {O B } \right| }} { 2 } = \frac { { 4 \cdot 2 } } { 2 } = 4 . $$
مثال ۴
زاویه بین خط مماس بر دل‌گون $$ r = a\left( {1 + \cos \theta } \right) $$ و بردار شعاعی را در نقطه مماس به‌دست آورید.
حل: زاویه مورد نظر را با فرمول زیر محاسبه می‌کنیم:
$$ \large \tan \omega = \frac { r } { { { r ’_ \theta } } } . $$
با جایگذاری $$ r $$ در فرمول اخیر داریم:
$$ \large { { r ’ _ \theta } = {\left[ { a \left( { 1 + \cos \theta } \right)} \right] ^ \prime } }
= { – a \sin \theta . } $$
در نتیجه، مقدار تانژانت برابر است با:
$$ \large \require {cancel}
{\tan \omega = \frac { { a \left( { 1 + \cos \theta } \right) } } { { \left( { – a \sin \theta } \right) } } }
= { – \frac { { 1 + \cos \theta } } { { \sin \theta } } } \\ \large
= { – \frac { { \cancel { 2 } { { \cos } ^ { \cancel { 2 } } } \frac{\theta } { 2 } } } { { \cancel { 2 } \sin \frac { \theta } { 2 } \cancel { \cos \frac { \theta } { 2 } } } } }
= { – \cot \frac{\theta } { 2 } }
= { \tan \left( { \frac {\theta } { 2 } + \frac { \pi } { 2 } } \right) . } $$
بنابراین، زاویه بین خط مماس و بردار شعاعی، به‌صورت زیر است:
$$ \large \omega = \frac { \theta } { 2 } + \frac { \pi } { 2 } . $$
مثال ۵
معادله خط عمود بر بیضی $$ \frac{{{x^2}}}{4} + \frac{{{y^2}}}{1} = 1 $$ را در نقطه $$ \left( {1,{\large\frac{{\sqrt 3 }}{2}\normalsize}} \right) $$ به‌دست آورید.
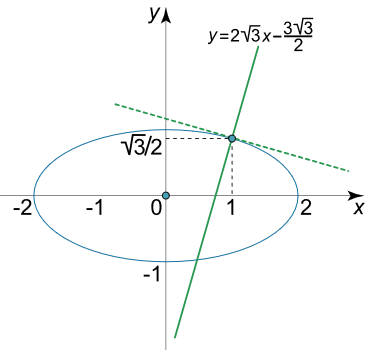
حل: ابتدا مقدار $$ y’\left( x \right) $$ را با استفاده از مشتق‌گیری ضمنی به‌دست می‌آوریم:
$$ \large { { \left( { \frac { { { x ^ 2 } } } { 4 } + \frac { { { y ^ 2 } } } { 1 } } \right) ^ \prime } = 1′,\;\;}\\ \large \Rightarrow
{ \frac { { 2 x } } { 4 } + 2 y y ’ = 0,\;\;} \Rightarrow
{ 4 y y ’ = – x ,\;\;}\Rightarrow
{ y ’ = – \frac { x } { { 4 y } } . } $$
مشتق در نقطه مماس برابر است با:
$$ \large { y ’ \left( { { x _ 0 } , { y _ 0 } } \right) = y ’ \left( { 1 , \frac { { \sqrt 3 } } { 2 } } \right) }
= { – \frac { 1 } { { \frac { { 4 \sqrt 3 } } { 2 } } } }
= { – \frac { 1 } { { 2 \sqrt 3 } } . } $$
در نتیجه، معادله خط قائم به‌صورت زیر به‌دست می‌آید:
$$ \large { y – { y _ 0 } = – \frac { 1 } { { y ’ \left( { { x _ 0 } , { y _ 0 } } \right) } } \left( { x – { x _ 0 } } \right),\;\;}\Rightarrow
{ y – \frac { { \sqrt 3 } } { 2 } = – \frac { 1 } { { \left( { – \frac { 1 } { { 2 \sqrt 3 } } } \right) } } \left( { x – 1 } \right),\;\;} \\ \large\Rightarrow
{ y – \frac { { \sqrt 3 } } { 2 } = 2 \sqrt 3 x – 2\sqrt 3 ,\;\;}\Rightarrow
{ y = 2 \sqrt 3 x – 2 \sqrt 3 + \frac { { \sqrt 3 } }{ 2 },\;\; } \\ \large \Rightarrow
{ y = 2 \sqrt 3 x – \frac { { 3 \sqrt 3 } } { 2 } } \approx { 3,46x – 2,60.} $$
مثال ۶
معادله خطوط مماس و قائم بر ستاره‌گون $$ x = a\,{\cos ^3}t,y = a\,{\sin ^3}t $$ را در نقطه $$ t = \large\frac{\pi }{4}\normalsize $$ به‌دست آورید.
حل: ابتدا مشتقات تابع پارامتری را محاسبه می‌کنیم:
$$ \large { { x ’ _ t } = { \left( { a \, { { \cos } ^ 3 } t } \right) ^ \prime } = – 3 a \,{ \cos ^ 2 } t \sin t; } \\ \large
{ { y ’ _ t } = { \left ( { a \, { { \sin } ^ 3 } t } \right) ^ \prime } = 3 a \,{ \sin ^ 2 } t \cos t . } $$
در نتیجه، داریم:
$$ \large { { y ’ _ x } = \frac { { { y ’ _ t } } } { { { x ’ _ t } } } }
= { \frac { { 3 a\,{ { \sin } ^ 2 } t \cos t}}{{\left( { – 3a\,{{\cos } ^ 2 } t \sin t } \right)}} }
= { – \frac { { \sin t } } { { \cos t } } }
= { – \tan t . } $$
حاصل را می‌توانیم به‌صورت زیر بنویسیم:
$$ \large – \tan t = \tan \left( {\pi – t} \right). $$
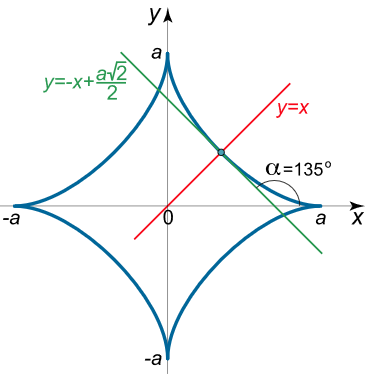
از آن‌جایی که $$ \tan \alpha = {y’_x} = \tan \left( {\pi – t} \right) $$، زاویه $$ \alpha $$ برابر است با:
$$ \large { \alpha = \pi – t }
= { \pi – \frac { \pi } { 4 } }
= { \frac { { 3 \pi } } { 4 } = 135 ^ { \circ } . } $$
بنابراین، مشتق و در نتیجه شیب خط مماس بر ستاره‌گون، برابر است با:
$$ \large { y ’ _ x } \left( { \frac { \pi } { 4 } } \right) = \tan \frac { { 3 \pi } } { 4 } = – 1 . $$
مختصات نقطه مماس در دستگاه کارتزین به‌صورت زیر محاسبه می‌شود:
$$ \large { { x _ 0 } = x \left( { \frac { \pi } { 4 } } \right) }
= { a\ , { \cos ^ 3 } \frac { \pi } { 4 } }
= { a { \left( { \frac { { \sqrt 2 } } { 2 } } \right) ^ 3 } }
= { \frac { { a \sqrt 2 } } { 4 } , } $$
$$ \large { { y _ 0 } = y \left( { \frac { \pi } { 4 } } \right) }
= { a\ , { \sin ^ 3 } \frac { \pi } { 4 } }
= { a { \left( { \frac { { \sqrt 2 } } { 2 } } \right) ^ 3 } }
= { \frac { { a \sqrt 2 } } { 4 } . } $$
اکنون می‌توان معادله خط مماس را نوشت:
$$ \large { y – { y _ 0 } = { y ’ _ x }\left( { { x _ 0 } } \right)\left( { x – { x _ 0 } } \right),\;\;}\Rightarrow
{ y – \frac { { a \sqrt 2 } } { 4 } = – 1 \left( { x – \frac { { a \sqrt 2 } } { 4 } } \right),\;\;} \\ \large \Rightarrow
{ y – \frac { { a \sqrt 2 } } { 4 } = – x + \frac { { a \sqrt 2 } } { 4 },\;\;}\Rightarrow
{ y = – x + \frac { { a \sqrt 2 } } { 2 } } $$
و معادله خط عمود بر آن برابر است با:
$$ \large { y – { y _ 0 } = – \frac { 1 } { { { { y ’ } _ x }\left( { { x _ 0 } } \right) } } \left( { x – { x _ 0 } } \right),\;\;} \\ \large \Rightarrow
{ y – \frac { { a \sqrt 2 } } { 4 } = – \frac { 1 } { { \left( { – 1 } \right) } } \left( { x – \frac { { a \sqrt 2 } } { 4 } } \right),\;\;} \\ \large \Rightarrow{y – \cancel{\frac{{a\sqrt 2 }}{ 4 } } = x – \cancel{\frac{{a\sqrt 2 } } { 4}},\;\;}\Rightarrow{y = x.} $$
معرفی فیلم آموزش ریاضی پایه دانشگاهی
یکی از آموزش‌هایی که برای آشنایی بیشتر با مبحث اتحاد و تجزیه می‌توانید به آن مراجعه کنید، آموزش ریاضی پایه دانشگاهی است. این آموزش که مدت آن ۱۲ ساعت و ۴۶ دقیقه است، در قالب ۱۰ درس تهیه شده است.
در درس اول، مجموعه‌ها، مجموعه اعداد، توان، ب.م.م و ک.م.م معرفی شده‌اند. موضوعات درس دوم، چندجمله‌ای‌ها و اتحاد و تجزیه است. در درس سوم، نامساوی‌ها، نامعادلات، طول پاره‌خط، ضریب زاویه و معادله خط مورد بحث قرار گرفته‌اند. مثلثات موضوع مهم درس چهارم است. تصاعد حسابی و هندسی در درس پنجم بررسی شده‌اند. تابع و دامنه و برد آن موضوعات مهم درس ششم هستند. در درس هفتم، تساوی دو تابع، اعمال جبری روی تابع و ترکیب توابع ارائه شده‌اند. در درس هشتم به توابع زوج و فرد، تابع یک به یک و تابع وارون پرداخته شده است. انواع توابع از قبیل تابع ثابت، تابع همانی، تابع علامت، تابع قدر مطلق و تابع جزء صحیح موضوع درس نهم هستند. در نهایت، در درس دهم توابع نمایی و لگاریتمی مورد بحث قرار گرفته‌اند.
- برای مشاهده فیلم آموزش ریاضی پایه دانشگاهی + اینجا کلیک کنید.
معرفی فیلم آموزش ریاضی پایه (مرور و حل تست کنکور ارشد)
فیلم آموزش ریاضی پایه (مرور و حل تست کنکور ارشد) در ۵ ساعت و ۱۶ دقیقه و در قالب ۴ درس تهیه شده است. درس یکم این آموزش درباره مجموعه‌ها، چندجمله‌ای‌ها، اتحاد و تجزیه، نامساوی و نامعادلات است. در درس دوم، معادله درجه 2 مورد بررسی قرار گرفته است. موضوع درس سوم مثلثات است. در نهایت، در درس چهارم به تابع، دامنه و برد آن، تساوی دو تابع، اعمال جبری روی تابع، ترکیب توابع، توابع زوج و فرد، توابع یک به یک، وارون تابع، تابع ثابت، تابع همانی، تابع علامت، تابع قدر مطلق، تابع جزء صحیح، تابع نمایی و تابع لگاریتمی پرداخته شده است.
- برای مشاهده فیلم آموزش ریاضی پایه (مرور و حل تست کنکور ارشد) + اینجا کلیک کنید.
اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:
^^
