مشتق لگاریتم و تابع نمایی – از صفر تا صد

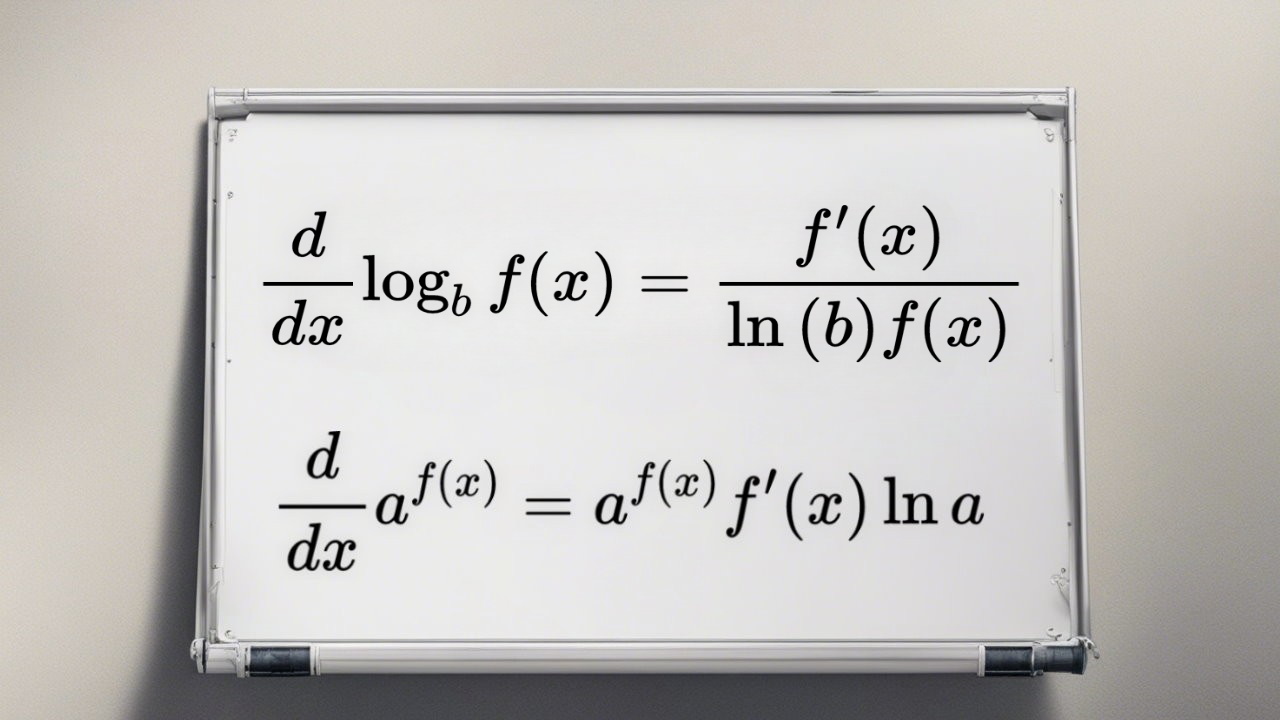
در راستای معرفی جامع مفهوم مشتق، در این مطلب قصد داریم تا مشتق لگاریتم و توابع نمایی را توضیح دهیم. توجه داشته باشید که بسیاری از توابع مورد استفاده به‌منظور مدل‌سازی پدیده‌های فیزیکی به صورت نمایی یا لگاریتمی هستند. برای نمونه شکل کابل‌های انتقال توان الکتریکی به صورت نمایی است.

توابع نمایی

در حالت کلی به تابعی نمایی گفته می‌شود که در آن عدد به توان یک متغیر رسیده باشد. در ابتدا قصد داریم تا مشتق تابعی به صورت زیر را توضیح دهیم.

$$f \left( x \right) = { a ^ x }$$

پیش‌تر در مطلب روش‌های مشتق‌گیری روشی تحت عنوان قانون توانی را توضیح دادیم. در این قانون از تابعی که به توان عددی ثابت رسیده بود، مشتق گرفته می‌شد. اما توجه داشته باشید که در این‌جا نمی‌توان از این قانون استفاده کرد. دلیل این امر متغیر بودن توان تابع است. در نتیجه به‌ منظور بدست آوردن مشتق تابع نمایی از تعریف مشتق استفاده می‌کنیم. با به‌کارگیری تعریف پایه‌ای مشتق داریم:

$$\begin{align*} f ^{\prime}\left( x \right) & = \mathop {\lim }\limits _{h \to 0} \frac{{f\left( { x + h} \right) - f\left( x \right)}}{h}\\ & = \mathop {\lim }\limits _ {h \to 0} \frac{ { { a ^ { x + h}} - {a ^ x }}}{ h }\\ & = \mathop {\lim }\limits_{h \to 0} \frac{{{a^x}{a^h} - {a^x}}}{ h }\\ & = \mathop {\lim }\limits_{h \to 0} \frac{ { { a ^ x }\left( {{a^h} - 1} \right)}}{ h }\end{align*}$$

بدیهی است که در رابطه فوق $${ a ^ x }$$ مستقل از h بوده و می‌توان آن را بیرون کشید.

$$f ^{\prime} \left( x \right) = { a ^ x } \mathop { \lim } \limits_{ h \to 0} \frac{ { { a ^ h } - 1}}{ h }$$

حاصل حد $$f ^{\prime} \left( x \right) = \mathop { \lim } \limits_{ h \to 0} \frac{ { { a ^ h } - 1}}{ h }$$ دقیقا نشان دهنده مشتق تابع در x=0 است. با توجه این توصیفات، مشتق تابع (f(x برابر می‌شود با:

$$f ^{\prime} \left ( x \right) = f ^{\prime} \left( 0 \right) { a ^ x }$$

رابطه فوق مناسب نیست،‌ چرا که ما به دنبال مشتق یک تابع در قالب یک تابع هستیم! تنها یک مقدار از a وجود دارد که با مفاهیم آن آشنا هستیم. این عدد e یا همان عدد نپر است؛ چرا که راه‌های متفاوتی به‌منظور تعریف عدد e وجود دارد. سه مورد از تعریف‌های مذکور در ادامه آمده‌اند.

• $$\displaystyle { \bf { e } } = \mathop { \lim }\limits _ { n \to \infty } { \left( {1 + \frac{1}{ n } } \right) ^ n }$$
• e عددی ویژه و مثبت است که در حاصل حد $$\mathop { \lim }\limits _ { h \to 0} \frac{{{{\bf{ e } } ^ h } - 1 } } { h } = 1$$ صدق می‌کند.
• عدد e را می‌توان برابر با سری $$\displaystyle { \bf { e } } = \sum \limits _ { n = 0} ^ \infty {\frac{ 1 } { { n ! } } }$$ در نظر گرفت.

مناسب‌ترین تعریف برای ما مورد دوم است. چرا که این مورد دقیقا عبارتی است که با آن کار می‌کنیم. این تعریف نتایج زیر را در پی دارد.

برای یک تابع نمایی طبیعی که به صورت $$f \left ( x \right ) = { { \bf { e } } ^ x }$$ است، مشتق تابع در نقطه x=0 برابر با $$f ^{\prime} \left( 0 \right) = \mathop { \lim } \limits _ { h \to 0} \frac{{{{\bf{ e } } ^ h} - 1}} { h } = 1$$ است. بنابراین مشتق تابع نمایی برابر با تابع زیر بدست می‌آید.

$$f \left( x \right) = {{\bf{ e } } ^ x }\hspace{0.5in} \Rightarrow \hspace{0.5in}f^{\prime}\left( x \right ) = { { \bf { e } } ^ x }$$

به‌ منظور بدست آوردن مشتق تابع $$f\left( x \right) = {a^x}$$ می‌توان آن را به ترتیب زیر به شکلی نمایی نوشت. در این صورت خواهیم داشت:

\begin{align*}f\left( x \right) & = { a ^ x }\\ & = {\left( a \right) ^ x }\\ & = {\left( {{{\bf{ e }}^{\ln a } } } \right) ^ x }\\ & = {{\bf { e } } ^ {\left( {\ln a } \right) x } }\\ & = {{\bf{ e }}^{ x\,\,\ln a } } \end{align*}

با استفاده از قانون مشتق‌گیری توانی، مشتق تابع $$e ^ { x \ln a }$$ برابر با تابع زیر بدست می‌آید.

$$f ^{\prime} \left( x \right) = { {\bf{ e } } ^ { x\,\,\ln a}}\left( {\ln a } \right)$$

از طرفی $$e ^ { x \ln a }$$ را می‌توان برابر با $$a ^ { x }$$ نوشت. در این صورت رابطه فوق نیز به‌صورت زیر به دست می‌آید.

$$f ^{\prime} \left( x \right ) = { a ^ x } \ln \left ( a \right)$$

بنابراین نهایتا می‌توان مشتق تابع نمایی را به صورت زیر بیان کرد:

$$f\left( x \right) = {a ^ x } \hspace {0.5in } \Rightarrow \hspace{0.5in}f^{\prime}\left ( x \right) = {a ^ x} \ln \left( a \right)$$

اثبات مشتق تابع $$e ^ { x \ln a }$$

به منظور مشتق تابع $$e ^ { x \ln a }$$، تغییر متغیر زیر را در نظر بگیرید:

$$e ^ x = u$$

بنابراین:

$$e ^ { x \ln a } = u ^ { \ln a }$$

اکنون، از تغییر دو طرف رابطه $$e ^ x = u$$ مشتق می‌گیریم:

$$\frac { d } { d x } e ^ x = \frac { d } { d x } u$$

می‌دانیم که مشتق $$e ^ x$$ بر حسب $$x$$ برابر با خودش است. به این ترتیب، داریم:

$$e ^ x = \frac { d u } { d x }$$

رابطه به دست آمده را بر حسب $$d x$$ بازنویسی می‌کنیم:

$$d x = \frac { d u } { e ^ x }$$

با توجه به این رابطه و بر اساس تغییر متغیرهای فرضی، به سراغ مشتق $$e ^ { x \ln a }$$ می‌رویم. این مشتق به صورت زیر نوشته می‌شود:

$$\frac { d } { d x } e ^ { x \ln a } = \frac { d } { d x } u ^ { \ln a }$$

$$d x = d u e ^ x$$ را در سمت راست معادله بالا قرار می‌دهیم:

$$\frac { d } { d x } e ^ { x \ln a } = \frac { d } { \frac { d u } { e ^ x } } u ^ { \ln a }$$

$$\frac { d } { d x } e ^ { x \ln a } = e ^ x \frac { d } { d u } u ^ { \ln a }$$

بر اساس قانون مشتق عبارات توانی، داریم:

$$\frac { d } { d u } u ^ { \ln a } = \ln a u ^ { \ln a - 1 } = \frac { \ln a u ^ { \ln a }} { u }$$

تغییر متغیرها را درون مشتق بالا جایگذاری می‌کنیم:

$$\frac { d } { d u } u ^ { \ln a } = \frac { \ln a e ^ { x \ln a }} { e ^ x }$$

در نتیجه:

$$\frac { d } { d x } e ^ { x \ln a } = e ^ x \frac { \ln a e ^ { x \ln a }} { e ^ x }$$

$$\frac { d } { d x } e ^ { x \ln a } = \ln a e ^ { x \ln a }$$

تابع لگاریتمی

تابع لگاریتمی عکس تابع نمایی است. بنابراین می‌توان به‌ منظور مشتق‌گیری از آن، از مفهوم تابع معکوس استفاده کرد.

فیلم آموزش ریاضی پایه دانشگاهی – جامع و کاربردی + گواهینامه در فرادرس

کلیک کنید

اگر دو تابع $$f ( x )$$ و $$g ( x )$$ معکوس یکدیگر باشند، در این صورت رابطه‌ای به صورت زیر را می‌توان بین آن‌ها بیان کرد:

$$g ^{\prime} \left( x \right ) = \frac{ 1 } { { f ^{\prime}\left( { g\left( x \right)} \right)}}$$

حال چگونه می‌توان از قانون بیان شده در بالا استفاده کرد. در این مرحله لازم است بگوییم که معکوس تابع $$f \left( x \right ) = { {\bf { e } } ^ x }$$ برابر با $$g \left( x \right) = \ln x$$ است. در این صورت با استفاده از قانون مشتق معکوسِ بیان شده در بالا، داریم:

$$g ^{\prime} \left( x \right) = \frac{1}{{f^{\prime}\left( { g \left( x \right)} \right)}} = \frac { 1 }{{{{\bf{ e }}^{g\left( x \right)}}}} = \frac{ 1 }{{{{ \bf{ e }} ^ {\ln x} } } } = \frac{1}{ x }$$

البته به صورت دقیق‌تر، حاصل مشتق‌گیری تابع لگاریتمی را بایستی به صورت زیر بیان کرد:

$$\frac { d } { { d x } } \left ( { \ln x } \right ) = \frac { 1 } { x } \hspace { 0.5in } x > 0$$

هم‌چنین می‌توان متغیر درون تابع را همانند زیر به صورت قدر مطلق در نظر گرفت.

$$\frac{ d } {{ d x } }\left( { \ln \left| x \right|} \right) = \frac{ 1 } { x }\hspace{0.5in} x \ne 0$$

با توجه به یافته شدن مشتق تابع $$\ln x$$، در مرحله بعد می‌توان مشتق تابع $$\log x$$ را نیز بدست آورد. در حقیقت در این حالت بایستی لگاریتم را بر حسب لگاریتم در مبنای e نوشته، سپس از آن مشتق گرفته شود. به‌منظور انجام این کار ابتدا به ساکن تابع لگاریتمی به ترتیب زیر نوشته شده، سپس به لگاریتم در مبنای e تبدیل می‌شود.

$${\log _ a} x = \frac{ { \ln x } } { { \ln a} }$$

حال با استفاده از قانون مشتق‌گیری کسری، از طرفین رابطه فوق مشتق می‌گیریم. با انجام این کار داریم:

$$\begin {align*}\frac{ d } { { d x } } \left( {{{\log } _ a} x} \right) & = \frac{d}{{dx}}\left( {\frac{{\ln x}}{{\ln a}}} \right)\\ & = \frac{1} { {\ln a}}\frac{ d } { { d x } } \left( { \ln x} \right )\\ & = \frac { 1 } { { x \ln a } }\end{align*}$$

توجه داشته باشید که در بدست آوردن رابطه بالا از ثابت بودن ln a استفاده شده است. نهایتا مشتق تابع لگاریتمی برابر با رابطه زیر بدست می‌آید.

$$\frac{ d } { { d x } } \left( { { { \log } _ a} x } \right) = \frac { 1 } { { x \ln a } }$$

نهایتا به‌طور خلاصه مشتق توابع نمایی و لگاریتمی را می‌توان با استفاده از روابط زیر بدست آورد.

$$\boxed {\begin{array}{ll}\displaystyle \frac{ d } { { d x } }\left( {{{\bf{e}}^x}} \right) = {{\bf{e}} ^ x} & \hspace{1.0in}\displaystyle \frac{ d }{{ d x }}\left( {{a^x}} \right) = {a ^ x}\ln a\\ \displaystyle \frac{ d } {{ d x }}\left( {\ln x} \right) = \frac{1}{ x } & \hspace{1.0in}\displaystyle \frac{ d }{{ d x }}\left( {{{\log } _ a} x} \right) = \frac{ 1 }{{ x \ln a }}\end{array}}$$

در ادامه مثال‌هایی حل شده که به منظور تسلط به موضوع می‌توانید آن‌ها را مطالعه فرمایید.

مثال ۱

مشتق توابع زیر را بدست آورید.

1. $$R \left( w \right) = { 4 ^ w} - 5{ \log _9} w$$
2. $$f \left ( x \right) = 3 { { \bf { e } } ^ x } + 10 { x ^ 3 } \ln x$$
3. $$\displaystyle y = \frac { { 5 { { \bf { e } } ^ x } } } { { 3 { { \bf{ e }} ^ x } + 1}}$$

حل ۱: بدیهی است که نمی‌توان به صورت عادی از این رابطه مشتق گرفت. در حقیقت بایستی از مشتق تابع ln x و $$e ^ x$$ استفاده کرد. مشتق این تابع برابر است با:

$$R ^{\prime} \left( w \right) = { 4 ^ w } \ln 4 - \frac{ 5 } { { w \ln 9 } }$$

حل ۲: به‌منظور محاسبه مشتق تابع شماره ۲ بایستی از قانونِ مشتق‌گیری توابعِ ضرب شده در یکدیگر به صورت زیر استفاده کرد.

$$\begin{align*}f ^{\prime} \left( x \right) & = 3 { { \bf{ e } } ^ x } + 3 0 { x ^ 2 } \ln x + 1 0 { x ^ 3}\left( {\frac{1}{x}} \right)\\ & = 3 { {\bf { e } } ^ x } + 30 { x ^ 2 } \ln x + 10 { x ^ 2 }\end{align*}$$

حل ۳: به‌منظور محاسبه این مشتق، تنها کافی است از قانون مشتق‌گیری زنجیره‌ای به‌صورت زیر استفاده کرد.

$$\begin{align*} y ^{\prime} & = \frac{ { 5 {{\bf{e}}^x}\left( {3 { {\bf{ e }} ^ x} + 1} \right) - \left( { 5 { { \bf{ e }} ^ x}} \right)\left( {3{{\bf{e}}^x}} \right)}}{{{{\left( {3{{\bf{e}}^x} + 1} \right)}^2}}}\\ & = \frac{{15{{\bf{ e } } ^ { 2 x }} + 5 {{\bf{e}} ^ x} - 15{{\bf{e}}^{ 2 x } }}}{{{{\left( {3{{\bf{ e } } ^ x} + 1} \right)}^2}}}\\ & = \frac{{5{{\bf { e } } ^ x }}}{{{{\left( {3{{\bf{e}}^x} + 1} \right)}^2}}}\end{align*}$$

مثال ۲

فرض کنید موقعیت یک جسم مطابق با رابطه زیر توصیف شود.

$$s \left ( t \right) = t { { \bf { e } } ^ t }$$

آیا این جسم با گذشت زمان می‌ایستد یا همواره سرعتش غیر صفر است؟

حل: همان‌طور که از قوانین فیزیک کلاسیک می‌دانید، مشتق تابع جابجایی یک جسم نسبت به زمان برابر با سرعت است. بنابراین سرعت جسم در هر لحظه برابر است با:

$$s ^{\prime} \left( t \right ) = { { \bf{ e } } ^ t } + t { { \bf{ e } } ^ t } = \left( {1 + t } \right){ {\bf{ e } } ^ t }$$

رابطه فوق تنها در $$t = - 1$$ صفر می‌شود. با توجه به مثبت بودن زمان می‌توان نتیجه گرفت که سرعت جسم هیچ‌وقت صفر نخواهد شد.

مثال ۳

مشتق تابع زیر را محاسبه کنید.

$$\large y = \frac{{\ln x}}{x}$$

حل: با استفاده از قاعده خارج قسمت از این تابع مشتق می‌گیریم:

$$\large \large \begin {align*} y’ \left ( x \right ) & = { \left ( { \frac { { \ln x } } { x } } \right ) ^ \prime } = { \frac { { { { \left ( { \ln x } \right ) } ^ \prime } \cdot x – \ln x \cdot x’ } } { { { x ^ 2 } } } } \\ & = { \frac { { \frac { 1 } { x } \cdot x – \ln x \cdot 1 } } { { { x ^ 2 } } } } = { \frac { { 1 – \ln x } } { { { x ^ 2 } } } , } \end {align*}$$

که در آن، $$x > 0$$.

مثال ۴

مشتق تابع $$y = x\ln x – x$$ را محاسبه کنید.

حل: با استفاده از قواعد ضرب و تفاضل، داریم:

$$ \large \begin {align*} \require{cancel} y’ \left ( x \right ) & = { \left [ { x \ln x – x } \right ] ^ \prime } = { { \left ( { x \ln x } \right ) ^ \prime } – x’ } = { x’ \ln x + x { \left( {\ln x} \right)^\prime } – x’ } \\ & = {1 \cdot \ln x + x \cdot \frac { 1 } { x } – 1 } = { \ln x + \cancel { 1 } – \cancel { 1 } = \ln x \; \; } \kern-0.3pt { \left ( { x \gt 0 } \right ) . } \end {align*} $$

مثال ۵

مشتق تابع $$y = x\ln {\frac{1}{x}}$$ را به دست آورید.

فیلم آموزش ریاضیات و کاربرد آن در حسابداری، مدیریت و اقتصاد – بخش یکم در فرادرس

کلیک کنید

حل: با استفاده از قاعده ضرب، قاعده زنجیری و مشتق لگاریتم طبیعی، داریم:

$$ \large \begin {align*} \cssId{element14} y ^ \prime & = \left ( { x \ln \frac { 1 } { x } } \right ) ^ \prime = { x ^ \prime \cdot \ln \frac { 1 } { x } + x \cdot \left ( { \ln \frac { 1 } { x } } \right ) ^ \prime } = { 1 \cdot \ln \frac { 1 } { x } + x \cdot \frac { 1 } { { \frac { 1 } { x } } } \cdot \left ( { \frac { 1 } { x } } \right ) ^ \prime } \\ & = { \ln \frac { 1 } { x } + x \cdot x \cdot \left ( { – \frac { 1 } { { { x ^ 2 } } } } \right ) } = { \ln \frac { 1 } { x } – \frac { { \cancel { x ^ 2 } } } { { \cancel { x ^ 2 } } } } = \cssId {element15} { \ln \frac { 1 } { x } – 1 . } \end {align*} $$

مثال ۶

مشتق تابع زیر را به دست آورید:

$$\large y = \ln \left ( { { x ^ 2 } – 2 x } \right )$$

حل: مشتق به سادگی به صورت زیر محاسبه می‌شود:

$$\large { y ^ \prime = \left [ { \ln \left ( { { x ^ 2 } – 2 x } \right ) } \right ] ^ \prime } = { \frac { 1 } { { { x ^ 2 } – 2 x } } \cdot \left ( { { x ^ 2 } – 2 x } \right ) ^ \prime } = { \frac { { 2 x – 2 } } { { { x ^ 2 } – 2 x } } . }$$

مثال ۷

مشتق تابع زیر را محاسبه کنید.

$$\large y = \frac { 1 } { { \ln x } }$$

حل: طبق قاعده توان و قاعده زنجیری، داریم:

$$\large \begin {align*} y ^ \prime & = \left ( { \frac { 1 } { { \ln x } } } \right ) ^ \prime = { \left [ { { { \left ( { \ln x } \right ) } ^ { – 1 } } } \right ] ^ \prime } = { – 1 \cdot { \left ( { \ln x } \right ) ^ { – 2 } } \cdot \left ( { \ln x } \right ) ^ \prime } \\ & = { – \frac { 1 } { { { { \ln } ^ 2 } x } } \cdot \frac { 1 } { x } } = { – \frac { 1 } { { x { { \ln } ^ 2 } x } } . } \end {align*}$$

مثال ۸

مشتق تابع $$y = \ln \left( {\sin x} \right)$$ را محاسبه کنید.

حل: مشتق این تابع، با استفاده از قاعده زنجیره‌ای به شکل زیر محاسبه می‌شود:

$$\large \begin {align*} y ^ \prime & = \left ( { \ln \left ( { \sin x } \right ) } \right ) ^ \prime = { \frac { 1 } { { \sin x } } \cdot \left ( { \sin x } \right ) ^ \prime } \\ & = { \frac { 1 } { { \sin x } } \cdot \cos x } = { \frac { { \cos x } } { { \sin x } } } = { \cot x . } \end {align*}$$

مثال ۹

مشتق تابع $$y = {\log _2}\cos x$$ را محاسبه کنید.

حل: باید مشتق log u را محاسبه کنیم. بدین منظور، می‌نویسیم:

$$\large \begin {align*} y’ \left ( x \right ) & = { \left ( { { { \log } _ 2 } \cos x } \right ) ^ \prime } = { \frac { 1 } { { \cos x \cdot \ln 2 } } \cdot { \left ( { \cos x } \right ) ^ \prime } } \\ & = { \frac { 1 } { { \cos x \cdot \ln 2 } } \cdot \left ( { – \sin x } \right ) } = { – \frac { { \sin x } } { { \cos x \cdot \ln 2 } } } = { – \frac { { \tan x } } { { \ln 2 } } . } \end {align*}$$

این تابع تنها وقتی تعریف شده است که داشته باشیم:

$$\large { \cos x \gt 0, \; \; } \Rightarrow { - \frac { \pi } { 2 } + 2 \pi n \lt x \; } \kern0pt { \lt \frac { \pi } { 2 } + 2 \pi n , \; \; } \kern-0.3pt{ n \in \mathbb { Z } . }$$

مثال ۱۰

مشتق تابع زیر را به دست آورید:

$$\large y = { \log _ 3 } \frac { 3 } { x } + \frac { 3 } { x } .$$

حل: با توجه به خاصیت خطی بودن مشتق و قاعده زنجیره‌ای، خواهیم داشت:‌

$$\large \begin {align*} y’ \left ( x \right ) & = { \left ( { { { \log } _ 3 } \frac { 3 } { x } + \frac { 3 } { x } } \right ) ^ \prime } = { { \left ( { { { \log } _ 3 } \frac { 3 } { x } } \right ) ^ \prime } + { \left ( { \frac { 3 } { x } } \right ) ^ \prime } } \\ & = { \frac { 1 } { { \frac { 3 } { x } \ln 3 } } \cdot { \left ( { \frac { 3 } { x } } \right ) ^ \prime } } + { 3 \cdot { \left ( { \frac { 1 } { x } } \right ) ^ \prime } } = {\frac{x}{{3\ln 3}} \cdot 3 \cdot \left( { – \frac{1}{{{x^2}}}} \right) }+{ 3 \cdot \left( { – \frac { 1 } { { { x ^ 2 } } } } \right ) } \\ & = { – \frac { 3 } { { { x ^ 2 } } } \left ( { \frac { x } { { 3 \ln 3 } } + 1 } \right) } = { – \frac { 3 }{ { { x ^ 2 } } } \cdot \frac { { x + 3 \ln 3 } } { { 3 \ln 3 } } } = { – \frac { { x + 3 \ln 3 } } { { { x ^ 2 } \ln 3 } } . } \end {align*}$$

در این مثال، تابع برای $$x > 0$$ تعریف شده است.

مثال ۱۱

مشتق تابع زیر را به دست آورید.

$$\large y = {\log _3}\left( {4{x^2}} \right)$$

حل: مشتق این تابع برابر است با:

$$\large \begin {align*} y’ \left ( x \right ) & = { \left [ { { { \log } _ 3 } \left ( { 4 { x ^ 2 } } \right ) } \right ] ^ \prime } = { \frac { 1 } { { 4 { x ^ 2 } \ln 3 } } \cdot { \left ( { 4 { x ^ 2 } } \right ) ^ \prime } } \\ & = { \frac { { 8 x } } { { 4 { x ^ 2 } \ln 3 } } } = { \frac { 2 } { { x \ln 3 } } \; \left ( { x \ne 0 } \right ) . } \end {align*}$$

مثال ۱۲

مشتق تابع زیر را به دست آورید:

$$\large y = {x^p}\ln x.$$

حل: با استفاده از قانون ضرب و قانون توان، خواهیم داشت:

$$\large \begin {align*} y ^ \prime & = \left ( { { x ^ p } \ln x } \right ) ^ \prime = { \left ( { { x ^ p } } \right ) ^ \prime \ln x + { x ^ p } \left ( { \ln x } \right ) ^ \prime } \\ & = { p { x ^ { p – 1 } } \cdot \ln x + { x ^ p } \cdot \frac { 1 } { x } } = { p { x ^ { p – 1 } } \ln x + { x ^ { p – 1 } } } \\ & = { { x ^ { p – 1 } } \left ( { p \ln x + 1 } \right ) . } \end {align*}$$

مثال ۱۳

مشتق تابع $$y = \ln \tan \frac{x}{2}$$ را بنویسید.

حل: با استفاده از قاعده زنجیره‌ای، خواهیم داشت:

$$\large { y’ \left ( x \right ) } = { { \left ( { \ln \tan \frac { x }{ 2 } } \right ) ^ \prime } } = { \frac { 1 } { { \tan \frac { x } { 2 } } } \cdot { \left ( { \tan \frac { x } { 2 } } \right ) ^ \prime } . }$$

مشتق داخل پرانتز را اعمال می‌کنیم:

$$\large \begin {align*} y’ \left ( x \right ) & = { \cot \frac { x }{ 2 } \cdot \frac { 1 } { { { { \cos } ^ 2 } \frac { x } { 2 } } } \cdot { \left ( { \frac { x } { 2 } } \right ) ^ \prime } } \\ & = { \frac { { \cos \frac { x } { 2 } } } { { \sin \frac { x } { 2 } } } \cdot \frac { 1 } { { { { \cos } ^ 2 } \frac { x } { 2 } } } \cdot \frac { 1 } { 2 } } = { \frac { 1 } { { 2 \sin \frac { x } { 2 } \cos \frac { x } { 2 } } } . } \end {align*}$$

اکنون از فرمول $$\sin x = 2\sin {\large\frac{x}{2}\normalsize}\cos{\large\frac{x}{2}\normalsize}$$ استفاده کرده و جواب نهایی را به دست می‌آوریم:

$$\large { y’ \left ( x \right ) = \frac { 1 } { { \sin x } } } = { \csc x . }$$