اعداد گویا — به زبان ساده

در وبلاگ فرادرس، مفهوم اعداد حقیقی به صورت کامل مورد بررسی قرار گرفت. اعداد حقیقی مجموعه‌ای از تمام اعداد را در بر می‌گیرند. دسته‌ای از این اعداد را می‌توان به صورت یک کسر و حاصل تقسیم دو عدد صحیح (اعداد صحیح دسته‌ای از اعداد حقیقی مانند عدد 43 را شامل می‌شوند که قسمت اعشاری ندارد) بر یکدیگر بیان کرد. به این دسته از اعداد حقیقی، اعداد گویا گفته می‌شود.

اعداد گویا در زبان انگلیسی با نام Rational Numbers معرفی می‌شوند و این نام از ریشه Ratio به معنای نسبت، گرفته شده است.

مثال‌ها

در ادامه چندین نمونه از اعداد گویا و در قالب چند مثال آورده شده است.

فیلم آموزش ریاضی – پایه هشتم

اینجا کلیک کنید

این مثال‌ها کمک بسیار زیادی به درک اعداد گویا و بررسی انواع مختلف آن می‌کند.

مثال 1

عدد $$1 \over 2 $$ را در نظر بگیرید. این عدد یک عدد گویا است؛ زیرا به صورت حاصل تقسیم عدد یک بر عدد دو نوشته شده است.

مثال 2

عدد 0.75 نیز یکی از اعداد گویا در نظر گرفته می‌شود. زیرا می‌توان آن را به صورت یک کسر به شکل $$3 \over 4 $$ بیان کرد.

آموزش هندسه پایه دهم – هندسه ۱

شروع یادگیری

آموزش ریاضی و آمار ۱ – پایه دهم علوم انسانی

شروع یادگیری

آموزش نگارش – پایه هفتم

شروع یادگیری

آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی

شروع یادگیری

آموزش ریاضی پایه هفتم

شروع یادگیری

آموزش محاسبات سریع ریاضی

شروع یادگیری

آموزش ریاضی – پایه هشتم

شروع یادگیری

آموزش عربی – پایه نهم

شروع یادگیری

آموزش ریاضیات گسسته – پایه دوازدهم

شروع یادگیری

آموزش ریاضی – پایه نهم

شروع یادگیری

مثال 3

عدد 1 نیز علاوه بر آن‌که یک عدد صحیح و طبیعی است، یک عدد گویا نیز در نظر گرفته می‌شود. دلیل این موضوع این است که می‌توان این عدد را به صورت یک کسر به شکل $$1 \over 1 $$ بیان کرد.

مثال 4

مشابه مثال بالا، می‌توان نشان داد که عدد ۲ نیز یک عدد گویا است و می‌توان آن را به شکل یک کسر ($$2 \over 1 $$) بیان کرد.

مثال 5

عدد 2.12 را در نظر بگیرید. این عدد را می‌توان به شکل یک کسر برابر با $$212 \over 100 $$ نیز بیان کرد. بنابراین می‌توان 2.12 را یک عدد گویا در نظر گرفت.

مثال 6

اعدادی که مانند مثال قبل، قسمت اعشاری دارند را معمولا می‌توان به صورت یک کسر نشان داد و هر عددی که بتوان آن را به صورت یک کسر نشان داد، یک عدد گویا است. به عنوان مثال دیگر، عدد 6.6- را فرض کنید. این عدد را می‌توان به صورت $$- {66 \over 10} $$ نیز نمایش داد. بنابراین 6.6- یک عدد گویا است.

اعداد گنگ

توجه شود که دسته‌ای دیگر از اعداد حقیقی موجود هستند که نمی‌توان آن‌ها را به صورت یک کسر نمایش داد.

فیلم آموزش ریاضی – پایه نهم

اینجا کلیک کنید

این اعداد را اعداد گنگ می‌نامند. برای مثال عدد π را در نظر بگیرید. قسمت اعشاری این عدد را می‌توان به شکل زیر تا بینهایت نمایش داد.

بنابراین عدد π را نمی‌توان به صورت یک کسر نمایش داد و آن را یک عدد گنگ می‌نامند. به عنوان یک مثال دیگر از اعداد گنگ، می‌توان به جذر‌هایی که مقدار مشخصی ندارند اشاره کرد. برای مثال، حالت زیر را در نظر بگیرید.

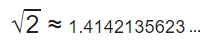
قسمت اعشاری این عدد نیز تا بینهایت ادامه دارد. بنابراین یک عدد گنگ نامیده می‌شود و در دسته‌بندی اعداد گویا قرار نمی‌گیرد.

به صورت کلی می توان دسته‌بندی کلی زیر را برای اعداد حقیقی در نظر گرفت.

R اعداد حقیقی را نشان می‌دهد، Q بخشی از اعداد حقیقی است که نشان دهنده اعداد گویا است. Z و N نیز به ترتیب اعداد صحیح و اعداد طبیعی در نظر گرفته می‌شوند. نکته مهمی که باید به آن توجه کرد این است که بین هر دو عدد گویا یک عدد گویا دیگر نیز وجود دارد. دلیل این موضوع این است که میانگین دو عدد گویا نیز یک عدد گویا است.

توجه شود که اعداد مختلط نیز دسته‌ای از اعداد هستند که از دو بخش تشکیل می‌شوند. قسمت اول شامل یک عدد حقیقی است و بخش حقیقی نامیده می‌شود و قسمت دوم نیز بخش موهومی نام دارد.

در صورتی که به مباحث مرتبط در زمینه ریاضیات پایه علاقه‌مند هستید، آموز‌ش‌های زیر به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• مجموعه آموزش‌های ریاضی و فیزیک
• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش دانشگاهی
• اعداد حقیقی — به زبان ساده
• اعداد مختلط – به زبان ساده
• قدر مطلق (Absolute Value) — به زبان ساده
• گرادیان (Gradient) در ریاضیات — به زبان ساده

^^