توابع نمایی و عدد e – به زبان ساده

برخی افراد همیشه با دیدن e وحشت‌زده می‌شوند؛ البته منظور ما e به عنوان یک مفهوم ریاضیاتی است و نه یک حرف زبان انگلیسی. معنی e در چارچوب ریاضیات دقیقاً چیست؟

کتاب‌های فراوان و حتی ویکی‌پدیا e را چنین تعریف کرده‌اند:

یک ثابت ریاضیاتی که مبنایی برای لگاریتم طبیعی است.

و زمانی که به مدخل لگاریتم طبیعی مراجعه می‌کنیم، تعریف زیر را می‌بینیم:

لگاریتم طبیعی که به طور رسمی لگاریتم هیپربولیک (هذلولوی) نامیده می‌شود، لگاریتمی در مبنای e است که e یک ثابت گنگ تقریباً برابر با 2.718281828459 است.

می‌بینید که این تعریف‌ها به صورت دوری به همدیگر ارجاع می‌دهند. این تعریف گرچه صحیح است؛ اما مفید نیست. بسیاری از توضیح‌های مفاهیم ریاضیاتی خشک و رسمی هستند؛ اما این تعریف برای افراد مبتدی که می‌خواهند با موضوع آشنا شوند، هیچ فایده‌ای ندارد و واقعیت این است که همه ما روزی مبتدی بوده‌ایم.

در این نوشته قصد داریم بینش‌های شهودی و سطح بالای خود را در مورد ماهیت e و طرز کار آن ارائه کنیم. کتاب‌های ریاضیات خود را فعلاً کناری بگذارید چون به آن‌ها نیاز ندارید.

e صرفاً یک عدد نیست

توصیف عدد e به صورت «یک ثابت که تقریباً برابر با ...2.71828» مانند این است که بگوییم عدد پی «یک عدد گنگ تقریباً برابر با ...3.1415» است. بدیهی است که این تعریف صحیح است؛ اما هیچ کمکی به درک ماهیت عدد پی نمی‌کند.

پی نسبت بین محیط و قطر دایره است. این یک نسبت بنیادی است و در همه دایره‌ها وجود دارد، لذا در مورد محاسبه محیط، مساحت، حجم و محیط سطحی همه دایره‌ها، کره‌ها، استوانه‌ها و موارد مشابه کاربرد دارد. پی مهم است و نشان می‌دهد که همه دایره‌ها شبیه هم هستند و لازم به یادآوری نیست که توابع مثلثاتی (سینوس، کسینوس، تانژانت و ...) نیز از دایره‌ها مشتق می‌شوند.

e مبنای نسبت رشد است که در همه فرایندهای رشد پیوسته مشترک است. e به ما امکان می‌دهد که یک نرخ رشد ساده (مثلاً مواردی که همه تغییرات در انتهای یک سال رخ می‌دهند) را انتخاب کنیم و تأثیر ترکیبی آن بر رشد مداوم را که در آن فرایند هر نانوثانیه یا سریع‌تر از آن، اندکی رشد می‌کند را محاسبه کنیم.

e هر جا که سیستم‌هایی به صورت مداوم و نمایی رشد می‌کنند، مشاهده می‌شود. این سیستم‌ها شامل جمعیت، واپاشی رادیواکتیو، محاسبه سود و موارد دیگر است. حتی سیستم‌های ناهموار که رشد همواری ندارند را نیز می‌توان به وسیله e تخمین زد.

همان طور که هر عددی را می‌توان نسخه مقیاس یافته‌ای از 1 (واحد مبنا) دانست، هر دایره را نیز می‌توان نسخه مقیاس یافته‌ای از دایره واحد (با شعاع 1) دانست و هر نرخ رشدی را می‌توان یک نسخه مقیاس یافته از e (رشد مبنا) در نظر گرفت.

بنابراین e یک عدد غیر شفاف به ظاهر تصادفی نیست. e این ایده را نشان می‌دهد که همه سیستم‌های در حال رشد نسخه مقیاس یافته‌ای از یک رشد مشترک هستند.

درک رشد نمایی

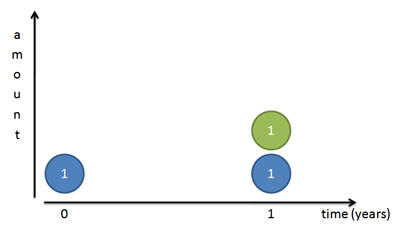
توضیح خود را با یک سیستم مبنا آغاز می‌کنیم که پس از مقدار معینی از زمان دو برابر می‌شود. برای نمونه:

• باکتری‌ها می‌توانند هر 24 ساعت یک بار دو برابر شوند.
• زمانی که رشته‌های نودل را می‌بریم، دو برابر قبل رشته خواهیم داشت.
• اگر نرخ سود سالانه 100% روی سرمایه خود داشته باشید، هر سال سرمایه شما دو برابر خواهد شد.

این وضعیت چیزی شبیه تصویر زیر است:

افراز به دو یا دو برابر کردن، یک فرایند پیشروی متداول است. بدیهی است که می‌توانیم وضعیت‌های سه برابری یا چهار برابری را نیز در نظر بگیریم؛ اما وضعیت دو برابری راحت‌تر است و از این رو در ادامه از آن برای توضیح e استفاده می‌کنیم.

از نظر ریاضیاتی اگر ما x افراز داشته باشیم، در این صورت 2^x آیتم خواهیم داشت. با 1 افراز ما 2¹ یا 2 آیتم داریم. با 4 افراز ما 2⁴ یعنی 16 آیتم خواهیم داشت. به طور کلی به عنوان یک فرمول عمومی:

رشد = 2^x

به بیان دیگر دو برابر کردن، همان رشد 100% است. بنابراین می‌توانیم فرمول فوق را به صورت زیر بازنویسی کنیم:

این همان معادله است؛ فقط 2 را به آن چیزی که واقعاً هست تغییر داده‌ایم، یعنی مقدار 1 اولیه به علاوه 100%.

البته می‌توانیم هر عددی را به جای 100% جایگزین کنیم، مثلاً 50%، 25% یا 200% و فرمول رشد را برای آن نرخ رشد به دست آوریم. بنابراین فرمول عمومی برای x دوره از بازدهی به صورت زیر است:

این به آن معنی است که رشد بازدهی ما (1 + بازدهی)، x بار تکرار شده است.

نگاهی نزدیک‌تر

ما در فرمول خود فرض می‌کنیم که رشد در گام‌های گسسته‌ای صوت می‌پذیرد. باکتری‌ها صبر می‌کنند، صبر می‌کنند و بعد ناگهان دو برابر می‌شوند. یا دریافت سود به طور ناگهانی در پایان سال به طور یکباره انجام می‌یابد. بر اساس فرمول فوق رشد تعویق می‌شود و بعد آنی صورت می‌گیرد. نقطه‌های سبز رنگ در نمودار فوق ناگهان ظاهر می‌شوند.

فیلم آموزش مت کد Mathcad برای استانداردسازی محاسبات و طراحی مهندسی در فرادرس

کلیک کنید

البته این وضعیت همیشه برقرار نیست. اگر نمودار را بزرگنمایی کنیم می‌بینیم که کلونی باکتری در طی زمان دو برابر شده است:

نقطه‌های سبز ناگاهان نمایان نمی‌شوند؛ بلکه به تدریج از نقطه‌های آبی رنگ رشد می‌یابند و پس از یک دوره که در این مورد 24 ساعت است، به اندازه نقطه‌ آبی می‌رسند. سپس به یک نقطه کامل آبی تبدیل می‌شوند و می‌توانند خود نقاط سبز رنگی تولید کنند. آیا این اطلاعات تغییری در معادله ما ایجاد می‌کند؟

پاسخ منفی است. در مورد مثال باکتری نقطه‌های نیمه تشکیل یافته‌ی سبز رنگ، همچنان می‌توانند کاری بکنند تا این که کامل رشد یابند و از والدین آبی رنگ خود جدا شوند؛ اما معادله همچنان برقرار است.

پول همه چیز را تغییر می‌دهد

اما پول همه چیز را تغییر می‌دهد. به محض این که یک ریال سود دریافت کنیم، این سودِ ما می‌تواند خود سودهای جدیدی تولید کند. لازم نیست صبر کنیم تا یک مبلغ معینی سود دریافت کنیم، تا بتوانیم سودهای جدیدی از آن کسب کنیم.

بر اساس فرمول قبلی‌مان، رشد سود مانند زیر است:

اما در این مورد نیز این نمودار کاملاً صحیح نیست، چون همه سودها در روز آخر ظاهر شده‌اند. اگر این نمودار را بزرگنمایی کنیم و یک سال را به دو بخش تقسیم کنیم، خواهیم دید که ما 100% سود را هر سال دریافت می‌کنیم و لذا در بازه 6 ماهه 50% سود دریافت می‌کنیم. بنابراین در شش ماه نخست، 50 سنت دریافت می‌کنیم و 50 سنت دیگر نیز در نیمه دوم سال می‌گیریم:

اما این فرمول همچنان صادق است. بدیهی است که دلار اولیه ما (نقطه آبی رنگ) در طی یک سال یک دلار سود تولید می‌کند؛ اما پس از 6 ماه یک سود 50 سنتی داریم و نکته‌ای که نادیده گرفته‌ایم، همین جا است. این 50 سنت می‌تواند برای خودش سود داشته باشد:

از آنجا که نرخ رشد ما 50% برای نصف سال است، این 50 سنت در این مدت 25 درصد سود می‌دهد (یعنی 50% 50 سنت) و در پایان سال ما وضعیت زیر را داریم:

• دلار اولیه ما (نقطه آبی)
• دلاری که نقطه آبی به صورت سود تولید کرده است (نقطه سبز)
• 25 سنتی که نقطه سبز رنگ، سود داده است (نقطه قرمز)

در این وضعیت در مجموع 2.25 دلار خواهیم داشت. ما 1.25 دلار را از دلار اولیه به دست آورده‌ایم و این حتی از سود دو برابری نیز بهتر است. اجازه بدهید سود خود را به فرمول تبدیل کنیم. رشد دو نیمه 50% به صورت زیر است:

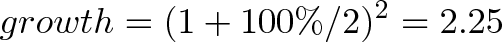
بررسی رشد ترکیبی

اینک زمان آن رسیده است که یک گام فراتر برویم. به جای افراز رشد، به دو نیمه 50 درصدی، این بار آن را به سه بخش 33 درصدی تقسیم می‌کنیم. چه کسی گفته است، ما باید 6 ماه صبر کنیم تا سود خود را به دست آوریم؟ اینک سود خود را بیشتر تقسیم می‌کنیم. نمودار رشد دوره‌های 3 بخشی تصویر جالب زیر را تولید می‌کند:

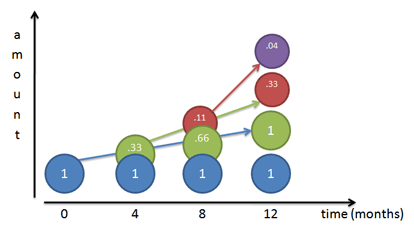
هر رنگ را به عنوان پولی تصور کنید که از رنگ‌های قبلی در دوره‌های 33% تولید می‌شود.

• ماه 0: کار خود را با نقطه آبی 1 دلاری آغاز می‌کنیم
• ماه 4: نقطه آبی 3/1 دلار از خود سود تولید کرده و نقطه سبز رنگ به ارزش 33 سنت ایجاد شده است.
• ماه 8: نقطه آبی 33 درصد دیگر دریافت کرده است و آن را به نقطه سبز داده است و حال نقطه سبز 66 سنت دارد. نقطه سبز در واقع 33% سود از مقدار قبلی خود دریافت کرده است که معادل 11 سنت (33 درصد از 33 سنت) است. این 11 سنت به نقطه قرمز تبدیل می‌شود.
• ماه 12: اینک همه چیز عجیب و غریب شده است. نقطه آبی 33 سنت دیگر دریافت کرده است و آن را به نقطه سبز داده است و نقطه سبز اینک یک دلار کامل دارد. نقطه سبز 33% سود در بازه 8 ماهه دریافت کرده است (معادل 66 سنت) که 22 سنت آن را به نقطه قرمز می‌دهد که در مجموع 33 سنت دارد. همچنین نقطه قرمز که کار خود را با 11 سنت آغاز کرده است، 4 سنت از خود سود کرده است که آن را به نقطه بنفش می‌دهد.

می‌بینید که در انتهای 12 ماه، ما 1 + 1 + 0.33 + 0.04 یعنی در حدود 2.37 دلار پول داریم.

در ادامه مراحل چنین رشدی را توضیح داده‌ایم:

• هر رنگ از سرمایه خود مستقلاً سود می‌گیرد و آن را به رنگ دیگر می‌دهد. پول جدیداً خلق شده می‌تواند خودش پول تولید کند و این چرخه تداوم می‌یابد.
• بهتر است مقدار اولیه (نقطه آبی) را این صورت تصور کنیم که گویی هرگز تغییر نمی‌یابد. نقطه آبی سود خود را برای ایجاد نقطه سبز می‌دهد که مقدار ثابت 33 سنت در هر 44 ماه است. نقطه آبی تغییر نمی‌یابد. در نمودار فوق نقطه آبی یک فلش آبی دارد که نشان می‌دهد نقطه سبز را تغذیه می‌کند.
• نقطه سبز، خود نقطه قرمز را ایجاد و آن را تغذیه می‌کند؛ اما نقطه آبی از آن آگاه نیست.
• وقتی نقطه سبز در طی زمان جلو می‌رود (به طور مداوم از نقطه آبی تغذیه می‌کند) مشارکت بیشتری در طی ماه‌های 4 تا 8 در نقطه قرمز می‌کند. نقطه سبز 11 سنت در طی ماه‌های 8 تا 12 به نقطه قرمز می‌دهد. نقطه سبز 22 سنت به نقطه سبز می‌دهد چون نقطه سبز در طی 8 ماه 66 سنت سود کرده است. اگر این نمودار را بسط دهیم، می‌بینیم که نقطه سبز 33 سنت به نقطه قرمز داده است و بدین ترتیب نقطه سبز در انتهای ماه 12 به یک دلار کامل دست یافته است.

گرچه مفاهیم فوق، ممکن است در ابتدا کمی دشوار به نظر برسد؛ ولی وقتی به دقت بررسی کنید، کاملاً متوجه می‌شوید. حتی ما نیز وقتی این نمودارها را تهیه می‌کردیم، اندکی دچار سردرگمی شدیم؛ اما تصور ایم که هر دلار مستقلاً سودهایی تولید می‌کند که آن‌ها نیز به نوبه خود سود می‌دهند به درک بهتر آن کمک می‌کند.

با در نظر گرفتن دوره‌های 3 ماهه رشد معادله ما به صورت زیر در می‌آید:

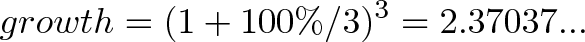
ما در این روش 1.37 دلار سود کرده‌ایم که حتی از 1.25 دلار قبلی نیز بهتر است.

آیا می‌توانیم بی‌نهایت پول در بیاوریم؟

اینک سؤال طبیعی که پیش می‌آید این است که وقتی دوره‌های زمانی را کوچک‌تر می‌کنیم، سود ما افزایش می‌یابد، چرا نباید دوره‌های باز هم کوچک‌تری را انتخاب کنیم؟ مثلاً هر ماه، هر روز، هر ساعت یا حتی هر نانوثانیه؟ آیا در این صورت سود ما رو به آسمان نمی‌گذارد؟

البته در چنین وضعتی سود ما بهبود می‌یابد؛ اما این بهبود سقف معینی دارد. با بررسی اعداد مختلف n در فرمول جادویی‌مان بازده کل را می‌توانیم در ادامه ببینید:

n          (1 + 1/n)^n
-----------------------
1          2
2          2.25
3          2.37
5          2.488
10         2.5937
100        2.7048
1,000      2.7169
10,000     2.71814
100,000    2.718268
1,000,000  2.7182804
...

این عدد رفته رفته افزایش می‌یابد و حول عدد تقریبی 2.718 همگرا می‌شود. می‌بینید که این همان عدد e است.

به بیان فنی ریاضیاتی e طوری تعریف شده است که برابر با نرخ رشد در صورت ترکیب مداوم بازده 100 درصدی در طی بازه‌های زمانی کوچک باشد:

این عدد به نظر می‌رسد که سقف همگرایی باشد و اثبات‌هایی نیز برای آن وجود دارد. اما همان طور که می‌بینید ما هر چه بازه‌های زمانی کوچک‌تر را انتخاب کنیم بازده کل پیرامون عدد 2.718 همگرا می‌شود.

همه این‌ها به چه معنی هستند؟

عدد (...e (2.718 بیشینه نتیجه ممکن هنگام ترکیب نرخ رشد 100 درصدی در طی یک بازه زمانی است. بدیهی است که ما در ابتدا انتظار داشتیم که نرخ بازده 100 درصدی داشته باشیم و 1 دلار خود را 2 دلار بکنیم. اما با گامی کوچک می‌توانیم سود خود را اندکی افزایش دهیم و اجازه بدهیم که از سود خود نیز سود تولید کنیم. اما در نهایت این مقدار 2.718 دلار خواهد بود و این مقدار بیشینه‌ای است که می‌توان از نرخ بهره ترکیبی به دست آورد.

بنابراین اگر با 1 دلار آغاز کنیم و به طور مداوم سود خود را با نرخ بازدهی 100% ترکیب کنیم در نهایت به مقدار 1e می‌رسیم. اگر با 2 دلار آغاز کنیم به مقدار 2e می‌رسیم و اگر با 11.79 دلار آغاز کنیم به مقدار 11.79e می‌رسیم.

e مانند یک محدودیت سرعت است که میزان سرعت رشد شما را در صورتی که به طور مداوم پیشروی کنید نشان می‌دهد. شما ممکن است همیشه به این سقف سرعت نرسید؛ اما e یک نقطه مرجع است و می‌توانید هر نرخ رشدی را بر حسب این ثابت جهانی بنویسد.

نکته: در مورد جدا کردن مقدار افزایش از نتیجه نهایی مراقب باشید. وقتی 1 به (...2.718) e می‌رسد، میران رشد (نرخ رشد) 171.8%e خود نتیجه نهایی است که پس از همه رشد به آن می‌رسیم (مقدار اصلی به علاوه افزایش).

در مورد نرخ‌های رشد دیگر چه می‌توان گفت؟

اگر با نرخ رشد 50% سالانه به جای 100% سرمایه‌گذاری کنیم آیا همچنان می‌توانیم از e استفاده کنیم؟

فیلم آموزش روابط بازگشتی در ریاضیات گسسته (رایگان) در فرادرس

کلیک کنید

در ادامه پاسخ این سؤال را بررسی می‌کنیم. نرخ 50% نرخ رشد ترکیبی است که به صورت زیر محاسبه می‌شود:

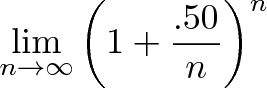
باید دید در این جا چه می‌شود کرد؟ به خاطر دارید که 50% کل بازده است و n تعداد دوره‌های افراز رشد برای محاسبه است. اگر n=50 در نظر بگیریم می‌توانیم نرخ رشد را 50 بخش با بهره 1% تقسیم کنیم:

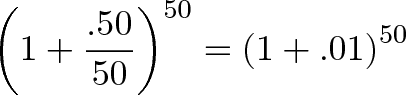
بدیهی است که این مقدار بی‌نهایت کوچک نیست؛ اما در هر صورت آن را کاملاً خرد کرده‌ایم. اینک تصور کنید که نرخ معمول 100% خود را نیز به بخش‌های 1% تقسیم می‌کردیم:

در این جا به نتیجه‌ای می‌رسیم. در حالت معمول ما 100 تغییر تجمعی 1 درصدی داریم. در مورد سناریوی فوق 50 تغییر تجمعی 1% داریم.

تفاوت بین این دو عدد چیست؟ می‌توان گفت که این تنها نصف آن عدد است.

این نتیجه کاملاً جذاب است، چون 0.5=100/50 همان توانی است که e را به آن می‌رسانیم. این واقعیت به طور کلی نیز صحیح است. اگر ما نرخ رشد 300% داشته باشیم، می‌توانیم آن را به 300 بخش 1 درصدی تقسیم کنیم. بدین ترتیب مقدار معمول برای یک نرخ خالص e³ سه برابر می‌شود.

با این که رشد می‌تواند مانند جمع (1+%) به نظر برسد، اما باید به خاطر داشته باشیم که در واقع این ضرب (1.01×) است. به همین دلیل است که ما از توان (یعنی ضرب مکرر) و ریشه‌های مربع (e^1/2 یعنی نصف تعداد تغییرات یا به عبارت دیگر نصف تعداد ضرب‌ها) استفاده می‌کنیم.

با این که ما عدد 1% را انتخاب کرده‌ایم، با این حال می‌توانستیم واحد کوچک‌تری نیز برای رشد انتخاب کنیم، مثلاً 0.1%، 0.0001% و یا حتی مقادیر بسیار کوچک‌تر. نکته کلیدی این است که هر نرخ رشدی انتخاب کنیم، صرفاً یک نمای e است.

رشد = e^نرخ

در مورد دوره‌های زمانی دیگر چه می‌توان گفت؟

فرض کنید نرخ رشد 300% را برای دو سال داشته باشیم. در این صورت ما رشد یک ساله (e³) را در خودش ضرب کرده‌ایم:

و به طور کلی

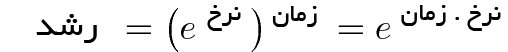
به دلیل همین ویژگی جادویی در توان‌ها، لازم نیست دو توان داشته باشیم و صرفاً نرخ را در زمان ضرب کرده و در یک توان واحد نمایش دهیم.

راز بزرگ: e همزمان نرخ رشد و دوره زمانی را در خود ادغام می‌کند

این واقعیت اندکی عجیب است. e^x همزمان می‌تواند واجد دو معنا باشد:

• X تعداد دفعاتی است که ما نرخ رشد را صرب می‌کنیم، یعنی 100% رشد سالانه برای سه سال برابر با e³ است.
• X نشان‌دهنده خود رشد نیز هست، یعنی 300% رشد برای یک سال برابر با e³ است.

آیا این همپوشانی باعث سردرگمی نمی‌شود؟ آیا در این صورت فرمول‌های ما از کار نمی‌افتند و دنیا به انتها نمی‌رسد؟

هرگز چنین نیست. هر دو این موارد با هم و کنار هم کار می‌کنند. وقتی می‌نویسیم:

e^x

متغیر x ترکیبی از رشد و زمان است.

X = رشد × زمان

در ادامه این مسئله را بیشتر توضیح می‌دهیم. وقتی با نرخ‌های رشد پیوسته سر و کار داریم، 10 سال رشد با نرخ 3% همان تأثیر کلی 1 سال رشد با نرخ 30% را دارد.

10 سال رشد 3% به معنی 30 تغییر 1% است. این تغییرات در طی 10 سال رخ می‌دهند و از این رو رشد پیوسته شما به صورت 3% سالانه است.

1 دوره رشد 30% یک ساله به معنی 30 تغییر 1% است؛ اما در یک سال منفرد رخ می‌دهد. بنابراین رشد به میزان 30% در یک سال اتفاق افتاده و متوقف شده است.

در هر دو حالت 30 تغییر یک درصدی رخ داده است. هر چه نرخ رشد سریع‌تر باشد (30%)، زمان کمتری برای رشد مورد نیاز است (1 سال). هر چه نرخ رشد کندتر باشد (3%)، مدت طولانی‌تری برای رسیدن به نرخ رشد معین مورد نیاز است (10 سال).

اما در هر دو حالت رشد در نهایت برابر با e³⁰ =1.35 است. ما در اغلب موارد صبر کمی داریم و نرخ‌های رشد بزرگ و سریع را ترجیح می‌دهیم؛ اما e نشان می‌دهد که تأثیر خالص آن‌ها در نهایت یکسان است.

بنابراین فرمول ما به صورت زیر در می‌آید:

رشد = e^x = e^rt

اگر ما بازدهی r را برای t دوره زمانی داشته باشیم،؛ در این صورت رشد پیوسته ما برابر با e^rt خواهد بود. این وضعیت حتی در مورد بازدهی‌های منفی و کسری نیز به همین ترتیب صحیح است.

مثال

بررسی مثال‌ها باعث می‌شوند که یادگیری همه چیز ساده‌تر شود. ما در این بخش به استفاده از فرمول‌هایی مانند 2^x و بهره‌های منظم ترکیبی عادت کردیم. اما در اکثر موارد این فرمول‌ها باعث سردرگمی می‌شوند.

مثال‌هایی که در ادامه مطرح می‌شوند، روی رشد پیوسته و هموار متمرکز هستند و نه رشد یکباره که در بازه‌های یک ساله رخ می‌دهد. روش‌هایی برای تبدیل بین آن‌ها وجود دارد که شاید در مقاله دیگری آن‌ها را بررسی کردیم.

مثال 1: رشد کریستال‌ها

فرض کنید 300 کیلوگرم از یک کریستال جادویی دارد. این ماده به این جهت جادویی است که در طی شبانه‌روز به طور مداوم رشد می‌کند. اگر یک کریستال منفرد را تماشا کنید، می‌بینید که در طی 24 ساعت کریستال‌هایی به اندازه وزن خودش از آن جدا می‌شوند. کریستال‌های فرزند نیز با همین نرخ رشد می‌کنند. اینک سؤال این است که پس از 10 روز چه مقدار کریستال داریم؟

از آنجا که کریستال‌ها بی‌درنگ در حال رشد هستند؛ ما با رشد پیوسته روبرو هستیم. نرخ رشد ما 100% در طی 24 ساعت است و از این رو پس از 10 روز داریم: 300 × e^{1 × 10}. یعنی 6.6 میلیون کیلوگرم از این الماس جادویی.

ممکن است این پاسخ برایتان عجیب باشد. به اختلاف بین نرخ ورودی و خروجی کل توجه کنید. نرخ ورودی میزان تغییرات یک کریستال منفرد است که 100% در 24 ساعت است. نرخ خروجی خالص (e (2.718 است، زیرا کریستال‌های فرزند نیز رشد می‌کنند و برای خود فرزندانی می‌سازند.

در این مورد ما نرخ ورودی را داریم و می‌خواهیم نتیجه کلی را پس از ترکیب کردن همه کریستال‌ها بیابیم. اگر نرخ رشد کلی را داشته باشیم و بخواهیم نرخ رشد یک کریستال واحد را به دست آوریم، باید رو به عقب کار کنیم و در این حالت از لگاریتم طبیعی استفاده می‌شود.

مثال 2: بیشینه نرخ بهره

فرض کنید 120 دلار در یک حساب بانکی داریم و نرخ بهره نیز 5% است. تصور کنید بانک، سخاوت به خرج داده است و بالاترین حالت ترکیب ممکن را برای ما محاسبه می‌کند. پس از 10 سال ما $120 · e^{.05 · 10} یعنی 197.85 دلار خواهیم داشت. البته اغلب بانک‌ها این قدر مهربان نیستند تا بهترین نرخ بهره ممکن را به شما بدهند. اختلاف بین بازدهی واقعی و نرخ بازدهی پیوسته در واقع میزان عدم علاقه‌مندی آن‌ها به شما را نشان می‌دهد!

مثال 3: واپاشی هسته‌ای

فرض کنید 10 کیلوگرم ماده هسته‌ای داریم که به نظر می‌رسد با نرخ 100% سالانه به طور پیوسته دچار فروپاشی می‌شود. پس از 3 سال چه مقدار از این ماده داریم؟

شاید ابتدا فکر کنید واپاشی مداوم با نرخ 100% سالانه بدین معنی است که انتظار داریم در انتهای سال همه ماده را از دست بدهیم، چون هر سال 10 کیلوگرم از دست می‌دهیم.

اجازه بدهید زمانی که چند ماه گذشته و تنها 5 کیلوگرم از ماده را داریم بررسی کنیم. آیا فکر می‌کنید این زمان نیمه سال اول است؟ نه چنین نیست و ما با نرخ 5 کیلوگرم بر سال ماده از دست می‌دهیم و بنابراین یک سال دیگر هنوز داریم.

اینک تصور کنید چند ماه دیگر صبر کرده‌ایم و ماده به 2 کیلو کاهش یافته است. البته اینک با نرخ 2 کیلوگرم بر سال ماده از دست می‌دهیم و بنابراین همچنان یک سال دیگر از ماده رادیواکتیویته داریم (از این لحظه). زمانی که 1 کیلوگرم داشته باشیم، نیز 1 سال دیگر فرصت داریم. زمانی که نیم کیلوگرم داشته باشیم، هم 1 سال دیگر فرصت داریم. آیا متوجه این الگو می‌شوید؟

با گذر زمان ما ماده از دست می‌دهیم؛ اما نرخ واپاشی کندتر می‌شود. این نرخ رشد که به طور مداوم در حال تغییر است جوهره رشد و زوال پیوسته است.

پس از سه سال ما 10 · e^{-1 · 3} از ماده را داریم. ما از توان منفی برای واپاشی (زوال) استفاده می‌کنیم چون می‌خواهیم یک کسر (1/e^rt) در برابر ضریب رشد (e^rt) داشته باشیم. زوال معمولاً با نیمه‌عمر تعریف می‌شود، یعنی زمانی که برای واپاشی نیمی از ماده لازم است. اینک شما می‌دانید e چیست و آن را با عدد پی یا اعداد دیگر اشتباه نمی‌گیرید. e به توان «r*t» تأثیر رشد بر نرخ رشد r و دوره زمانی t را نشان می‌دهد.

سخن پایانی

حال که با e آشنا شدید باید بگوییم که موارد بیشتری هستند که باید بیاموزید:

• توضیح دهید چرا e مهم است - e یک ثابت بنیادی مانند pi است که در نرخ‌های رشد نمایان می‌شود.
• یک توضیح شهودی ارائه دهید – e امکان دیدن تأثیر هر نرخ رشدی را به ما می‌دهد. هر بخش جدیدی از رشد (نقاط سبز و قرمز) به رشد کلی اضافه می‌شوند.
• e چگونه استفاده می‌شود – e^x امکان پیش‌بینی تأثیر هر گونه نرخ رشد و دوره زمانی را فراهم می‌سازد.

این مقاله با همه تلاشی که برای جامع بودن شده است، به هیچ وجه نوشته کاملی در مورد e محسوب نمی‌شود. چون این حوزه‌ای است که جمع کردن همه مطالب در یک نوشته نه در حوصله شما و نه در توان نگارنده است. بنابراین منتظر نوشته‌های بعدی ما از سری مجموعه‌های ریاضیات به زبان ساده باشید. تا آن هنگام می‌توانید دیدگاه‌ها و پیشنهادهای خود را در بخش نظرات با ما و دیگر خوانندگان فرادرس در میان بگذارید.