رفع ابهام حد — به زبان ساده

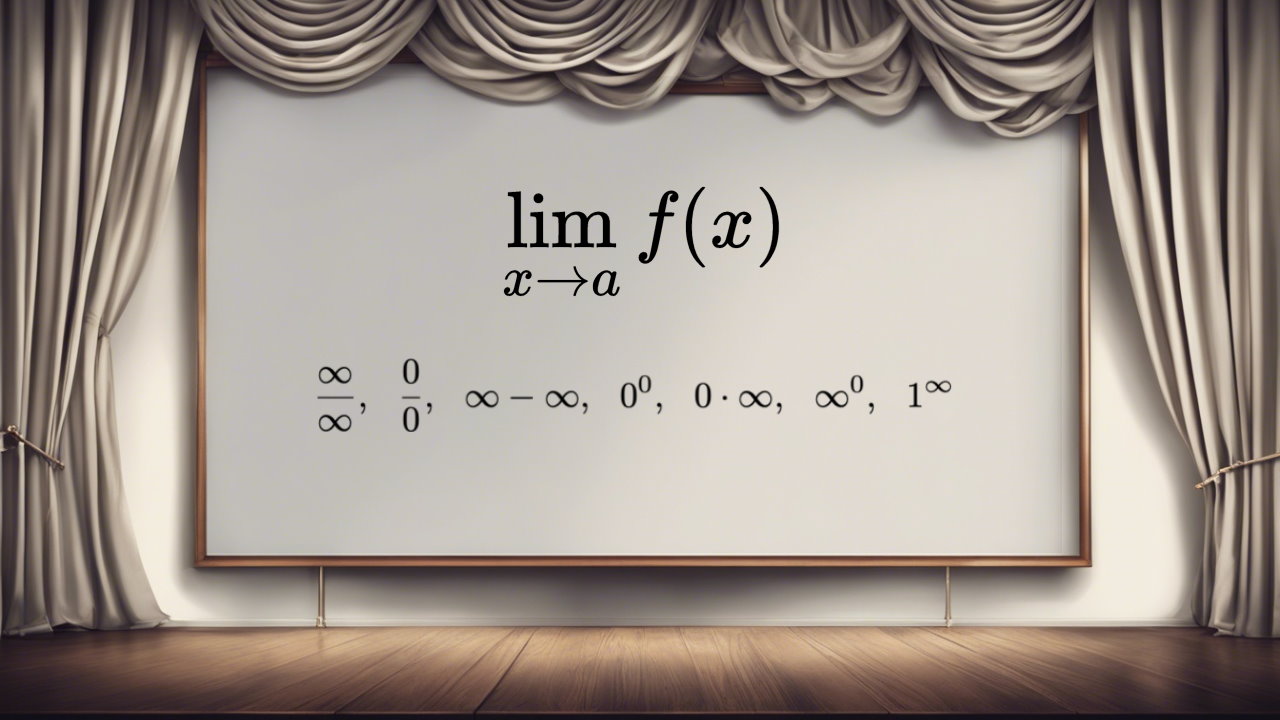
در مطالب پیشین فرادرس مفاهیم حد را توضیح دادیم. از این رو در این مطلب قصد داریم تا روش‌های رفع ابهام حد را توضیح داده و مثال‌هایی از آن ارائه دهیم. البته به منظور درک بهتر پیشنهاد می‌شود مطالب حد، پیوستگی، حد بینهایت و قاعده هوپیتال را مطالعه فرمایید.

رفع ابهام حد $$\large\frac {0}{0}\normalsize$$

فرض کنید توابع f و g در نقطه مشخصی همچون a دارای حد باشند. هم‌چنین اندازه حد در این نقاط را به صورت زیر برابر با صفر در نظر بگیرید.

$$\Large { \lim \limits _ { x \to a } f \left ( x \right ) = 0 \; \; \; } \kern-0.3pt {\text {and} \; \; \lim \limits _ { x \to a } g \left ( x \right ) = 0 }$$

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

با فرض فوق، حاصل حد تابع $$\large \large \frac { { f \left ( x \right ) } } { { g \left ( x \right ) } } \normalsize$$ در نقطه x=a به صورت $$\large \frac { 0 } { 0 }$$ در خواهد آمد. بنابراین این حد در نقطه x=a مبهم بوده و باید آن را رفع ابهام کرد. در چنین مواردی باید عامل صفر شونده را از مخرج و صورت حذف کرد. با استفاده از قواعدی همچون هوپیتال، می‌توان عامل صفر کننده را حذف کرد. البته در این مثال از روش هوپیتال استفاده نکرده و روش‌های جبری را بیان خواهیم کرد.

رفع ابهام حد $$\large\frac{\infty}{\infty}\normalsize$$

در ابتدا فرض کنید حد دو تابع f و g در نقطه x=a به صورت زیر باشند.

$$\large { \lim \limits _ { x \to a} f \left ( x \right) = \pm \infty\;\;\;}\kern-0.3pt {\text{and}\;\;\lim \limits _ { x \to a } g \left ( x \right) = \pm \infty.}$$

در این صورت حد تقسیم این دو تابع در نقطه مذکور برابر است با:

$$\large \lim _ {x \rightarrow a} \frac { f ( x ) } { g ( x ) } = \frac {\infty} {\infty}$$

به منظور یافتن حد چنین توابعی بهتر است تا صورت و مخرج به بزرگ‌ترین توان تقسیم شوند. البته در مثال‌هایی که در ادامه بیان شده، این روش از رفع ابهام را بیشتر توضیح خواهیم داد.

حدود $$\large\infty-\infty,0.\infty,\infty^0 ,1^\infty$$

موارد بیان شده همگی حالت‌های ابهام بوده و باید آن‌ها را رفع ابهام کرد.

فیلم آموزش ریاضی 3 – پایه دوازدهم علوم تجربی در فرادرس

کلیک کنید

این موارد را معمولا می‌توان به حالت $$\large\frac{0}{0}\normalsize$$ یا $$\large \frac{\infty}{\infty}\normalsize$$ تبدیل کرده سپس از روش‌های رفع ابهام مرتبط با آن‌ها استفاده کرد.

مثال‌ها

در ادامه مثال‌هایی مطرح شده که با مطالعه آن‌ها می‌توانید به بسیاری از تکنیک‌های رفع ابهام مسلط شوید.

مثال ۱

حاصل حد زیر را بیابید.

$$\large \lim\limits _ { x \to 1 } { \large \frac { { { x ^ { 20 } } – 1 } } { { { x ^ { 1 0 } } – 1 } } \normalsize}$$

بدیهی است که حاصل صورت و مخرج به ازای x=1 برابر با صفر می‌شود. از این رو این حد مبهم و از نوع $$\large \frac { 0 } { 0 }$$ است. بنابراین می‌توان با حذف کردن عامل صفر در صورت و مخرج پاسخ آن را یافت. در ادامه حاصل این حد محاسبه شده است.

$$\large \require{cancel}<br /> {\lim\limits_{x \to 1} \frac{{{x^{20}} – 1}}{{{x^{10}} – 1}} = \left[ {\frac{0}{0}} \right] }<br /> = {\lim\limits_{x \to 1} \frac { {{{\left( { { x ^ { 10}}} \right)}^2} – 1}}{{{x^{10}} – 1}} }<br /> = {\lim\limits_{x \to 1} \frac{{\cancel{\left( { { x ^ { 10}} – 1} \right)}\left( { { x^ { 1 0} } + 1 } \right)}}{\cancel{{x^{10}} – 1}} }<br /> = {\lim\limits_{x \to 1} \left ( { { x ^ { 10 } } + 1 } \right ) = {1^{10}} + 1 = 2 } $$

مثال ۲

حاصل حد زیر را بیابید.

$$\large \lim \limits _ { y \to – 2 } { \large \frac { { { y ^ 3 } + 3 { y ^ 2 } + 2 y } }{ { {y ^ 2 } – y – 6 } } \normalsize}$$

حاصل این حد در نقطه x=-2 به صورت $$\large \frac { 0 } { 0 }$$ در خواهد آمد. همچون مثال ۱ در این حالت نیز عامل صفر را از صورت و مخرج حذف می‌کنیم. بنابراین خواهیم داشت.

$$\large \begin {align*} { \lim \limits _ { y \to – 2 } \frac{{{y^3} + 3{y^2} + 2y}}{{{y^2} – y – 6}} = \left[ {\frac{0}{0}} \right] } & = { \lim \limits _ { y \to – 2 } \frac { { y \left( {y + 1} \right)\cancel{\left( {y + 2} \right)}}}{{\left( {y – 3} \right)\cancel{\left( {y + 2} \right ) } } } } \\ & = {\lim\limits_{y \to – 2} \frac{{y\left( {y + 1} \right)}}{{y – 3}} = \frac{{\lim\limits_{y \to – 2} y \cdot \lim\limits_{y \to – 2} \left( { y + 1} \right)}} { { \lim\limits_{y \to – 2} \left( {y – 3} \right)}} } \\ & = { \frac { { – 2 \cdot \left ( { – 1} \right ) }} {{ – 5}} = – \frac{2}{5} } \end {align*}$$

مثال ۳

حاصل حد تابع زیر را در بینهایت محاسبه کنید.

$$\large \lim \limits _ { x \to \infty } { \large \frac { { { x ^ 3 } + 3 x + 5}}{ { 2 { x ^3 } – 6 x + 1}}\normalsize}$$

فیلم آموزش ریاضی پایه – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

توجه داشته باشید که همواره به منظور محاسبه حد یک چند جمله‌ای در بینهایت، بزرگ‌ترین توان را نگه داشته و از مابقی صرف نظر کنید. در این حالت نیز می‌بینید که حاصل حد به صورت $$\large \frac { \infty } { \infty }$$ است.

همان‌طور که در بالا نیز بیان شد در چنین مواردی می‌توان با تقسیم کردن صورت و مخرج به بزر‌گ‌ترین جمله، کسر را رفع ابهام کرد. بنابراین حاصل این حد نیز برابر است با:

$$\large \begin{align*} { \lim \limits _ { x \to \infty } \frac { { { x ^ 3} + 3 x + 5 } } { { 2 {x ^ 3 } – 6 x + 1}} = \left[ {\frac { \infty } { \infty } } \right ] } & = { \lim \limits _ { x \to \infty } \frac{{\frac{{{x^3} + 3x + 5}}{{{x^3}}}}}{{\frac{{2{x^3} – 6x + 1}}{{{x^3}}}}} } \\~\\ & = {\lim\limits_{x \to \infty } \frac{{\frac{{{x^3}}}{{{x^3}}} + \frac{{3x}}{{{x^3}}} + \frac{5}{{{x^3}}}}}{{\frac{{2{x^3}}}{{{ x^ 3} } } – \frac { { 6 x} } { { { x ^3 } } } + \frac{ 1 } { {{ x ^ 3 }} }}} } \\~\\ & = {\lim\limits_{x \to \infty } \frac{{1 + \frac{3}{{{x^2}}} + \frac{5}{{{x^3}}}}}{{2 – \frac{6}{{{x^2}}} + \frac{1}{{{x^3}}}}} } \\~\\ & = {\frac{{\lim\limits_{x \to \infty } \left( {1 + \frac{3}{{{x^2}}} + \frac{5}{{{x^3}}}} \right)}}{{\lim\limits_{x \to \infty } \left( {2 – \frac{6}{{{x^2}}} + \frac{1}{{{x^3}}}} \right)}} } \\~\\ & = {\frac{{\lim\limits_{x \to \infty } 1 + \lim\limits_{x \to \infty } \frac{3}{{{x^2}}} + \lim\limits_{x \to \infty } \frac{ 5 }{{{ x ^ 3} }} } } { { \lim\limits_{x \to \infty } 2 – \lim\limits_{x \to \infty } \frac{6}{{{x^2}}} + \lim \limits_{x \to \infty } \frac{1} { { { x ^ 3} }} }} } \\~\\ & = {\frac{{1 + 0 + 0}}{{2 – 0 – 0}} = \frac{1}{2} } \end{align*}$$

در بالا محاسبه این حد طولانی‌ به نظر رسیده است. اما توجه داشته باشید که آن را ذهنی نیز می‌توان محاسبه کرد. بدین منظور کافی است تنها بزرگ‌ترین و کوچک‌ترین جملات در صورت و مخرج را در نظر گرفته و با تقسیم ضرایب آن‌ها به یکدیگر می‌توان به همین پاسخ رسید.

مثال ۴

با استفاده از رفع ابهام حد زیر را محاسبه کنید.

$$\large \lim \limits _ { x \to \infty } \left ( { \sqrt { { x ^ 2 } + 1 } – \sqrt { { x ^ 2 } – 1 } } \right )$$

همان‌‌طور که می‌بینید در هر دو رادیکال حاصل حد برابر با بینهایت است. بنابراین حد فوق مبهم و از نوع $$\large \infty - \infty$$ است. در چنین مواردی معمولا باید تابع را به صورت کسری بیان کرد. به منظور کسری کردن آن، می‌توان عبارت را گویا کرد.

$$\large \begin {align*} { L = \lim \limits _ { x \to \infty } \left ( { \sqrt { { x ^ 2 } + 1 } – \sqrt { { x ^ 2 } – 1 } } \right) } & = { \lim \limits _ { x \to \infty } \frac { { { { \left( { \sqrt { { x ^ 2 } + 1} } \right ) } ^ 2 } – { { \left( { \sqrt { { x ^ 2} – 1} } \right ) } ^ 2 } } } { { \left( {\sqrt { { x ^ 2 } + 1} + \sqrt { { x ^ 2 } – 1} } \right ) } } } \\ & = {\lim \limits _ { x \to \infty } \frac { { { x ^ 2 } + 1 – \left( {{x^2} – 1} \right)}}{{\left( {\sqrt {{x^2} + 1} + \sqrt {{x^2} – 1} } \right)}} } \\ & = {\lim\limits_{x \to \infty } \frac{{\cancel{x^2} + 1 – \cancel{x^2} + 1}}{{\left( {\sqrt {{x^2} + 1} + \sqrt {{ x ^ 2 } – 1} } \right)}} } \\ & = {\lim \limits _ { x \to \infty } \frac{2}{{\left( {\sqrt { { x ^ 2 } + 1} + \sqrt {{x^2} – 1} } \right ) } } } \end {align*}$$

حاصل حد فوق نیز به راحتی و به صورت زیر بدست خواهد آمد.

$$\large {L = \lim \limits _ { x \to \infty } \frac { 2 }{ { \left ( { \sqrt { { x ^ 2 } + 1 } + \sqrt {{ x ^ 2 } – 1 } } \right)}} } = {\frac { { \lim\limits_{x \to \infty } 2}}{{\lim\limits _ {x \to \infty } \sqrt {{x^2} + 1} + \lim\limits_{x \to \infty } \sqrt {{ x ^ 2 } – 1} }} } \sim { \frac { 2 } { { \infty + \infty }} \sim \frac { 2 } { \infty } = 0 }$$

مثال ۵

پاسخ حد زیر را بیابید.

$$\large \lim \limits _ { x \to e} { \large \frac { { \ln x – 1 } } {{ x – e } } \normalsize}$$

فیلم آموزش ریاضی پایه دانشگاهی – جامع و کاربردی در فرادرس

کلیک کنید

این حد را می‌توان با استفاده از تغییر متغیر به $$\large \frac { 0 } { 0 }$$ تبدیل کرد. بدین منظور از تغییر متغیر $$\large x – e = t$$ استفاده می‌کنیم. بنابراین می‌توان گفت:

$$\large x \rightarrow e \ \ \Rightarrow \ \ t \rightarrow 0$$

از این رو حاصل حد را نیز می‌توان به صورت زیر بدست آورد.

$$\large \begin {align*} { \lim \limits _ { x \to e} \frac{{\ln x – 1}}{{x – e}} = \left[ {\frac{0}{0}} \right] } & = {\lim\limits_{t \to 0} \frac{{\ln \left( {t + e} \right) – 1}}{t} } \\ & = {\lim\limits_{t \to 0} \frac{{\ln \left( {t + e} \right) – \ln e}}{t} } \\ & = {\lim\limits_{t \to 0} \left( {\frac{1}{t}\ln \frac{{t + e}}{e}} \right) } \\ & = {\lim\limits_{t \to 0} \ln {\left( {\frac{{t + e}}{e}} \right)^{\large\frac{1}{t}\normalsize}} = \left[ {{1^\infty }} \right] } \\ & = {\lim\limits_{t \to 0} \ln \left[ {{{\left( {1 + \frac{t}{e}} \right)}^{\large\frac{e}{t} \cdot \frac{1}{e}\normalsize}}} \right] } \\ & = {\lim\limits_{t \to 0} \left[ {\frac{1}{e}\ln {{\left( {1 + \frac{t}{e}} \right)}^{\large\frac{e}{t}\normalsize}}} \right] } \\ & = {\frac{1}{e}\ln \left[ {\mathop {\lim }\limits_{\frac{t}{e} \to 0} {{\left( {1 + \frac{t}{e}} \right)}^{\large\frac{e}{t}\normalsize}}} \right] } \\ & = {\frac{1}{e} \cdot \ln e = \frac{1}{e}} \end {align*}$$

در این مطلب مفهوم و روش‌های رفع ابهام حد بیان شدند. البته به منظور رفع ابهام روش‌های بسیاری وجود دارد. در اکثر آن‌ها عبارت باید به صورت $$\large \frac { 0 } { 0 }$$ یا $$\large \frac { \infty } { \infty }$$ در آمده و پس از آن از روش‌های رفع ابهام حد در این دو حالت استفاده شود.