قوانین دمورگان در مجموعه ها — به زبان ساده

قوانین دمورگان بیان میکنند که چگونه میتوان گزارهها و مفاهیم ریاضی را با مکمل یا متضاد آنها مرتبط کرد. در نظریه مجموعهها، قوانین دمورگان، رابطه اجتماع و اشتراک مجموعهها را با مکمل آنها بیان میکنند. این قوانین در منطق گزارهها، عطف و فصل منطقی گزارهها را به نقیض آنها مرتبط میسازند. قوانین دمورگان، در مدارهای منطقی برای سیستمهای کامپیوتری نیز کاربرد دارند. علیرغم گستردگی کاربرد قوانین دمورگان در مجموعهها، گزارهها، مدارهای منطقی و...، ساختار آن ها در هریک از این کاربردها مشابه است.
«قوانین دمورگان» (De Morgan's Laws) رابطه بین مجموعهها و مکملشان را بیان میکنند. این قوانین را میتوان به سادگی در قالب نمودارهای وِن (Venn Diagram) نشان داد. اجتماع مکمل دو مجموعه در شکل زیر نشان داده شده است. طبق قانون دمورگان، مکمل دو مجموعه A و B، برابر با اشتراک مکمل هر یک از آنها، یعنی دو مجموعه و است. علامت c مکمل مجموعه را نشان میدهد.
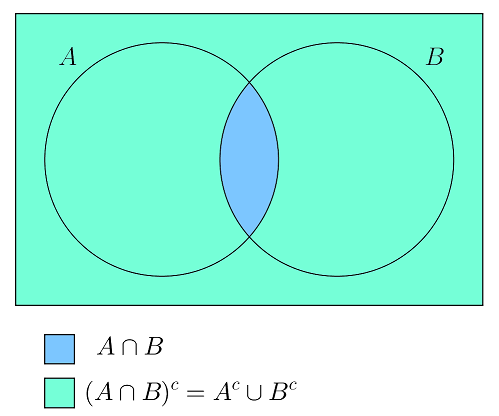
یکی دیگر از قوانین دمورگان بیان میکند مکمل اجتماع دو مجموعه A و B برابر با اشتراک مکمل آن ها، یعنی و است.
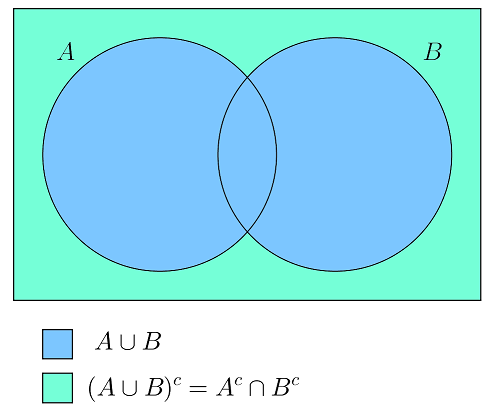
قوانین دمورگان را میتوان به هر تعدادی از مجموعهها تعمیم داد. فرض کنید یکی مجموعه nتایی از مجموعهها باشد. مکمل اشتراک این مجموعهها برابر است با
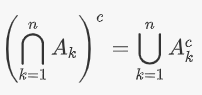
بهطور مشابه میتوان نوشت:
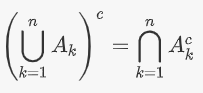
در روابط بالا، نمادهای و ، بهترتیب اشتراک و اجتماع مجموعهها را نشان میدهند.
اگر علاقهمند به موضوعات مشابه و مرتبط به این مطلب هستید، پیشنهاد میکنیم آموزشهای زیر را ببینید:
- مجموعه آموزشهای ریاضیات
- مجموعه آموزشهای ریاضی و فیزیک
- مجموعه آموزشهای دروس رسمی دبیرستان و پیش دانشگاهی
- مجموعه ها در ریاضیات – مفاهیم پایه
- اجتماع، اشتراک و تفاضل مجموعه ها — به زبان ساده
- فهرست مطالب ریاضی وبلاگ فرادرس
^^













لطفا براشون نثال عددی هم بزنید من متوجه نمیشم
داره میگه مثلا اجتماع دو مجموعه مثلا
{2.3.4} و {3.4.5} نسبت به مجموعه مرجع که کلشون میشه یا بیشتر مثلا {2.3.4.5.6}مرجع باشه اگر اجتماع دو مجموعه بخواد میشه {2.3.4.5}
اگر نسبت به مجموعه مرجع بخواد میشه متمم دو مجموعه مثلا یکیشون {3.4.5}بود متمم میشه {2.6} یکی دیگم همینطوری میشه متممش اجتماعشون نسبت به مجموعه مرجع میشه جمع میشه مجموعه مرجع که با U نشون میده منهای متمم جفتشون اگه اشتراک هم داشته باشن باید یک بار منهای اشتراکشون کنی چون دوباره حساب میشه
مثلا این میشه جوابش
َممتم(AUB)-U میشه اجتماع دو مجموعه
یا
(U-A)+(U-B) اینجا همون حالتیه که اگه اشتراک داشته باشن دوبار کم میشه از مجموعه مرجع
که
در مورد تامیم به n مجموعه و شکل ریاضی ای که نوشته بودید مشکل داشتم که این چطوری خونده میشه
چون توی مسائل پایه ای تر به این شکل گزاره ای توضیح داده نشده بود و اشنا نبودم
اگه میشه طرز خوندنش رو هم اشاره کنید تا شاید موضوع شفاف تر و راحت فهم تر بشه
البته فقط این قسمت و بقیه قسمت ها مفید بود
متشکر
با دوستان موافقم یکم نحوه تکلم اذیت میکرد.ولی درکل خیلی ممنون.
خیلی ساده وروان گفته شده
واقعا انتقاد مفیدی بود ?
صداتونو در آخر هر کلمه کش ندین. فقط کلماتو کوتاه بگین.
واقعا انتقاد مفيدي بود ?