جبر خطی مقدماتی — به زبان ساده

در این نوشته قصد داریم به معرفی اجمالی یکی از مهم‌ترین شاخه‌های ریاضی یعنی «جبر خطی» بپردازیم و این کار را از طریق معرفی ماتریس‌ها، دترمینان‌ها، ویژه‌بردارها و ویژه‌مقدارها انجام خواهیم داد. قبل از مطالعه این آموزش، نکات زیر را در نظر داشته باشید:

• تمرکز این آموزش بر مباحثی مانند ماتریس و بردار است.
• مفاهیمی مانند سطر/ستون بر مبنای حافظه به جای توضیح روش استدلالی بررسی می‌شوند.
• از مثال‌های تجریدی (بردارهای 2 بُعدی، 3 بُعدی) و همچنین مثال‌هایی از موضوعات زندگی روزمره استفاده می‌کنیم.

بدین ترتیب، دیگر تنها علاقه‌مندانِ جبر خطی، فیزیکدان‌ها، برنامه‌نویسان گرافیکی و یا سایر مازوخیست‌ها نخواهند بود! زیرا یک اصل مهم این است که:

جبر خطی همان صفحه گسترده‌های کوچکی را که دوست دارید، برای معادلات ریاضی در اختیار شما قرار می‌دهد.

ما می‌توانیم از یک جدول داده‌ها (ماتریس) استفاده کرده و جداول به‌روزرسانی شده‌ای را از جدول اولیه ایجاد کنیم. این قدرت صفحه گسترده (Spreadsheet) است که به صورت یک معادله نوشته می‌شود. در این نوشته مقدمه‌ای بر جبر خطی ارائه می‌کنیم که بر اساس رویه‌های فوق بر مبنای مثال‌هایی از بازار سهام در دنیای واقعی است.

معنی جبر خطی چیست؟

جبر به معنی روابط است. ما در جبر دبیرستانی به بررسی روابط بین اعداد مجهول می‌پرداختیم. با اینکه مقادیر X و Y را نمی‌دانستیم، ولی همچنان می‌توانستیم رابطه زیر را درک کنیم:

(x + y)² = x² + 2xy + y²

جبر خطی به معنی «روابط شبیه خط» است. این مسئله را در ادامه بیشتر توضیح می‌دهیم.

فیلم آموزش جبر خطی در فرادرس

کلیک کنید

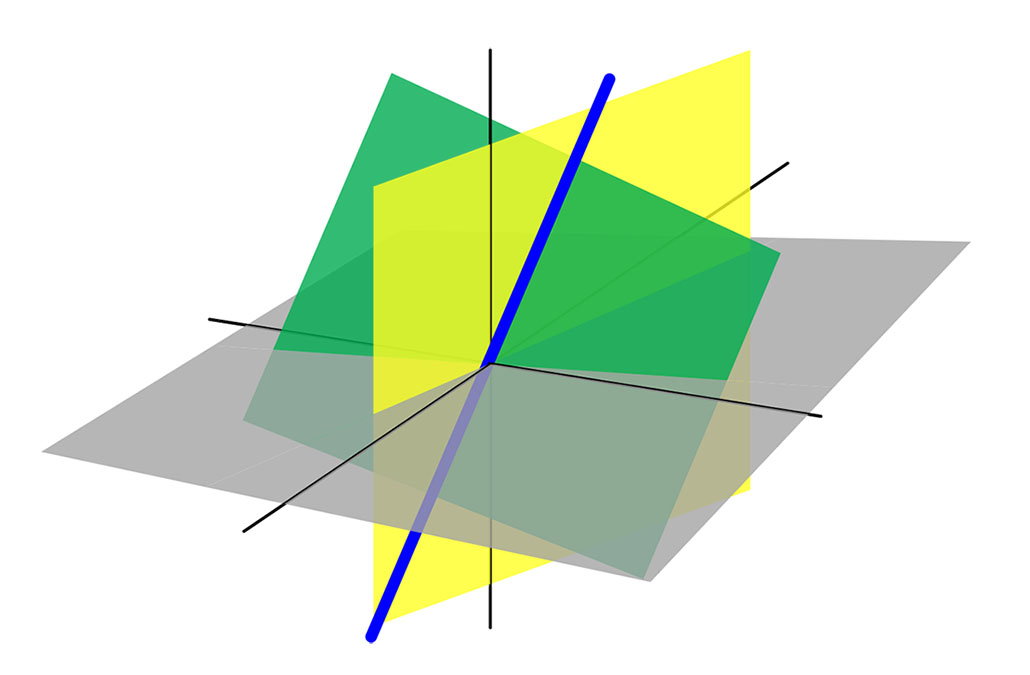
خطوط مستقیم قابل پیش‌بینی هستند. برای مثال یک سقف شیروانی را تصور کنید. اگر سه قدم روی زمین زیر این سقف گام بردارید، این سقف به اندازه یک قدم از زمین فاصله می‌گیرد (شیب سقف 1/3 است) اگر 6 قدم روی زمین به جلو حرکت کنید، انتظار دارید که سقف 2 قدم از زمین فاصله بگیرد. حال یک سقف گنبدی را تصور کنید، هر قدم که روی سطح زمین برمی‌دارید، ارتفاع سقف از زمین به مقدار متفاوتی تغییر پیدا می‌کند. به همین جهت، خطوط، زیبا و قابل پیش‌بینی هستند:

• اگر با حرکت به اندازه 3 قدم، ارتفاع سقف 1 قدم افزایش یابد، اگر 10 برابر فاصله بگیرید، ارتفاع نیز 10 برابر افزایش می‌یابد (یعنی با طی مسافت 30 قدم، ارتفاع سقف 10 قدم افزایش می‌یابد).
• اگر مسافت 3 قدم با افزایش ارتفاع 1 قدم و مسافت 6 قدم با افزایش ارتفاع 2 قدم همراه باشند، در این صورت طی مسافت (3+6) قدم، باعث افزایش (1+2) قدم در ارتفاع سقف می‌شود.

به زبان ریاضی عملیات F را خطی می‌دانیم، در صورتی که مقیاس ورودی با مقیاس خروجی یکسان باشد و افزودن به مقادیر ورودی باعث همان افزایش در خروجی شود:

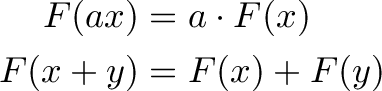
در این مثال تصور کنید تابع (F(x زمانی که x قدم به جلو حرکت می‌کنیم، ارتفاع سقف از زمین را نشان می‌دهد و مشخصات آن به صورت زیر است:

عملیات‌های خطی

منظور از عملیات، محاسبه‌ای مبتنی بر برخی ورودی‌ها است. کدام عملیات‌ها خطی و قابل پیش‌بینی هستند؟ به نظر می‌رسد که ضرب چنین خصوصیتی دارد.

فیلم آموزش جبر خطی – مرور و حل مساله در فرادرس

کلیک کنید

عملیات‌های توان F(x) = x² قابل پیش‌بینی نیستند، چون 10² برابر با 100 است؛ اما 20² نتیجه‌ای برابر با 400 دارد. می‌بینیم که با دو برابر کردن ورودی، مقدار خروجی چهار برابر شده است. نکته شگفت‌انگیز این است که جمع معمولی نیز یک رابطه خطی نیست. برای مثال، تابع «افزایش به اندازه 3» را در نظر بگیرید:

بدین ترتیب ورودی را دو برابر می‌کنیم و می‌بینیم که خروجی دو برابر نشده است. گرچه تابع F(x) = x + 3 تابع یک خطِ دارای عرض از مبداء است، اما همچنان خطی محسوب نمی‌شود؛ زیرا F(10) برابر با 10× F(1) نیست.

تنها امید ما ضرب با یک ثابت است: F(x) = ax. در مثال سقف دیدیم که a=1/3 بود. با این حال می‌دانیم که با ترکیب عملیات‌های خطی می‌توانیم عملیات‌های خطی جدیدی به دست آوریم:

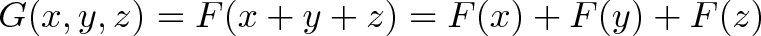
در رابطه بالا، G از سه جمله خطی تشکیل شده است و اگر ورودی را دو برابر کنیم، خروجی نیز دو برابر خواهد شد.

در اینجا کمی باید به محاسبه بپردازیم: ورودی‌ها در یک عدد ثابت ضرب و به نتایج اضافه می‌شوند. در واقع، این کار مفید است، زیرا می‌توانیم ورودی‌ها را از هم جدا کرده، آن‌ها را به صوت منفرد تحلیل کنیم و به ترکیب نتایج با هم بپردازیم:

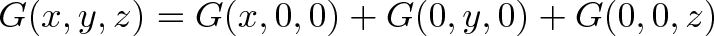
اگر با ورودی‌ها به طور متفاوت (مثلاً بر حسب توان) تعامل داشته باشیم، نمی‌توانیم آن‌ها را از هم جدا کنیم و باید همه چیز را به یک‌باره مورد تحلیل قرار دهیم.

سازمان‌دهی ورودی‌ها و عملیات‌ها

در اغلب مطالب آموزشی، همان ابتدا به جزییات ماتریس پرداخته می‌شود. «خب بچه‌ها امروز قصد داریم صحبت کردن را یاد بگیریم. یک فاعل، یک فعل و یک مفعول انتخاب می‌کنیم. سپس فعل را صرف می‌کنیم و حروف ربط را به جمله اضافه می‌کنیم...». البته که این روش جواب‌گو نیست، چون ایده اصلی جای دیگری است:

• دسته‌ای از ورودی‌ها داریم که می‌خواهیم آن‌ها را ردگیری کنیم.
• عملیات‌های خطی قابل پیش‌بینی برای اجرا داریم.
• سپس نتیجه‌ای به دست می‌آوریم و احتمالاً مجدداً آن را تبدیل می‌کنیم.

فیلم آموزش جبر خطی با متلب در فرادرس

کلیک کنید

اکنون سؤال این است که در گام ابتدایی چگونه می‌توانیم ورودی‌ها را درگیری کنیم. پاسخ در قالب فهرستی است:

X

Y

Z

البته می‌توانیم این فهرست را به صورت (x, y, z) نیز بنویسیم. سؤال بعدی این است که چگونه می‌توانیم عملیات‌های خود را پیگیری کنیم؟ اگر به خاطر داشته باشید صرفاً با برخی محاسبات ساده به صورت ضرب کردن و در نهایت یک عملیات جمع، می‌توانیم عملیات‌ها را انجام دهیم. اگر عملیات F رفتاری مانند زیر داشته باشد:

می‌توانیم کل تابع را به صورت (3, 4, 5) به حالت اختصاری بنویسیم. می‌دانیم که باید ورودی اول را در مقدار نخست، ورودی دوم را در مقدار دوم و همین طور تا آخر ضرب کنیم و در نهایت همه این مقادیر با هم جمع می‌شوند. اگر تنها ورودی اول را نیاز داشته باشیم:

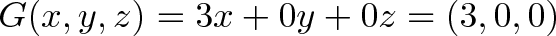
به عبارت دیگر سؤال این است که چگونه می‌توانیم چند مجموعه از ورودی‌ها را مدیریت کنیم؟ برای مثال فرض کنید می‌خواهید عملیات F را روی هر دو مجموعه مقادیر (a, b, c) و (x, y, z) اجرا کنید. بدین منظور آیا می‌توان به صورت زیر عمل کرد؟

می‌دانیم که چنین عملیاتی ناممکن است، چون F به سه ورودی نیاز دارد و نه 6 تا. می‌توانیم این ورودی‌ها را به دو گروه تقسیم کنیم:

1st Input 2nd Input

--------------------

a       x

b       y

c       z

اینک همه چیز واضح‌تر شده است. سؤال بعدی این است که چگونه می‌توانیم ورودی یکسانی را وارد چند عملیات مختلف کنیم؟ بدین منظور می‌توانیم هر دسته از ورودی‌ها را در یک سطر مجزا قرار دهیم:

F: 3 4 5

G: 3 0 0

می‌بینیم که همه چیز سرراست‌تر و سازمان‌یافته‌تر شده است. ورودی‌ها در ستون‌های عمودی قرار گرفته‌اند و عملیات‌ها در سطرهای افقی هستند.

بصری‌سازی ماتریس

شاید کلمات به قدر کافی گویا نباشند و لذا در ادامه، ورودی‌ها، عملیات‌ها و خروجی‌ها را به صورت بصری ارائه کرده‌ایم:

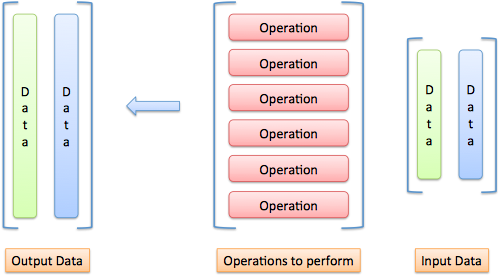
تصور کنید که ورودی‌ها مانند بسته‌هایی هستند که داخل هر عملیات می‌ریزیم:

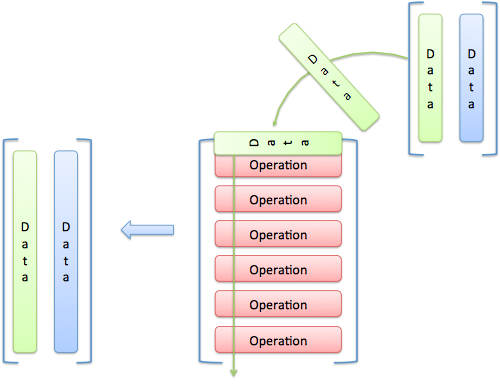
زمانی که یک ورودی از یک عملیات عبور می‌کند، یک آیتم خروجی ایجاد خواهد کرد. در این مثال، ورودی (a, b, c) وارد عملیات F می‌شود و خروجی 3a + 4b + 5c را تولید می‌کند. اگر وارد عملیات G شود، خروجی 3a + 0 + 0 را ارائه می‌دهد.

فیلم آموزش ماتریس ها و جبر خطی – حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

می‌بینیم که یک ماتریس می‌تواند نمودار فوق را به صورت خلاصه نشان دهد:

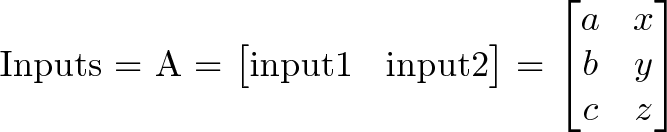
یک ماتریس خود متغیری منفرد است که صفحه گسترده‌ای برای ورودی‌ها و عملیات‌ها ارائه می‌دهد.

ترتیب خوانش ماتریس

در ماتریس‌ها به جای گردش فرایندی مانند (ورودی => ماتریس => خروجی) از نمادگذاری تابعی استفاده می‌کنیم، مثلاً (y = f(x یا f(x) = y. ماتریس معمولاً با یک حرف بزرگ نشان داده می‌شود و ستون‌های منفرد ورودی با حروف کوچک مانند x مشخص می‌شوند. از آنجا که چندین ورودی (A) و چندین خروجی (B) داریم، ماتریس‌ها به صورت زیر هستند:

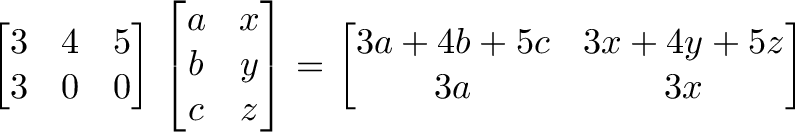
شماره‌گذاری ماتریس‌ها

اندازه ماتریس به صورت RxC محاسبه می‌شود که حرف اول R نشان دهنده تعداد ردیف‌ها و حرف دوم C نماینده تعداد ستون‌ها است و به صورت «m x n» نمایش داده می‌شود. عناصر ماتریس نیز به همین ترتیب مورد ارجاع قرار می‌گیرند: a_ij یعنی عنصر موجود در سطر i و ستون j.

فرض کنید که ماتریس عملیات‌های ما دارای ابعاد 3×2 و ماتریس ورودی‌ها ابعادی برابر با 2×3 داشته باشد. وقتی آن‌ها را با هم بنویسیم، به صورت زیر در می‌آیند:

[Operation Matrix] [Input Matrix]

[operation count x operation size] [input size x input count]

[m x n] [p x q] = [m x q]

[2 x 3] [3 x 2] = [2 x 2]

توجه کنید که نقطه تماس این دو ماتریس «اندازه عملیات» و «اندازه ورودی» یعنی (n=p) است. این دو مقدار باید با هم برابر باشند. اگر ورودی‌های ما 3 مؤلفه داشته باشند، عملیات‌های ما نیز باید سه عنصر داشته باشند. در واقع، ما تنها زمانی دو ماتریس را در هم ضرب کنیم که n=p باشد. ماتریس خروجی، m سطر عملیات برای هر ورودی دارد و با وجود q، ورودی ماتریسی در ابعاد «q x m» خواهیم داشت.

عملیات‌های جالب‌تر

در این بخش اندکی بیشتر با عملیات‌ها روی ماتریس‌ها آشنا می‌شویم. فرض کنید 3 ورودی داشته باشیم، می‌توانیم از یک ماتریس 1-عملیاتی استفاده کنیم:

1. ماتریس جمعی: [1 1 1]
2. ماتریس میانگینی: [1/3 1/3 1/3]

ماتریس جمعی در واقع همان عملیات a + b + c است. ماتریس میانگین‌گیری نیز مشابه آن است: a + b + c)/3 = a/3 + b/3 + c/3).

این عملیات‌های 1 خطی به صورت زیر هستند:

• تنها ورودی اول: [0 0 1]
• تنها ورودی دوم [0 1 0]
• تنها ورودی سوم: [1 0 0]

اگر آن‌ها را به صورت یک ماتریس واحد در هم ادغام کنیم:

[1 0 0]

[0 1 0]

[0 0 1]

این یک ماتریس خاص است که به نام ماتریس همانی نامیده می‌شود. در این ماتریس سه مقدار ورودی بدون هیچ تغییری به یک ماتریس خروجی نگاشت می‌شوند. نظرتان در مورد ماتریس زیر چیست؟

[1 0 0]

[0 0 1]

[0 1 0]

با ارائه ورودی (x, y, z) به این ماتریس، در خروجی ماتریس (x, z, y) را خواهیم داشت. به نظر شما ماتریس زیر چه عملکردی دارد؟

[2 0 0]

[0 2 0]

[0 0 2]

این ماتریس دو برابری است. آن را می‌توانیم به صورت ماتریس 2*I بازنویسی کنیم که در آن I ماتریس همانی است.

زمانی که بخواهیم با ورودی‌ها به صورت مختصات برداری رفتار کنیم، وظیفه ماتریس عملیات، تبدیل ورودی‌های ما خواهد بود. در ادامه، چند مثال از ماتریس‌های تبدیل ارائه کرده‌ایم:

• مقیاس: همه ورودی‌ها را بزرگ/کوچک می‌کند.
• انحراف: برخی ورودی‌ها بزرگ‌تر/کوچک‌تر می‌شوند.
• معکوس: ورودی‌ها را منفی می‌کند.
• چرخش: بر اساس مختصات قبلی، مختصات جدید ایجاد می‌کند؛ یعنی جهت شرق به شمال تبدیل می‌شود، شمال به غرب تبدیل می‌شود و همین طور تا آخر.

موارد فوق تفسیرهای هندسی از عملیات ضرب هستند و روش تبدیل در فضای برداری را نمایش می‌دهند. صرفاً به خاطر بسپارید که بردارها نمونه‌هایی از داده‌هایی هستند که می‌توانیم تغییر دهیم.

مثال غیر برداری: سبد بازار سهام

• داده‌های ورودی: سبد سهام به صورت دلاری از سهام شرکت‌های اپل، گوگل و مایکروسافت
• عملیات‌ها: تغییرات در مقادیر سهام شرکت‌ها پس از یک رویداد خبری
• خروجی: سبد به‌روزرسانی شده

فیلم آموزش روش های عددی در جبر خطی در فرادرس

کلیک کنید

همچنین یک خروجی دیگر هم داریم که به صورت ایجاد یک فهرست از سبد جدید است که در آن سود/زیان خالص ناشی از رویداد مربوطه محاسبه می‌شود.

به طور معمول، ما این وضعیت را در یک صفحه گسترده پیگیری می‌کنیم. اما اکنون این مسئله را در چارچوب جبر خطی بررسی می‌کنیم:

• بردار ورودی می‌تواند به صورت (Apple, Google, Microsoft) باشد که مقدار سرمایه‌گذاری دلاری در سهام هر یک از شرکت‌ها را نشان می‌دهد. توجه داشته باشید که این مقادیر دلاری خود می‌توانند از یک ماتریس دیگر به دست آیند که در آن تعداد سهام‌ها در مبلغشان ضرب می‌شود.
• عملیات‌های خروجی چهارگانه به این صورت هستند: به‌روزرسانی ارزش سهام اپل، به‌روزرسانی ارزش سهام گوگل، به‌روزرسانی ارزش سهام مایکروسافت، محاسبه سود.

این مسئله را می‌توانیم به صورت زیر نشان دهیم.

نکته کلیدی که می‌خواهیم به آن اشاره کنیم، درک علت تنظیم ماتریسی به شکل فوق است و نه توجه صرف به اعداد و ارقام. در ادامه این سناریو را بیشتر بررسی می‌کنیم.

فرض می‌کنیم اپل محصول جدیدی ارائه کرده است، بدین ترتیب سهام اپل 20 درصد افزایش داشته، سهام گوگل 5 درصد کاهش یافته و سهام مایکروسافت بدون تغییر مانده است. می‌خواهیم ارزش سهام را با استفاده از چیزی مانند ماتریس همانی اصلاح کنیم:

New Apple [1.2 0 0]

New Google [0 0.95 0]

New Microsoft [0 0 1]

ارزش جدید سهام اپل مقدار اولیه با افزایشی 20 درصد است (گوگل 5 درصد کاهش و مایکروسافت بدون تغییر). همچنین باید سود کلی را محاسبه کنیم.

تغییرات کلی:

(.20 * Apple) + (-.05 * Google) + (0 * Microsoft)

ماتریس عملیات نهایی به صورت زیر خواهد بود:

New Apple [1.2 0 0]

New Google [0 0.95 0]

New Microsoft [0 0 1]

Total Profit [.20 -.05 0]

در ماتریس فوق سه ورودی و چهار خروجی داریم. سه عملیات نخست یک «کپی اصلاح شده» و عملیات آخر، مجموع تغییرات است.

اینک مقدار ارزش سهام اولیه یک آلیس را به صورت (1000, 1000, 1000) و مقدار ارزش سهام اولیه باب را به صورت (500, 2000, 500) وارد می‌کنیم. می‌توانیم مقدار خروجی را به صورت دستی و یا به کمک محاسبات وب‌سایت ولفرم آلفا به دست آوریم.

توجه کنید که ورودی‌ها باید به صورت ستونی باشند؛ اما تایپ کردن آن‌ها به صورت ردیف راحت‌تر است. عملیات ترانهاده یا Transpose که با t مشخص شده است جای ردیف‌ها و ستون‌ها را به هم عوض می‌کند.

اعداد نهایی به این صورت هستند: آلیس 1200 دلار در سهام AAPL و ۹۵۰ دلار در سهام GOOG و ۱۰۰۰ دلار در سهام MSFT با سود خالص ۱۵۰ دلار دارد. باب نیز ۶۰۰ دلار در سهام AAPL و ۱۹۰۰ دلار در سهام GOOG و ۵۰۰ دلار در سهام MSFT با سود خالص ۰ دلار دارد.

می‌بینید که برای محاسبات خود از جبر خطی استفاده کردیم. جبر خطی در حدود سال 1800 معرفی شده است، اما صفحه‌های گسترده در دهه 1980 ظهور یافته‌اند. بنابراین، این ضعف آموزش جبر خطی است که موجب ناشناخته ماندن آن شده است.

نکات تاریخی: حل کردن معادلات همزمان

یکی از نخستین استفاده‌ها از جداول اعداد (در آن زمان هنوز مفهوم ماتریس معرفی نشده بود) حسابداری با استفاده از سیستم‌های خطی بوده است:

فرم ماتریسی معادلات بالا به صورت زیر است:‌

برای سهولت کار می‌توان به جای نوشتن کامل معادلات، صرفاً مقادیر ورودی و خروجی را در ماتریس‌های مربوطه وارد کرد. با ضرب ماتریس در ماتریس همانی مقادیر y ،x و z در سمت خروجی ظاهر می‌شوند.

این فرایند، فرایند حذف گاوس-جوردن (Gauss-Jordan) نامیده می‌شود و موجب صرفه‌جویی زمانی می‌شود. با این حال، جبر خطی به طور عمده به تبدیل‌های ماتریسی مربوط است و نه حل مجموعه معادلات و شما می‌توانید از اکسل برای محاسبه هزینه‌های فهرست خرید خود استفاده کنید.

اصطلاح‌شناسی، دترمینان‌ها و ویژه‌مقدارها

کلمه‌ها در دسته‌بندی‌های تکنیکی مانند (اسم، فعل، صفت) قرار می‌گیرند. ماتریس‌ها را نیز می‌توان به صورت مشابهی دسته‌بندی کرد. توصیف‌هایی مانند «بالا-مثلثی» «متقارن» یا «قطری»، شکل‌هایی از ماتریس هستند و بر تبدیل‌های آن‌ها تأثیر می‌گذارند.

فیلم آموزش ماتریس ها و جبر خطی – حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

دترمینان «اندازه» تبدیل خروجی است. اگر ورودی یک بردار واحد باشد (منظور از واحد، مساحت یا حجم 1 است) در این صورت دترمینان، اندازه مساحت تبدیل شده یا حجم تبدیل شده را نمایش می‌دهد. دترمینان صفر به این معنی است که ماتریس از نوع «مخرب» است و نمی‌تواند معکوس شود (مانند وضعیت ضرب در صفر که اطلاعات از بین می‌رود).

ویژه‌بردار و ویژه‌مقدارها نشان دهنده «محورهای» تبدیل هستند. برای مثال گردش یک کُره را در نظر بگیرید، هر مکانی با یک جهت جدید مواجه می‌شود، به جز نقاط قطبی.

یک «ویژه‌بردار» نوعی ورودی است که وقتی وارد ماتریس می‌شود، تغییری در جهت ایجاد نمی‌کند (یعنی در راستای محور است). با اینکه جهت‌گیری تغییری پیدا نمی‌کند، اما ممکن است اندازه تغییر یابد. ویژه‌مقدار به اندازه‌ای گفته می‌شود که ویژه‌بردار وقتی وارد ماتریس می‌شود تغییر می‌کند. برای اینکه تصویر واضح‌تری از این وضعیت داشته باشید، به تصویر زیر توجه کنید.

ماتریس‌ها و ورودی‌ها

شاید تا به اینجا از خود پرسیده باشید که آیا می‌توانیم با ماتریس عملیات نیز مانند یک ماتریس ورودی برخورد کنیم؟ برای اینکه بهتر متوجه شوید، برای مثال، یک دستور آشپزی را مانند فهرستی از دستورات در نظر بگیرید: دو فنجان شکر اضافه کنید، 3 فنجان آرد بیفزایید و غیره.

چه می‌شود اگر بخواهیم نسخه واحدی داشته باشیم؟ دستورالعمل‌ها را بگیریم و با آن‌ها مانند متن برخورد کنیم و آن‌ها را به واحدها تبدیل کنیم. دستور آشپزی «ورودی» است که می‌خواهیم تغییر دهیم و وقتی این کار را انجام دادیم، مجدداً می‌توانیم از دستورالعمل‌ها پیروی کنیم.

ماتریس عملیات نیز وضعیت مشابهی دارد و دستوراتی برای ایجاد تغییر است. با استفاده از ماتریس عملیات بر روی یک ماتریس دیگر یک ماتریس عملیات دیگر به دست می‌آید که شامل هر دو تبدیل است.

فرض کنید N به صورت «تغییر سبد سهام بر اساس اخبار» و T «تغییر سبد سهام بر اساس مالیات» باشد، در این صورت اگر هر دوی آن‌ها را اعمال کنی، داریم:

TN = X

یعنی ماتریس X را تولید کن که ابتدا بر اساس اخبار و سپس بر اساس مالیات تعدیل شده است. در این وضعیت، ما به هیچ سبد سهام ورودی نیاز نداریم و یک ماتریس را به صورت مستقیم روی ماتریس دیگر استفاده می‌کنیم.

زیبایی جبر خطی این است که کل محاسبات یک صفحه گسترده را صرفاً با یک حرف نشان می‌دهد. اگر بخواهیم تبدیل‌ها را چند بار اجرا کنیم کافی است از $$N^2$$ یا $$N^3$$ استفاده کنیم.

آیا می‌توانیم از جمع معمولی استفاده کنیم؟

قبلاً در بخش محاسبات خود بیان کردیم که صرفاً از ضرب می‌توانیم استفاده کنیم؛ اما اکنون می‌خواهیم کمی دید خود را وسعت بخشیم. تصور کنید یک آرگومان ساختگی 1 در ورودی خود ایجاد کنیم، به صورتی که (x, y, z) به صورت (x, y, z, 1) در آید.

اینک ماتریس عملیات ما یک عنصر اضافی دارد که می‌توانیم از آن استفاده کنیم. اگر بخواهیم x+1 را داشته باشیم، می‌توانیم بنویسیم:

[1 0 0 1]

و x + y – 3 به صورت زیر خواهد بود:

[1 1 0 -3]

با این کار، ما وانمود می‌کنیم که ورودی ما در یک بُعد بالاتر قرار دارد و یک «1» اضافی در آن بُعد قرار می‌دهیم. سپس آن بُعد بالاتر را اُریب (skew) می‌کنیم که مانند یک انحراف در بعد کنونی به نظر می‌آید. برای مثال فرض کنید (x, y, z, 1) را داریم و آن را روی ماتریس زیر اعمال می‌کنیم:

[1 0 0 1]

[0 1 0 1]

[0 0 1 1]

[0 0 0 1]

نتیجه به صورت (x + 1, y + 1, z + 1, 1) خواهد بود. با صرف‌نظر از بُعد چهارم، به همه ورودی‌ها یک مقدار «1» اضافه شده است. می‌توانیم آن آرگومان ساختگی را نگه داریم و در ادامه کارهای بیشتری با آن انجام دهیم. در نهایت، می‌بینیم که محاسبات کوچک ما دیگر محدود نیستند.

سخن پایانی

در این آموزش، برخی از مباحث جبر خطی را عامدانه بررسی نکردیم، زیرا مباحث مطرح شده در این آموزش کاربردی‌تر بوده و دیدی عمیق‌تر از جبر خطی به ما بخشیده‌اند. اینک می‌توانیم درک کنیم که چرا جبر خطی مفید است و این که چرا صفحه‌های گسترده مهم هستند.

از جبر خطی می‌توان برای حل تقریباً همه مسائل روزمره کمک گرفت. می‌توانید از یک تاجر بپرسید که دوست دارد یک کلیه‌اش را از دست بدهد یا برای همیشه از استفاده از صفحه گسترده محروم شود؟! یکی از مهم‌ترین نکاتی که در مورد جبر خطی می‌توان گفت، این است که جبر خطی نمادگذاری کارآمدی است که صفحه‌های گسترده را وارد معادلات ریاضی می‌کند.

==