قضیه رول (Rolle’s Theorem) — از صفر تا صد
در آموزشهای قبلی از مجموعه مطالب ریاضیات مجله فرادرس، درباره قضیه مقدار میانگین بحث کردیم. در آموزش مذکور، به قضیه رول نیز اشاره کردیم. در این آموزش، قضیه رول را به طور کامل معرفی خواهیم کرد.
قضیه رول
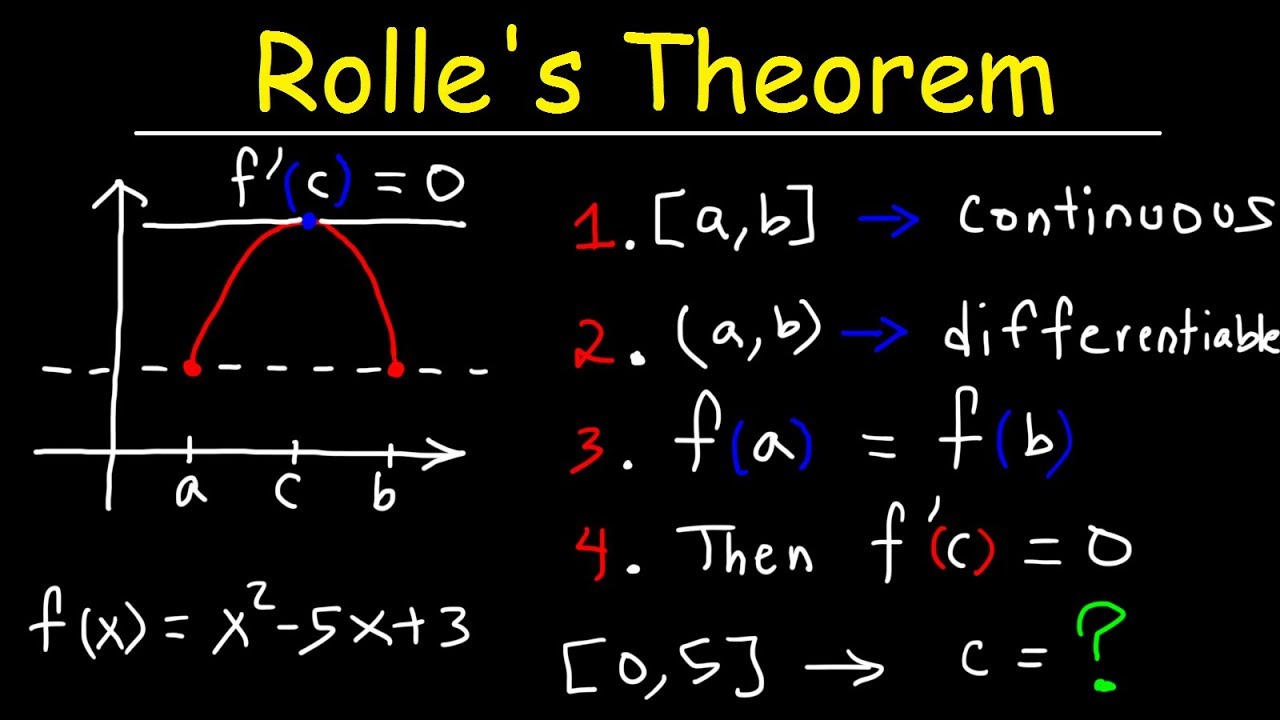
قضیه رول بیان میکند که هر تابع مشتقپذیر حقیقی که دارای مقادیر برابر برای نقاط ابتدا و انتهای یک بازه باشد، حداقل یک نقطه مانا (نقطهای که مشتق اول در آن صفر است) در بازه مذکور خواهد داشت.
از دیدگاه هندسی، خط مماس بر منحنی در این نقطه مانا، افقی است (شکل ۱).
این ویژگی، در قرن دوازدهم و در هند باستان شناخته شده بود. ستارهشناس و ریاضیدان مشهور هندی، باسکارا دوم (Bhāskara II) در نوشتههایش به این موضوع اشاره کرده بود.
فرم دقیق قضیه رول در سال ۱۶۹۱ توسط ریاضیدان فرانسوی، مایکل رول (Michel Rolle) اثبات شد (شکل ۲).

در ریاضیات مدرن، اثبات قضیه رول بر اساس دو قضیه دیگر، یعنی قضیه مقدار اکسترمم وایرشتراس و قضیه فرما است. بیان دو قضیه در ادامه آمده است.
قضیه مقدار اکسترمم وایرشتراس
اگر تابع $$ f ( x ) $$ در بازه بسته $$ \left[ {a,b} \right] $$ پیوسته باشد، آنگاه به کوچکترین کران بالا و بزرگترین کران پایین در این بازه میرسد.
قضیه فرما
فرض کنید تابع $$ f (x)$$ در همسایگی نقطه $$ x _ 0 $$ تعریف شده و در این نقطه مشتقپذیر باشد. در نتیجه اگر تابع $$ f (x) $$ یک اکسترمم محلی در $$ x _0 $$ داشته باشد، آنگاه داریم:
$$ \large f ’ \left ( { { x _ 0 } } \right ) = 0 . $$
اکنون قضیه رول را دقیقتر بیان میکنیم. فرض کنید تابع $$ y = f\left( x \right) $$ در بازه بسته $$ \left[ {a,b} \right] $$ پیوسته و در بازه باز $$ \left( {a,b} \right) $$ مشتقپذیر بوده و مقدار آن برای نقاط ابتدا و انتهای بازه برابر باشد:
$$ \large f \left ( a \right ) = f \left ( b \right ) . $$
آنگاه، روی بازه $$ \left( {a,b} \right) $$ حداقل یک نقطه $$ \xi \in \left( {a,b} \right) $$ وجود دارد که به ازای آن، مشتق تابع $$ f (x ) $$ برابر با صفر است:
$$ \large f ’ \left ( \xi \right ) = 0 . $$
اثبات قضیه رول
ابتدا فرض میکنیم تابع $$ f (x) $$ روی بازه $$ \left[ {a,b} \right] $$ ثابت باشد. در نتیجه، مشتق آن در هر نقطه از بازه $$ \left( {a,b} \right) $$ برابر با صفر خواهد بود؛ یعنی در این حالت حکم درست است.
حال فرض میکنیم تابع $$ f (x) $$ روی بازه $$ \left[ {a,b} \right] $$ ثابت نباشد. در این حالت، طبق قضیه مقدار اکسترمم وایرشتراس، تابع به بزرگترین یا کوچکترین مقدار در نقطه $$ \xi $$ از بازه $$ \left( {a,b} \right) $$ میرسد. طبق قضیه فرما نیز مشتق در این نقطه صفر است:
$$ \large f ’ \left ( \xi \right ) = 0 . $$
قضیه رول یک تعبیر فیزیکی واضح دارد؛ فرض کنید جسمی در طول یک خط راست حرکت میکند و بعد از یک دوره زمانی مشخص به نقطه شروع بر میگردد. در این دوره زمانی، لحظهای وجود خواهد داشت که در آن، سرعت لحظهای جسم به صفر میرسد.
مثالها
در این بخش مثالهایی را درباره قضیه رول بیان میکنیم.
مثال ۱
ثابت کنید اگر معادله
$$ \large f { \left ( x \right ) = { a _ 0 } { x ^ n } + { a _ 1 } { x ^ { n – 1 } } + \ldots } \kern0pt { \; + \; { a _ { n – 1 } } x = 0 \; \; \; } $$
دارای یک ریشه مثبت $$ x = {x_0} $$ باشد، آنگاه معادله
$$ \large n { a _ 0 } { x ^ { n – 1 } } + \left ( { n – 1 } \right ){ a _ 1 } { x ^ { n – 2 } } + \ldots + { a _ { n – 1 } } = 0 $$
نیز یک ریشه مثبت $$ x = \xi $$ دارد که $$ \xi \lt {x_0} $$ است.
حل: علاوه بر $$ x = {x_0} $$، معادله نخست دارای ریشه $$ x = 0 $$ نیز هست. در نتیجه، تابع $$ f (x) $$ در شرایط قضیه رول صدق میکند:
$$ \large f \left ( 0 \right ) = f \left ( { { x _ 0 } } \right ) = 0 . $$
معادله دوم با مشتقگیری از معادله اول به دست میآید:
$$ \large \begin{align*}
f ’ \left ( x \right ) & = { { \left ( { { a _0 } { x ^ n } + { a _ 1 }{ x ^ { n – 1 } } + \ldots + { a _ { n – 1 } } x } \right ) ^ \prime } } \\ & = { n { a _ 0 } { x ^ { n – 1 } } + \left ( { n – 1 } \right ){ a _ 1 } { x ^ { n – 2 } } + \ldots + { a_ { n – 1 } } = 0 . }
\end{align*} $$
طبق قضیه رول، یک نقطه درونی $$ x = \xi $$ در بازه $$ \left[ {0,{x_0}} \right] $$ وجود دارد که مشتق در آنجا صفر است. در نتیجه، $$ x = \xi $$ یک جواب برای معادله دوم است که در رابطه $$ 0 \lt \xi \lt {x_0} $$ صدق میکند.
مثال ۲
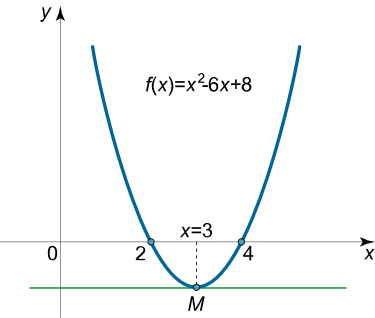
اعتبار قضیه رول را برای تابع زیر بررسی کنید:
$$ \large f \left ( x \right ) = { x ^ 2 } – 6 x + 8 . $$
حل: تابع درجه دوم بالا، دو ریشه $$ x = 2 $$ و $$ x = 4 $$ دارد:
$$ \large f \left ( 2 \right ) = f \left ( { 4 } \right ) = 0 . $$
طبق قضیه رول، یک نقطه $$ \xi $$ در بازه $$ \left( {2,4} \right) $$ وجود دارد که در آن، مشتق تابع $$ f (x) $$ برابر با صفر است.
$$ \large f ’ \left ( x \right ) = { \left ( { { x ^ 2 } – 6 x + 8 } \right ) ^ \prime } = 2 x – 6. $$
مشتق اخیر در نقطه $$ x = \xi $$ برابر با صفر است:
$$ \large { f ’ \left ( x \right ) = 0 , \; \; } \Rightarrow { 2 x – 6 = 0 , \; \; } \Rightarrow { x = \xi = 3 . } $$
میبینیم که نقطه مانای $$ \xi = 3 $$ در بازه $$ \left( {2,4} \right) $$ قرار دارد (شکل ۳).
مثال ۳
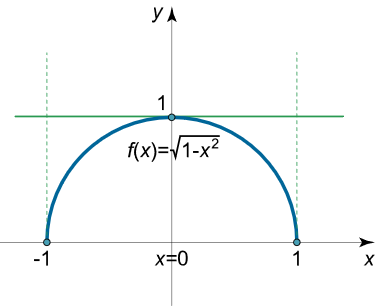
اعتبار قضیه رول را برای تابعِ
$$ \large f \left ( x \right ) = \sqrt {{ 1 – { x ^ 2 }} } $$
روی بازه $$ \left[ { – 1,1} \right] $$ بررسی کنید.
حل: ابتدا بررسی میکنیم که تابع در ابتدا و انتهای بازه مقدار یکسانی داشته باشد:
$$ \large f \left ( { - 1 } \right ) = f \left ( { 1 } \right ) = 0 . $$
بنابراین، مشتق در نقطهای از $$ \xi \in \left( { – 1,1} \right) $$ باید برابر با صفر باشد.
مشتق تابع برابر است با:
$$ \large \begin{align*}
\require {cancel} f ’ \left ( x \right ) & = { \left ( { \sqrt { 1 – { x ^ 2 } } } \right ) ^ \prime } = { \frac { 1 } { { 2 \sqrt { 1 – { x ^ 2 } } } } \cdot { \left ( { 1 – { x ^ 2 } } \right ) ^ \prime } } \\ & = { \frac { { – \cancel { 2 } x } } { { \cancel { 2 } \sqrt { 1 – { x ^ 2 } } } } } = { - \frac { x } { { \sqrt { 1 – { x ^ 2 } } } } . }
\end{align*} $$
مشتق در نقطه $$ x = 0 $$، صفر است. بنابراین، $$ \xi = 0 $$ خواهد بود.
دقت کنید که این تابع، نیمدایره بالایی با شعاع $$ R= 1 $$ را مشخص میکند که مرکز آن در مبدأ مختصات است (شکل ۴). در نقاط ابتدا و انتهای بازه $$ \left[ { – 1,1} \right] $$، مشتق محدود وجود ندارد؛ یعنی این تابع در $$ x = \pm 1 $$ مشتقپذیر نیست. با وجود این، قضیه رول برقرار است، زیرا تابع باید در بازه باز $$ \left( { – 1,1} \right) $$ مشتقپذیر باشد.
مثال ۴
قضیه رول را برای تابع زیر در بازه $$ \left[ {1,3} \right] $$ بررسی کنید:
$$ \large
f \left ( x \right ) = \frac { { { x ^ 2 } – 4 x + 3 } } { { x – 2 } }
$$
حل: ابتدا برابر بودن مقدار تابع را در ابتدا و انتهای بازه بررسی میکنیم:
$$ \large { f \left ( 1 \right ) = \frac { { { 1 ^ 2 } – 4 \cdot 1 + 3 } } { { 1 – 2 } } = 0 , } \; \; \; \kern-0.3pt { f \left ( 3 \right ) = \frac { { { 3 ^ 2 } – 4 \cdot 3 + 3 } } { { 3 – 2 } } = 0 . } $$
البته در $$ x = 2 $$ یک ناپیوستگی وجود دارد؛ یعنی یکی از سه شرط قضیه رول (شرط پیوستگی تابع در بازه $$ \left[ {a,b} \right] $$) برقرار نیست.
بنابراین، در این مثال نمیتوان از قضیه رول استفاده کرد.
مثال ۵
اعتبار قضیه رول را برای تابع زیر در بازه $$ \left[ {0,2} \right] $$ بررسی کنید:
$$ \large f \left ( x \right ) = \left | { x – 1 } \right | $$
حل: این تابع در بازه $$ \left[ {0,2} \right] $$ پیوسته است و مقادیر آن در ابتدا و انتهای بازه با هم برابرند:
$$ \large { f \left ( 0 \right ) = \left | { 0 – 1 } \right | = \left | { – 1 } \right | = 1 , } \; \; \; \kern-0.3pt { f \left ( 2 \right ) = \left | { 2 – 1 } \right | = \left | 1 \right | = 1 . } $$
شرط سوم قضیه رول (لزوم مشتقپذیر بودن تابع در بازه باز $$ \left( {0,2} \right) $$) برقرار نیست، زیرا مشتق در $$ x = 1 $$ وجود ندارد (در این نقطه، تابع یک نقطه بازگشت دارد).
مثال ۶
تعداد نقاط مانای تابع زیر را به دست آورید:
$$ \large f \left ( x \right ) = x \left ( { x – 1 } \right ) \left ( { x – 2 } \right ) $$
همچنین بازههایی را که این نقاط در آن واقع شدهاند، تعیین کنید.
حل: مقدار تابع در نقاط زیر صفر میشود:
$$ \large { { x _ 1 } = 0 , } \; \; \; \kern-0.3pt { { x _ 2 } = 1 , } \; \; \; \kern-0.3pt { { x _ 3 } = 2 . } $$
دو بازه $$ \left[ {0,1} \right] $$ و $$ \left[ {1,2} \right] $$ را در نظر بگیرید. واضح است که شرایط قضیه رول در هر یک از این بازهها صدق میکنند. بنابراین، دو نقطه مانای $$ {\xi_1} $$ و $$ {\xi_2} $$ در بازههای زیر وجود دارند:
$$ \large { { \xi _ 1 } \in \left ( { 0 , 1 } \right ) , } \; \; \;\kern-0.3pt { { \xi _ 2 } \in \left ( { 1 , 2 } \right ) . } $$
برای تأیید این نتیجهگیری، مشتق را به دست آورده و نقاط مانا را محاسبه میکنیم:
$$ \large \begin{align*}
f \left ( x \right ) & = x \left ( { x – 1 } \right ) \left ( { x – 2 } \right ) = { \left ( { { x ^ 2 } – x } \right ) \left ( { x – 2 } \right ) } \\ & = { { x ^ 3 } – { x ^ 2 } – 2 { x ^ 2 } + 2 x } = { { x ^ 3 } – 3 { x ^ 2 } + 2 x; }
\end {align*}
$$
$$ \large { f ’ \left ( x \right ) } = { { \left ( { { x ^ 3 } – 3 { x ^ 2 } + 2 x } \right ) ^ \prime } } = { 3 { x ^ 2 } – 6 x + 2 . } $$
ریشههای مشتق به صورت زیر به دست میآیند:
$$ \large \begin{align*}
f ’ \left ( x \right ) & = 0 , \; \; \Rightarrow { 3 { x ^ 2 } – 6 x + 2 = 0 , \; \; } \Rightarrow { D = 3 6 – 4 \cdot 3 \cdot 2 = 1 2 , \; \; } \\ & \Rightarrow { { x _ { 1 , 2 } } = \frac { { 6 \pm \sqrt { 1 2 } } } { 6 } } = { 1 \pm \frac { 1 } { { \sqrt 3 } } \approx 0 . 4 2 ; \; 1.58.}
\end {align*}
$$
بنابراین، نقطه مانای اول $$ {x_1} \approx 0.42 $$ در بازه $$ \left( {0,1} \right) $$ و نقطه دوم $$ {x_2} \approx 1.58 $$ در بازه $$ \left( {1,2} \right) $$ صدق میکنند.
مثال ۷
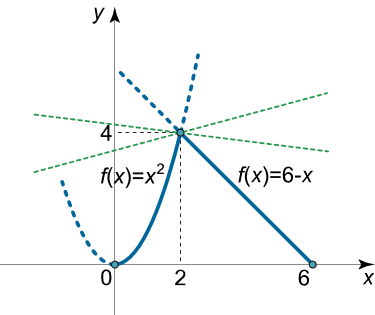
اعتبار قضیه رول را برای تابع زیر بررسی کنید:
$$ \large f ( x ) =
\begin {cases}
x ^ 2 & \text {,} \; \; \; 0 \le x \le 2 \\
6 - x & \text{,} \; \; \; 2 \lt x \le 6
\end{cases}. $$
حل: تابع در بازه $$ \left[ {0,6} \right] $$ پیوسته بوده و مقدار آن در ابتدا و انتهای این بازه با هم برابر است:
$$ \large { f \left ( 0 \right ) = { 0 ^ 2 } = 0 , } \; \; \; \kern-0.3pt { f \left ( 6 \right ) = 6 – 6 = 0 . } $$
البته این تابع در $$ x = 2 $$ مشتقپذیر نیست. در واقع، وقتی مشتق را در این نقطه محاسبه میکنیم، نتیجه به علامت نمُو $$ \Delta x $$ بستگی دارد:
اگر $$ \Delta x < 0 $$، آنگاه داریم:
$$ \large \begin{align*}
f ’ \left ( x \right ) & = \lim \limits _ { \Delta x \to 0 } \frac { { f \left ( { x + \Delta x } \right ) – f \left ( x \right ) } } { { \Delta x } } = { \lim \limits _ { \Delta x \to 0 } \frac { { { { \left ( { x + \Delta x } \right ) } ^ 2 } – { x ^ 2 } } } { { \Delta x } } } \\ & = { \lim \limits _ { \Delta x \to 0 } \frac { { \cancel { x ^ 2 } + 2 x \Delta x + { { \left ( { \Delta x } \right ) } ^ 2 } – \cancel { x ^ 2 } } } { { \Delta x } } } \\ & = { \lim \limits _ { \Delta x \to 0 } \left ( { 2 x + \Delta x } \right ) = 2 x , \; \; } \Rightarrow { f ’ \left ( { 2 – 0 } \right ) = 4 . }
\end {align*}
$$
برای $$ \Delta x > 0 $$ نیز رابطه زیر به دست میآید:
$$ \large \begin{align*}
f ’ \left ( x \right) & = \lim \limits _ { \Delta x \to 0 } \frac { { f \left ( { x + \Delta x } \right ) – f \left ( x \right ) } } { { \Delta x } } = { \lim \limits _ { \Delta x \to 0 } \frac { { \left [ { 6 – \left ( { x + \Delta x } \right ) } \right ] – \left ( { 6 – x } \right ) } } { { \Delta x } } } \\ & = { \lim \limits _ { \Delta x \to 0 } \frac { { \cancel { 6 } – \cancel { x } – \Delta x – \cancel { 6 } + \cancel { x } } } { { \Delta x } } } \\ & = { \lim \limits _ { \Delta x \to 0 } \left ( { – \frac { { \cancel { \Delta x } } } { { \cancel { \Delta x } } } } \right ) = – 1 , \; \; } \Rightarrow { f ’ \left ( { 2 + 0 } \right ) = – 1 . }
\end {align*}
$$
روابط بالا بدین معنی است که مشتق در نقطه $$ x = 2 $$ وجود ندارد (شکل ۵) و در نتیجه، شرط مشتقپذیری تابع در تمام نقاط بازه برقرار نیست. بنابراین، قضیه رول در اینجا صدق نمیکند.
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
^^











خیلی عالی بود😍واقعا ممنونتونم🫶
سلام بسیار ممنون و متشکر از مطالب که با بیانی واصح و مثالهایی روان به تفهیم قضایا پرداخته اید. موفق باشید انشاءالله