دامنه و برد تابع — به زبان ساده

به صورت ساده میتوان بیان کرد که دامنه یک تابع، شامل تمام مقادیری است که به عنوان ورودی به تابع داده میشوند و برد تابع نیز مجموعه مقادیر خروجی از تابع را در بر میگیرد. این موضوع، یعنی مفهوم دامنه و برد تابع به سادگی در شکل زیر نشان داده شده است.
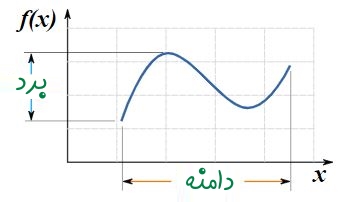
اما مهمترین نکتهای که باید به آن توجه کنید این است که دامنه و برد، دو مفهوم اساسی در تعریف توابع هستند و با تغییر آنها تعریف تابع نیز تغییر میکند. در ادامه این مطلب از مجله فرادرس، این موضوع به صورت دقیق مورد بررسی قرار میگیرد و تعریف جامعی از دامنه، برد و همدامنه ارائه میشود.
توابع
همانطور که میدانید، یک تابع روی مجموعهای از ورودیها عمل میکند و مجموعهای از خروجیها را تولید میکند.
بنابراین میتوان بیان کرد که هر تابع از یک سری ورودی و خروجی تشکیل شده است. برای آنکه مفهوم این موضوع را به صورت دقیق متوجه شوید، به مثال زیر توجه کنید.
مثال
درختی که در شکل زیر نشان داده شده است هر سال به اندازه ۲۰ سانتی متر رشد میکند.

بنابراین میتوان بیان کرد که ارتفاع درخت به میزان سن آن با استفاده از تابع h مرتبط است. این تابع را میتوان به شکل زیر نمایش داد.
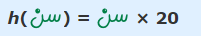
بنابراین در صورتی که سن درخت برابر با 10 سال باشد، ارتفاع آن مطابق با رابطه زیر، برابر با 200 سانتی متر خواهد بود.
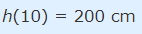
رابطه فوق را میتوان اینگونه بیان کرد که تابع h، عدد 10 را به 200 تبدیل کرده است. بنابراین عدد 10 ورودی این تابع و 200 خروجی آن را نشان میدهد. این موضوع با استفاده از رابطه زیر نیز به خوبی نشان داده شده است.
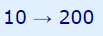
ورودی و خروجی یک تابع
نکته بسیار مهمی که باید به آن توجه کنید این است که، تمامی مقادیر و اعداد را نمیتوان به عنوان ورودی به تابع معرفی کرد و اگر به تابع ورودی اشتباه بدهیم، ممکن است که تابع عمل نکند و هیچ خروجی را به ما تحویل ندهد.
دانستن اطلاعات کلی درمورد خروجیهای تابع نیز امر بسیار مهمی است. برای مثال اگر بدانیم که این تابع تنها مقادیر مثبت را به عنوان خروجی به ما تحویل میدهد، درک مسئله برای ما بسیار سادهتر خواهد بود.
علاوه بر موارد ذکر شده، میتوان بیان کرد که یک تابع، روی مجموعههای مشخصی عمل میکند. در ادامه برخی از این مجموعهها را مورد مطالعه قرار میدهیم.
به عنوان مثال اول، مجموعه تمام اعداد زوج (مثبت و منفی) را میتوان با استفاده از مجموعه اعداد زیر نمایش داد.

مشابه مثال بالا میتوان مجموعه اعداد صحیح فرد را نیز به شکل زیر نمایش داد.
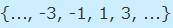
در ادامه مجموعهای شامل تمام اعداد اول را مورد بررسی قرار میدهیم. توجه کنید که عدد اول، یک عدد طبیعی بزرگتر از یک است که به هیچ عددی به غیر از یک و خود آن عدد، بخش پذیر نیست. مجموعه این اعداد در رابطه زیر نشان داده شده است.
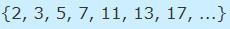
علاوه بر موارد ذکر شده، مجموعهها را میتوان به اعداد طبیعی، صحیح و گویا نیز محدود کرد. به غیر از مجموعههای کلی که در بالا اشاره شد، امکان دارد مجموعههای دلخواهی نیز در توابع به عنوان ورودی یا خروجی تعریف شوند. برای مثال ممکن است ورودی یک تابع تنها شامل اعداد مثبت کوچکتر از ۱۰ و مضرب ۳ باشد. این مجموعه دلخواه را به شکل زیر نمایش میدهند.

به صورت کلی میتوان بیان کرد که یک تابع، هرکدام از اعضای یک مجموعه را دقیقا به یکی از اعضای مجموعه دیگر مرتبط میکند. توجه کنید که ممکن است دو مقدار از مجموعه اول (دامنه) به یک مقدار از مجموعه دوم (برد) منتقل شوند.
نکته مهم دیگر این است که اگر یک مقدار از مجموعه اول (دامنه) به دو مقدار از مجموعه دوم (برد)، مرتبط شود، با تعرف تابع در تضاد است و این عملگر را نمیتوان تابع نامید. تعریف تابع و مجموعه دامنه و برد در شکل زیر به خوبی نشان داده شده است.
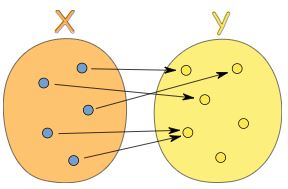
دامنه و برد چیست
دامنه یک تابع، مجموعهای است که به عنوان ورودی تابع در نظر گرفته میشود و برد تابع، مجموعهای است که تمامی خروجیهای تابع را در بر میگیرد.
مجموعه دیگری نیز تحت عنوان همدامنه در تعریف تابع حضور دارد. همدامنه شامل مجموعهای از اعداد است که خروجی تابع میتواند جزئی از آنها باشد. همدامنه را دامنه مشترک نیز مینامند. برای مشخص شدن مفهوم این تعاریف به مثال زیر توجه کنید.
مثال
تابعی با رابطه زیر را در نظر بگیرید.

این تابع مانند شکل زیر بین مجموعههای A و B عمل میکند و هر عضو مجموعه A را به یک عضو مجموعه B مرتبط میسازد.
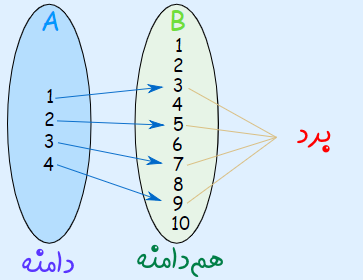
بنابراین مجموعه A، دامنه تابع را نمایش میدهد و مجموعه B، همدامنه را مشخص میکند. توجه کنید که همدامنه را معمولا صورت مسئله تعیین میکند و برد، زیر مجموعهای از این همدامنه است.
در این مثال، برد تابع، مجموعهای است که اعداد 3، 5، 7 و 9 را شامل میشود. برد این تابع زیر مجموعهای از همدامنه (مجموعه B) است. این سه مجموعه یعنی دامنه، همدامنه و برد را میتوان به کمک مجموعههای زیر هم نمایش داد.
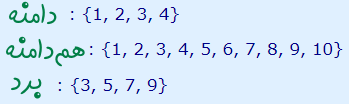
اجزای مختلف یک تابع
در تعریف تابع، دامنه و برد نشان دادیم که آنچه که از تابع بیرون میآید (برد تابع) وابستگی مستقیم به ورودی تابع (دامنه تابع) دارد. بنابراین میتوان بیان کرد که یکی از مهمترین بخشهای تابع، دامنه آن است و تغییر دامنه باعث تغییر خروجی تابع و ویژگیهای مختلف آن تابع میشود.
برای مشخص شدن مفهوم این قضیه به مثال زیر توجه کنید.
مثال
تابع سادهای را که رابطه آن به فرم است را در نظر بگیرید. دامنه این تابع یعنی آنچه به عنوان ورودی به تابع داده میشود را میتوانیم مجموعهای شامل اعداد طبیعی به فرم تعریف کنیم. با استفاده از این دامنه و رابطه تابع، برد تابع به فرم مجموعه زیر در میآید.
این تابع با استفاده از دامنه و بردی که در بالا تعریف شد، به صورت زیر مشخص میشود.
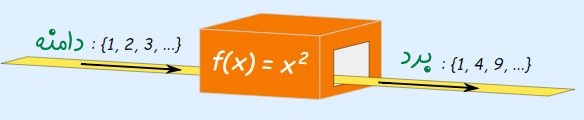
حال تابع دیگری که رابطه مشابهی با تابع قبلی دارد را در نظر بگیرید. ابن تابع را با حرف g و با استفاده از رابطه میتوان مشخص کرد. دامنه این تابع را به صورت مجموعه تمام اعداد صحیح به فرم زیر در نظر بگیرید.
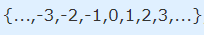
در این شرایط، برد تابع به شکل زیر در میآید.

توجه کنید که برد تابع جدید نسبت به حالت قبل یک عدد صفر (0) بیشتر دارد. این تابع، دامنه و برد آن را میتوان به شکل زیر نمایش داد.
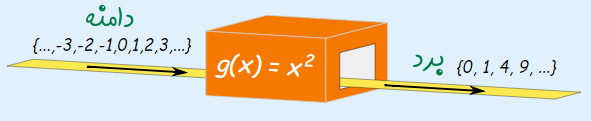
همانطور که مشاهده میشود، هر دو تابع مجذور ورودی را به عنوان خروجی تحویل میدهند ولی از آنجایی که این دو تابع ورودی و دامنه متفاوتی دارند، خروجی و برد آنها نیز متفاوت خواهد بود.
توجه کنید که خواص این دو تابع نیز متفاوت است. در حالت اول، تابع f، به صورت یک به یک است و به ازای هر ورودی یک خروجی را تولید میکند. این در حالی است که تابع g یک به یک نیست و به ازای دو ورودی مختلف، یک جواب یکسان را تولید میکند. این موضوع در دو رابطه زیر نشان داده شده است.
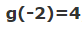
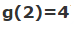
بنابراین با توجه به مثال و توضیحات بالا، میتوان نتیجه گرفت که یکی از بخشهای اساسی تابع، دامنه آن است. انواع مختلف دامنه میتواند ویژگیهای گوناگون تابع را تحت تاثیر خود قرار دهد.
محدودیتهای تعریف دامنه یک تابع
در قسمتهای قبل نشان داده شد که دامنه یک تابع و شیوه تعریف آن تاثیر مستقیمی روی ویژگیهای مختلف تابع دارد.
توجه کنید که تمامی مقادیر را نمیتوان به عنوان ورودی یک تابع در نظر گرفت. برای مثال در صورتی که تابعی به فرم داشته باشیم، دامنه تابع را باید از میان اعداد مثبت انتخاب کنیم تا عبارت زیر رادیکال مقداری مثبت داشته باشد. در این صورت برد این تابع در مجموعه اعداد حقیقی قرار میگیرد و در غیر این صورت، برد تابع مجموعه اعداد مختلط را نیز در بر خواهد گرفت.
بنابراین در تعریف دامنه توابع باید به صورت دقیق عمل کنیم. برای این منظور آشنایی با انواع اعداد و زیر مجموعههای مختلف اعداد حقیقی مانند اعداد گویا، امری ضروری است.
تفاوت برد و همدامنه
برد و همدامنه، دو تعریف بسیار مهم در توابع هستند و هر دو در قسمت خروجی تابع قرار میگیرند ولی دو تعریف مجزا و متفاوت دارند. در قسمت قبل نیز اشاره شد که همدامنه، مجموعهای است که خروجی و برد تابع را در بر میگیرد و در واقع برد یک تابع زیر مجموعهای از همدامنه آن تابع در نظر گرفته میشود.
نکته مهمی که باید به آن اشاره کرد این است که همدامنه بخشی از تعریف تابع است و در تعریف تابع، هنگام بیان رابطه و دامنه آن، همدامنه نیز معرفی میشود. این در حالی است که برد تابع، مقادیری را نشان میدهد که به صورت واقعی شامل تمام خروجیهای تابع هستند و از طریق انجام محاسبات مختلف به دست میآید. برای مشخص شدن دقیق تفاوت این دو مفهوم، به مثال زیر توجه کنید.
مثال
تابعی را به فرم در نظر بگیرید. دامنه و همدامنه این تابع به صورتی تعریف شده که تنها شامل اعداد صحیح هستند. توجه کنید که تعریف دامنه و همدامنه کاملا دست خود ما است و ما تعیین میکنیم که دامنه و همدامنه تابع شامل چه مقادیری باشند.

همانطور که از تعریف این تابع نتیجه میشود، زمانی که ورودی این تابع به صورت اعداد صحیح باشند، خروجی تابع تنها شامل اعداد صحیح زوج خواهد بود.
بنابراین همدامنه شامل تمام اعداد صحیح است و برد این تابع تنها اعداد صحیح زوج را در بر میگیرد.
مطابق با توضیحاتی که در بالا داده شد میتوان نتیجه گرفت که برد یک تابع، زیر مجموعهای از همدامنه آن است. اما دلیل اینکه از هر دو تعریف برای توابع مختلف استفاده میشود این است که گاهی تابع ما بسیار پیچیده است و ما به راحتی نمیتوانیم برد تابع را محاسبه کنیم. در این حالت با تعریف همدامنه و دامنه میتوانیم محدودهای که برد در آن قرار دارد را مشخص کنیم و با استفاده از این موضوع سایر محاسبات موجود در مسئله را ادامه میدهیم.
نماد ریاضی
دامنه، برد و همدامنه را در ریاضیات با استفاده از قراردادهایی معرفی میکنند که این قراردادها و نمادها در این بخش مورد مطالعه قرار میگیرند. برای مثال نماد زیر را در تعریف یک تابع در نظر بگیرید.
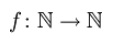
این نماد نشان میدهد که دامنه تابع f، شامل مجموعه اعداد طبیعی (N) است و همدامنه آن نیز مجموعه اعداد طبیعی (N) را در بر میگیرد. توجه شود که اعداد صحیح را با نماد Z و اعدا حقیقی را با نماد R نمایش میدهند. برای نشان دادن اعداد گویا نیز از نماد Q استفاده میشود.
بنابراین همانطور که نشان داده شد، هر تابع نیاز به داشتن یک دامنه، یک برد و یک همدامنه دارد. این سه مورد تعریف یک تابع را کامل میکنند.
این مطلب به صورت دقیق ابتدا به بررسی توابع مختلف پرداخت و ورودی و خروجی آنها را مورد ارزیابی قرار داد. در ادامه، دامنه، برد، همدامنه و اجزای مختلف تابع تعریف شدند. سپس محدودیتهایی که در تعریف یک تابع وجود دارد مورد بررسی قرار گرفت و تفاوت برد و همدامنه به خوبی شرح داده شد. در انتها نیز شیوه نمایش ریاضی این سه مفهوم یعنی برد، دامنه و همدامنه یک تابع مورد بررسی قرار گرفت.












بسیار عالی بود. سپاسگزارم
عالی بود مخصوصا قسمت هم دامنه
خیلی خوب توضیح دادین ممنون
عالی بود به خصوص قسمت هم دامنه خیلی خوب توضیح داده شد.
خیلی عالی بود استاد تعاریف و مقال هاتون عالی بود خدا خیرتون بده
عالی خیلی ممنون
بسیار عالی. ممنون
واقعا آموزش مفیدی بود
سپاس بی پایان
عالی بود خیلی ممنون
????
یک دنیا ممنون
سپاس گذارم،بسیارکامل وعالی
خیلی ممنون
سپاس گذارم،بسیار عالی بود
ممنون جالب بود
عالی بود ممنون?
خیلی عالی بود ممنون
عالی!!!!!!!!!!!!
ممنون مفید بود