حد یک طرفه و محاسبه آن – به زبان ساده

در مطالب قبلی وبلاگ فرادرس، با مفاهیم مختلف حد، مانند حد بینهایت و حد در بینهایت آشنا شدیم. همانطور که مشاهده می‌شود، یکی از مباحث بسیار مهم در ریاضیات، مبحث حد یک طرفه است و کاربرد بسیار زیادی در تعیین مقدار حد تابع در یک نقطه مشخص دارد.

این مطلب ابتدا به صورت دقیق به بررسی مفهوم حد یک طرفه و حدهای راست و چپ می‌پردازد و در ادامه به کمک چندین مثال، حالات مختلف مربوط به این نوع حد را مورد ارزیابی قرار می‌دهد.

حد یک طرفه چیست؟

یکی از مواردی که به صورت رایج در حدهای مختلف مشاهده می‌شود، این است که حد یک تابع در یک نقطه وجود ندارد و دلیل این موضوع می‌تواند موارد بسیار زیادی را شامل شود. برای مثال تابع زیر را در نظر بگیرید.

$${ \large \mathop { \lim } \limits _ { t \to 0 } \,\, \cos \left ( { \frac { \pi } { t } } \right) }$$

همانطور که مشاهده می‌شود، زمانی که متغیر این تابع یعنی $${ t }$$ به سمت صفر میل می‌کند، مقدار تابع به سمت عدد مشخصی میل نمی‌کند و تابع کسینوسی در محدود 1- تا 1 در حال نوسان است. بنابراین حد بیان شده در نقطه $${ t = 0 }$$ موجود نیست. در واقع زمانی حد تابع در یک نقطه موجود است که تابع مورد نظر در نقطه مشخص شده به سمت یک عدد واحد میل کند. برای مثال حد یک تابع پله را در نقطه $${ t = 0 }$$ در نظر بگیرید.

$${ \large \mathop { \lim } \limits _ {t \to 0 } H \left ( t \right ) }$$

رابطه این تابع پله را می‌توان به شکل زیر بیان کرد.

$$ { \large H \left ( t \right ) = \left \{ \begin {array} { l l } 0 & { \mbox { if } } t < 0 \\ 1 & { \mbox { if } } t \ge 0 \end {array} \right. } $$

همانطور که مشاهده می‌شود، زمانی که از مقادیر کمتر از صفر به $${ t = 0 }$$ نزدیک می‌شویم، مقدار تابع برابر با 0 و زمانی که از مقادیر بیشتر از 0 به $${ t = 0 }$$ نزدیک می‌شویم، مقدار تابع برابر با 1 خواهد بود. بنابراین این تابع در نقطه $${ t = 0 }$$ به سمت مقدار واحدی میل نمی‌کند و حد تابع در نقطه بیان شده، موجود نیست.

بر این اساس حد تابع پله بالا به این بستگی دارد که در کدام سمت از نقطه $${ t = 0 }$$ قرار داریم. بنابراین در اینگونه مسائل معمولا ما به دنبال یافتن «حدهای یک طرفه» (one-sided limits) هستیم. در واقع حد یک طرفه در یک نقطه، همانطور که از نام آن پیداست، نشان دهنده حد تابع در یکی از دو سمت (سمت راست یا سمت چپ) این نقطه است.

بنابراین همانطور که توضیح داده شد، حد یک طرفه به صورت کلی به دو دسته حد راست و حد چپ تقسیم می‌شود که در ادامه به بررسی تعریف ریاضی این دو نوع حد پرداخته می‌شود.

حد راست

همانطور که بیان شد یکی از حدهای یک طرفه، حد راست است که می‌توان آن را با استفاده از رابطه زیر به صورت ریاضی تعریف کرد.

$${ \large \mathop { \lim } \limits _ { x \to { a ^ + } } f \left ( x \right ) = L }$$

در واقع در این حالت به دنبال یافتن مقدار تابع $$f$$ در نقطه‌ای هستیم که از مقادیر بیشتر از a ($${ x > a }$$) به سمت $$a$$ میل می‌کند و هیچوقت برابر با $$a$$ ($$x \neq a$$) نیست.

حد چپ

به صورت مشابه می‌توان حد چپ تابع $${ f ( x ) }$$ در نقطه $${ x = a }$$ را نیز با استفاده از رابطه زیر تعریف کرد.

$${ \large \mathop { \lim } \limits _ { { x } \to { { a } ^ { - } } } { f } \left ( { x } \right ) = L }$$

در اینجا نیز به دنبال یافتن مقادیر تابع $$f$$ در نقطه‌ای هستیم که از مقادیر کمتر از a ($${ x < a }$$) به سمت $$a$$ میل می‌کند و هیچوقت برابر با $$a$$ ($$x \neq a$$) نیست. به این مقدار، حد چپ تابع $$f$$ در نقطه $${ x = a }$$ می‌گویند.

نکته بسیار مهمی که باید به آن توجه کنید این است که تفاوت نماد حد چپ و راست بسیار ناچیز است. در واقع حد راست با علامت مثبت (+) روی $${ x \to { a ^ + } }$$ نمایش داده می‌شود که به این معنا است که ما تنها به دنبال اعدادی در ناحیه $${ x > a }$$ و نزدیک نقطه $${ x = a }$$ هستیم. همچنین حد چپ با علامت منفی (-) روی $${ x \to { a ^ - } }$$ نمایش داده می‌شود و در حد چپ در ناحیه $${ x < a }$$ و نزدیک نقطه $${ x = a }$$ قرار داریم.

بنابراین در مثال‌های مختلف توجه کنید که حد معمولی تابع در یک نقطه خواسته شده یا مثال مورد نظر به دنبال یافتن حد چپ یا راست در یک نقطه مشخص است. در مثال‌های زیر نحوه محاسبه حد یک طرفه به صورت دقیق مورد مطالعه قرار می‌گیرد.

مثال 1

حد یک طرفه (حد چپ و راست) تابع پله را در نقطه $${ t = 0 }$$ محاسبه کنید.

$${ \large \mathop { \lim } \limits _ { t \to { 0 ^ + } } H \left ( t \right ) \hspace { 0.25 in } \, \hspace { 0.25 in } \hspace { 0.25 in } \mathop { \lim } \limits _ { t \to { 0 ^ - } } H \left ( t \right ) }$$

تابع پله را به صورت زیر در نظر بگیرید.

$$ { \large \begin {align*} H \left ( t \right ) = \left \{ \begin {array} { ll } \displaystyle 0 & { \mbox { if } } t < 0 \\ 1 & { \mbox { if } } t \ge 0 \end {array} \right. \end {align*} } $$

این تابع را می‌توان به شکل گرافیکی زیر نمایش داد.

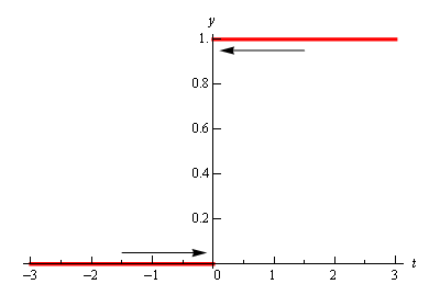
همانطور که مشاهده می‌شود، در صورتی که در سمت راست $${ t = 0 }$$ قرار داشته باشیم، تابع مقدار یک را نشان می‌دهد و در صورتی که از این سمت به مقدار $${ t = 0 }$$ نزدیک شویم، در واقع حد راست تابع پله در نقطه $${ t = 0 }$$ را محاسبه کردیم. بنابراین داریم:

$${ \large \mathop { \lim } \limits _ { { t } \to { 0 ^ { + } } } { H } \left ( { t } \right ) = 1 }$$

در حالت دیگر توجه کنید که اگر در سمت چپ نقطه $${ t = 0 }$$ قرار داشته باشیم، مقدار تابع برابر با صفر است. بنابراین در حد نشان داده شده، حد چپ، حالتی را نشان می‌دهد که از سمت چپ نقطه $${ t = 0 }$$ به این نقطه نزدیک شویم. این حد را می‌توان به شکل زیر نمایش داد.

$${ \large \mathop { \lim } \limits _ { t \to { 0 ^ { - } } } { H } \left ( { t } \right ) = 0 }$$

توجه کنید که در این مثال، بررسی حدهای یک طرفه تابع پله در نقطه $${ t = 0 }$$ انجام شد، در حالیکه حد خود این تابع در نقطه $${ t = 0 }$$ موجود نیست. دلیل موجود نبودن حد تابع در این نقطه این است که حد چپ و راست آن با یکدیگر برابر نیستند.

مثال 2

حدهای یک طرفه زیر را محاسبه کنید.

$${ \large \mathop { \lim } \limits _ { { t } \to { 0 ^ { + } } } \, \, \cos \left ( { \frac { \pi } { t } } \right ) \hspace { 0.5 in } \mathop { \lim } \limits _ { { t } \to { 0 ^ { - } } } \, \, \cos \left ( { \frac { \pi } { t } } \right) }$$

در ابتدا تابع نشان داده شده در بالا را بر حسب t به شکل زیر رسم می‌کنیم.

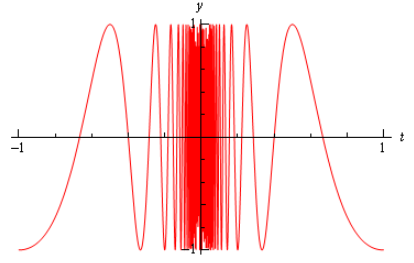
همانطور که مشاهده می‌شود، این تابع در نزدیکی نقطه $${ t = 0 }$$ در یک نقطه به خصوص قرار نمی‌گیرد. بنابراین حد این تابع در سمت چپ و راست به مقدار مشخصی میل نمی‌کند و در نتیجه می‌توان بیان کرد که حد چپ و راست این تابع در نزدیکی نقطه $${ t = 0 }$$ وجود ندارد.

بر این اساس، همانطور که ممکن است حد تابع در یک نقطه وجود نداشته باشد، احتمال این نیز وجود دارد که حدهای یک طرفه تابع در یک نقطه نیز موجود نباشند.

مثال 3

حدهای یک طرفه تابع $${ g ( x ) }$$ را در نقطه $${ x = 2 }$$ محاسبه کنید. این حدها در رابطه زیر نشان داده شده‌اند.

$${ \large \mathop { \lim } \limits _ { x \to { 2 ^ + } } g \left ( x \right ) \hspace { 0.25 in } { \rm { , } } \hspace { 0.25 in } \mathop { \lim } \limits _ { x \to { 2 ^ - } } g \left ( x \right ) }$$

همچنین توجه کنید که تابع $${ g ( x ) }$$ نیز به شکل زیر قابل نمایش است.

$$ { \large \begin {align*} g \left ( x \right ) = \left \{ \begin {array} { ll } \displaystyle \frac { { { x ^ 2 } + 4 x - 1 2 } } { { { x ^ 2 } - 2 x } } & { \mbox { if } } x \ne 2 \\ 6 & { \mbox { if } } x = 2 \end {array} \right . \end {align*} } $$

توجه کنید که برای محاسبه حد این تابع، کافی است که نمودار این تابع را رسم کنیم. این موضوع در شکل زیر به خوبی به تصویر کشیده شده است.

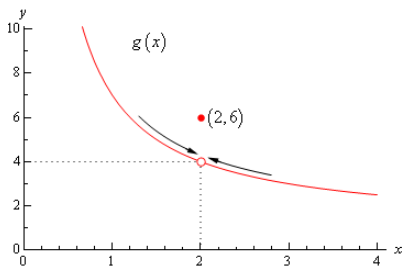
در این مثال، زمانی که از هر دو طرف نقطه $${ x = 2 }$$ به این نقطه نزدیک شویم، مقدار تابع به عدد 4 میل می‌کند. بنابراین می‌توان نتیجه گرفت که حد چپ و راست این تابع در نقطه $${ x = 2 }$$ برابر با 4 است. این موضوع را می‌توان با استفاده از رابطه‌های زیر به خوبی نمایش داد.

$${ \large \begin {align*} \mathop { \lim } \limits _ { x \to { 2 ^ + } } g \left ( x \right ) = 4 \hspace { 0.25 in } \hspace { 0.25 in } \hspace { 0.25 in } \mathop { \lim } \limits _ { x \to { 2 ^ - } } g \left ( x \right ) = 4 \end {align*} }$$

بنابراین همانطور که در مثال‌های بالا بیان شده است، در صورتی که حد چپ و حد راست یک تابع با یکدیگر برابر باشند، حد تابع در آن نقطه موجود است. بنابراین فرض کنید که رابطه زیر برای تابع $${ f ( x ) }$$ برقرار است.

$${ \large \begin {align*} \mathop { \lim } \limits _ { x \to { a ^ + } } f \left ( x \right ) = \mathop { \lim } \limits _ { x \to { a ^ - } } f \left ( x \right ) = L \end {align*} }$$

در این صورت، حد تابع $${ f ( x ) }$$ برابر است با:

$${ \large \begin {align*} \mathop { \lim } \limits _ { x \to a } f \left ( x \right ) = L \end {align*} }$$

توجه کنید که عکس رابطه بالا نیز برقرار است. در واقع یعنی اگر رابطه زیر را داشته باشیم:

$${ \large \begin {align*} \mathop { \lim } \limits _ { x \to a } f \left ( x \right ) = L \end {align*} }$$

آن‌گاه حد چپ و راست این تابع را می‌توان به شکل زیر بیان کرد.

$${ \large \begin {align*} \mathop { \lim } \limits _ { x \to { a ^ + } } f \left ( x \right ) = \mathop { \lim } \limits _ { x \to { a ^ - } } f \left ( x \right ) = L \end {align*} }$$

برای بررسی دقیق این موضوعات، مثال زیر را در نظر بگیرید.

مثال 4

نمودار زیر را در نظر بگیرید.

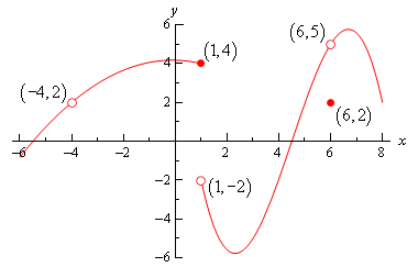
موارد خواسته شده زیر را در نقاط مختلف مورد محاسبه قرار دهید.

• $${ f ( - 4 ) }$$، $${ \mathop { \lim } \limits _ { x \to - { 4 ^ - } } f \left ( x \right ) }$$، $${ \mathop { \lim } \limits _ { { x } \to - { 4 ^ { + } } } f \left ( { x } \right ) }$$ و $${ \mathop { \lim } \limits _ { { x } \to - { 4 } } { f } \left ( x \right ) }$$ را بیابید.
• $${ f ( 1 ) }$$، $${ \mathop { \lim } \limits _ { x \to { 1 ^ - } } f \left ( x \right ) }$$، $${ \mathop { \lim } \limits _ { { x } \to { 1 ^ { + } } } f \left ( { x } \right ) }$$ و $${ \mathop { \lim } \limits _ { { x } \to { 1 } } { f } \left ( x \right ) }$$ را بیابید.
• $${ f ( 6 ) }$$، $${ \mathop { \lim } \limits _ { x \to { 6 ^ - } } f \left ( x \right ) }$$، $${ \mathop { \lim } \limits _ { { x } \to { 6 ^ { + } } } f \left ( { x } \right ) }$$ و $${ \mathop { \lim } \limits _ { { x } \to { 6 } } { f } \left ( x \right ) }$$ را بیابید.

پاسخ قسمت اول:

همانطور که در نمودار فوق مشاهده می‌شود، مقدار $${ f ( - 4 ) }$$ وجود ندارد و همچنین حد چپ این تابع در نزدیکی نقطه 4-، یعنی زمانی که از نقاط کمتر از 4- به این عدد نزدیک شویم، برابر با 2 است. این موضوع را می‌توان به شکل $${ \mathop { \lim } \limits _ { x \to - { 4 ^ - } } f \left ( x \right ) = 2 }$$ نمایش داد.

همچنین برای محاسبه حد راست این تابع در نقطه $${ x = - 4 }$$، از سمت راست به این نقطه نزدیک می‌شویم. در این حالت، حد این تابع برابر با $${ \mathop { \lim } \limits _ { x \to - { 4 ^ + } } f \left ( x \right ) = 2 }$$ خواهد بود.

بر این اساس حد این تابع، زمانی که مقدار $${ x }$$ به سمت $${ - 4 }$$ میل می‌کند، با محاسبه حد چپ و راست تابع در این نقطه امکان پذیر است. در واقع از آنجایی که حد چپ و راست تابع در نقطه $${ x = - 4 }$$، برابر با $$2$$ است، می‌توان نتیجه گرفت که حد تابع نیز برابر با $$2$$ است. این موضوع را می‌توان به شکل $${ \mathop { \lim } \limits _ { x \to - 4 } f \left ( x \right ) = 2 }$$ نمایش داد.

پاسخ قسمت دوم:

در این قسمت، همان روند توضیح داده شده در قسمت اول، برای حالتی انجام می‌شود که $${ x = 1 }$$ است.

همانطور که مشاهده می‌شود، مقدار این تابع در نقطه $${ x = 1 }$$ برابر با $$4$$ است. بنابراین می‌توان مقدار این تابع را با استفاده از رابطه زیر بیان کرد.

$${ \large f \left ( 1 \right ) = 4 }$$

همچنین همانطور که در شکل بالا مشاهده می‌شود، زمانی که از سمت چپ به نقطه $${ x = 1 }$$ نزدیک می‌شویم، تابع به سمت عدد 4 میل می‌کند. بنابراین می‌توان بیان کرد که حد چپ این تابع در نقطه $${ x = 1 }$$ برابر با 4 است. این موضوع با استفاده از رابطه زیر نشان داده شده است.

$${ \large \mathop { \lim } \limits _ { x \to { 1 ^ - } } f \left ( x \right ) = 4 }$$

با توجه به توضیحات بالا، حد راست این تابع در نقطه $${ x = 1 }$$ را نیز می‌توان به شکل زیر نمایش داد.

$${ \large \mathop { \lim } \limits _ { { x } \to { 1 ^ { + } } } { f } \left ( { x } \right ) = - 2 }$$

توجه کنید که حد یک طرفه یعنی حدهای راست و چپ این تابع در نقطه $${ x = 1 }$$ با یکدیگر برابر نیستند، بنابراین حد تابع در این نقطه وجود ندارد.

پاسخ قسمت سوم:

روندی که در دو قسمت قبلی توضیح داده شد را می‌توانید برای قسمت سوم نیز به کار ببرید. بنابراین این قسمت برای تمرین به عهده شما واگذار شده است و تنها به ارائه پاسخ نهایی آن اکتفا می‌کنیم.

$${ \large f \left ( 6 \right ) = 2 }$$

$${ \large \mathop { \lim } \limits _ { x \to { 6 ^ - } } f \left ( x \right ) = 5 }$$

$${ \large \mathop { \lim } \limits _ { x \to { 6 ^ + } } f \left ( x \right ) = 5 }$$

$${ \large \mathop { \lim } \limits _ { x \to 6 } f \left ( x \right ) = 5 }$$

بنابراین همانطور که در این مطلب بیان شد، برای محاسبه حد تابع در یک نقطه مشخص، نیاز به محاسبه حد یک طرفه آن تابع یعنی حد چپ و راست در همان نقطه مشخص داریم.

در صورتی که به مباحث مرتبط در زمینه ریاضیات پایه علاقه‌مند هستید، آموز‌ش‌های زیر به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش دانشگاهی
• مجموعه آموزش‌های ریاضیات
• دامنه و برد تابع — به زبان ساده
• حد در ریاضی — به زبان ساده
• حد در بینهایت — به زبان ساده
• حد بینهایت — به زبان ساده
• اتحاد و تجزیه در ریاضی — به زبان ساده

^^