در آموزشهای قبلی مجله فرادرس ، روشهای مختلف انتگرالگیری نامعین را معرفی کردیم. همچنین با روشهای عددی انتگرالگیری مانند قاعده سیمپپسون و قاعده ذوزنقهای آشنا شدیم. در این آموزش، «قضیه اساسی حسابان» را معرفی میکنیم که قضیهای بسیار مهم در حساب دیفرانسیل و انتگرال است. با استفاده از قضیه اساسی حسابان (Fundamental Theorem of Calculus) میتوان انتگرال معین و مشتق انتگرال را به آسانی محاسبه کرد.
فیلم آموزشی قضیه اساسی حسابان قضیه اساسی حسابان، دو بخش دارد: یکی برای محاسبه انتگرال معین و دیگری برای محاسبه مشتق انتگرال تابع. در ادامه، این دو بخش از این قضیه را معرفی کرده و اثبات آنها را بیان میکنیم.
بخش اول قضیه اساسی حسابان
بخش اول قضیه حسابان بیان میکند که اگر P ( x ) = ∫ a x f ( t ) d t \displaystyle { \large { { P } { \left ( { x } \right ) } = { \int _ { { a } } ^ { { x } } } { f { { \left ( { t } \right ) } } } { d } { t } } } P ( x ) = ∫ a x f ( t ) d t P ′ ( x ) = f ( x ) \displaystyle { \large { { P } ^ \prime { \left ( { x } \right ) } ={ f { { \left ( { x } \right ) } } } } } P ′ ( x ) = f ( x )
بخش اول قضیه اساسی حسابان به صورت d d x ∫ a x f ( t ) d t = f ( x ) \displaystyle { \large { \frac { { d } } { { { d } { x } } } { \int _ { { a } } ^ { { x } } } { f { { \left ( { t } \right ) } } } { d } { t } = { f { { \left ( { x } \right ) } } } } } d x d ∫ a x f ( t ) d t = f ( x ) f f f
اثبات
فرض کنید P ( x ) = ∫ a x f ( t ) d t \displaystyle { \large { { P } { \left ( { x } \right ) } = { \int _ { { a } } ^ { { x } } } { f { { \left ( { t } \right ) } } } { d } { t } } } P ( x ) = ∫ a x f ( t ) d t x x x x + h \displaystyle { \large { { x } + { h } } } x + h ( a , b ) \displaystyle { \large { { \left ( { a} , { b } \right ) } } } ( a , b )
P ( x + h ) − P ( x ) = ∫ a x + h f ( t ) d t − ∫ a x f ( t ) d t \large \displaystyle { \large { { P } { \left ( { x } + { h } \right ) } - { P } { \left ( { x } \right ) } = { \int _ { { a } } ^ { { { x } + { h } } } } { f { { \left ( { t } \right ) } } } { d } { t } - { \int _ { { a } } ^ { { x } } } { f { { \left ( { t } \right ) } } } { d } { t } } } P ( x + h ) − P ( x ) = ∫ a x + h f ( t ) d t − ∫ a x f ( t ) d t
اکنون از خاصیت مجاورت انتگرال استفاده میکنیم و یکی از آنها را به دو انتگرال میشکنیم:
حال از قضیه مقدار میانگین برای انتگرال استفاده میکنیم. این قضیه، تساوی زیر را بیان میکند:
∫ x x + h f ( t ) d t = n ( x + h − x ) = n h \large \displaystyle { \large { { \int _ { { x } } ^ { { { x } + { h } } } } { f { { \left ( { t } \right ) } } } { d } { t } = { n } { \left ( { x } + { h } - { x } \right ) } = { n } { h } } } ∫ x x + h f ( t ) d t = n ( x + h − x ) = n h
که در آن، m ′ ≤ n ≤ M ′ \displaystyle { \large { { m } ^ \prime \le { n } \le { M } ^ \prime } } m ′ ≤ n ≤ M ′ M ′ \displaystyle{\large{{M}'}} M ′ m ′ \displaystyle{\large{{m}'}} m ′ f f f [ x , x + h ] \displaystyle { \large { { \left [ { x } , { x } + { h } \right ] } } } [ x , x + h ]
بنابراین، تساوی P ( x + h ) − P ( x ) = n h \displaystyle { \large { { P } { \left ( { x } + { h } \right ) } - { P } { \left ( { x } \right ) } = { n } { h } } } P ( x + h ) − P ( x ) = n h h → 0 \displaystyle{\large{{h}\to{0}}} h → 0 P ( x + h ) − P ( x ) → 0 \displaystyle { \large { { P } { \left ( { x } + { h } \right ) } - { P } { \left ( { x } \right ) } \to { 0 } } } P ( x + h ) − P ( x ) → 0 P ( x + h ) → P ( x ) \displaystyle { \large { { P } { \left ( { x } + { h } \right ) } \to { P } { \left ( { x } \right ) } } } P ( x + h ) → P ( x ) P ( x ) P ( x ) P ( x )
بدون از دست دادن کلیت مسئله، فرض میکنیم h > 0 h > 0 h > 0 f f f [ x , x + h ] \displaystyle { \large { { \left [ { x } , { x } + { h } \right ] } } } [ x , x + h ] c c c d d d [ x , x + h ] \displaystyle { \large { { \left [ { x } , { x } + { h } \right ] } } } [ x , x + h ] f ( c ) = m \displaystyle { \large { { f { { \left ( { c } \right ) } } } = { m } } } f ( c ) = m f ( d ) = M \displaystyle { \large { { f { { \left ( { d } \right ) } } } ={ M } } } f ( d ) = M m m m M M M f f f [ x , x + h ] \displaystyle { \large { { \left [ { x } , { x } + { h } \right ] } } } [ x , x + h ]
بنابراین، نامساوی زیر را داریم:
m ( x + h − x ) ≤ ∫ x x + h f ( t ) d t ≤ M ( x + h − h ) \large \displaystyle { \large { { m } { \left ( { x } + { h } - { x } \right ) } \le { \int _ { { x } } ^ { { { x } + { h } } } } { f { { \left ( { t } \right ) } } } { d } { t } \le { M } { \left ( { x } + { h } - { h } \right ) } }} m ( x + h − x ) ≤ ∫ x x + h f ( t ) d t ≤ M ( x + h − h )
یا
m ≤ P ( x + h ) − P ( x ) h ≤ M \large \displaystyle { \large { { m } \le \frac { { { P } { \left ( { x } + { h } \right ) } - { P } { \left ( { x } \right ) } } } { { h } } \le { M } } } m ≤ h P ( x + h ) − P ( x ) ≤ M
عبارت اخیر را میتوانیم بر h > 0 h > 0 h > 0
m ≤ 1 h ∫ x x + h f ( t ) d t ≤ M \large \displaystyle { \large { { m } \le \frac { { 1 } } { { h } } { \int _ { { x } } ^ { {{ x } + { h } } } } { f { { \left ( { t } \right ) } } } { d } { t } \le { M } } } m ≤ h 1 ∫ x x + h f ( t ) d t ≤ M
یا
m ≤ P ( x + h ) − P ( x ) h ≤ M \large \displaystyle { \large { { m } \le \frac { { { P }{ \left ( { x } + { h } \right ) } - { P } { \left ( { x } \right ) } } } { { h } } \le { M } } } m ≤ h P ( x + h ) − P ( x ) ≤ M
در نهایت، میتوان نوشت:
f ( c ) ≤ P ( x + h ) − P ( x ) h ≤ f ( d ) \large \displaystyle { \large { { f { { \left ( { c } \right ) } } } \le \frac { { { P } { \left ( { x } + { h } \right ) } - { P } { \left ( { x } \right ) } } } { { h } } \le { f { { \left ( { d } \right ) } } } } } f ( c ) ≤ h P ( x + h ) − P ( x ) ≤ f ( d )
به طریق مشابه، نامساوی بالا را برای h < 0 \displaystyle { \large { { h } < { 0 } } } h < 0
اکنون فرض کنید h → 0 \displaystyle { \large { { h } \to { 0 } } } h → 0 c c c d d d x x x x + h x+ h x + h c → x \displaystyle { \large { { c } \to { x } } } c → x d → x \displaystyle { \large { { d } \to { x } } } d → x
بنابراین، از آنجایی که f f f
lim h → 0 f ( c ) = lim c → x f ( c ) = f ( x ) \large \displaystyle { \large { \lim _ { {{ h } \to { 0 } } } { f { { \left ( { c } \right ) } } } = \lim _ { { { c } \to { x } } } { f { { \left ( { c } \right ) } } } = { f { { \left ( { x } \right ) } } } } } h → 0 lim f ( c ) = c → x lim f ( c ) = f ( x )
و
lim h → 0 f ( d ) = lim d → x f ( d ) = f ( x ) \large \displaystyle { \large { \lim _ { { { h } \to { 0 } } } { f { { \left ( { d } \right ) } } } = \lim _ { { { d } \to { x } } } { f { { \left ( { d } \right ) } } } = { f { { \left ( { x } \right ) } } } } } h → 0 lim f ( d ) = d → x lim f ( d ) = f ( x )
با توجه به نامساوی آخر و قضیه فشردگی ، میتوانیم تساوی زیر را نتیجه بگیریم:
lim h → 0 P ( x + h ) − P ( x ) h = f ( x ) \large \displaystyle { \large { \lim _ { { { h } \to { 0 } } } \frac { { { P } { \left ( { x } + { h } \right ) } - { P } { \left ( { x } \right ) } } } { { h } } = { f { { \left ( { x } \right ) } } } } } h → 0 lim h P ( x + h ) − P ( x ) = f ( x )
سمت چپ معادله بالا، تعریف مشتق P ( x ) P(x) P ( x )
P ′ ( x ) = f ( x ) \large \displaystyle { \large { { P } ^ \prime { \left ( { x } \right ) } = { f { { \left ( { x } \right ) } } } } } P ′ ( x ) = f ( x )
و بدین ترتیب، بخش اول قضیه اثبات میشود.
بخش دوم قضیه اساسی حسابان
بخش دوم قضیه اساسی حسابان بیان میکند که تساوی ∫ a b f ( x ) d x = F ( b ) − F ( a ) \displaystyle { \large { { \int _ { { a } } ^ { { b } } } { f { { \left ( { x } \right ) } } } { d } { x } = { F } { \left ( { b } \right ) } - { F } { \left ( { a } \right ) } } } ∫ a b f ( x ) d x = F ( b ) − F ( a ) F F F f f f F ′ = f \displaystyle { \large { { F } ^ \prime = { f { } } } } F ′ = f
بخش دوم قضیه اساسی حسابان، به صورت ∫ a b F ′ ( x ) d x = F ( b ) − F ( a ) \displaystyle { \large { { \int _ { { a } } ^ { { b } } } { F } ^ \prime { \left ( { x } \right ) } { d } { x} = { F } { \left ( { b } \right ) } - { F } { \left ( { a } \right ) } } } ∫ a b F ′ ( x ) d x = F ( b ) − F ( a ) f f f F F F F ( b ) − F ( a ) \displaystyle { \large { { F } { \left ( { b } \right ) } - { F }{ \left ( { a } \right ) } } } F ( b ) − F ( a )
اثبات
بازه [ a , b ] \displaystyle { \large { { \left [ { a } , { b } \right ] } } } [ a , b ] n n n x 0 ( = a ) , x 1 , x 2 , … , x n ( = b ) \displaystyle { \large { { x } _ { { 0 } } { \left ( = { a } \right ) }, { x } _ { { 1 } } , { x } _ { { 2 } } , \ldots , { x } _ { { n } } { \left ( = { b } \right ) } } } x 0 ( = a ) , x 1 , x 2 , … , x n ( = b ) Δ x = b − a n \displaystyle { \large { \Delta { x } = \frac { {{ b } - { a } } } { { n } } } } Δ x = n b − a F F F f f f
با جمع و تفریق جبری جملات مشابه، میتوانیم تفریق کلی مقادیر F F F
F ( b ) − F ( a ) = F ( x n ) − F ( x 0 ) \large \displaystyle { \large { { F } { \left ( { b } \right ) } - { F } { \left ( { a } \right ) } = { F } { \left ( { x } _ { { n } } \right ) } - { F } { \left ( { x } _ { { 0 } } \right ) } } } F ( b ) − F ( a ) = F ( x n ) − F ( x 0 )
= F ( x n ) − F ( x n − 1 ) + F ( x n − 2 ) + … + F ( x 2 ) − F ( x 1 ) + F ( x 1 ) − F ( x 0 ) \large \displaystyle { \large { = { F } { \left ( { x } _ { { n } } \right ) } - { F } { \left ( { x } _ { { { n } - { 1 } } } \right ) } + { F } { \left ( { x } _ { { { n } - { 2 } } } \right ) } + \ldots + { F } { \left ( { x } _ { { 2 } } \right ) } - { F }{ \left ( { x } _{ { 1 } } \right ) } + { F } { \left ( { x } _ { { 1 } } \right ) } - { F } { \left ( { x } _ { { 0 } } \right ) } } } = F ( x n ) − F ( x n − 1 ) + F ( x n − 2 ) + … + F ( x 2 ) − F ( x 1 ) + F ( x 1 ) − F ( x 0 )
= ∑ i = 1 n ( F ( x i ) − F ( x i − 1 ) ) \large \displaystyle { \large { = { \sum _ { { { i } = { 1 } } } ^ { { n } } } { \left ( { F } { \left ( { x } _ { { i } } \right ) } - { F } { \left ( { x } _ { { { i } - { 1 } } } \right ) } \right ) } } } = i = 1 ∑ n ( F ( x i ) − F ( x i − 1 ) )
از آنجایی که F F F [ x i − 1 , x i ] \displaystyle { \large { { \left [ { x } _ { { { i } - { 1 } } } , { x } _ { { i } } \right ] } } } [ x i − 1 , x i ]
بنابراین، عدد x i ⋆ \displaystyle{\large{{{x}_{{i}}^{{\star}}}}} x i ⋆ x i − 1 \displaystyle{\large{{x}_{{{i}-{1}}}}} x i − 1 x i \displaystyle{\large{{x}_{{i}}}} x i
F ( x i ) − F ( x i − 1 ) = F ′ ( x i ⋆ ) ( x i − x i − 1 ) = f ( x i ⋆ ) Δ x \large \displaystyle { \large { { F } { \left ( { x } _{ { i } } \right ) } - { F } { \left ( { x } _ { { { i } - { 1 } } } \right ) } = { F } ^ \prime { \left ( { { x } _ { { i } } ^ { { \star } } } \right ) } { \left ( { x } _ { { i } } - { x } _ { {{ i } - { 1 } } } \right ) } = { f { { \left ({ { x } _ { { i }} ^ { { \star } } } \right ) }} } \Delta { x }} } F ( x i ) − F ( x i − 1 ) = F ′ ( x i ⋆ ) ( x i − x i − 1 ) = f ( x i ⋆ ) Δ x
در نتیجه، داریم:
F ( b ) − F ( a ) = ∑ i = 1 n f ( x i ⋆ ) Δ x \large \displaystyle { \large { { F } { \left ( { b } \right ) } - { F } { \left ( { a} \right ) } = { \sum _ {{ { i } = { 1 } } } ^ { { n } } } { f { { \left ( { { x }_ { { i } } ^ { { \star } } } \right ) } } } \Delta { x } } } F ( b ) − F ( a ) = i = 1 ∑ n f ( x i ⋆ ) Δ x
اکنون حد بینهایت دو سمت تساوی اخیر را حساب میکنیم. سمت چپ مقدار ثابتی است و سمت راست، مجموع ریمان برای تابع f f f
F ( b ) − F ( a ) = lim n → ∞ ∑ i = 1 n f ( x i ⋆ ) Δ x = ∫ a b f ( x ) d x \large \displaystyle { \large { { F } { \left ( { b } \right ) } - { F } { \left ( { a } \right ) } = \lim _ { { { n } \to \infty } }{ \sum _ { { { i } = { 1} } } ^ { { n }} } { f { { \left ( { { x } _ { { i }} ^ { { \star}}} \right)}} } \Delta{x}={\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}}} F ( b ) − F ( a ) = n → ∞ lim i = 1 ∑ n f ( x i ⋆ ) Δ x = ∫ a b f ( x ) d x
و بدین ترتیب، بخش دوم قضیه اساسی حسابان اثبات میشود.
مثالها
در ادامه، چند مثال را درباره قضیه اساسی حسابان بیان میکنیم.
مثال ۱
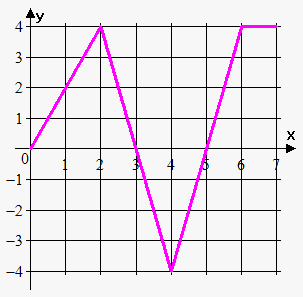
نمودار تابع f f f
اگر P ( x ) = ∫ 0 x f ( t ) d t \displaystyle { \large { { P } { \left ( { x } \right ) } = { \int _ { { 0 } } ^ { { x } } } { f { { \left ( { t } \right ) } } } { d } { t } } } P ( x ) = ∫ 0 x f ( t ) d t P ( 0 ) P(0) P ( 0 ) P ( 1 ) P(1) P ( 1 ) P ( 2 ) P(2) P ( 2 ) P ( 3 ) P(3) P ( 3 ) P ( 4 ) P(4) P ( 4 ) P ( 5 ) P(5) P ( 5 ) P ( 6 ) P(6) P ( 6 ) P ( 7 ) P(7) P ( 7 ) P P P
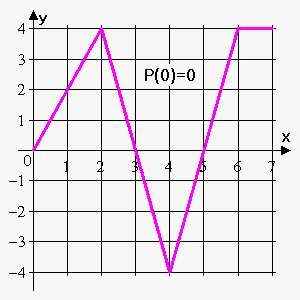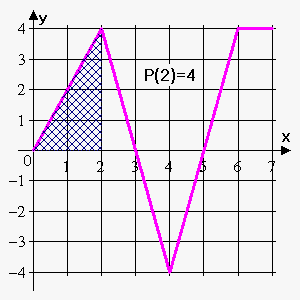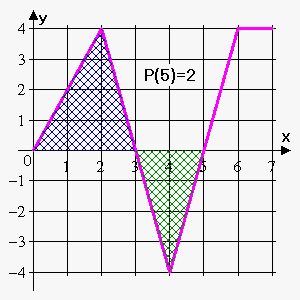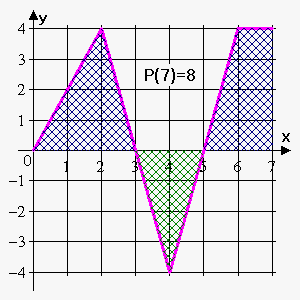
حل: ابتدا به سادگی میتوانیم بنویسیم:
P ( 0 ) = ∫ 0 0 f ( t ) d t = 0 \large \displaystyle { \large { { P } { \left ( { 0 } \right ) } ={ \int _ { { 0 } } ^ { { 0 } } } { f { { \left ( { t } \right ) } } } { d } { t } = { 0 } } } P ( 0 ) = ∫ 0 0 f ( t ) d t = 0
مقدار P ( 1 ) P(1) P ( 1 ) 1 1 1 2 2 2
P ( 1 ) = ∫ 0 1 f ( t ) d t = 1 2 ⋅ 1 ⋅ 2 = 1 \large \displaystyle { \large { { P } { \left ( { 1 } \right ) } = { \int _ { { 0 } } ^ { { 1 } } } { f { { \left ( { t } \right ) } } } { d } { t } } } = \frac { { 1 } } { { 2 } } \cdot { 1 } \cdot { 2 } = { 1 } P ( 1 ) = ∫ 0 1 f ( t ) d t = 2 1 ⋅ 1 ⋅ 2 = 1
مقدار P ( 2 ) P(2) P ( 2 ) 2 2 2 4 4 4
P ( 2 ) = ∫ 0 2 f ( t ) d t = 1 2 ⋅ 2 ⋅ 4 = 4 \large \displaystyle { \large { { P } { \left ( { 2 } \right ) } = { \int _ { { 0 } } ^ { { 2 } } } { f { { \left ( { t } \right ) } } } { d } { t } } } = \frac { { 1 } } { { 2 } } \cdot { 2 } \cdot { 4 } = { 4 } P ( 2 ) = ∫ 0 2 f ( t ) d t = 2 1 ⋅ 2 ⋅ 4 = 4
مساحت از 0 0 0 3 3 3 0 0 0 2 2 2 2 2 2 3 3 3 1 1 1 4 4 4
P ( 3 ) = ∫ 0 3 f ( t ) d t = ∫ 0 2 f ( t ) d t + ∫ 2 3 f ( t ) d t = 4 + 1 2 ⋅ 1 ⋅ 4 = 6 \large \displaystyle { \large { { P } { \left ( { 3 } \right ) } ={ \int _ { { 0 } } ^ { { 3 } } } { f { { \left ( { t } \right ) } } } { d } { t } = { \int _ { { 0 } } ^ { { 2 } } } { f { { \left ( { t } \right ) } } } { d } { t } + { \int _ { { 2 } } ^ { { 3 } } } { f { { \left ( { t } \right ) } } } { d } { t } = { 4 } + \frac { { 1 } } { { 2 } } \cdot { 1 } \cdot { 4 } = { 6 } } } P ( 3 ) = ∫ 0 3 f ( t ) d t = ∫ 0 2 f ( t ) d t + ∫ 2 3 f ( t ) d t = 4 + 2 1 ⋅ 1 ⋅ 4 = 6
به طریق مشابه، برای P ( 4 ) P(4) P ( 4 )
P ( 4 ) = P ( 3 ) + ∫ 3 4 f ( t ) d t = 6 − 1 2 ⋅ 1 ⋅ 4 = 4 \large \displaystyle { \large { { P } { \left ( { 4 } \right ) } = { P } { \left ( { 3 } \right ) } + { \int _ { { 3 } } ^ { { 4 } } } { f { { \left ( { t } \right ) } } } { d } { t } } } = { 6 } - \frac { { 1 } } { { 2 } } \cdot { 1 } \cdot { 4 } = { 4 } P ( 4 ) = P ( 3 ) + ∫ 3 4 f ( t ) d t = 6 − 2 1 ⋅ 1 ⋅ 4 = 4
و به همین ترتیب، P ( 5 ) P(5) P ( 5 ) P ( 6 ) P(6) P ( 6 ) P ( 7 ) P(7) P ( 7 )
P ( 5 ) = P ( 4 ) + ∫ 4 5 f ( t ) d t = 4 − 1 2 ⋅ 1 ⋅ 4 = 2 \large \displaystyle { \large { { P } { \left ( { 5 } \right ) } = { P } { \left ( { 4} \right ) } + { \int _ { { 4 } } ^ { { 5 } } } { f { { \left ( { t } \right ) } } } { d } { t } = { 4 } - \frac { { 1 } } { { 2 } } \cdot { 1 } \cdot { 4 } = { 2 } } } P ( 5 ) = P ( 4 ) + ∫ 4 5 f ( t ) d t = 4 − 2 1 ⋅ 1 ⋅ 4 = 2
P ( 6 ) = P ( 5 ) + ∫ 5 6 f ( t ) d t = 2 + 1 2 ⋅ 1 ⋅ 4 = 4 \large \displaystyle { \large { { P } { \left ( { 6 } \right ) } = { P } { \left ( { 5 } \right ) } + { \int _ { { 5 } } ^ { { 6 } } } { f { { \left ( { t } \right ) } } } { d } { t } = { 2 } + \frac { { 1 } } { { 2 } } \cdot { 1 } \cdot { 4 } = { 4 } } } P ( 6 ) = P ( 5 ) + ∫ 5 6 f ( t ) d t = 2 + 2 1 ⋅ 1 ⋅ 4 = 4
P ( 7 ) = P ( 6 ) + ∫ 6 7 f ( t ) d t = 4 + 1 ⋅ 4 = 8 \large \displaystyle { \large { { P } { \left ( { 7 } \right ) } = { P } { \left ( { 6 } \right ) } + { \int _ { { 6} } ^ { { 7 } } } { f { { \left ( { t } \right )} } } { d } { t } } } = { 4 } + { 1 } \cdot { 4 } = { 8 } P ( 7 ) = P ( 6 ) + ∫ 6 7 f ( t ) d t = 4 + 1 ⋅ 4 = 8
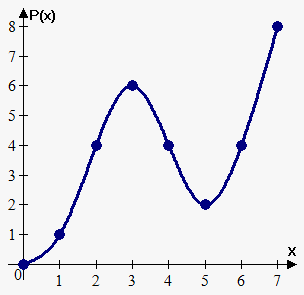
تصویر زیر، این مقادیر را به خوبی نشان میدهد.
نمودار P ( x ) P(x) P ( x )
مثال ۲
اگر P ( x ) = ∫ 1 x t 3 d t \displaystyle { \large { { P } { \left ( { x } \right ) } = { \int _ { { 1 } } ^ { { x } } } { { t } } ^ { { 3 } } { d } { t } } } P ( x ) = ∫ 1 x t 3 d t P ( x ) P(x) P ( x ) P ′ ( x ) P ^ \prime (x) P ′ ( x )
حل: با استفاده از بخش دوم قضیه اساسی حسابان، داریم:
P ( x ) = ∫ 1 x t 3 d t = ( t 4 4 ) ∣ 1 x = x 4 4 − 1 4 \large \displaystyle { \large { { P } { \left ( { x } \right ) } = { \int _{ { 1 } } ^ { { x} } } { { t } } ^ { { 3 } } { d } {t } ={ \left ( \frac { { { t } } ^ {{ 4 } } } {{ 4 } } \right ) } { { \mid } _ { { 1 } } ^ { { x } } } = \frac { { { x } } ^ { { 4 } } } { { 4 } } - \frac { { 1 } } { { 4 } } } } P ( x ) = ∫ 1 x t 3 d t = ( 4 t 4 ) ∣ 1 x = 4 x 4 − 4 1
در نتیجه، حاصل P ′ ( x ) P^ \prime (x ) P ′ ( x )
P ′ ( x ) = ( x 4 4 − 1 4 ) ′ = x 3 \large \displaystyle { \large { {P} ^ \prime { \left ( { x } \right ) } = { \left ( \frac { { { x } } ^ { { 4 } } } { { 4 } } - \frac { { 1 } } { { 4 } } \right ) } ^ \prime = { { x } } ^ { { 3} } } } P ′ ( x ) = ( 4 x 4 − 4 1 ) ′ = x 3
همانطور که میبینیم، P ′ ( x ) = f ( x ) P^ \prime (x) = f (x) P ′ ( x ) = f ( x )
مثال ۳
مشتق P ( x ) = ∫ 0 x t 3 + 1 d t \displaystyle { \large { { P } { \left ( { x } \right ) } = {\int _ { { 0 } } ^ { { x } } } \sqrt { { {{ t } } ^ { { 3 } } + { 1 } } } { d } { t } } } P ( x ) = ∫ 0 x t 3 + 1 d t
حل: با استفاده از بخش اول قضیه اساسی حسابان، داریم:
P ′ ( x ) = x 3 + 1 \displaystyle{\large{{P{^ \prime } } { \left ( { x } \right ) } = \sqrt { { { { x } } ^ { { 3} } + { 1 } } } } } P ′ ( x ) = x 3 + 1
مثال ۴
حاصل d d x ∫ 2 x 3 ln ( t 2 + 1 ) d t \displaystyle { \large { \frac { {d } } {{ { d }{ x } }} { \int _ { { 2 } } ^ { { { { x } } ^ { { 3 } } } } } { \ln { { \left ( { {t } } ^ { { 2} } + { 1 } \right ) } } } { d } { t } }} d x d ∫ 2 x 3 ln ( t 2 + 1 ) d t
حل: در این مثال، تابع ترکیبی P ( x 3 ) P (x^3) P ( x 3 ) قاعده زنجیرهای و قضیه اساسی حسابان استفاده میکنیم.
بنابراین، با در نظر گرفتن u = x 3 \displaystyle { \large { { u } = { { x} } ^ { {3 } } } } u = x 3 d u d x = ( x 3 ) ′ = 3 x 2 \displaystyle { \large { \frac { { { d } { u } } } { { { d } { x } } } = { \left ( { { x } } ^ { { 3 } } \right ) } ^ \prime = { 3 } { { x } } ^ { { 2 } } }} d x d u = ( x 3 ) ′ = 3 x 2
d d x ∫ 2 x 3 ln ( t 2 + 1 ) d t = d d u ∫ 2 u ln ( t 2 + 1 ) ⋅ d u d x \large \displaystyle \large { \frac { { d } } { { { d } { x } } } { \int _ { { 2 } } ^ { { { { x } } ^ { { 3 } } } } } { \ln { { \left ( { { t } } ^ { { 2 } } + { 1 } \right ) } } } { d } { t } = \frac { { d } } { { { d } { u } } } { \int _ { { 2 } } ^ { { u } } } { \ln { { \left ( { { t } } ^ { { 2 } } +{ 1 } \right ) } } } \cdot \frac { { { d } { u } } } { { { d } { x }}}} d x d ∫ 2 x 3 ln ( t 2 + 1 ) d t = d u d ∫ 2 u ln ( t 2 + 1 ) ⋅ d x d u
= d d u ∫ 2 u ln ( t 2 + 1 ) ⋅ 3 x 2 = ln ( u 2 + 1 ) ⋅ 3 x 2 \large = \frac { { d } } { { { d } { u } } } { \int _ { { 2 } } ^ { { u } } } { \ln { { \left ( { { t } } ^ { { 2 } } + { 1 } \right ) } }} \cdot { 3 } { { x } } ^ { { 2 } } \displaystyle { \large { = { \ln{ { \left ( { { u } } ^ { { 2 } } + { 1 } \right ) } } } \cdot { 3 } { { x } } ^ { { 2 } } }} = d u d ∫ 2 u ln ( t 2 + 1 ) ⋅ 3 x 2 = ln ( u 2 + 1 ) ⋅ 3 x 2
= ln ( ( x 3 ) 2 + 1 ) ⋅ 3 x 2 = 3 x 2 ln ( x 6 + 1 ) \large = { \ln { { \left ( { { \left ( { { x } } ^ { { 3 } } \right ) } } ^{ { 2 } } + { 1 } \right ) } } } \cdot { 3 } { { x } } ^ { { 2 } } = { 3 } { { x } } ^ { { 2 } } { \ln { { \left ( { { x } } ^ { { 6 } } + { 1 } \right ) } } } = ln ( ( x 3 ) 2 + 1 ) ⋅ 3 x 2 = 3 x 2 ln ( x 6 + 1 )
مثال ۵
انتگرال ∫ 0 5 e x d x \displaystyle { \large { { \int _ { { 0 } } ^ { { 5 } } } {{ e } } ^ { { x } } { d } {x } } } ∫ 0 5 e x d x
حل: با استفاده از بخش دوم قضیه اساسی حسابان، حاصل انتگرال به صورت زیر است:
∫ 0 5 e x d x = e x ∣ 0 5 = e 5 − e 0 = e 5 − 1 \large \displaystyle { \large { { \int _ { { 0 } } ^ { { 5 } } } { { e } } ^ { { x } } { d } { x } = { { e } } ^ { { x } } { { \mid } _ { {0 } } ^ { { 5 } } } = { { e } } ^ { { 5 } } - { { e } } ^ { { 0 } } = { { e } } ^ { { 5 } } - { 1 } } } ∫ 0 5 e x d x = e x ∣ 0 5 = e 5 − e 0 = e 5 − 1
مثال ۶
انتگرال ∫ 0 π 2 cos ( x ) d x \displaystyle { \large { { \int _ { { 0 } } ^ { { \frac { \pi }{ { 2 } } } } } { \cos { { \left ( { x } \right ) } } } { d } { x } } } ∫ 0 2 π cos ( x ) d x
حل: با استفاده از بخش دوم قضیه اساسی حسابان، داریم:
∫ 0 π 2 cos ( x ) d x = sin ( x ) ∣ 0 π 2 = sin ( π 2 ) − sin ( 0 ) = 1 \large \displaystyle { \large { { \int _ { { 0 } } ^ { { \frac { \pi } { { 2 } } } } } { \cos { { \left ( { x } \right ) } } } { d } { x } = { \sin { { \left ( { x } \right )} } } { { \mid } _ { { 0 } } ^ { { \frac { \pi } { { 2 } } } } } = { \sin { { \left ( \frac { \pi } { { 2 } } \right ) } } } - { \sin { { \left ( { 0 } \right ) } } } = { 1 } } } ∫ 0 2 π cos ( x ) d x = sin ( x ) ∣ 0 2 π = sin ( 2 π ) − sin ( 0 ) = 1
مثال ۷
انتگرال ∫ 0 2 ( 3 x 2 − 7 ) d x \displaystyle { \large { { \int _ { { 0 } } ^ { { 2 } } } { \left ( { 3 } { { x } } ^ { { 2 } } - { 7 } \right ) } { d } { x } } } ∫ 0 2 ( 3 x 2 − 7 ) d x
حل: با استفاده از بخش دوم قضیه اساسی حسابان، حاصل انتگرال برابر است با:
∫ 0 2 ( 3 x 2 − 7 ) d x = ∫ 0 2 3 x 2 d x − ∫ 0 2 7 d x \large \displaystyle { \large { { \int _ { { 0 } } ^ { { 2 } } } { \left ( { 3 } { { x } } ^ { { 2 } } - { 7 } \right ) } { d } { x } = { \int _ { { 0 } } ^ { { 2 } }} { 3 } { { x } } ^ { { 2 } } { d } { x } - { \int _ { { 0 } } ^ { { 2 } } } { 7 } { d } { x } }} ∫ 0 2 ( 3 x 2 − 7 ) d x = ∫ 0 2 3 x 2 d x − ∫ 0 2 7 d x
= 3 ∫ 0 2 x 2 d x − 7 ∫ 0 2 7 d x = 3 ( x 3 3 ) ∣ 0 2 − 7 ⋅ ( 2 − 0 ) \large = { 3 } { \int _ { { 0 } } ^ { { 2 } } } { { x } } ^ { { 2 } } { d } { x } - { 7 } { \int _ { { 0 } } ^ { { 2 } } } { 7 } { d } { x } \displaystyle { \large { = { 3 } { \left ( \frac { { { x } } ^ { { 3 } } } { { 3 } } \right ) } { { \mid } _ { { 0 } } ^ { { 2 } } } - { 7 } \cdot { \left ( { 2 } - { 0 } \right ) }}} = 3 ∫ 0 2 x 2 d x − 7 ∫ 0 2 7 d x = 3 ( 3 x 3 ) ∣ 0 2 − 7 ⋅ ( 2 − 0 )
= 3 ( 8 3 − 0 3 ) − 14 = − 6 \large = { 3 } { \left ( \frac { { 8 } } { { 3 } } - \frac { { 0 } } { { 3 } } \right ) } - { 1 4 } = - { 6 } = 3 ( 3 8 − 3 0 ) − 14 = − 6
مثال ۸
انتگرال ∫ 1 3 ( 2 t 5 − 8 t t + 7 t 2 + 1 ) d t \displaystyle { \large { { \int _ { { 1 } } ^ { { 3 } } } { \left ( \frac { { { 2 } { { t }} ^{ { 5 }} - { 8 } \sqrt { { { t } } } } }{{ t } } + \frac { { 7 } } { { { { t } } ^ { { 2 } } + { 1 } } } \right ) } { d } { t } } } ∫ 1 3 ( t 2 t 5 − 8 t + t 2 + 1 7 ) d t
حل: ابتدا انتگرال را به صورت زیر مینویسیم:
∫ 1 3 ( 2 t 5 − 8 t t + 7 t 2 + 1 ) d t = ∫ 1 3 ( 2 t 4 − 8 t − 1 2 + 7 t 2 + 1 ) d t \large \displaystyle { \large { { \int _ { { 1 } } ^ { { 3 } } } { \left ( \frac { { { 2 } { { t } } ^ { { 5 } } - { 8 } \sqrt { { { t } } } } } { { t } } + \frac { { 7 } } { { { { t } } ^ { { 2 } } + { 1 } } } \right ) } { d } { t } = { \int _ { { 1} } ^ { { 3 } } } { \left ( { 2 } { { t } } ^ { { 4 } } - { 8 } { { t } } ^ { { - \frac { { 1 } } { { 2 } } } } + \frac { { 7 } } { { { { t } } ^ { { 2 } } + { 1 } } } \right ) } { d } { t } } } ∫ 1 3 ( t 2 t 5 − 8 t + t 2 + 1 7 ) d t = ∫ 1 3 ( 2 t 4 − 8 t − 2 1 + t 2 + 1 7 ) d t
بنابراین، داریم:
∫ 1 3 ( 2 t 4 − 8 t − 1 2 + 7 t 2 + 1 ) d t = ( 2 5 t 5 − 16 t + 7 tan − 1 ( t ) ) ∣ 1 3 = ( 2 5 ( 3 ) 5 − 16 3 + 7 tan − 1 ( 3 ) ) − ( 2 5 ( 1 ) 5 − 16 1 + 7 tan − 1 ( 1 ) ) = 564 5 − 16 3 − 7 π 4 + 7 tan − 1 ( 3 ) ≈ 88.3327 \large \displaystyle { \large { { \int _ { { 1 } } ^ { { 3 } } } { \left ( { 2 } { { t } } ^ { { 4 } } - { 8 } { { t } } ^ { { - \frac { { 1 } } { { 2 } } } } + \frac { { 7 } } { { { { t } } ^ { { 2 } } + { 1 } } } \right ) } { d } { t } = { \left ( \frac { { 2 } } { { 5 } } { { t } } ^ { { 5 } } - { 1 6 } \sqrt {{ { t } }} + { 7 } { { \tan } } ^ { { - { 1 } } } { \left ( { t } \right ) } \right ) } { { \mid } _ { { 1 } } ^ { { 3 } } } } } \\ \large
\displaystyle { \large { = { \left ( \frac { { 2 } } { { 5 } } { { \left ( { 3 } \right ) } } ^ { { 5 } } - { 1 6 } \sqrt { { { 3 } } } + { 7 } { { \tan } } ^ { { - { 1 } } } { \left ( { 3 } \right ) } \right ) } - { \left ( \frac { { 2 } } { { 5 } } { { \left ( { 1 } \right ) } } ^ { { 5 } } - { 1 6 } \sqrt { { { 1 } } } + { 7 } { { \tan } } ^ { { - { 1 } } } { \left ( { 1 } \right ) } \right ) } } } \\ \large
\displaystyle { \large { = \frac { { 5 6 4 } } { { 5 } } - {1 6 } \sqrt { { { 3 } } } - \frac { { { 7 } \pi } } { { 4 } } + { 7 } { { \tan } } ^ { { - { 1 } } } { \left ( { 3 } \right ) } \approx { 8 8. 3 3 2 7 } } } ∫ 1 3 ( 2 t 4 − 8 t − 2 1 + t 2 + 1 7 ) d t = ( 5 2 t 5 − 16 t + 7 tan − 1 ( t ) ) ∣ 1 3 = ( 5 2 ( 3 ) 5 − 16 3 + 7 tan − 1 ( 3 ) ) − ( 5 2 ( 1 ) 5 − 16 1 + 7 tan − 1 ( 1 ) ) = 5 564 − 16 3 − 4 7 π + 7 tan − 1 ( 3 ) ≈ 88.3327
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
^^

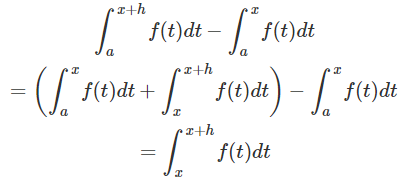













آموزک ویدئویی عالی بود