مشتق و محاسبات آن — به زبان ساده

مشتق (Derivative) از پرکاربردترین مفاهیم ابداع شده در ریاضیات است. در حقیقت میتوان گفت قلب ریاضیات مدرن، مفهوم مشتق است. در حالت کلی مشتق بر دو نوع مشتق ساده و جزئی است. البته مشتقات ساده را میتوان با دو روش صریح و ضمنی بدست آورد. در این مطلب از مجله فرادرس تنها روش صریح توضیح داده شده است. البته در آینده مشتق توابع لگاریتمی، توابع معکوس مثلثاتی و مشتق زنجیرهای را نیز توضیح خواهیم داد.
کاربرد مشتق در چیست؟
مفهوم مشتق در ریاضیات بیان میکند که یک پارامتر با چه سرعتی در زمان تغییر میکند. از این رو این ابزار در فیزیک کاربرد بسیاری دارد.
برای مثال تصور کنید که خودرویی در حال پیمودن مسافت مشخصی است. در این حالت اگر تغییرات مسافت پیموده شده نسبت به زمان معلوم باشد، میتوان نرخ این مسافت را در واحد زمان محاسبه کرد. از این رو در اکثر مسائلی که با سرعتِ تغییرِ یک پارامتر سروکار داریم، مشتق ظاهر خواهد شد.
مفهوم مشتق
همانطور که در بالا نیز اشاره شد، مشتق بیان میکند که یک تابع (مثلا جابجایی صورت گرفته توسط یک خودرو) با چه نرخی نسبت به متغیر وابستهاش تغییر میکند. برای نمونه در مثال خودرو، شیب تغییرات مسافت نسبت به زمان، همان مشتق است.
فرض کنید خودرویی فاصله مشخصی را میپیماید. همچنین تصور کنید که نمودار مسافت پیموده شده نسبت به زمان را در اختیار داریم. شکل زیر این تغییرات را نشان میدهد.
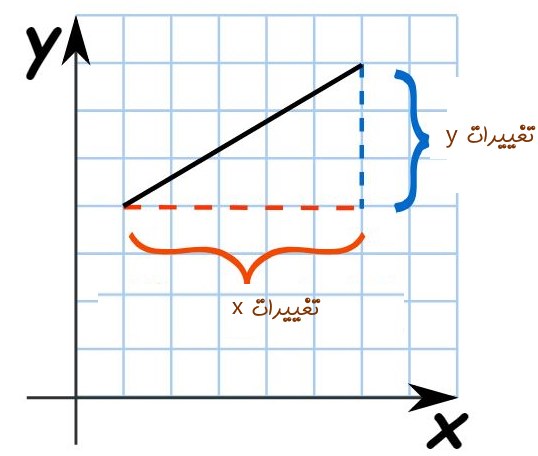
این نمودار بیان میکند که خودرو در هر لحظه در چه مکانی قرار گرفته. بنابراین با بدست آوردن شیب این نمودار، میتوان فهمید که در هر ثانیه این خودرو به چه میزان جابجا میشود. این عدد بدست آمده، همان مفهوم سرعت است.
حال تصور کنید که این تغییرات، همچون نمودار پایین غیرخطی باشند. به راستی در این حالت سرعت را چطور میتوان بدست آورد؟
فرض کنید میخواهیم شیب نمودار را در نقطه (x0,y0) بیابیم. از این رو به نقطه دومی هم نیاز داریم. اگر این نقطه را به فاصله زیادی از (x0,y0) در نظر بگیریم، شیب بین این دو نقطه، عدد دقیقی را از شیب در نقطه (x0,y0) بدست نمیدهد. بنابراین بایستی چه کرد؟ حال نقطه دوم را بسیار نزدیک به (x0,y0) در نظر میگیریم. در حقیقت مختصات نقطه دوم به صورت $$(x_0+\Delta x,y_0+\Delta y)$$ در نظر گرفته شده. بنابراین شیب بین این دو نقطه برابر است با:
$${{y_0+\Delta y-y_0} \over {x_0+\Delta x-x_0}}={\Delta y \over \Delta x}$$
از این رو شیب بین دو نقطهِ (x0,y0) و $$(x_0+\Delta x,y_0+\Delta y)$$ برابر با $${\Delta y \over \Delta x}$$ میشود. اما هنوز این مقدار شیب دقیقی را در نقطه (x0,y0) به ما نمیدهد. اگر فاصله دو نقطه را به صفر نزدیک کنیم دقیقا شیب در نقطه مفروض بدست خواهد آمد. بنابراین میتوان گفت شیب در نقطه (x0,y0) برابر است با:
$$\lim_{\Delta x \to 0} {\Delta y \over \Delta x} ={dy \over dx}$$
به عبارت $$dy \over dx$$ مشتق تابع y نسبت به x گفته میشود. این مقدار، تغییرات تابع y را نسبت به متغیر x در یک نقطه خاص، محاسبه میکند. انیمیشن زیر تغییرات شیب با نزدیک شدن به نقطه (x0,y0) را نشان میدهد.
به عملیاتی که در بالا انجام شد، مشتقگیری تابع y نسبت به x گفته میشود.
بنابراین مشتق تابع (y=f(x نسبت به x برابر است با:
$${f'(x)}=\lim_{\Delta x \to 0}{f(x+\Delta x)-f(x)\over \Delta x}={dy \over dx} \enspace \enspace \enspace*$$
در توابع مختلف حاصل این حد حساب شده است.
محاسبه مشتق در توابع مختلف
در این قسمت میخواهیم مشتق چند تابع را بدست آوریم. البته توجه داشته باشید که مواردی که تابع y مستقیما، بهصورت صریح بر حسب x بیان نمیشود، میتوان از مشتقگیری ضمنی استفاده کرد. در مطلب «مشتق ضمنی — به زبان ساده» از مجله فرادرس میتوانید در مورد این روش بیشتر مطالعه کنید.
مثال ۱
مشتق تابع f(x)=x را بدست آورید.
با جایگذاری تابع f در معادله * داریم:
$${f'(x)}=\lim_{\Delta x \to 0}{f(x+\Delta x)-f(x)\over \Delta x}={{x+\Delta x -x} \over {\Delta x}}=1 \enspace \enspace \enspace$$
با توجه به پاسخ بدست آمده شیب این تابع در تمامی نقاطش برابر با ۱ است.
دیگر توابع
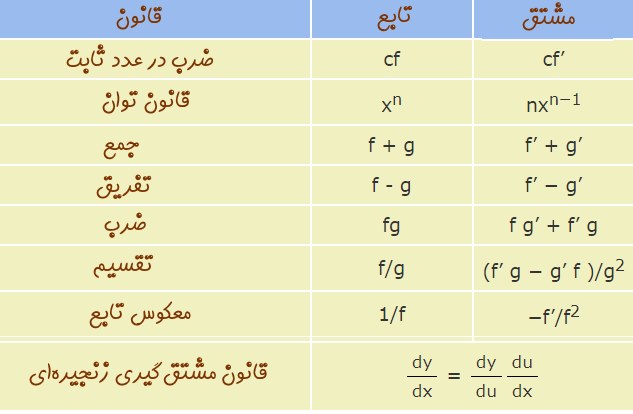
فرض کنید در جلسه امتحان حضور دارید و میخواهید مشتق تابع $$f(x)=xtan(x)$$ را محاسبه کنید. در ابتدا به نظر میرسد بایستی برای قبول شدن در این درس تا سال بعد صبر کنید! اما واقعیت این است که مشتق توابع مختلف را میتوان با استفاده از قوانین حاکم بر آنها پیدا کرد و همواره نیاز نیست تا از طریق معادله * عمل کرد. در جدول زیر حاصل مشتقِ معروفترین توابع موجود در ریاضیات بیان شده است.
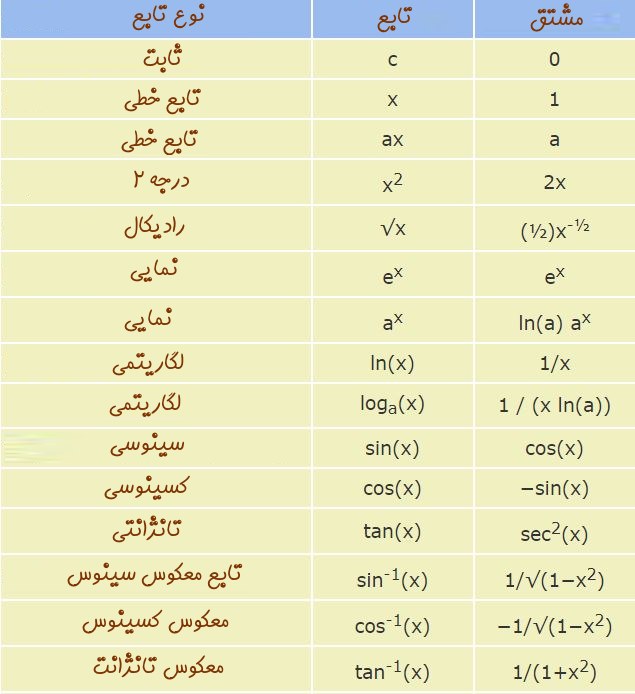
قوانین مشتقگیری
با استفاده از مشتقات توابع معرفی شده در بالا میتوان مشتق هر نوع تابعی را بدست آورد. البته بایستی قوانین حاکم بر مشتق را دانست. برای مثال مشتق تابع $$y=f(x)+g(x)$$ با مشتق $$y=g(x)+y(x)$$ برابر است. در جدول زیر مهمترین قوانین کاربردی در فرآیند مشتقگیری معرفی شدهاند.
اثبات مشتق جمع دو تابع
فرض کنید دو تابع $$ f (x) $$ و $$ g ( x ) $$ داده شدهاند که در نقطهای مانند $$x$$ مشتقپذیر هستند. میخواهیم مشتق اثبات کنیم مشتق جمع دو تابع، یعنی $$ h (x ) = f (x) + g ( x ) $$، برابر با $$h'(x) = f'(x)+g'(x)$$. برای این کار از تعریف مشتق استفاده میکنیم.
$$ \large \begin {align} h'(x) & = \lim _ { a\to 0} \frac{h(x+a)-h(x)}{a} \\
& = \lim_{a\to 0} \frac{[f(x+a)+g(x+a)]-[f(x)+g(x)]}{a} \\
& = \lim_{a\to 0} \frac{f(x+a)-f(x)+g(x+a)-g(x)}{a}
\\
& = \lim_{a\to 0} \frac{f(x+a)-f(x)}{a} + \lim_{a\to 0} \frac{g(x+a)-g(x)}{a} \\
&= f'(x)+g'(x)
\end {align} $$
اثبات مشتق تفریق دو تابع
اثبات مشتق تفریق دو تابع نیز مشابه اثبات مشتق جمع دو تابع است. فرض کنید دو تابع $$ f (x) $$ و $$ g ( x ) $$ داده شدهاند که در نقطهای مانند $$x$$ مشتقپذیر هستند.
میخواهیم مشتق اثبات کنیم مشتق تفریق دو تابع، یعنی $$ h (x ) = f (x) - g ( x ) $$، برابر با $$h'(x) = f'(x)-g'(x)$$. برای این کار از تعریف مشتق استفاده میکنیم.
$$ \large \begin {align} h'(x) & = \lim _ { a\to 0} \frac{h(x+a)-h(x)}{a} \\
& = \lim_{a\to 0} \frac{[f(x+a)-g(x+a)]-[f(x)-g(x)]}{a} \\
& = \lim_{a\to 0} \frac{f(x+a)-f(x)-[g(x+a)-g(x)]}{a}
\\
& = \lim_{a\to 0} \frac{f(x+a)-f(x)}{a} - \lim_{a\to 0} \frac{g(x+a)-g(x)}{a} \\
&= f'(x)-g'(x)
\end {align} $$
اثبات مشتق ضرب دو تابع
فرض کنید $$ h ( x ) = f ( x ) g ( x ) $$ را داشته باشیم. که در آن، $$f$$ و $$g$$ دو تابع مشتقپذیر هستند. میخواهیم اثبات کنیم مشتق $$h$$ برابر با $$ h'(x) =f'(x)g(x)+f(x)g'(x)$$ است.
برای این کار، از تعریف مشتق استفاده میکنیم:
$$ \large \begin{align}
h'(x) &= \lim_{\Delta x\to 0} \frac{h(x+\Delta x)-h(x)}{\Delta x} \\[5pt]
&= \lim_{\Delta x\to 0} \frac{f(x+\Delta x)g(x+\Delta x)-f(x)g(x)}{\Delta x} \\[5pt]
&= \lim_{\Delta x\to 0} \frac{f(x+\Delta x)g(x+\Delta x)-f(x)g(x+\Delta x)+f(x)g(x+\Delta x)-f(x)g(x)}{\Delta x} \\[5pt]
&= \lim_{\Delta x\to 0} \frac{\big[f(x+\Delta x)-f(x)\big] \cdot g(x+\Delta x) + f(x) \cdot \big[g(x+\Delta x)-g(x)\big]}{\Delta x} \\[5pt]
&= \lim_{\Delta x\to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} \cdot {\lim_{\Delta x\to 0} g(x+\Delta x)}
+ \lim_{\Delta x\to 0} f(x) \cdot \lim_{\Delta x\to 0} \frac{g(x+\Delta x)-g(x)}{\Delta x} \\[5pt]
&= f'(x)g(x)+f(x)g'(x).
\end{align} $$
در عملیات بالا، تساوی $$\lim_{\Delta x\to0} g(x+\Delta x) = g(x)$$ طبق قضیهای نوشته شده که بیان میکند توابع مشتقپذیر پیوستهاند.
اثبات مشتق تقسیم دو تابع
میخواهیم تساوی زیر را اثبات کنیم:
$$ \large { h' ( x ) = \frac { g ( x ) \cdot f' ( x ) - f ( x ) \cdot g' ( x ) } { \left ( g ( x ) \right ) ^ 2 } } $$
از تعریف پایه مشتق استفاده میکنیم:
$$ \large \displaystyle \dfrac { d h ( x ) } { d x } = \lim _ { \Delta x \rightarrow 0 } { \frac { h ( x + \Delta x ) - h ( x ) } { \Delta x } } . $$
از آنجا که $$ \frac { f ( x ) } { g ( x ) } = h ( x ) $$ است، میتوان نوشت:
$$ \large \displaystyle \dfrac { d h ( x ) } { d x } = \lim _ { \Delta x \rightarrow 0 } { \dfrac { \frac { f ( x + \Delta x ) } { g ( x + \Delta x ) } - \frac { f ( x ) } { g ( x ) } } { \Delta x } } . $$
عبارت بالا را به صورت زیر ساده میکنیم:
$$ \large \begin {aligned} \frac { d h ( x ) } { d x } & = \lim _ { \Delta x \rightarrow 0 } { \frac { f ( x + \Delta x ) g ( x ) -f ( x ) g ( x + \Delta x ) } { \Delta x g ( x ) g ( x + \Delta x ) } } \\\\ & = \lim _ { \Delta x \rightarrow 0 } { \frac { 1 } { g ( x ) g ( x + \Delta x ) } } \lim _ { \Delta x \rightarrow 0 } { \frac { f ( x + \Delta x ) g ( x ) - f ( x ) g ( x + \Delta x ) } { \Delta x } } \\\\ & = \frac { 1 } { \big ( g ( x ) \big ) ^ 2 } \lim _ { \Delta x \rightarrow 0 } { \frac { f ( x + \Delta x ) g ( x ) -f ( x ) g ( x + \Delta x ) } { \Delta x } } . \end {aligned} $$
با اضافه و کم کردن $$ f (x) g ( x ) $$ در صورت کسر، داریم:
$$ \large \displaystyle \frac { d h ( x ) } { d x } = \frac { 1 } { { \big ( g ( x ) \big ) } ^ { 2 } } \lim _ { \Delta x \rightarrow 0 } { \frac { f ( x + \Delta x ) g ( x ) - f ( x ) g ( x ) + f ( x ) g ( x ) - f ( x ) g ( x + \Delta x ) } { \Delta x } } $$
با اعمال چند تغییر کوچک در عبارت بالا، خواهیم داشت:
$$ \large \begin {aligned} \frac { d h ( x ) } { d x } & = \frac { 1 } { { g ( x ) } ^ { 2 } } \lim _ { \Delta x \rightarrow 0 } { \left ( g ( x ) \bigg ( \frac { f ( x + \Delta x ) - f ( x ) } { \Delta x } \bigg ) - f ( x ) \bigg ( \frac { g ( x + \Delta x ) - g ( x ) } { \Delta x } \bigg ) \right ) } \\\\ & = \dfrac { \displaystyle \left ( g ( x ) \bigg ( \lim _ { \Delta x\rightarrow 0 } { \frac { f ( x + \Delta x ) - f ( x ) } { \Delta x } } \bigg ) - f ( x ) \bigg ( \lim _ { \Delta x \rightarrow 0 } { \frac { g ( x + \Delta x ) -g ( x ) } { \Delta x } } \bigg ) \right) } { { g ( x ) } ^ { 2 } } . \end {aligned} $$
در نهایت، فرمول مورد نظر به دست میآید:
$$ \large \displaystyle { \dfrac { d h ( x ) } { d x } = \dfrac { f' ( x ) g ( x ) - g' ( x ) f ( x ) } { { \big ( g ( x ) \big ) } ^ { 2 } } } . \ $$
در بخش آینده با کاربرد این قوانین در محاسبه مشتق توابع مختلف آشنا خواهید شد.
آزمون مشتق
در این قسمت به منظور درک بهتر مفهوم مشتق، تعدادی پرسش چهار گزینهای به صورت آزمون تهیه شده است.
تابع $$h (z) = 6 + 40 z^ 3 - 5 z^ 4 - 4 z ^ 5 $$ در چه ناحیهای صعودی است؟
تابع $$h ( z ) $$ در ناحیه $$-3 < z < 0 $$ و $$0 < z < 2 $$ صعودی است.
تابع $$h ( z ) $$ در ناحیه $$0 < z < 2 $$ صعودی است.
تابع $$h ( z ) $$ در ناحیه $$-3 < z < 0 $$ صعودی است.
تابع $$h ( z ) $$ در ناحیه $$- \ \infty < z < -3 $$ و $$2 < z < \infty $$ صعودی است.
با استفاده از مشتق میتوانیم نرخ تغییرات توابع مختلف را بهدست آوریم. به هنگام صحبت در مورد صعودی یا نزولی بودن توابع، نرخ تغییرات آنها مد نظر ما است. از اینرو، به مشتق نیاز داریم. از اینرو، برای آنکه بدانیم تابع $$h (z) = 6 + 40 z^ 3 - 5 z^ 4 - 4 z ^ 5 $$ در چه ناحیهای صعودی است، ابتدا مشتق آن را بهدست میآوریم:
$$\begin{equation}
h^{\prime}(z)=120 z^2-20 z^3-20 z^4=-20 z^2(z+3)(z-2)
\end{equation}$$
در ادامه، $$h^{\prime}(z)$$ را برابر صفر قرار میدهیم و مقدارهای z که در آنجا تابع $$h^{\prime}(z)$$ برابر صفر میشود را بهدست میآوریم:
$$\begin{equation}
h^{\prime}(z)=0 \quad \Rightarrow \quad-20 z^2(z+3)(z-2)=0
\end{equation}$$
بنابراین به ازای مقدار صفر، ۲ و ۳- برای z تابع $$h^{\prime}(z)$$ برابر صفر میشود. سپس، برای آنکه بدانیم تابع $$h ( z )$$ در چه نواحی صعودی و در چه نواحی نزولی است، باید بدانیم $$h^{\prime}(z)$$ به ازای چه مقدارهایی از z مثبت و به ازای چه مقدارهایی از z منفی است. مثبت بودن $$h^{\prime}(z)$$ در ناحیهای خاص به معنای صعودی بودن تابع $$h ( z )$$ در آن ناحیه و منفی بودن $$h^{\prime}(z)$$ به معنای نزولی بودن تابع $$h ( z )$$ در ناحیه موردنظر است. از آنجا که $$h^{\prime}(z)$$ تابعی پیوسته است، تنها جایی علامت آن میتواند تغییر کند که $$h^{\prime}(z)$$ برابر صفر باشد. تعیین علامت $$h^{\prime}(z)$$ در تصویر زیر انجام شده است.
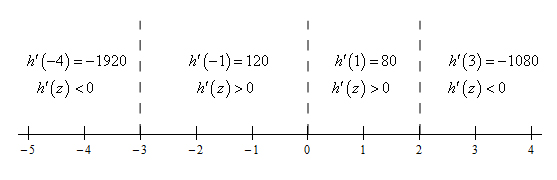
در نتیجه، تابع $$h ( z ) $$ در ناحیه $$-3 < z < 0 $$ و $$0 < z < 2 $$ صعودی است.
خط مماس بر تابع $$f ( x ) = 7 x ^ 4 + 8 x ^ { -6 } + 2x $$ در $$x = -1 $$، کدام یک از گزینههای زیر است؟
$$ y = 22x$$
$$y = 22 x + 35 $$
$$y = 2 x + 35 $$
$$ y = 1 $$
با استفاده از مشتق میتوانیم شیب خط مماس بر توابع مختلف را در نقطههای داده شده بهدست آوریم. در نتیجه، برای بهدست آوردن خط مماس بر تابع $$f ( x ) = 7 x ^ 4 + 8 x ^ { -6 } + 2x $$ در $$x = -1 $$، ابتدا مشتق آن محاسبه میکنیم:
$$\begin{equation}
f^{\prime}(x)=28 x^3-48 x^{-7}+2=28 x^3-\frac{48}{x^7}+2
\end{equation}$$
در ادامه، مقدار تابع و مقدار مشتق آن را در نقطه $$x = -1 $$ بهدست میآوریم:
$$\begin{equation}
f(-1)=7+8-2=13 \quad f^{\prime}(-1)=-28+48+2=22
\end{equation}$$
در پایان، معادله خط مماس را به صورت زیر مینویسیم:
$$\begin{equation}
y=f(-1)+f^{\prime}(-1)(x+1)=13+22(x+1) \quad \rightarrow \quad y=22 x+35
\end{equation}$$
معادله خط مماس بر تابع $$ g ( x ) = \frac { 16 } { x } - 4 \sqrt { x } $$ در $$x = 4 $$ کدام یک از گزینههای زیر است؟
$$y = 2x - 4 $$
$$ y = - 2 x + 4 $$
$$ y = 4 $$
$$ y = - 2 x - 4 $$
با استفاده از مشتق میتوانیم خط مماس بر تابعی مشخص را بهدست آوریم. برای بهدست آوردن خط مماس بر تابع $$ g ( x ) = \frac { 16 } { x } - 4 \sqrt { x } $$ در $$x = 4 $$، ابتدا مشتق تابع را به صورت زیر محاسبه میکنیم:
$$\begin{equation}
g(x)=16 x^{-1}-4 x^{\frac{1}{2}} \quad \Rightarrow \quad g^{\prime}(x)=-16 x^{-2}-2 x^{-\frac{1}{2}}=-\frac{16}{x^2}-\frac{2}{\sqrt{x}}
\end{equation}$$
در ادامه، مقدار تابع و مشتق آن را در $$x = 4 $$ بهدست میآوریم:
$$\begin{equation}
g( 4 )= \frac { 16 } { 4 }- 4 \sqrt { 4 } = -4 \quad \Rightarrow \quad g^{\prime}( 4 )=-16 (4 )^{-2}-2 (4 )^{-\frac{1}{2}}=-\frac{16}{(4 )^2}-\frac{2}{\sqrt{4}} = -2
\end{equation}$$
در نتیجه، معادله خط مماس بر تابع داده شده به صورت زیر نوشته میشود:
$$\begin{equation}
y = g ( 4 ) + g ^ { \prime} ( 4 ) ( x - 4 ) = - 4 - 2 ( x - 4 ) \rightarrow y = - 2 x + 4
\end{equation}$$
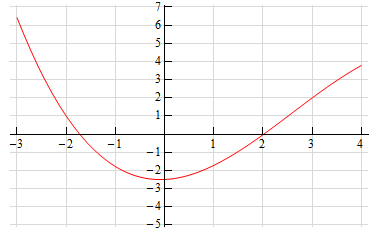
با توجه به نمودار $$f ( x )$$ در تصویر زیر، مقدار $$ f^ { \prime} ( -2 )$$ تقریبا چه مقداری است؟
۲-
۳-
۴-
۱-
همانطور که میدانیم شیب خط مماس بر تابع در هر نقطه، مشتق تابع در آن نقطه را به ما میدهد. بنابراین، برای بهدست آوردن مقدار تقریبی $$ f^ { \prime} ( -2 )$$، خطی مماس بر نمودار $$f ( x ) $$ در نقطه $$x= -2 $$ رسم میکنیم.
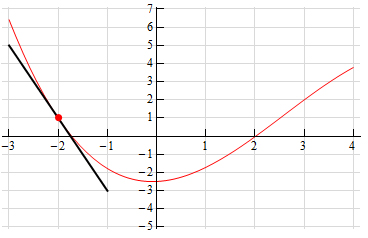
همانطور که در تصویر فوق مشاهده میکنید، نمودار به طور واضح در نقطه $$x= -2 $$ نزولی و مشتق تابع $$f ( x ) $$ در نقطه $$x= -2 $$ منفی است. برای بهدست آوردن مقدار تقریبی $$ f^ { \prime} ( -2 )$$، کافی است شیب خط مماس بر نمودار را در نقطه $$x= -2 $$ را محاسبه کنیم. برای انجام این کار، دو نقطه روی خط مماس را در نظر میگیریم. با توجه به تصویر بالا، اینگونه به نظر میرسد که خط مماس از دو نقطه $$(-2, 1)$$ و $$( -1 , -3 )$$ عبور میکند. در نتیجه، شیب خط مماس برابر است با:
$$m = \frac { y _ 2 - y_ 1 } { x_ 2 - x _ 1 } = \frac { -3 - 1 } { -1 - ( -2 ) } = -4 $$
در نتیجه، مقدار $$ f^ { \prime} ( -2 )$$ برابر ۴- بهدست میآید.
کدام یک از گزینههای زیر در مورد تابع $$Z ( t ) = \sqrt { 3 t - 4 }$$ نادرست است؟
تابع $$ Z (t) $$ در نقطه $$t = 5 $$ افزایش مییابد.
تابع $$ Z (t) $$ در نقطه $$ t = 10 $$ افزایش مییابد.
تابع $$ Z (t) $$ در نقطه $$t = 5 $$ کاهش مییابد.
تابع $$ Z (t) $$ در نقطه $$t = 300 $$ افزایش مییابد.
همانطور که در گزینهها مشاهده میکنید، افزایشی یا کاهشی بودن تابع $$Z ( t) $$ در سه مقدار متفاوت t بررسی شده است. برای آنکه بدانیم کدام گزینه نادرست است، هر یک از گزینهها را جداگانه بررسی میکنیم.
بررسی افزایشی یا کاهشی بودن تابع $$Z ( t ) $$ در $$t = 5 $$
مشتق تابع به ما نرخ تغییر تابع و کاهشی یا افزایشی بودن آن را به ما میدهد. بنابراین، ابتدا مشتق تابع $$Z ( t )$$ را بهدست میآوریم:
$$ Z ( t ) = \sqrt { 3 t - 4 } \\ Z ( t ) = ( 3 t - 4 ) ^ { \frac { 1 } { 3 } } \\ Z ^ { \prime } ( t ) = \frac { 1 } { 2 } ( 3 t -4 ) ^ { - \ \frac { 1 } { 2 } } = \frac { 1 } { 2 \sqrt { 3t -4 } }$$
در ادامه، مقدار ۵ را به جای t در $$Z ^ { \prime } ( t )$$ قرار میدهیم:
$$Z ^ { \prime } ( 5 ) = \frac { 3 } { 2 \sqrt { 11 } } $$
از آنجا که مقدار $$Z ^ { \prime } ( 5 )$$ مثبت است، تابع $$Z ( t) $$ در $$ t = 5 $$ افزایشی یا صعودی خواهد بود.
بررسی افزایشی یا کاهشی بودن تابع $$Z ( t ) $$ در $$ t = 10 $$
در این قسمت، مقدار ۱۰ را به جای t در $$Z ^ { \prime } ( t )$$ قرار میدهیم:
$$Z ^ { \prime } ( 10 ) = \frac { 3 } { 2 \sqrt { 26 } } $$
از آنجا که مقدار $$Z ^ { \prime } ( 10 )$$ مثبت است، تابع $$Z ( t) $$ در $$ t = 10 $$ نیز افزایشی یا صعودی خواهد بود.
بررسی افزایشی یا کاهشی بودن تابع $$Z ( t ) $$ در $$t = 300 $$
در این قسمت، مقدار ۳۰۰ را به جای t در $$Z ^ { \prime } ( t )$$ قرار میدهیم:
$$Z ^ { \prime } ( 300 ) = \frac { 3 } { 2 \sqrt { 896 } } $$
از آنجا که مقدار $$Z ^ { \prime } ( 10 )$$ مثبت است، تابع $$Z ( t) $$ در $$ t = 300 $$ نیز افزایشی یا صعودی خواهد بود.
اگر $$f ( 2 ) = -8 $$ و $$f ^ { \prime } ( 2 ) = 3 $$ و $$g ( 2 ) = 17 $$ و $$ g ^ { \prime } ( 2 ) = -4 $$، مقدار $$ ( f g ) ^ { \prime } ( 2 )$$ چه مقدار است؟
۸۳
۳۸
۸۱
۸۰
مشتق ضرب دو تابع به صورت زیر بهدست میآید:
$$\begin{equation}
(f g)^{\prime}(x)=f^{\prime}(x) g(x)+f(x) g^{\prime}(x)
\end{equation}$$
بر طبق صورت مسئله میخواهیم مقدار $$ ( f g ) ^ { \prime } ( 2 )$$ را بهدست آوریم.
$$\begin{equation}
(f g)^{\prime}(2)=f^{\prime}(2) g(2)+f(2) g^{\prime}(2)
\end{equation}$$
مقدارهای $$f ( 2 ) = -8 $$ و $$f ^ { \prime } ( 2 ) = 3 $$ و $$g ( 2 ) = 17 $$ و $$ g ^ { \prime } ( 2 ) = -4 $$ را در رابطه فوق قرار میدهیم و مقدار $$ ( f g ) ^ { \prime } ( 2 )$$ را بهدست میآوریم.
$$\begin{equation}
(f g)^{\prime}(2)=(3)(17)+(-8)(-4)=83
\end{equation}$$
خط مماس بر نمودار $$f(x)=\tan(x)+9\cos(x)$$ در $$ x = \pi$$ کدام یک از گزینههای زیر است؟
$$y=x-\pi-9 $$
$$y=x-\pi-3 $$
$$ y=x-\pi $$
$$ y=x-9 $$
مشتق تابع در نقطهای مشخص، شیب خط مماس بر تابع را در آن نقطه به ما میدهد. مشتق تابع $$f(x)=\tan(x)+9\cos(x)$$ به صورت زیر نوشته میشود:
$$f'(x)=\sec^2(x)-9 \sin(x)$$
در ادامه، مقدار تابع و مشتق آن را در $$ x = \pi$$ بهدست میآوریم:
$$\begin{equation}
f(\pi)=\tan (\pi)+9 \cos (\pi)=-9 \quad f^{\prime}(\pi)=\sec ^2(\pi)-9 \sin (\pi)=1
\end{equation}$$
شیب خط مماس بر تابع $$f(x)=\tan(x)+9\cos(x)$$ در نقطه $$ x = \pi$$ برابر است با:
$$\begin{equation}
y=f(\pi)+f^{\prime}(\pi)(x-\pi)=-9+(1)(x-\pi) \quad \rightarrow \quad y=x-\pi-9
\end{equation}$$
خط مماس بر تابع $$ f ( x ) = 7 ^ x + 4 e ^ x $$ را در $$x = 0 $$ کدام یک از گزینه زیر است؟
$$y=5.9459 x$$
$$y=5+5.9459 x$$
$$y=5+1.9459 x$$
$$y=5-5.9459 x$$
مشتق تابع در نقطهای مشخص، شیب خط مماس بر تابع را در آن نقطه به ما میدهد. مشتق تابع $$ f ( x ) = 7 ^ x + 4 e ^ x $$ به صورت زیر نوشته میشود:
$$\begin{equation}
f^{\prime}(x)=7^x \ln (7)+4 \mathbf{e}^x
\end{equation}$$
در ادامه، مقدار تابع و مشتق آن را در $$ x = 0 $$ بهدست میآوریم:
$$\begin{equation}
f(0)=5 \quad f^{\prime}(0)=\ln (7)+4=5.9459
\end{equation}$$
شیب خط مماس بر تابع $$ f ( x ) = 7 ^ x + 4 e ^ x $$ در نقطه $$ x = 0 $$ برابر است با:
$$\begin{equation}
y=f(0)+f^{\prime}(0)(x-0)=5+(\ln (7)+4) x=5+5.9459 x
\end{equation}$$
تابع $$A ( t ) = t ^ 2 e ^ { 5 - t } $$ به ازای چه مقادیری از t صعودی است؟
$$0 < t < \infty $$
$$0 < t < 2 $$
$$1 < t < 2$$
$$0 < t < 3 $$
برای آنکه بدانیم تابع $$A ( t ) = t ^ 2 e ^ { 5 - t } $$ در چه ناحیهای صعودی است، ابتدا مشتق آن را بهدست میآوریم:
$$\begin{equation}
A^{\prime}(t)=2 t e ^ { 5 - t } = t e ^ { t -5 } ( 2 - t)
\end{equation}$$
در ادامه، $$A^{\prime}(t)$$ را برابر صفر قرار میدهیم و مقدارهای t که در آنجا تابع $$A^{\prime}(t)$$ برابر صفر میشود را بهدست میآوریم:
$$\begin{equation}
A^{\prime}(t)=0 \quad \Rightarrow \quad te ^ { t-5 } ( 2 - t ) = 0 \rightarrow t = 0. \quad t = 2
\end{equation}$$
بنابراین به ازای مقدار صفر و ۲ برای ف تابع $$A^{\prime}(t)$$ برابر صفر میشود. سپس، برای آنکه بدانیم تابع $$A ( t )$$ در چه نواحی صعودی و در چه نواحی نزولی است، باید بدانیم $$A^{\prime}(t)$$ به ازای چه مقدارهایی از t مثبت و به ازای چه مقدارهایی از t منفی است. مثبت بودن $$A^{\prime}(t)$$ در ناحیهای خاص به معنای صعودی بودن تابع $$ A( t )$$ در آن ناحیه و منفی بودن $$A^{\prime}(t)$$ به معنای نزولی بودن تابع $$A ( t )$$ در ناحیه موردنظر است. از آنجا که $$A^{\prime}(t)$$ تابعی پیوسته است، تنها جایی علامت آن میتواند تغییر کند که $$A^{\prime}(t)$$ برابر صفر باشد. تعیین علامت $$A^{\prime}(t)$$ در تصویر زیر انجام شده است.
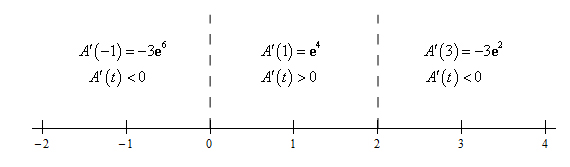
در نتیجه، تابع $$A ( t ) $$ در ناحیه $$0 < t < 2 $$ صعودی است.











میشه اهنگ رو بردارید لططفا
سلام
برای تمرین بیشتر می توانید از دو آموزش زیر در فرادرس که پر از مثال است استفاده کنید.
1- آموزش ریای پایه
2 – آموزش ریاضی یک
مدرس این دو آموزش دکتر شیرافکن است که خیلی ساده مطالب را کفته.
سلام میشه یکی دو تا از مشتق توابع رو با استفاده از فرمول اثبات کنید؟
جیمیل من mahkhorshid95@gmail.com
لطفا جواب سوالمو برام ارسال کنید خیلی ضروریه
ممنون از شما، باعث یاد آوری دروس گذشته ام شد. سپاس🙏🌹
سلام ما سال چهارم دبیرستان یک کتاب ریاضیات داشتیم که ازتون میخوام روی یه جای سایت قرارش بدین بهداشت الان هم با این همه سایت وتکنوولوزوژی کتاب وجزوه نمیدونم چه جوری ازش سر در اوردیم یک دفعه اولین جمله مثل این است که وارد فضا شویم لطفا تعاریف در ریاضیات ومفهوم کلمات خیلی مهم اند ما الان هم در تعاریف کلمات ریاضی مانده ام باید از ریشه به سمت بالا بریم وکرنه مسایل را متوجه نمیشیم ممنون
لطفا در مورد کاربرد مشتق و انتگرال بیشتر توضیح بدین و در صورت امکان از مثال های کاربردی استفاده کنید.
ممنون
سلام عالی بود
درود.
خیلی خوب هست این آموزش و سپاسمندم از شما.
مطالب می تونه ریشه ای تر هم توضیح داده بشه، مثل اثبات ضرب و تقسیم مشتق.
عالی بود واقعاً. ممنون از زحماتتون.
عاااللی
خیلی خوبین ممنون
این یک بحث فلسفی است البته به نظر من.
تعارضات در سازمان یک پیچیدگی درونی است که ریشه در شاکله و دات سازمان ما دارد.
خب حالا اگر بخواهیم شاکله را به زبان ریاضی بیان کنیم. بایستی به قولی اینطور میگو.یند که شاکله به زبان ریاضی انتگرال اعمال ماست و عمل مشتق این شاکله در هر لحظه میباشد. به عنوان ریاضی دان چگونه میتوانید این موضوع را توضیح وتفسیر نمایید که بنده بفهمم. من ریاضی نمیدونم ولی این موضوع مرا درگیر کرده است . مرسی. فیروزیان.
تشکر از خدمت تان
خوب نبود……عالی بود،با تشکر فراوان از سایت فرادرس
چیزایی که سر کلاس مجازی به خوبی یاد نمیگیرم میام توی سایت شما و کاملا درکش میکنم
ممنون فرادرس
سلام
واقعا ممنونم
خیییلی عالییه
بسیار عالی بود.خیلی ممنون
سلام وقت بخیر میشه کمکم کنین؟من دوتا مثال میخوام که مشتق تابع در اون نقطه بشه ½ و -¾…دوتا مثال میخوام ک مشتقشون این بشه خودم نمیتونم بدست بیارم☹
چه نوع تابعی
خداخیرت بده
چند حدیث از پیامبر (ص) در مورد علم
۱-من طلب العلم تکفّل اللَّه برزقه؛ هر که علم جوید خدا عهده دار روزی او شود.
۲- ما تصدّق النّاس بصدقه أفضل من علم ینشر؛ هیچ صدقه ای که مردم دهند از علمی که منتشر شود بهتر نیست.
۳- عالم ینتفع بعلمه خیر من ألف عابد؛ دانشمندی که از علم او سود برند، از هزار عابد بهتر است.
۴- العلم میراثی و میراث الأنبیاء من قبلی؛ علم میراث من و میراث پیامبران پیش از من است.
۵- طلب العلم ساعه خیر من قیام لیله و طلب العلم یوما خیر من صیام ثلاثه أشهر؛ ساعتی علم جستن بهتر از نمازگزاری یک شب است و روزی علم جستن بهتر از سه ماه روزه داری است.
امير المؤمنين على بن ابيطالب عليه السّلام
زکات دانش،نشر آن است.
زكوة العلم نشره
غرر الحکم و درر الکلم، ج 1، ص 52
سلام وقت بخیر ببخشید میشه این سوال x²+25y²=100 مشتق گیری و مشتق ضمنی حل کنید با تشکر
2X=-50Y
(F’x/F’y)= _ (2x/5۰y )_
در صورت y را عددی ثابت در نظر میگیریم و مشتق میگیرم
و در مخرج x را عددی ثابت در نظر میگیریم و مشتق
سپاس گذارم از اموزش خوبتون فقط ی سوال درباره مفهوم مشتق داشتم…
وقتی مشتق یک تابع رو بدست میاریم در واقع داریم شیب مماس در نقطه خاص بدست میاریم اگه اینجوریه پس چرا اونو به کل تابع نسبت میدیم؟؟؟؟ مثلا میگیم مشتق ایکس دو میشه دو ایکس چجوری بجای ی نقطه خاص به کل تابع ما دو ایکسو نسبت میدیم؟؟؟؟
درست است.مشتق در هر نقطه شیب خط مماس در آن نقطه است، هر نقطه مقدار ایکس مربوط به خودش و نیز شیب خط مماس بر خودش را داراست.
اگر در مشتق، ایکس وجود نداشته باشد به این معنی است که مشتق در همه نقاط تابع ثابت است. مثلا مشتق تابع دوایکس(که یک خط راست است) میشود دو.
سلام واقعا ممنونم از اموزشاتتون به خصوص در رشته ریاضیات که بسیار عالی هستن و اقای عوض زاده واقعا بسیار خوب و همه فهم مطالب رو توضیح میدن. اما در مواردی مانند مشتق و حد میتونستن کمی ساده تر مطالب رو بیان کنن. اما باز هم واقعا از سایتتون ممنونم که در پیشرفت تحصیلی شخص بنده کمک موثری بود. واقعا ممنون
با سلام و عرض ادب اگه میشه جزوه ایی از کاربرد ریاضی در اقتصاد هم بزارین ممنون میشم
سلام. میشه در یه پیج دیگه قوانین مشتق رو با استفاده از تعریف مشتق اثبات بکنید. خیلی ممنون از سایت فرادرس عزیز
خیلی عالی بود.
بی نهایت متشکرم
خیلی عالی بود.
سایتتون عالیه
خیلی عالی بود
تشکر از گروه فرادرس . بعد از چند سال جدایی از دانشگاه تصمیم به ادامه تحصیل گرفتم . خیلی از مطالب فراموش شده بود که با استفاده از فیلم ها و مطالب وبلاگ دوباره یاداوری شد.