مختصات کروی — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

در مطالب گذشته، دستگاه مختصات قطبی توضیح داده شد. در این مطلب قصد داریم تا نوعی دیگر از دستگاه مختصات، تحت عنوان مختصات کروی را که در تحلیل‌های سه‌بعدی کاربرد دارد، معرفی کنیم. در مطالب بعدی وبلاگ فرادرس نیز دستگاه مختصات استوانه‌ای مورد مطالعه قرار می‌گیرد.

تعریف مختصات کروی

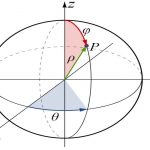
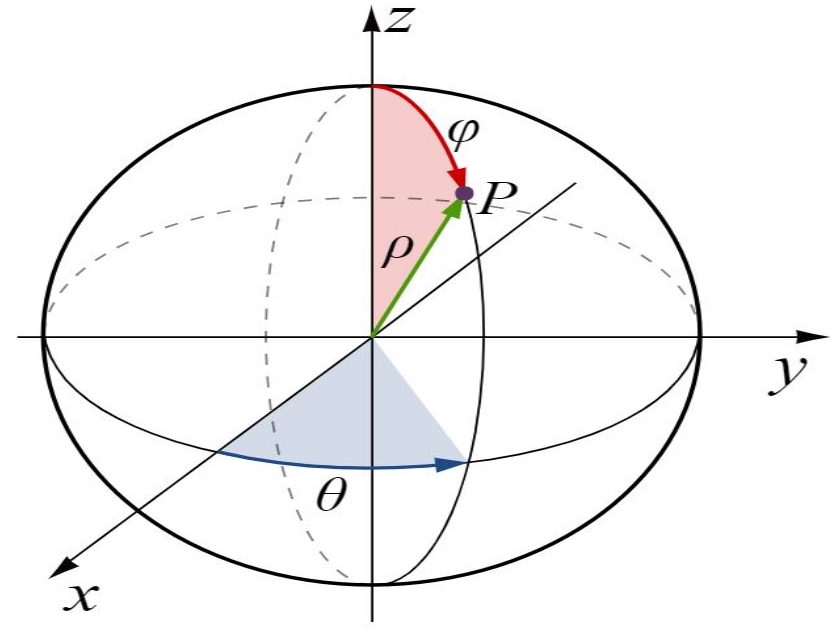
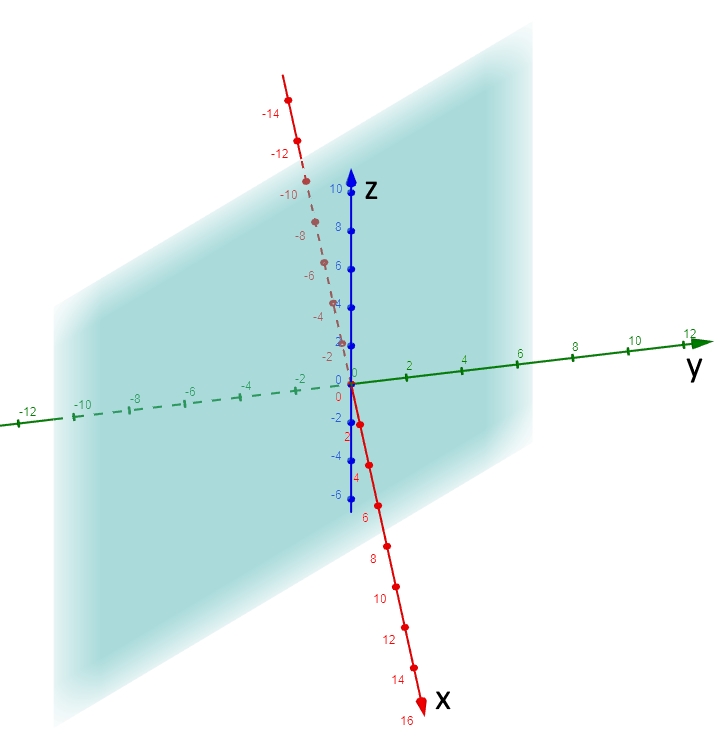
به منظور توصیف یک نقطه در دستگاه مختصات کروی، به سه متغیر نیاز داریم. در ابتدا نقطه‌ای را مطابق با شکل زیر در فضایی سه‌بعدی تصور کنید.

در شکل بالا ρ برابر با فاصله‌ی نقطه از مبدا دستگاه است.

فیلم آموزش هندسه ۲ – پایه یازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

توجه داشته باشید که مقدار ρ همواره بزرگ‌تر یا مساوی صفر در نظر گرفته می‌شود. متغیر دوم θ بوده و اندازه آن برابر با زاویه بین r و جهت مثبت محور x است. توجه داشته باشید که r نشان دهنده تصویر بردارِ نقطه روی صفحه x-y است.

در نهایت مقدار φ برابر با زاویه خط اتصال نقطه به مبدا، با محور z در نظر گرفته می‌شود. توجه داشته باشید که φ در بازه $$0 \le \varphi \le \pi$$ قرار دارد.

بنابراین به طور خلاصه می‌توان گفت، ρ برابر با فاصله نقطه تا مبدا، φ، زاویه خط اتصال نقطه با جهت مثبت محور z و θ معادل با زاویه‌ی تصویر خط اتصال نقطه با محور x است.

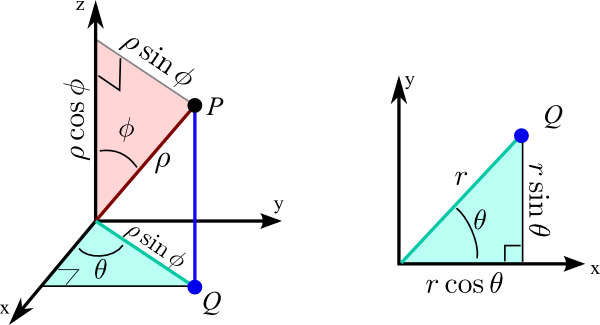
مثلث نشان داده شده در شکل ۱، در ادامه رسم شده است.

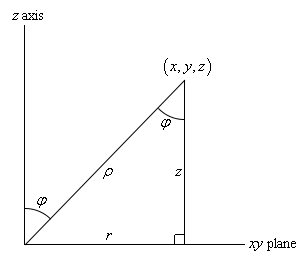
با توجه به تصویر فوق مقادیر z و r را می‌توان به صورت زیر بر حسب φ بیان کرد.

$$\large \begin {align*} z & = \rho \cos \varphi \\ r & = \rho \sin \varphi \end {align*}$$

روابط فوق دقیقا اجزایی هستند که ما به آن‌ها نیاز داریم. بنابراین روابط بین طول‌ها و زاویه φ، به صورت زیر است.

$$\large \begin{align*} r & = \rho \sin \varphi \\ \theta & = \theta \\ z & = \rho \cos \varphi \end {align*}$$
رابطه ۱

از طرفی مختصات‌های دستگاه دکارتی را می‌توان به شکل زیر نیز بیان کرد:

$$\large \begin {align*} x & = r \cos \theta \\ y & = r \sin \theta \\ z & = z \end {align*}$$
رابطه ۲

با توجه به روابط ۱ و ۲، مقادیر x و y و z در دستگاه مختصات کروی برابرند با:

$$\large \begin {align*} x & = \rho \sin \varphi \cos \theta \\ y & = \rho \sin \varphi \sin \theta \\ z & = \rho \cos \varphi \end {align*}$$

همچنین مقدار ρ را می‌توان بر حسب x,y,z نوشت.

$$\large { \rho ^ 2 } = { x ^ 2 } + { y ^ 2 } + { z ^ 2 }$$

مثال ۱

هریک از تبدیل‌های زیر را انجام دهید.

1. نقطه $$\displaystyle \left ( { \sqrt 6 , \frac { \pi } { 4 } , \sqrt 2 } \right )$$ از مختصات استوانه‌ای به کروی
2. نقطه $$\left ( { - 1 , 1 , - \sqrt 2 } \right )$$ از مختصات کارتزینی به کروی

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

(a)

همان‌طور که احتمالا می‌دانید در مختصات استوانه‌ای مختصات به صورت $$( r , \theta , z )$$ بیان می‌شود. بنابراین فاصله نقطه تا مبدا (ρ) برابر است با:

$$\large \rho = \sqrt { { r ^ 2 } + { z ^ 2 } } = \sqrt { 6 + 2 } = \sqrt 8 = 2 \sqrt 2$$

در نتیجه زاویه φ برابر با مقدار زیر بدست می‌آید:

$$\large z = \rho \cos \varphi \hspace {0.25in} \Rightarrow \hspace {0.25in} \cos \varphi = \frac { z } { \rho } = \frac { { \sqrt 2 } } { { 2 \sqrt 2 } } \hspace{0.25in} \Rightarrow \hspace{0.25in} \varphi = { \cos ^ { - 1 } } \left ( { \frac { 1 } { 2 } } \right ) = \frac { \pi } { 3 }$$

نهایتا مختصات نقطه $$\displaystyle \left ( { \sqrt 6 , \frac { \pi } { 4 } , \sqrt 2 } \right )$$ در مختصات کروی به صورت زیر قابل بیان است.

$$\large \left ( { 2 \sqrt 2 , \frac { \pi } { 4 } , \frac { \pi } { 3 } } \right )$$

(b)

فاصله نقطه $$\left ( { - 1 , 1 , - \sqrt 2 } \right )$$ از مبدا، برابر است با:

$$\large \rho = \sqrt { { x ^ 2 } + { y ^ 2 } + { z ^ 2 } } = \sqrt { 1 + 1 + 2 } = 2$$

φ برابر با زاویه خطِ اتصال نقطه با محور z است. بنابراین برای یافتن آن بایستی از مختصات z به صورت زیر استفاده کرد.

$$\large z = \rho \cos \varphi \hspace {0.25in} \Rightarrow \hspace {0.25in} \cos \varphi = \frac { z }{ \rho } = \frac { { - \sqrt 2 } } { 2 } \hspace {0.25in} \Rightarrow \hspace {0.25in} \varphi = { \cos ^ { - 1 } } \left ( { \frac { { - \sqrt 2 } } { 2 } } \right ) = \frac { { 3 \pi } } { 4 }$$

برای بدست آوردن θ، می‌توان از هریک از متغیر‌های x یا y بهره برد. برای نمونه با استفاده از y داریم:

$$ \large \sin \theta = \frac { y } { { \rho \sin \varphi } } = \frac { 1 } { { 2 \left ( { \frac { { \sqrt 2 } } { 2 } } \right ) } } =<br /> \frac { 1 } { { \sqrt 2 } } = \frac { { \sqrt 2 } } { 2 } \hspace {0.5in} \Rightarrow \hspace {0.25in} \theta = \frac { \pi<br /> } { 4 } \, \, { \mbox { or } } \, \,\theta = \frac { { 3 \pi } } { 4 } $$

بنابراین دو انتخاب برای θ وجود دارد. برای انتخاب زاویه صحیح، به مختصات کارتزینی ارائه شده در صورت سوال توجه کنید. همان‌طور که می‌دانید نقطه‌ای با مختصاتِ $$x = - 1$$ و $$y =  1$$ در ربع دوم مختصات قرار می‌گیرد. بنابراین زاویه θ بایستی بین $$\frac { \pi } { 2 }$$ و π قرار داشته باشد. در نتیجه زاویه$$\theta = \frac { { 3 \pi } } { 4 }$$ پاسخ درست مسئله است. نهایتا مختصات نقطه در دستگاه کروی برابر می‌شود با:

$$\large \left ( { 2 , \frac { { 3 \pi } } { 4 } , \frac { { 3 \pi } } { 4 } } \right )$$

در مثال ۱ مختصات یک نقطه در دو دستگاه متفاوت توضیح داده شد. توجه داشته باشید که یک معادله، تابع یا رابطه را نیز می‌توان در دستگاه‌ مختصات‌های متفاوت بیان کرد.

مثال ۲

هریک از توابع زیر چه صفحه‌ای را نشان می‌دهند؟

1. $$\rho = 5$$
2. $$\displaystyle \varphi = \frac { \pi } { 3 }$$
3. $$\displaystyle \theta = \frac { { 2 \pi } } { 3 }$$
4. $$\rho \sin \varphi = 2$$

فیلم آموزش ریاضی پایه – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

(a)

در مبحث معادلات چند متغیره عنوان شد که معادله مربوط به هر صفحه به چه شکل است. بنابراین می‌توان ابتدا معادله را در دستگاه مختصات کارتزینی نوشت و شکل صفحه مربوط به آن را بدست آورد. $$\rho = 5$$ را نیز می‌توان به صورت زیر، در دستگاه کارتزینی نوشت.

$$\large \begin {align*} \rho & = 5 \\ { \rho ^ 2 } & = 2 5 \\ { x ^ 2 } + { y ^ 2 } + { z ^ 2 } & = 2 5 \end {align*}$$

بنابراین $$\rho = 5$$، نشان دهنده کره‌ای به شعاع ۵ و مرکز مبدا مختصات است.

(b)

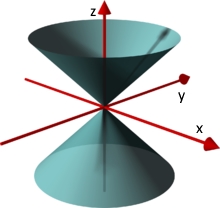
نوشتن معادله $$\displaystyle \varphi = \frac { \pi } { 3 }$$ در دستگاه مختصات کروی مشکل است. این معادله می‌گوید فارغ از فاصله نقطه تا مبدا، زاویه تمامی نقاط با محور z برابر با $$\frac { \pi } { 3 }$$ است. در حقیقت مخروط، صفحه‌ای است که این ویژگی را دارد. همان‌طور که در شکل زیر نیز نشان داده شده، زاویه تمامی نقاط در یک مخروط، با محور z مقداری ثابت است.

(c)

به منظور نوشتن معادله $$\displaystyle \theta = \frac { { 2 \pi } } { 3 }$$ در دستگاه مختصات کروی به ترتیب زیر می‌توان عمل کرد:

$$\large x = \rho \sin \varphi \cos \theta \ \Rightarrow \ x = - \frac { 1 } { 2 } \rho \sin \varphi$$
$$\large y = \rho \sin \varphi \sin \theta \ \Rightarrow \ y = \frac { \sqrt { 3 } } { 2 } \rho \sin \varphi$$

با نوشتن x و y، می‌توان رابطه آن‌ها را نیز به صورت زیر بدست آورد.

$$\large \frac { y } { x } = - \sqrt { 3 } \Rightarrow y = - \sqrt { 3 } x$$

رابطه فوق نشان دهنده صفحه‌ای است که در زاویه $$\displaystyle \theta = \frac { { 2 \pi } } { 3 }$$ نسبت به محور x قرار گرفته است. در شکل زیر این صفحه نشان داده شده است.

(d)

برای بدست آوردن شکل کارتزینی معادله $$\rho \sin \varphi = 2$$، از مفهوم r استفاده می‌کنیم.

$$\large \begin {align*} \rho \sin \varphi & = 2 \\ r & = 2 \end {align*}$$

از طرفی r را می‌توان به شکل زیر نیز بیان کرد:

$$\large \begin {align*} { r ^ 2 } & = 4 \\ { x ^ 2 } + { y ^ 2 } & = 4 \end {align*}$$

رابطه فوق نشان دهنده استوانه‌ای به شعاع 2 است.

در این مطلب مفاهیم پایه‌ای مربوط به مختصات کروی ارائه شد. توجه داشته باشید که معادلات را می‌توان در دستگاه‌های مختصات مختلف بیان کرد. هم‌چنین برای نوشتن یک معادله در دستگاه مختصات کروی بایستی از تبدیل‌های زیر کمک بگیرید.

$$\boxed { \large \begin {align*} x & = \rho \sin \varphi \cos \theta \\ y & = \rho \sin \varphi \sin \theta \\ z & = \rho \cos \varphi \end {align*} }$$

هم‌چنین موقعیت یک نقطه در مختصات کروی به شکل زیر است.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• مجموعه‌ آموزش‌های ریاضی و فیزیک
• مجموعه‌ آموزش‌های دبیرستان و پیش‌دانشگاهی
• مختصات قطبی -- از صفر تا صد
• انتگرال ناسره — به زبان ساده
• انتگرال در مختصات استوانه‌ای -- از صفر تا صد
• مختصات استوانه ای — به زبان ساده

^^