قضایای حد چیست؟ – به زبان ساده + مثال

در ریاضیات و مهندسی مفهوم حد و پیوستگی بسیار مهم و پر کاربرد هستند. به طور کلی مفهوم حد به این صورت است که اگر ورودی‌های تابع را به یک عدد نزدیک کنیم خروجی‌های تابع به کدام عدد نزدیکتر می‌شوند. همچنین در این مطلب از مجله فرادرس انواع حد و روش‌های حل آن‌ها را خواهیم آموخت و همین طور قضایای حد چیست و چند مثال برای درک بهتر این موضوع ارائه خواهد شد. بنابراین، اگر می‌خواهید با قضایای حد و تمامی مباحث مربوط به آن آشنا شوید، این مطلب را حتما تا انتها مطالعه کنید.

قضایای حد چیست؟

اگر با مفهوم حد وپیوستگی و نحوه محاسبه حد یک تابع آشنا نیستید قبل از قضایای حد به مطالعه آن‌ها که در ادامه آمده است بپردازید. در این قسمت به چند نکته کلیدی از روش‌های محاسبه حد اشاره شده است که بعضی به آن‌ها قضایای حد می‌گویند.

در ابتدا لازم است فرض کنیم که حد $$\mathop {\lim }\limits_{x \to a} f\left( x \right)$$ و $$\mathop {\lim }\limits_{x \to a} g\left( x \right)$$ موجود است و c یک عدد ثابت هست.

جداسازی عدد ثابت از حد تابع

می‌توانیم عدد ثابت ضرب شده در تابع را بیرون بکشیم و فقط از تابع حد بگیریم یا برعکس.

$$\mathop {\lim }\limits_{x \to a} \left[ {cf\left( x \right)} \right] = c\mathop {\lim }\limits_{x \to a} f\left( x \right)$$

حد جمع و تفریق توابع

برای محاسبه حد جمع یا تفریق دو تابع فقط کافی است تا حد هر تابع را جداگانه حساب کنیم و سپس حاصل آن‌ها را جمع یا تفریق کنیم. این ویژگی می‌تواند برای بیش از دو تابع به کار گرفته شود.

$$\mathop {\lim }\limits_{x \to a} \left[ {f\left( x \right) \pm g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to a} f\left( x \right) \pm \mathop {\lim }\limits_{x \to a} g\left( x \right)$$

حد ضرب توابع

برای محاسبه ضرب دو یا چند تابع در هم کافی است تا ابتدا حد هر تابع را جداگانه حساب کنید و حاصل آن‌ها را در هم ضرب کنید.

$$\mathop {\lim }\limits_{x \to a} \left[ {f\left( x \right)g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to a} f\left( x \right)\,\,\,\mathop {\lim }\limits_{x \to a} g\left( x \right)$$

حد تقسیم توابع

برای محاسبه حد تقسیم دو تابع نیز باید ابتدا حد صورت و حد مخرج به صورت جداگانه محاسبه شود و بعد حاصل آن‌ها را تقسیم کرد. ذکر این نکته ضروری است که نباید حد در مخرج صفر شود چون مخرج صفر تعریف نشده است.

$$\displaystyle \mathop {\lim }\limits_{x \to a} \left[ {\frac{{f\left( x \right)}}{{g\left( x \right)}}} \right] = \frac{{\mathop {\lim }\limits_{x \to a} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to a} g\left( x \right)}}{\rm{,}}\,\,\,\,\,{\rm{provided }}\,\mathop {\lim }\limits_{x \to a} g\left( x \right) \ne 0$$

حد توابع توان‌دار

در اینجا $$n$$ هر عدد حقیقی می‌تواند باشد (مثبت، منفی، صحیح، کسری، گنگ، صفر و غیره). اگر $$n$$ در اینجا یک عدد صحیح باشد همان ویژگی ضرب حد دو تابع که در قبل اشاره شد را شامل می‌شود. در رابطه زیر n هر عدد حقیقی می‌تواند باشد.

$$\mathop {\lim }\limits_{x \to a} {\left[ {f\left( x \right)} \right]^n} = {\left[ {\mathop {\lim }\limits_{x \to a} f\left( x \right)} \right]^n},\,\,\,\,{}$$

برای مثال فرض کنید $$n=2$$ است، خواهیم داشت:

$$\begin{align*}\mathop {\lim }\limits_{x \to a} {\left[ {f\left( x \right)} \right]^2} & = \mathop {\lim }\limits_{x \to a} \left[ {f\left( x \right)f\left( x \right)} \right]\\ & = \mathop {\lim }\limits_{x \to a} f\left( x \right)\mathop {\lim }\limits_{x \to a} f\left( x \right)\hspace{0.5in}{\mbox{}}\\ & = {\left[ {\mathop {\lim }\limits_{x \to a} f\left( x \right)} \right]^2}\end{align*}$$

این مثال را می‌توان برای هر مقدار صحیحی از $$n$$ تعمیم داد.

حد عدد ثابت

حد یک عدد ثابت، همان عدد ثابت است. در رابطه زیر c هر عدد حقیقی می‌تواند باشد.

$$\mathop {\lim }\limits_{x \to a} c = c.\,\,\,\,$$

حد تابع ثابت

ازجمله دیگر قضایای حد، حد یک تابع ثابت را برابر ورودی آن تابع هست.

$$\mathop {\lim }\limits_{x \to a} x = a$$

مثال اول قضایای حد

حد تابع زیر را در نقطه $$x=-2$$ حساب می‌کنیم.

$$\mathop {\lim }\limits_{x \to - 2} \left( {3{x^2} + 5x - 9} \right)$$

با استفاده از قضیه که در قبل گفته شد حد این تابع را به حد سه تابع تبدیل می‌کنیم و سپس عدد ثابت را در دو تابع اول از حد بیرون می‌آوریم. بنابراین:

$$\begin{align*}\mathop {\lim }\limits_{x \to - 2} \left( {3{x^2} + 5x - 9} \right) & = \mathop {\lim }\limits_{x \to - 2} 3{x^2} + \mathop {\lim }\limits_{x \to - 2} 5x - \mathop {\lim }\limits_{x \to - 2} 9\\ & = 3\mathop {\lim }\limits_{x \to - 2} {x^2} + \mathop {5\lim }\limits_{x \to - 2} x - \mathop {\lim }\limits_{x \to - 2} 9\end{align*}$$

سپس از سایر قضیه‌ها برای محاسبه حد عدد ثابت و حد تواندار استفاده می‌کنیم.

$$\begin{align*}\mathop {\lim }\limits_{x \to - 2} \left( {3{x^2} + 5x - 9} \right) & = 3\mathop {\lim }\limits_{x \to - 2} {x^2} + \mathop {5\lim }\limits_{x \to - 2} x - \mathop {\lim }\limits_{x \to - 2} 9\\ & = 3{\left( { - 2} \right)^2} + 5\left( { - 2} \right) - 9\\ & = - 7\end{align*}$$

نکته: اگر $$p(x)$$ یک چندجمله‌ای باشد آنگاه:

$$\mathop {\lim }\limits_{x \to a} p\left( x \right) = p\left( a \right)$$

مثال دوم قضایای حد

حد تابع زیر را در نقطه $$z=1$$ حساب می‌کنیم.

$$\mathop {\lim }\limits_{z \to 1} \frac{{6 - 3z + 10{z^2}}}{{ - 2{z^4} + 7{z^3} + 1}}$$

مطابق قضیه گفته شده، ابتدا حد صورت و سپس حد مخرج را محاسبه می‌کنیم.

$$\mathop {\lim }\limits_{z \to 1} \frac{{6 - 3z + 10{z^2}}}{{ - 2{z^4} + 7{z^3} + 1}} = \frac{{\mathop {\lim }\limits_{z \to 1} 6 - 3z + 10{z^2}}}{{\mathop {\lim }\limits_{z \to 1} - 2{z^4} + 7{z^3} + 1}}$$

باید اینجا توجه داشته باشیم که حد تابع در مخرج در $$z=1$$ صفر نباشد که خوشبختانه این چنین نیست.

تابع صورت و مخرج چند جمله‌ای  هستند و خیلی راحت می‌توانیم آن‌ها را محاسبه کنیم.

$$\begin{align*}\mathop {\lim }\limits_{z \to 1} \frac{{6 - 3z + 10{z^2}}}{{ - 2{z^4} + 7{z^3} + 1}} & = \frac{{6 - 3\left( 1 \right) + 10{{\left( 1 \right)}^2}}}{{ - 2{{\left( 1 \right)}^4} + 7{{\left( 1 \right)}^3} + 1}}\\ & = \frac{{13}}{6}\end{align*}$$

باید توجه داشت که چون حد مخرج در $$z=1$$ صفر نشد ما توانستیم از این قضایا استفاده کنیم.

مثال سوم قضایای حد و پیوستگی

می‌خواهیم حد تابع زیر را در نقطه $$x=3$$ حساب کنیم.

$$\mathop {\lim }\limits_{x \to 3} \left( { - \sqrt[5]{x} + \frac{{{{\bf{e}}^x}}}{{1 + \ln \left( x \right)}} + \sin \left( x \right)\cos \left( x \right)} \right)$$

تابع فوق ترکیبی از چند تابع پیوسته است که هیچکدام از آن‌ها در $$x=3$$ ناپیوستگی ندارند. بنابراین هر تابع را جدا کرده و با جایگذاری مستقیم  $$x=3$$ ، حد آن را محاسبه می‌کنیم.

$$\begin{align*}\mathop {\lim }\limits_{x \to 3} \left( { - \sqrt[5]{x} + \frac{{{{\bf{e}}^x}}}{{1 + \ln \left( x \right)}} + \sin \left( x \right)\cos \left( x \right)} \right) & = - \sqrt[5]{3} + \frac{{{{\bf{e}}^3}}}{{1 + \ln \left( 3 \right)}} + \sin \left( 3 \right)\cos \left( 3 \right)\\ & = {\rm{8}}{\rm{.1854272743}}\end{align*}$$

مثال چهارم قضایای حد و پیوستگی

می‌خواهیم حد تابع زیر را در نقطه $$x=2$$ حساب کنیم.

$$\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} + 4x - 12}}{{{x^2} - 2x}}$$

اگر در تابع فوق مقدار $$x=2$$ را قرار دهیم خواهیم داشت:

$$\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} + 4x - 12}}{{{x^2} - 2x}} = \frac{0}{0}$$

متوجه می‌شویم که حاصل یک عبارت مبهم و تعریف نشده است پس نمی‌توانیم با جایگذاری مستقیم $$x=2$$ حد تابع را حساب کنیم. نکته‌ای که باید همیشه در نظر داشته باشیم این است که تابع قبل از حدگیری باید ساده شده باشد. در این مثال صورت و مخرج را ساده می‌کنیم.

$$\begin{align*}\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} + 4x - 12}}{{{x^2} - 2x}} & = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {x - 2} \right)\left( {x + 6} \right)}}{{x\left( {x - 2} \right)}}\\ & = \mathop {\lim }\limits_{x \to 2} \frac{{x + 6}}{x}\end{align*}$$

در ساده‌سازی که انجام دادیم توانستیم عبارت $$x-2$$ را در صورت و مخرج از بین ببریم با این کار عاملی که باعث صفر شدن مخرج می‌شد را حذف کردیم و همچنین به اصطلاح رفع ابهام کردیم. حالا می‌توانیم $$x=2$$ را در تابع قرار دهیم و حد آن را محاسبه کنیم.

$$\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} + 4x - 12}}{{{x^2} - 2x}} = \mathop {\lim }\limits_{x \to 2} \frac{{x + 6}}{x} = \frac{8}{2} = 4$$

مثال پنجم قضایای حد و پیوستگی

حد تابع زیر را در نقطه $$h=0$$ محاسبه خواهیم کرد.

$$\mathop {\lim }\limits_{h \to 0} \frac{{2{{\left( { - 3 + h} \right)}^2} - 18}}{h}$$

در این مثال اگر عبارت $$h=0$$ را مستقیم جایگذاری کنیم حاصل آن $$\frac{0}{0}$$ می‌شود که مبهم و تعریف نشده است. سعی می‌کنیم تا صورت کسر را ساده کنیم تا بتوانیم حد این کسر را حساب کنیم.

$$\begin{align*}\mathop {\lim }\limits_{h \to 0} \frac{{2{{\left( { - 3 + h} \right)}^2} - 18}}{h} & = \mathop {\lim }\limits_{h \to 0} \frac{{2\left( {9 - 6h + {h^2}} \right) - 18}}{h}\\ & = \mathop {\lim }\limits_{h \to 0} \frac{{18 - 12h + 2{h^2} - 18}}{h}\\ & = \mathop {\lim }\limits_{h \to 0} \frac{{ - 12h + 2{h^2}}}{h}\end{align*}$$

اکنون می‌توانیم $$h$$ را از صورت فاکتور بگیریم و آن را با مخرج ساده کنیم.

$$\begin{align*}\mathop {\lim }\limits_{h \to 0} \frac{{2{{\left( { - 3 + h} \right)}^2} - 18}}{h} & = \mathop {\lim }\limits_{h \to 0} \frac{{ - 12h + 2{h^2}}}{h}\\ & = \mathop {\lim }\limits_{h \to 0} \frac{{h\left( { - 12 + 2h} \right)}}{h}\\ & = \mathop {\lim }\limits_{h \to 0} \,\, - 12 + 2h = - 12\end{align*}$$

مثال ششم قضایای حد و پیوستگی

حد تابع زیر را در نقطه $$t=4$$ محاسبه می‌کنیم.

$$\mathop {\lim }\limits_{t \to 4} \frac{{t - \sqrt {3t + 4} }}{{4 - t}}$$

در این مثال نیز اگر عبارت $$t=4$$ را مستقیم جایگذاری کنیم حاصل آن $$\frac{0}{0}$$ می‌شود که مبهم و تعریف نشده است. همچنین مانند مثال‌های گذشته نمی‌توانیم ساده‌سازی کنیم. هرگاه در صورت یا مخرج عبارت جذر داشته باشیم می‌توانیم آن را در مزدوج عبارت ضرب کنیم. به اتحاد زیر توجه کنید:

$$\left( {a + b} \right)\left( {a - b} \right) = {a^2} - {b^2}$$

اکنون می‌خواهیم مزدوج صورت را در صورت و مخرج ضرب کنیم، بنابراین:

$$\mathop {\lim }\limits_{t \to 4} \frac{{t - \sqrt {3t + 4} }}{{4 - t}} = \mathop {\lim }\limits_{t \to 4} \frac{{\left( {t - \sqrt {3t + 4} } \right)}}{{\left( {4 - t} \right)}}\,\frac{{\left( {t + \sqrt {3t + 4} } \right)}}{{\left( {t + \sqrt {3t + 4} } \right)}}$$

سپس محاسبات را با توجه به علامت‌ها ادامه می‌دهیم تا کسر ساده شود.

$$\begin{align*}\mathop {\lim }\limits_{t \to 4} \frac{{t - \sqrt {3t + 4} }}{{4 - t}} & = \mathop {\lim }\limits_{t \to 4} \frac{{{t^2} - \left( {3t + 4} \right)}}{{\left( {4 - t} \right)\left( {t + \sqrt {3t + 4} } \right)}}\\ & = \mathop {\lim }\limits_{t \to 4} \frac{{{t^2} - 3t - 4}}{{\left( {4 - t} \right)\left( {t + \sqrt {3t + 4} } \right)}}\end{align*}$$

دقت کنید که عبارت مخرج را داخل پرانتز نگه داشتیم تا بتوانیم وقتی صورت را ساده کردیم با یکدیگر حذفشان کنیم.

$$\mathop {\lim }\limits_{t \to 4} \frac{{t - \sqrt {3t + 4} }}{{4 - t}} = \mathop {\lim }\limits_{t \to 4} \frac{{\left( {t - 4} \right)\left( {t + 1} \right)}}{{\left( {4 - t} \right)\left( {t + \sqrt {3t + 4} } \right)}}$$

برای ساده کردن عبارت $$(4-t)$$ باید یک منفی از آن فاکتور بگیریم تا بتوانیم با عبارت صورت حذفشان کنیم.

$$\begin{align*}\mathop {\lim }\limits_{t \to 4} \frac{{t - \sqrt {3t + 4} }}{{4 - t}} & = \mathop {\lim }\limits_{t \to 4} \frac{{\left( {t - 4} \right)\left( {t + 1} \right)}}{{ - \left( {t - 4} \right)\left( {t + \sqrt {3t + 4} } \right)}}\\ & = \mathop {\lim }\limits_{t \to 4} \frac{{t + 1}}{{ - \left( {t + \sqrt {3t + 4} } \right)}}\\ & = - \frac{5}{8}\end{align*}$$

بعد از این که به اصطلاح رفع ابهام کردیم مقدار $$t=4$$ را جایگذاری کردیم تا حد تابع را بدست آوریم.

اکنون به یک مثال متفاوت در موضوع حد می‌پردازیم.

مثال هفتم قضایای حد و پیوستگی

در این مثال تابع زیر در نقطه $$y=-2$$ ناپیوسته است و دو مقدار مختلف در این نقطه پیدا می‌کند. می‌خواهیم حد این تابع را در $$y=6$$ و $$y=-2$$ بررسی کنیم.

$$g\left( y \right) = \left\{ \begin{align*}{y^2} + 5 & \hspace{0.25in}{\mbox{if }}y < - 2\\ 1 - 3y & \hspace{0.25in}{\mbox{if }}y \ge - 2\end{align*} \right.$$

الف. $$\mathop {\lim }\limits_{y \to 6} g\left( y \right)$$

ب. $$\mathop {\lim }\limits_{y \to - 2} g\left( y \right)$$

پاسخ:

در حل این نوع سوالات همواره باید به محدوه تابع که در آن پیوستگی وجود دارد توجه کرد. برای محاسبه حد تابع در $$y=6$$ قسمت دوم تابع که در این مقدار پیوستگی دارد یعنی $$( 1 - 3y)$$ را فقط باید بررسی کنیم.

$$\begin{align*}\mathop {\lim }\limits_{y \to 6} g\left( y \right) & = \mathop {\lim }\limits_{y \to 6}( 1 - 3y)\\ & = - 17\end{align*}$$

در قسمت (ب) که چالش اصلی سوال است حد تابع در نقطه $$y=-2$$ دقیقا نقطه‌ای است که ناپیوستگی در آن رخ داده است بنابراین نمی‌توان این نقطه را به طور مستقیم در تابع جایگذاری کرد بلکه باید حد چپ و حد راست را برای این نقطه محاسبه کرد. یادآوری این نکته از قسمت قبل حائز اهمیت که اگر حد چپ و حد راست یک تابع موجود بودند و با هم برابر بودند آنگاه حد آن تابع  در نقطه مورد نظر نیز وجود دارد و برابر همان مقدار است.

ابتدا حد تابع در نقطه ۲- از چپ را بررسی می‌کنیم که در قسمت اول تابع یعنی $$({y^2} + 5)$$ قرار می‌گیرد.

$$\begin{align*}\mathop {\lim }\limits_{y \to - {2^ - }} g\left( y \right) & = \mathop {\lim }\limits_{y \to - {2^ - }} ({y^2} + 5)\hspace{0.25in}{\mbox{since }}y \to {-2^ - }{\mbox{ implies }}y < - 2\\ & = 9\end{align*}$$

سپس حد تابع در نقطه ۲- از راست را بررسی می‌کنیم که در قسمت دوم تابع یعنی $$(1-3y)$$ قرار می‌گیرد.

$$\begin{align*}\mathop {\lim }\limits_{y \to - {2^ + }} g\left( y \right) & = \mathop {\lim }\limits_{y \to - {2^ + }} (1 - 3y)\hspace{0.25in}{\mbox{since }}y \to {-2^ + }{\mbox{ implies }}y > - 2\\ & = 7\end{align*}$$

همان‌طور که مشاهده می‌کنید حد چپ و حد راست تابع در نقطه $$y=-2$$  که محل ناپیوستگی تابع بود را حساب کردیم.

$$\mathop {\lim }\limits_{y \to - {2^ - }} g\left( y \right) = 9 \ne 7 = \mathop {\lim }\limits_{y \to - {2^ + }} g\left( y \right)$$

چون حد چپ و حد راست تابع در نقطه $$y=-2$$ با هم برابر نیستند به اصطلاح می‌گوییم حد تابع در این نقطه موجود نیست.

مثال هشتم قضایای حد و پیوستگی

این مثال با اینکه شبیه مثال قبلی است اما با آن تفاوت اساسی دارد. می‌خواهیم حد تابع زیر را در نقطه $$y=-2$$ محاسبه کنیم.

$$\mathop {\lim }\limits_{y \to - 2} g\left( y \right)\hspace{0.25in}{\mbox{where,}}\,\,g\left( y \right) = \left\{ \begin{align*}{y^2} + 5 & \hspace{0.25in}{\mbox{if }}y < - 2\\ 3 - 3y & \hspace{0.25in}{\mbox{if }}y \ge - 2\end{align*} \right.$$

بایدحد چپ و حد راست در نقطه ناپیوسته را حساب کنیم و با هم مقایسه کنیم.

ابتدا حد تابع در نقطه ۲- از چپ را بررسی می‌کنیم که در قسمت اول تابع یعنی $$({y^2} + 5)$$ قرار می‌گیرد.

$$\begin{align*}\mathop {\lim }\limits_{y \to - {2^ - }} g\left( y \right) & = \mathop {\lim }\limits_{y \to - {2^ - }} ({y^2} + 5)\hspace{0.25in}{\mbox{since }}y \to {-2^ - }{\mbox{implies }}y < - 2\\ & = 9\end{align*}$$

سپس حد تابع در نقطه ۲- از راست را بررسی می‌کنیم که در قسمت دوم تابع یعنی $$(3-3y)$$ قرار می‌گیرد.

$$\begin{align*}\mathop {\lim }\limits_{y \to - {2^ + }} g\left( y \right) & = \mathop {\lim }\limits_{y \to - {2^ + }} (3 - 3y)\hspace{0.25in}{\mbox{since }}y \to {-2^ + }{\mbox{ implies }}y > - 2\\ & = 9\end{align*}$$

حد چپ و حد راست در نقطه $$y=-2$$ با هم برابر هستند بنابراین در این تابع با وجود ناپیوستگی در نقطه $$y=-2$$، حد موجود است.

نکته: اگر $$f\left( x \right) \le g\left( x \right)$$ برای هر $$x$$ در بازه $$[a, b]$$ باشد(احتمالا به غیر از نقطه $$x=c$$) و همچنین $$a \le c \le b$$ آنگاه خواهیم داشت:

$$\mathop {\lim }\limits_{x \to c} f\left( x \right) \le \mathop {\lim }\limits_{x \to c} g\left( x \right)$$

این نکته از آنجا ناشی می‌شود که دو تابع خوش‌تعریف هستند (حد چپ و حد راست با هم برابر هستند). این نامساوی به این علت درست است که مقدار c در بازه a و b قرار دارد و همچنین $$f\left( x \right) \le g\left( x \right)$$.

علت اینکه در بالا عبارت (احتمالا به غیر از نقطه $$x=c$$) آمده است این است که این نامساوی فقط باید در اطراف نقطه $$x=c$$ صادق باشد و نه لزوما در خود آن نقطه.

با بسط این نکته می‌توانیم به قضیه زیر یا همان قضیه فشردگی برسیم.

قضیه فشردگی

پس از اینکه آموختیم قضایای حد چیست حالا به بررسی قضیه فشردگی می‌پردازیم. این قضیه که به «قضیه ساندویچ» نیز معروف است.

طبق قضیه فشردگی، برای هر مقداری از x در بازه $$[a, b]$$ (احتمالا به غیر از نقطه $$x=c$$) خواهیم داشت:

$$f\left( x \right) \le h\left( x \right) \le g\left( x \right)$$

همچنین فرض کنید که داشته باشیم:

$$\mathop {\lim }\limits_{x \to c} f\left( x \right) = \mathop {\lim }\limits_{x \to c} g\left( x \right) = L$$

برای $$a \le c \le b$$ آنگاه خواهیم داشت:

$$\mathop {\lim }\limits_{x \to c} h\left( x \right) = L$$

برای درک بهتر قضیه فشردگی به شکل زیر توجه کنید.

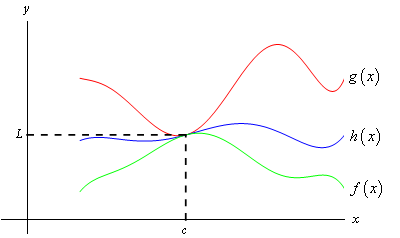
همان‌طور که در شکل فوق می‌بینید اگر حد توابع $$f(x)$$ و $$g(x)$$ در نقطه $$x=c$$ موجود و برابر باشند و تابع $$h(x)$$ که بین آن دو تابع در نقطه $$x=c$$ قرار گرفته است آنگاه حد تابع $$h(x)$$ نیز برابر مقدار آن دو تابع یعنی $$L$$ خواهد شد.

مثال اول قضیه فشردگی

می‌خواهیم حد تابع زیر را در نقطه $$x=0$$ حساب کنیم.

$$\mathop {\lim }\limits_{x \to 0} {x^2}\cos \left( {\frac{1}{x}} \right)$$

برای حل این مثال امکان ساده‌سازی، فاکتورگیری، ضرب مزدوج یا حد چپ و راست وجود ندارد. مشکل دیگری که با آن مواجه هستیم صفر شدن کسر در نقطه $$x=0$$ است.

اولین نکته‌ای که می‌تواند در حل این مثال کمک کند استفاده از مثلثات است.

$$- 1 \le \cos \left( x \right) \le 1$$

سعی می‌کنیم با ضرب عوامل لازم در نامساوی فوق، تابع زیر انتگرال را بسازیم. پس ابتدا نامساوی را معکوس می‌کنیم.

$$- 1 \le \cos \left( {\frac{1}{x}} \right) \le 1$$

سپس نامساوی را در $$x^{2}$$ ضرب می‌کنیم.

$$- {x^2} \le {x^2}\cos \left( {\frac{1}{x}} \right) \le {x^2}$$

در روش فشردگی ما به جای محاسبه حد یک تابع سخت، حد دو تابع آسان‌تر را حساب می‌کنیم. بنابراین حد دو تابع در نامساوی فوق به صورت زیر خواهد بود:

$$\mathop {\lim }\limits_{x \to 0} {x^2} = 0\hspace{0.25in}\hspace{0.25in}\mathop {\lim }\limits_{x \to 0} \left( { - {x^2}} \right) = 0$$

و در نتیجه طبق قضیه فشردگی حد تابع در نقطه $$x=0$$ به شکل زیر است:

$$\mathop {\lim }\limits_{x \to 0} {x^2}\cos \left( {\frac{1}{x}} \right) = 0$$

برای درک بهتر این مثال و روش فشردگی به شکل زیر دقت کنید.

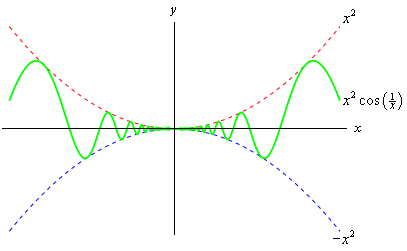
تعریف حد

ابتدا باید با نمادگذاری حد در ریاضیات آشنا شوید.

$$\lim_{x \rightarrow a}f(x)=L$$

در توضیح رابطه بالا موارد زیر را می‌توان اشاره کرد:

• $$lim$$: نماد حد در ریاضی (limit) است.
• $$f(x)$$: تابعی که می‌خواهیم حد آن را محاسبه کنیم.
• $$L$$: مقدار خروجی حد تابع هست.
• $$x\rightarrow a$$: مقدار ورودی تابع وقتی به a نزدیک می‌شود.

این نمادگذاری به این معنا است که ما می‌خواهیم مقدار تابع مورد نظر را در حالی که مقدار ورودی آن به a نزدیک می‌شود را محاسبه کنیم. در واقع خروجی یک تابع را در حدود آن مورد بررسی قرار می‌دهیم. به شکل زیر توجه کنید تا بهتر متوجه شوید:

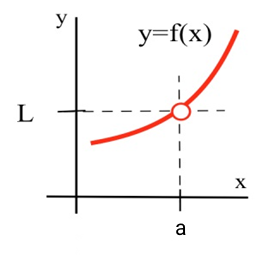
در شکل فوق به اصطلاح می‌گوییم که حد تابع $$f(x)$$ در نقطه $$x=a$$ به $$L$$ میل می‌کند.

اکنون با یک مثال ساده به توضیح بیشتر مفهوم حد می‌پردازیم و حالت‌های متفاوتی را بررسی می‌کنیم.

با توجه به شکل زیر می‌خواهیم مقادیر زیر را حساب کنیم.

1. $$\lim\limits_{x\to 1} f(x)$$
2. $$\lim\limits_{x\to 2} f(x)$$
3. $$\lim\limits_{x\to 3} f(x)$$
4. $$\lim\limits_{x\to 4} f(x)$$

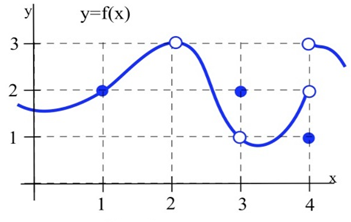
• در مورد اول وقتی x خیلی به سمت ۱ میل می‌کند حد تابع $$f(x)$$ به سمت $$y=2$$ می‌رود. البته باید به توجه کنیم که $$\lim\limits_{x\to 1} f(x)=2$$ با $$f(1) = 2$$ برابر نیست و هدف ما در حدگیری بررسی رفتار تابع در محدود خروجی آن است نه مقدار دقیق آن
• در مورد دوم، مقدار تابع $$f(2)$$ تعریف نشده است، اما ما در حدگیری می‌خواهیم رفتار تابع به ازای $$x=2$$ را در محدوده ۳ بررسی کنیم بنابراین اگر ورودی تابع به مقدار ۲ نزدیک شود خروجی تابع به مقدار ۳ میل می‌کند.
• در مورد سوم، وقتی x به مقدار ۳ نزدیک می‌شود خروجی تابع به ۱ میل می‌کند. این در حالی است که مقدار حقیقی تابع $$f(3) = 2$$ است ولی همان‌طور که در قبل اشاره شد، در حدگیری هدف بررسی رفتار خروجی تابع در محدوده آن است.
• در مورد چهارم، شرایط کمی متفاوت هست. اگر ورودی تابع کمی از ۴ کوچکتر باشد ( یا بگوییم از سمت چپ به x نزدیک می‌شویم) آنگاه مقدار حد تابع برابر ۲ است. ولی اگر ورودی تابع کمی از ۴ بزرگتر باشد ( یا بگوییم از سمت راست به x نزدیک می‌شویم) آنگاه مقدار حد تابع برابر ۳ می‌تواند باشد. در این شرایط چون حد تابع دو مقدار مختلف است به اصطلاح می‌گوییم که حد تابع موجود نیست. باید توجه کنید که پاسخ $$f(4) = 1$$ نیز یه دلایل گفته شده درست نیست.

در این مثال ساده اندکی با مفهوم حد و همسایگی آشنا شدید در ادامه به معرفی دقیق‌تری از همسایگی می‌پردازیم.

همسایگی چیست؟

در حدگیری هدف مقدار خروجی تابع در محدود آن است بنابراین چهار نوع همسایگی را می‌توان تعریف کرد:

• همسایگی یک نقطه: اگر $$x_{\circ}$$ یک عدد حقیقی باشد، هر بازه باز $$(a,b)$$ شامل $$x_{\circ}$$ را یک همسایگی $$x_{\circ}$$ می‌نامیم. به عبارت دیگر اگر $$x_{\circ}\in(a,b)$$ باشد آنگاه بازه باز $$(a,b)$$ شامل $$x_{\circ}$$ است.
• همسایگی محذوف: اگر $$x_{\circ}$$ را از بازه باز $$(a,b)$$ حذف کنیم، آنگاه مجموعه $$(a,b)-\left\{x_{\circ}\right\}$$ را همسایگی محذوف $$x_{\circ}$$ می‌گوییم. به عبارت دیگر همسایگی محذوف یک نقطه اجتماع دو مجموعه به شمار می‌آید.

$$(a,b)-\left\{x_{\circ}\right\}=(a,x_{\circ})\cup(x_{\circ},b)$$

• هماسیگی راست: اگر $$r>0$$ باشد در این صورت بازه $$[x_{\circ},x_{\circ}+r)$$ را یک همسایگی راست نقطه $$x_{\circ}$$ می‌گوییم.
• همسایگی چپ: اگر $$r>0$$ باشد در این صورت بازه $$(x_{\circ}-r,x_{\circ}]$$ را یک همسایگی چپ نقطه $$x_{\circ}$$ می‌گوییم.

اکنون می‌توانیم تعریف دقیق‌تری از حد ارائه کنیم:

$$\lim_{x \rightarrow a}f(x)=L$$

به ازای هر $$\epsilon>0$$ مقداری از $$\delta>0$$ وجود دارد که اگر x به اندازه $$\delta$$ به a نزدیک شود یعنی $$(\mid x-a\mid<\delta)$$، آنگاه مقدار $$f(x)$$ نیز می‌تواند در فاصله $$\epsilon$$ از $$L$$ قرار بگیرد به عبارت دیگر $$(\mid f(x) - L\mid<\epsilon)$$. در ادامه به توضیح ساده از این تعریف می‌پردازیم.

$$\mid x-a\mid$$ یعنی فاصله x از $$a$$. اگر x را خیلی به $$a$$ نزدیک کنیم، فاصله آن‌ها بسیار کم خواهد شد به طوریکه این فاصله از هر عدد حقیقی مثبتی $$\delta$$ کمتر خواهد شد و در نتیجه به صفر نزدیک می‌شود.

$$\mid x-a\mid<\delta$$

$$\mid f(x) - L\mid$$ یعنی فاصله $$f(x)$$ از $$L$$. اگر $$f(x)$$ را خیلی به $$L$$ نزدیک کنیم، فاصله آن‌ها بسیار کم خواهد شد به طوریکه این فاصله از هر عدد حقیقی مثبتی $$\epsilon$$ کمتر خواهد شد و در نتیجه به صفر تمایل پیدا می‌کند.

$$\mid f(x) - L\mid<\epsilon$$

مثال اول همسایگی

در این مثال می‌خواهیم مقدار حد تابع را با عدد گذاری در یک جدول و همینطور بار دیگر با استفاده از انحادهای جبری محاسبه کنیم.

$$\lim_{x \rightarrow 1}\frac{2x^{2}-x-1}{x-1}$$

ممکن است که ابتدا سعی کنید به جای x در تابع عدد ۱ را قرار دهید و حد را محاسبه کنید اما بلافاصله متوجه می‌شوید که مخرج کسر صفر می‌شود و کسر به صورت تعریف نشده در می‌آید.

در جدول زیر از مجله فرادرس مقادیر کمتر از یک را به تابع عدد می‌دهیم تا به اصطلاح حد راست تابع را محاسبه کنیم.

اکنون به تابع مقادیر بیشتر از یک را می‌دهیم تا به اصطلاح حد راست تابع را بدست آوریم

تابع $$f$$ در نقطه $$x=1$$ تعریف نشده است ولی وقتی نزدیک به ۱ می‌شود، مقدار حدی تابع بسیار به عدد ۳ نزدیک خواهد شد.

اکنون می‌خواهیم با استفاده از اتحادهای جبری همین مثال را با روش دیگری حل کنیم:

$$f(x)= \dfrac{2x^2-x-1}{x-1} = \dfrac{(2x+1)(x-1)}{(x-1)} = 2x+1\nonumber$$

همان‌طور که مشاهده می‌کنید صورت کسر را به صورت یک اتحاد دوجمله‌ای درآوردیم که بتوانیم آن را با مخرج ساده کنیم. حالا اگر x به سمت ۱ نزدیک شود حد تابع به سمت ۳ تمایل پیدا می‌کند.

اگر همین تابع یعنی $$y=f(x)= \dfrac{2x^2-x-1}{x-1}$$ را رسم کنیم می‌توانید بهتر درک کنید.

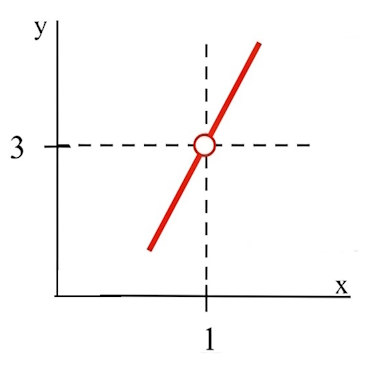
با توجه به شکل فوق متوجه می‌شوید که هرگاه x به ۱ نزدیک می‌شود مقدار تابع نزدیک به ۳ است ولی خود عدد ۳ تعریف نشده است.

مثال اول حد

حد تابع زیر را وقتی x به ۳ تمایل پیدا می‌کند را محاسبه کنید.

$$\lim \limits_{x\to 3} \dfrac{\frac{1}{x} -\frac{1}{3} }{x-3}$$

همان‌طور که می‌دانید تابع در $$x=3$$ تعریف نشده است. با گرفتن مخرج مشترک از دو کسر موجود در صورت به عبارت زیر می‌رسیم:

$$\frac{\frac{1}{x} -\frac{1}{3} }{x-3} = \frac{\frac{1}{x} \cdot \frac{3}{3} -\frac{1}{3} \cdot \frac{x}{x} }{x-3} = \frac{\frac{3}{3x} -\frac{x}{3x} }{x-3} =\frac{\frac{3-x}{3x} }{x-3} \nonumber$$

سپس صورت را در صورت و مخرج را در مخرج به صورت زیر ضرب می‌کنیم:

$$\frac{\frac{3-x}{3x} }{x-3} =\frac{\frac{3-x}{3x} }{\frac{x-3}{1} }\nonumber$$

به صورت معادل داریم:

$$\frac{3-x}{3x} \cdot \frac{1}{x-3}\nonumber$$

با ساده‌سازی بیشتر، یک ۱- را باید از صورت فاکتور بگیریم تا بتوانیم با جمله $$x-3$$ در مخرج ‌آن را ساده کنید.

$$\dfrac{-1(x-3)}{3x} \cdot \dfrac{1}{x-3} =\dfrac{-1}{3x}$$

اکنون می‌توانیم حد را نقطه ۳ محاسبه کنیم:

$$\lim\limits_{x\to 3} \frac{\frac{1}{x} -\frac{1}{3} }{x-3} = \lim\limits_{x\to 3} \frac{-1}{3x} = -\frac{1}{9} \nonumber$$

حد چپ و حد راست

همان طور که در مثال قبل ملاحظه کردید حد بعضی از توابع را باید در چپ و راست (یعنی کمی کمتر و کمی بیشتر ) نقطه ورودی بررسی کرد چون در خود آن نقطه حد تابع تعریف نشده است.

• تعریف حد چپ: حد تابع $$f(x)$$ وقتی $$x$$ به $$c$$ نزدیک می‌شود برابر $$L$$ خواهد بود. اگر مقدار تابع $$f(x)$$ به $$L$$ میل کند زمانی که $$x$$ از سمت چپ به $$c$$ نزدیک خواهد شد $$(x$$ و به صورت زیر این را می‌توانیم بنویسیم:

$$\lim\limits_{x\to c^-} f(x)=L.\nonumber$$

به بیان ساده‌تر وقتی ورودی تابع از چپ (کمتر از مقدار c) باشد آنگاه حدود خروجی تابع $$L$$ می‌تواند باشد.

• تعریف حد راست: حد تابع $$f(x)$$ وقتی $$x$$ به $$c$$ نزدیک می‌شود برابر $$L$$ خواهد بود. اگر مقدار تابع $$f(x)$$ به $$L$$ میل کند زمانی که $$x$$ از سمت راست به $$c$$ نزدیک خواهد شد$$(x>c)$$ و به صورت زیر این را می‌توانیم بنویسیم:

$$\lim\limits_{x\to c^+} f(x)=L.\nonumber$$

به عبارت دیگر وقتی ورودی تابع از راست (بیشتر از مقدار c) باشد آنگاه حدود خروجی تابع $$L$$ می‌شود.

مثال اول حد چپ و حد راست

مطابق شکل زیر می‌خواهیم حد تابع $$f(x)$$ را در $$x=0$$ و $$x=1$$ محاسبه کنیم.

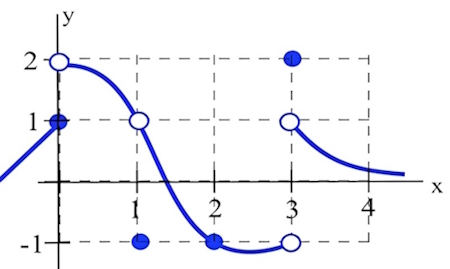
همان‌طور که از شکل پیدا است وقتی x از سمت چپ به صفر نزدیک می‌شود مقدار تابع به ۱ میل می‌کند یعنی:

$$\lim\limits_{x\to 0^-} f(x) = 1.$$

همینطور وقتی x از سمت راست به صفر نزدیک خواهد شد مقدار تابع به ۲ میل می‌کند یعنی:

$$\lim\limits_{x\to 0^+} f(x) = 2.$$

همچنین اگر x از هر طرف به عدد ۱ نزدیک شود حد تابع برابر عدد ۱ خواهد شد. بنابراین:

$$\lim\limits_{x\to 1^-} f(x) = \lim\limits_{x\to 1^+} f(x) = \lim\limits_{x\to 1} f(x) = 1. \nonumber$$

پیوستگی

برای درک بهتر قضایای حد چیست، باید مفهوم پیوستگی را بدانید. یک تابع را به اصطلاح «خوش‌تعریف» می‌نامند اگر هیچ‌گونه شکستگی یا قطعی در نقطه مورد نظر وجود نداشته باشد و پیوسته باشد.

تعریف پیوستگی: تابع $$f(x)$$ در $$x=a$$ پیوسته است اگر و فقط اگر $$\lim\limits_{x\to a} \mathbf{f(x)} = \mathbf{f(a)}$$ باشد.

نمودار زیر نمایانگر رفتار مختلف تابع در نزدیکی نقاط مورد نظر است.

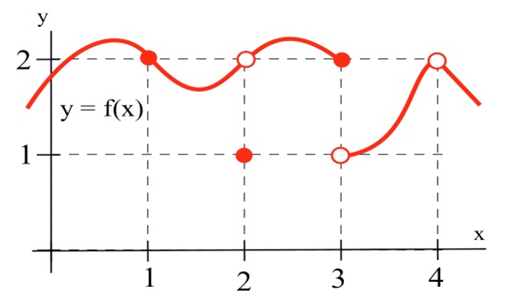
جدول زیر نیز اطلاعات عددی مربوط به همین تابع را نشان داده است.

بنابر اطلاعاتی که از شکل و جدول فوق بدست می‌آید تابع $$f$$در نقطه ۱ و اطراف آن پیوسته است بنابراین:

$$\lim\limits_{x\to 1} f(x) = 2 = f(1)$$

همچنین می‌توان نتیجه گرفت که تابع $$f$$ در نقاط ۲، ۳ و ۴ پیوسته نیست بنابراین:

$$\lim\limits_{x\to 2} f(x) \neq f(2)$$

$$\lim\limits_{x\to 2} f(x) \neq f(2)$$

$$\lim\limits_{x\to 4} f(x) \neq f(4)$$

رفتار تابع در نقاط $$x=2$$ و $$x=4$$ نشان دهنده یک نطقه در گراف است که گاهی اوقات به آن ناپیوستگی در یک نقطه یا ناپیوستگی رفع شدنی گویند زیرا تابع با با تغییر یک مقدار عددی در نقطه می‌تواند پیوسته شود. رفتار تابع در نقطه $$x=3$$ را به اصطلاح ناپیوستگی جهشی گویند زیرا مقدار تابع در این نقطه به طور ناگهانی بین دو مقدار متفاوت دچار تغییر (جهش) شده است.

چه توابعی پیوسته هستند؟

تابع اگر در نقطه مورد نظر تعریف شده باشد، پیوسته به شمار می‌آید. توابعی مانند چندجمله‌ای، جذری، کسری، نمایی و لگاریتمی اگر در نقطه مورد نظر تعریف شده باشند، پیوسته هستند. همچنین هر نوع ترکیبی از توابع پیوسته نیز پیوسته خواهد بود. توضیح تکمیلی در زیر را مطالعه کنید.

• همه چند جمله‌ای‌ها برای هر مقدار x پیوسته هستند.
• توابع کسری، در صورت و مخرج برای هر مقدار x پیوسته هستند به جز نقطه‌ای که مخرج را صفر می‌کند.
• توابع $$\sin (x)$$ و $$\cos (x)$$ برای هر مقدار x پیوسته هستند.
• توابع $$\tan (x)$$ و $$\sec (x)$$ برای هر مقدار x پیوسته هستند به جز $$x \ne \ldots , - \frac{{5\pi }}{2}, - \frac{{3\pi }}{2},\frac{\pi }{2},\frac{{3\pi }}{2},\frac{{5\pi }}{2}, \ldots$$.
• توابع $$\cot (x)$$ و $$\csc (x)$$ برای هر مقدار x پیوسته هستند به جز $$x \ne \ldots , - 2\pi ,\,\, - \pi ,\,\,0,\,\,\pi ,\,\,2\pi , \ldots$$.
• تابع $$\sqrt[n]{x}$$ برای هر x که n فرد باشد پیوسته می‌تواند باشد.
• تابع $$\sqrt[n]{x}$$ برای هر $$x \ge 0$$ که n نیز زوج باشد پیوسته است.
• توابع $${a^x},\,\,{{\bf{e}}^x}$$ برای هر مقدار x پیوسته هستند.
• توابع $${\log _b}x,\,\,\,\ln x$$  برای هر $$x>0$$ پیوسته هستند. توجه داشته باید که لگاریتم فقط مقادیر مثبت را می‌پذیرد.

تعریف پیوستگی تابع به ما کمک می‌کند تا حد آن تابع را اگر در نقطه مورد نظر پیوسته باشد با جایگذاری مستقیم محاسبه کنیم.

مثال اول حد و پیوستگی

می‌خواهیم حد توابع زیر را با استفاده از پیوستگی بدست آوریم.

1. $$\lim\limits_{x\to 2} x^3-4x$$
2. $$\lim\limits_{x\to 2} \dfrac{x-4}{x+3}$$
3. $$\lim\limits_{x\to 2} \dfrac{x-4}{x-2}$$

پاسخ:

• در مورد اول تابع یک چندجمله‌ای است که برای هر مقداری از x تعریف شده است، بنابراین می‌توانیم حد تابع را با جایگذاری مستقیم حل کنیم.

$$\lim\limits_{x\to 2} x^3-4x = 2^3-4(2) = 0. \nonumber$$

• در مورد دوم یک تابع کسری است که در نقطه $$x=-3$$ تعریف نشده است ولی در نقطه ۲ و اطراف آن تعریف شده است بنابراین می‌توانیم حد تابع را با جایگذاری مستقیم حل کنیم.

$$\lim\limits_{x\to 2} \dfrac{x-4}{x+3} = \dfrac{2-4}{2+3}= -\dfrac{2}{5}. \nonumber$$

• در مورد سوم که یک تابع کسری است، تابع در نقطه $$x=2$$ تعریف نشده و همینطور ناپیوسته است. بنابراین نمی‌توانیم حد تابع را با جایگذاری مستقیم حل کنیم.

جمع‌بندی قضایای حد

حد در ریاضی نقشی اساسی در زمینه‌های مختلف از جمله حساب دیفرانسیل، تحلیل و آمار ایفا می‌کند. حد یک چارچوب ریاضی را برای درک رفتار توابع ارائه می‌دهد زیرا ورودی آنها به مقادیر خاص یا بی نهایت نزدیک می‌شود. در این مطلب از مجله فرادرس با مفهوم حد، روش‌های محاسبه حد و قضایای حد چیست آشنا شدید همچنین با استفاده از قضیه فشردگی یک روش منحصر بفرد برای حل حد برخی توابع دشوار را آموختید. با درک حد و پیوستگی، می توانیم بینش عمیق‌تری در مورد رابطه بین توابع و چگونگی تغییر آنها در طول زمان به دست آوریم.