توابع صعودی و نزولی — به زبان ساده

در آموزش‌های پیشین مجله فرادرس، درباره مفاهیم تابع و موضوعات مرتبط با آن بحث کردیم. در این آموزش‌ها، با مباحثی چون دامنه و برد تابع، تابع یک به یک و پوشا، معکوس تابع، ترکیب توابع، توابع زوج و فرد و توابع چندمتغیره آشنا شدیم. اکنون، یکی از مشخصه‌های مهم توابع و نحوه تعیین آن را ارائه می‌کنیم. این ویژگی، صعودی یا نزولی بودن توابع است.

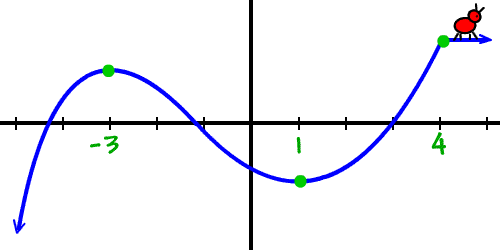
ابتدا مفهوم ساده شهودی این مفاهیم را ارائه می‌کنیم. نمودار تابع زیر را در نظر بگیرید:

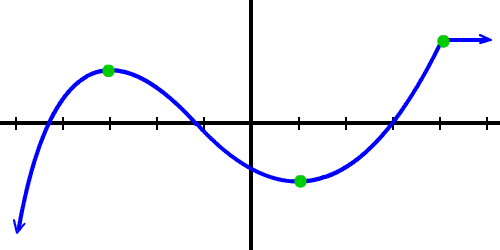
مورچه‌ای را در نظر بگیرید که می‌خواهد این منحنی را بپیماید. همان‌طور که می‌دانیم، جهت قراردادی محور افقی یا همان محور x به سمت راست است. بنابراین، فرض می‌کنیم مورچه فقط از چپ به راست حرکت می‌کند.

اگر مورچه از جایی بالا برود (صعود کند)، آن قسمت از نمودار، صعودی یا افزایشی است.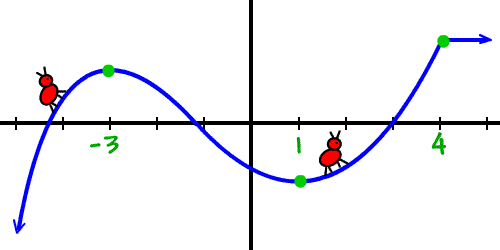

بنابراین، نمودار بالا در بازه‌های زیر صعودی است:

اگر مورچه از جایی پایین بیاید، آن بخش از نمودار، نزولی یا کاهشی است.

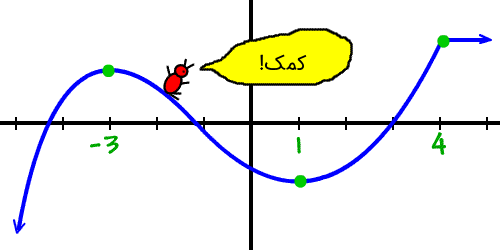
بنابراین، نمودار در بازه زیر نزولی است:

دقت کنید که بازه را به‌صورت بسته زیر ننوشتیم:

چون در نقاط $$-3$$ و 1، وضعیت متفاوت است. وقتی مورچه روی نقطه x=3 نمودار بایستد، چه می‌توان گفت؟ این نقطه، نه صعودی است و نه نزولی.

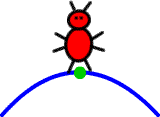
اگر مورچه در بازه $$(4, \infty)$$ قدم بزند چه اتفاقی رخ می‌دهد؟ در این بازه، یک خط افقی (با شیب صفر) وجود دارد و مورچه بالا یا پایین نمی‌رود. بنابراین، نمودار در این قسمت، نه صعودی و نه نزولی است.

در ادامه، تعاریف و نحوه تعیین صعودی و نزولی بودن توابع را بیان خواهیم کرد.

توابع صعودی

به بیان ساده، یک تابع، «صعودی» (Increasing) است، اگر مقدار y با افزایش مقدار x، زیاد شود.

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

شکل زیر این موضوع را نشان می‌دهد.

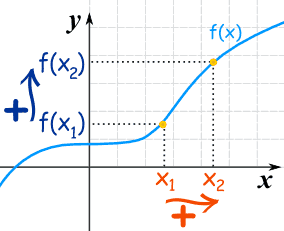
از شکل بالا می‌توان دید که با حرکت در جهت محور x، مقدار $$y(x)$$ افزایش می‌یابد. اما اگر به شکل دقت کنید، ممکن است پرسشی در ذهنتان ایجاد شود و آن این است که در مورد بخش صاف یا تخت نمودار که نزدیک محور y است چه می‌توان گفت؟ آیا باز هم می‌توان گفت که تابع صعودی است؟ بله. این تابع صعودی است. اما در این حالت نمی‌توانیم بگوییم تابع «اکیداً صعودی» (Strictly Increasing) است.

تعریف: تابع $$y=f(x)$$ را صعودی گوییم، اگر وقتی $$x_1$$، آن‌گاه $$f(x_1)\le f(x_2)$$ باشد. همچنین، تابع $$y=f(x)$$ را اکیداً صعودی گوییم، اگر، وقتی $$x_1$$، آن‌گاه $$f(x_1)< f(x_2)$$ باشد.

در تعریف بالا، به علامت‌های > و $$\le$$ دقت کنید.

تابع زیر، یک تابع صعودی است که نرخ صعود آن در حال کاهش است.

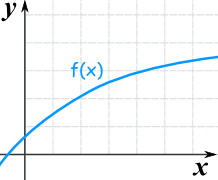
گاهی تنها نیاز داریم تابع را در یک بازه بررسی کنیم. برای مثال، تابع شکل زیر در بازه مشخص‌ شده صعودی است.

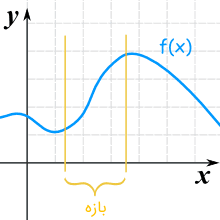
تابع نزولی

به بیان ساده، یک تابع، «نزولی» (Decreasing) است، اگر در آن، مقدار y با افزایش مقدار x، کم شود. شکل زیر این موضوع را نشان می‌دهد.

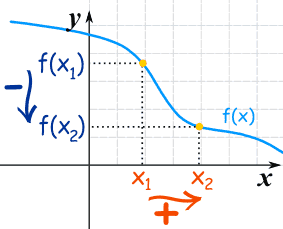
تعریف: تابع $$y=f(x)$$ را نزولی گوییم، اگر وقتی $$x_1$$، آن‌گاه $$f(x_1)\ge f(x_2)$$ باشد. همچنین، تابع $$y=f(x)$$ را اکیداً نزولی گوییم، اگر، وقتی $$x_1$$، آن‌گاه $$f(x_1)> f(x_2)$$ باشد.

مثال 1

می‌خواهیم ببینیم تابع زیر در بازه $$[-1,2]$$ صعودی است یا نزولی.

فیلم آموزش ریاضی 3 – پایه دوازدهم علوم تجربی در فرادرس

کلیک کنید

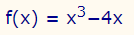
نمودار تابع در شکل زیر نشان داده شده است:

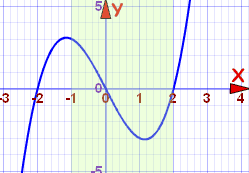
همان‌گونه که از شکل بالا مشخص است، در $$x=-1$$، تابع نزولی است. این نزولی بودن تا تقریباً $$x=1.2$$ ادامه می‌یابد. پس از آن نیز تابع تا نقطه مورد نظر $$x=2$$ صعودی است.

تذکر: توابع صعودی و نزولی را توابع «یکنوا» (Monotonic) و توابع اکیداً صعودی و اکیداً نزولی را توابع «اکیداً یکنوا» می‌گویند.

تعیین صعودی یا نزولی بودن با استفاده از مشتق

اما اگر بخواهیم بدون استفاده از شکل تابع، درباره صعودی یا نزولی بودن یا نبودن آن بحث کنیم، باید چه‌کار کنیم؟ به تعاریفی که بیان کردیم باز می‌گردیم. برای تابع اکیداً صعودی گفتیم که باید شرط زیر برقرار باشد:

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

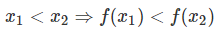
با یک جابه‌جایی جبری، می‌توان نوشت:

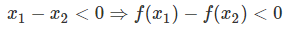
چگونه می‌توانیم رابطه‌ای ریاضی از این تعریف استخراج کنیم؟ بیایید نسبت زیر را بنویسیم:

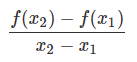
اگر بخواهیم شرط اکیداً صعودی بودن تابع برقرار باشد، حاصل کسر بالا باید مثبت شود، چون صورت و مخرج هر دو مثبت هستند (به جابه‌جایی اندیس‌ها دقت کنید). اما معادله بالا شما را یاد چه چیزی در ریاضیات می‌اندازد؟‌ بله، درست است؛ اگر $$x_1$$ و $$x_2$$ بسیار نزدیک به هم باشند، عبارت کسری بالا تعریف مشتق تابع است. نزدیک بودن $$x_1$$ و $$x_2$$ تناقضی با تعریف صعودی و نزولی بودن توابع ندارد و بنابراین با استفاده از مشتق می‌توان صعودی یا نزولی بودن توابع را در نقاط مورد نظر تحقیق کرد.

قضیه: فرض کنید f یک تابع مشتق‌پذیر در بازه $$(a, b)$$ باشد، بنابراین:

1. اگر برای xهای بازه $$(a, b)$$، داشته باشیم: $$f'(x)<0$$،  آن‌گاه f در آن بازه اکیداً نزولی است.
2. اگر برای xهای بازه $$(a, b)$$، داشته باشیم: $$f'(x)>0$$،  آن‌گاه f در آن بازه اکیداً صعودی است.
3. اگر برای xهای بازه $$(a, b)$$، داشته باشیم: $$f'(x)=0$$،  آن‌گاه f در آن بازه ثابت است.
4. اگر برای xهای بازه $$(a, b)$$، داشته باشیم: $$f'(x) \le 0$$،  آن‌گاه f در آن بازه نزولی است.
5. اگر برای xهای بازه $$(a, b)$$، داشته باشیم: $$f'(x) \ge 0$$،  آن‌گاه f در آن بازه صعودی است.

در حقیقت، اگر شیب نقطه‌ای از نمودار مثبت باشد، تابع در آن نقطه صعودی است و اگر منفی باشد، تابع در آن نقطه نزولی است.

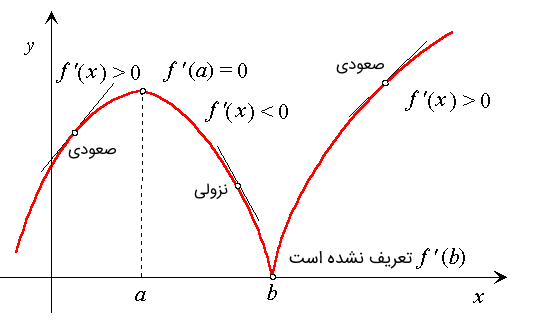
نقاط a و b در نمودار بالا، نقاط بحرانی (Critical point) تابع f نامیده می‌شوند.

تعریف: نقطه c را بحرانی می‌نامیم، اگر $$f'(x)$$ در آن نقطه برابر با صفر یا تعریف نشده باشد.

مثال 2

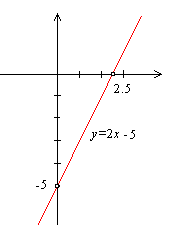
درباره صعودی یا نزولی بودن تابع $$y=2x-5$$ در بازه $$(-\infty, \infty)$$ بحث کنید.

حل: مشتق تابع، $$y'=2$$ است که در کل بازه $$(-\infty, \infty)$$ عددی مثبت است. بنابراین، تابع مذکور همواره صعودی است.

مثال 3

درباره صعودی یا نزولی بودن تابع $$y=x^2-1$$ در بازه $$(-\infty,0)$$ و $$(0,\infty)$$ بحث کنید.

حل: مشتق تابع به‌صورت $$y'=2x$$ است که در بازه $$(-\infty, 0)$$ منفی و در بازه $$(0, \infty)$$ مثبت است. بنابراین، تابع در بازه نخست، اکیداً نزولی و در بازه دوم اکیداً صعودی است.

مثال 4

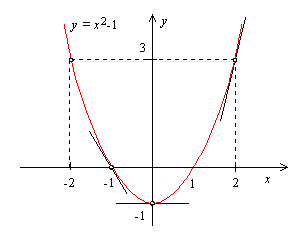
درباره صعودی یا نزولی بودن تابع زیر بحث کنید:

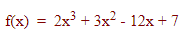
حل: ابتدا، مشتق تابع را می‌گیریم:

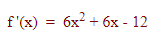
برای تعیین بازه‌های مثبت یا منفی بودن مشتق، باید ریشه‌های آن را پیدا کنیم. با فاکتورگیری از معادله مشتق، داریم:

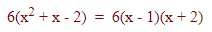
ریشه‌های این معادله، $$x=1$$ و $$x=-2$$ است. بنابراین، تغییر علامت در این دو ریشه رخ می‌دهد. اکنون، برای تعیین علامت، چند عدد را آزمایش می‌کنیم:

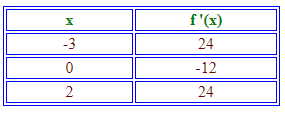
می‌بینیم که مشتق در خارج از بازه $$[-2,1]$$ مثبت و درون آن منفی است. می‌توان نتیجه گرفت که f در خارج از بازه مذکور اکیداً صعودی و در داخل آن، اکیداً نزولی است. شکل تابع به‌صورت زیر است:

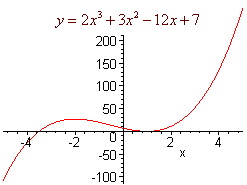
مثال 5

وزن (برحسب پوند) یک نوزاد را در سه ماه اول زندگی می‌توان با رابطه زیر مدل کرد:

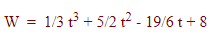
که در آن، t برحسب ماه است. تعیین کنید چه زمانی وزن نوزاد کاهش و چه زمانی افزایش می‌یابد.

حل: برای پاسخ به پرسش مطرح شده، باید تعیین کنیم تابع چه زمانی صعودی و چه زمانی نزولی است. مشتق تابع به‌صورت زیر است:

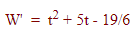
ریشه‌های معادله فوق 0.56 و $$-5.56$$ هستند. از آن‌جایی که فقط سه ماه اول، مورد نظر است، فقط ریشه 0.56 را بررسی می‌کنیم. اکنون جدول تعیین علامت را تشکیل می‌دهیم:

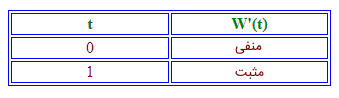
بنابراین، تابع برای tهای بزرگتر از 0.56 صعودی و برای tهای کوچکتر از آن، نزولی است. می‌توان نتیجه گرفت که نوزاد در 0.56 ماه اول زندگی، وزن از دست می‌دهد، سپس وزن او تا ماه سوم افزایش می‌یابد.

مثال 6

گاهی می‌توان بازه‌هایی را که  تابع در آن صعودی یا نزولی است به‌راحتی با فلش‌هایی مشخص کرد. برای مثال، صعودی یا نزوی بودن تابع زیر را مشخص می‌کنیم.

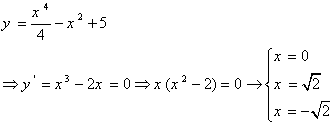
جدول تعیین علامت این تابع، به‌شکل زیر است که نزولی و صعودی بودن بازه‌ها نیز در آن نشان داده شده است:

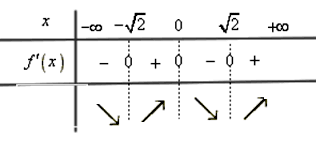
نکته: جمع دو تابع اکیداً صعودی، اکیداً صعودی است و جمع دو تابع اکیداً نزولی، اکیداً نزولی است. اگر f و g هر دو اکیداً صعودی یا هر دو اکیداً نزولی باشند، $$f(g(x))$$ و $$g(f(x))$$ اکیداً صعودی خواهند بود، در حالی که اگر یکی اکیداً صعودی و دیگری اکیداً نزولی باشد، $$f(g(x))$$ اکیداً نزولی خواهد شد.