مرجع تابع لگاریتمی – به زبان ساده

در این آموزش قصد داریم در خصوص تابع لگاریتمی و خصوصیات آن به بحث بپردازیم.

تابع زیر، یک تابع لگاریتمی است:

f(x) = log_a(x)

a هر مقداری بزرگتر از " 0 " و غیر از 1 است.

خصوصیات تابع به مقدار "a" وابسته است

• اگر a = 1 باشد، نمودار تابع تعریف نشده است.
• غیر از مورد بالا، دو حالت امکان پذیر است.

در کل

• نمودار این تابع همواره در ناحیه مثبت محور y است (و هیچوقت آن را قطع نمی کند)
• این تابع همواره در x = 1 محور x ها را قطع می کند... به عبارت دیگر، از نقطه (1,0) عبور می کند.
• در نقطه x = a، تابع برابر با 1 است... به عبارت دیگر، از نقطه (a,1) عبور می کند.
• این تابع، یک تابع یک به یک (Injective) است.
• دامنه این تابع، اعداد حقیقی بزرگتر از 0 است: (∞+ , 0)
• برد این تابع نیز برابر با کل اعداد حقیقی است.

معکوس

تابع لگاریتمی (log_ax) در واقع معکوس تابع نمایی (a^x) است.

پس تابع لگاریتمی می تواند بوسیله تابع نمایی "بازگردانده" شود.

فیلم آموزش حسابان ۱ – پایه یازدهم – حل تمرین در فرادرس

کلیک کنید

تابع لگاریتم طبیعی

تابع زیر، تابع لگاریتم "طبیعی" است.

f(x) = log_e(x)

که e برابر عدد اویلر است و مقدار آن تقریبا برابر است با:

2.718281828459...

اما تابع لگاریتم طبیعی بیشتر به شکل زیر نوشته می شود:

f(x) = ln(x)

ln به معنای لگاریتم طبیعی (Logarithm, Natural) است.

پس هنگامی که ln را دیدید، به یاد بیاورید که همان تابع لگاریتمی با پایه e است:

log_e(x)

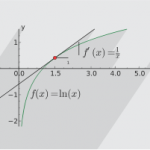
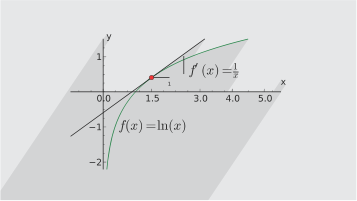
f(x) = ln(x) نمودار

در نقطه (e,1) شیب خط برابر 1 تقسیم بر e است و خط مماس بر منحنی است.