ماکزیمم و مینیمم تابع — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

در مطالب گذشته فرادرس مبحث مشتق را معرفی کردیم. یکی از کاربردهای این ابزار یافتن بیشترین و کم‌ترین مقدار توابع است. بنابراین این سوال را می‌توان مطرح کرد که بیشترین (ماکزیمم) و کم‌ترین (مینیمم) مقدار یک تابع در بازه‌ای مشخص چقدر است؟

چگونه ماکزیمم و مینیمم نسبی یک تابع را بیابیم؟

ماکزیمم نسبی یک تابع در حقیقت مختصاتی است که در آن، تابع نسبت به نقاط اطراف خود به بیشترین مقدارش رسیده. هم‌چنین مینیمم نسبی تابع، نقطه‌ای است که در آن تابع دارای کمترین مقدار، نسبت به نقاط نزدیک خود باشد.

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

در شکل زیر این نقاط نشان داده شده‌اند. در حالت کلی به نقطه‌ای که ماکزیمم یا مینیمم باشد، اکسترمم نیز گفته می‌شود.

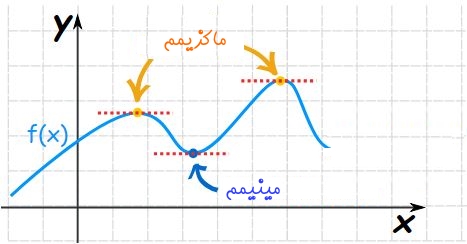
در تابعی که به صورتی یکنواخت تغییر می‌کند، مقادیر ماکزیمم و مینیمم آن، نقاطی هستند که شیب تابع مفروض در آن‌ها برابر با صفر باشد. از آنجایی که شیب یک تابع، برابر با مشتق آن است، بنابراین می‌توان گفت:

ماکزیمم و مینیمم نسبی یک تابع، نقطه‌ای است که مشتق تابع در آن نقطه برابر با صفر باشد. جهت درک بهتر به مثال زیر توجه کنید.

مثال ۱

مطابق با شکل زیر یک توپ با زاویه‌ای نسبت به افق به سمت بالا پرتاب می‌شود. با توجه به ابزار فیزیکی موجود، ارتفاع توپ در هر لحظه را می‌توان مطابق با رابطه زیر بدست آورد.

با این فرضیات، به نظر شما توپ تا چه ارتفاعی بالا می‌رود؟

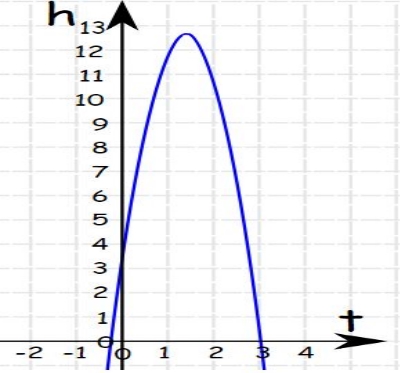
بیشترین ارتفاع در این مسئله برابر با ماکزیمم مقدار تابع h است. جهت بدست آوردن ماکزیمم تابع، در ابتدا مشتق h نسبت به t را می‌گیریم. این مشتق نسبت به زمان برابر است با:

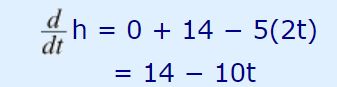
با صفر قرار دادن آن و بدست آوردن t، زمانی که در آن ارتفاع به بیشترین مقدار خود رسیده، بدست می‌آید. با صفر قرار دادن مشتق h نسبت به زمان داریم:

در نتیجه شیب تابع h در لحظه t=1.4 ثانیه برابر با صفر است. ارتفاع متناظر با این زمان نیز با جایگذاری ۱.۴ در رابطه ۱ بدست می‌آید. در نتیجه (h(1.4 برابر است با:

بنابراین بیشترین ارتفاع توپ برابر با ۱۲.۸ متر است که در زمان t=۱.۴ ثانیه رخ می‌دهد.

ماکزیمم یا مینیمم؟

در مثال ۱ از روی نمودار متوجه شدیم که نقطه بدست آمده، ماکزیمم است؛ اما بایستی توجه داشته باشید که شیب نمودار در نقطه مینیمم نیز برابر با صفر است.

فیلم آموزش ریاضی و آمار ۳ – پایه دوازدهم علوم انسانی در فرادرس

کلیک کنید

جهت مشخص کردن این‌که یک نقطه ماکزیمم یا مینیمم است:

• مشتق دوم تابع را در نقطه مفروض بدست آورید.
• اگر مشتق دوم بدست آمده مثبت بود، نقطه مفروض، مینیمم تابع است.
• اگر مشتق دوم منفی بود، نقطه بدست آمده ماکزیمم است.

برای نمونه مشتق دوم تابع h در مثال ۱ برابر است با:

h'' = -10

در نتیجه مشتق دوم تابع h همواره منفی است. در نتیجه این مقدار در زمان t=1.4 نیز کمتر از صفر است؛ بنابراین نقطه مفروض ماکزیمم h محسوب می‌شود.

مثال ۲

ماکزیمم و مینیمم تابع زیر را بیابید.

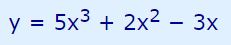
مشتق (یا همان شیب) تابع y برابر است با:

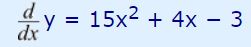
رابطه بالا از مرتبه دوم است بنابراین دارای ۲ ریشه خواهد بود. در نتیجه با حل آن، ریشه‌های x برابر هستند با:

به نظر شما آیا این دو نقطه ماکزیمم، مینیمم و یا هردو هستند؟ برای پاسخ به این سوال در ابتدا مشتق دوم تابع y را مطابق با رابطه زیر می‌یابیم.

مقدار این تابع در دو نقطه بدست آمده برابر است با:

شکل زیر تابع y را نشان می‌دهد. همان‌طور که در آن می‌بینید در $$x= \large \frac{1}{3}$$ مقدار تابع مینیمم و در  نقطه $$x= \large - \frac{3}{5}$$، مقدار تابع ماکزیمم است.

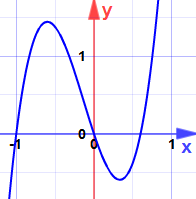
توجه داشته باشید که این روش تنها در حالتی استفاده می‌شود که تابع در نقطه مورد بررسی، مشتق پذیر باشد. برای نمونه تابع |y=|x را در نظر بگیرید. همان‌طور که در شکل زیر نیز نشان داده شده، این تابع در x=0 مشتق‌پذیر نیست، در نتیجه نمی‌توان با استفاده از روش بیان شده در این مطلب ماکزیمم و یا مینیمم بودن نقطه x=0 را بررسی کرد.

در این آموزش مثال‌های بسیاری در مورد ماکزیمم و مینیمم تابع، به صورت ویدئویی ارائه شده که جهت تسلط بیشتر شما به این موضوع، می‌تواند کمک کننده باشد. در مطالب آینده در مورد ارتباط بین نقطه عطف و مشتق دوم تابع صحبت خواهیم کرد.