قدر مطلق – به زبان ساده

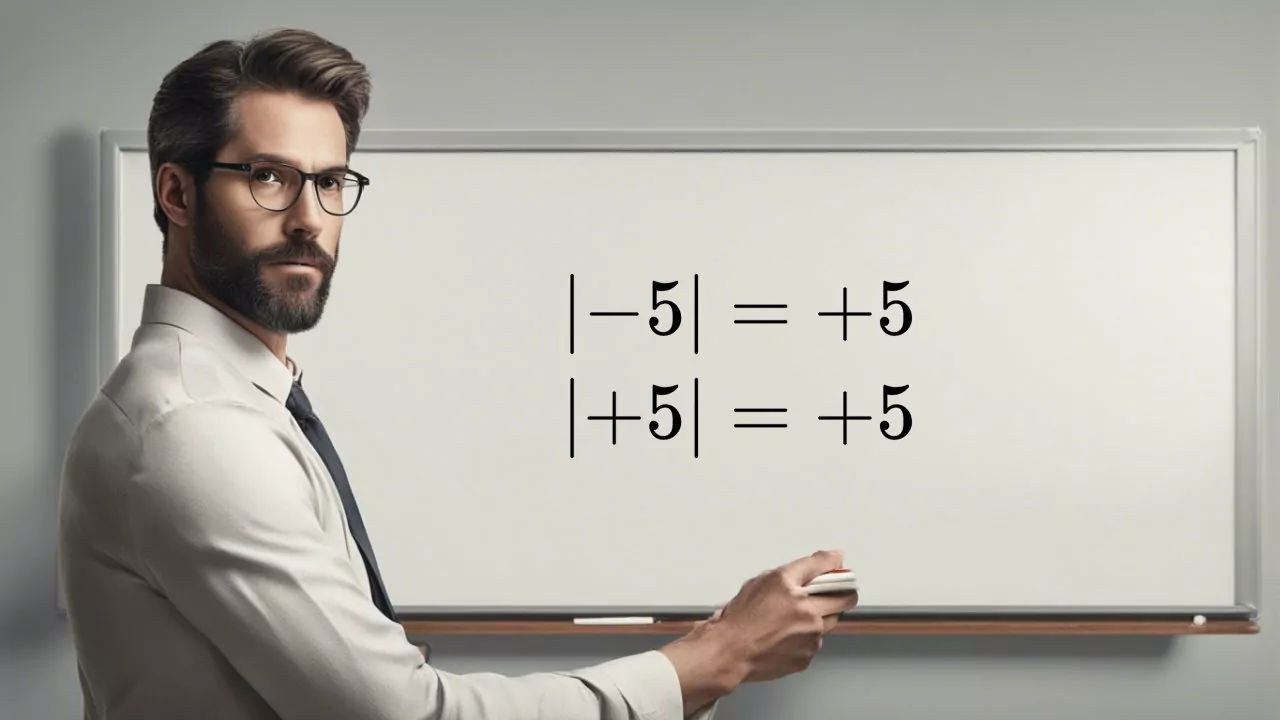
در این مطلب از مجله فرادرس در مورد قدر مطلق صحبت می‌کنیم. یکی از مفاهیم بسیار مهم و ساده در ریاضیات، مفهوم قدر مطلق است. این مفهوم، فاصله یک عدد با مبدا (صفر) را نشان می‌دهد. این موضوع در شکل زیر نشان داده شده است.

همانطور که در شکل بالا نشان داده شده، عدد 6 به اندازه 6 واحد از صفر فاصله دارد و فاصله عدد 6- از صفر نیز برابر با 6 واحد است. بنابراین می‌توان بیان کرد که قدر مطلق عدد ۶ برابر با ۶ و قدر مطلق 6- نیز برابر با 6 است.

نماد قدر مطلق

برای نمایش قدر مطلق، علامت «|» را در هر دو سمت عدد قرار می‌دهیم.

شیوه نمایش قدر مطلق در دو مثال زیر نشان داده شده است.

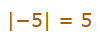
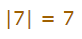
این دو مثال نشان می‌دهند که قدر مطلق عدد 5- برابر با 5 و قدر مطلق عدد 7 برابر با خود 7 است.

تعریف ریاضی قدر مطلق

به صورت ریاضی می‌توان نشان داد که قدر مطلق، یک تابع ریاضی است که به شکل زیر نمایش داده می‌شود.

رابطه بالا نشان می‌دهد که قدر مطلق عدد x زمانی که مقدار x بزرگتر از صفر باشد، با خود x برابر است و زمانی که عدد x مقداری کوچکتر از صفر داشته باشد، قدر مطلق آن برابر با x- است. نکته مهم دیگر این است که قدر مطلق عدد صفر، دقیقا برابر با صفر است.

بنابراین، اگر عددی که قرار است قدر مطلق آن را محاسبه کنیم، مثبت باشد، قدر مطلق آن با خودش برابر است و زمانی که این عدد، منفی باشد ما آن را به استفاده از عبارت x- تبدیل به یک عدد مثبت می‌کنیم.

در واقع خروجی تابع قدر مطلق، همواره یک عبارت مثبت است. مثال زیر شیوه محاسبه قدر مطلق را به خوبی مورد بررسی قرار می‌دهد.

مثال

قدر مطلق عدد 17- را محاسبه کنید.

برای محاسبه قدر مطلق این عدد، ابتدا به این سوال پاسخ بدهید که این عدد، مقداری مثبت و یا منفی دارد؟ بنابراین از آنجایی که عدد داده شده مقداری منفی دارد، قدر مطلق‌ آن با منفی آن عدد، یعنی x- برابر است.

توضیحات بالا، در رابطه زیر به خوبی نشان داده شده‌اند.

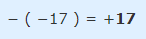
برای محاسبه عبارت بالا از این نکته استفاده شده که منفی یک عبارت منفی برابر با یک مقدار مثبت می‌شود. (منفیِ منفی = مثبت)

خواص قدر مطلق

در این قسمت، برخی از خواص بسیار مهم قدر مطلق بیان شده است.

یادگیری مفهومی و گام به گام این مفاهیم شما را برای حل مسائل پیچیده ریاضی آماده می‌کند. بنابراین توصیه ما این است که این روابط و توضیحات مربوط به آن‌ها را با دقت مطالعه کنید و از آن‌ها یادداشت برداید.

خاصیت 1

مقدار خروجی تابع قدر مطلق همواره بزرگتر و یا مساوی با صفر است. این موضوع با استفاده از رابطه زیر نشان داده می‌شود.

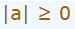
این رابطه یکی از مهم‌ترین مفاهیم قدر مطلق است.

خاصیت 2

توان دوم یک عدد مانند a، آن عدد را تبدیل به یک عدد مثبت یا صفر می‌کند (این موضوع زمانی صادق است که عدد a، یک عدد حقیقی باشد). در صورتی که از این مقدار (توان دوم a)، جذر بگیریم، عمل توان دو از بین می‌رود ولی عدد a به یک عدد مثبت یا صفر تبدیل می‌شود (حتی اگر عدد a در ابتدا یک عدد منفی بوده باشد).

این خاصیت، با استفاده از رابطه زیر نشان داده شده است.

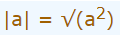
خاصیت 3

سومین خاصیتی که در مفهوم قدر مطلق وجود دارد این است که حاصل ضرب قدر مطلق دو عبارت a و b (سمت راست رابطه زیر)، با قدر مطلق حاصل ضرب دو عبارت a و b (سمت چپ رابطه زیر) با یکدیگر یکسان هستند.

این خاصیت با استفاده از عبارت زیر بیان شده است.

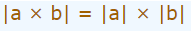
خاصیت 4

فرض کنید که بعد از حل یک معادله ریاضی، به عبارتی مشابه با رابطه زیر رسیدید:

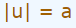
در این صورت عبارت مجهول u، دو مقدار مختلف را می‌تواند اختیار کند. یکی از این دو مقدار برابر با a و دیگری برابر با a- است. این موضوع در رابطه زیر نشان داده شده است.

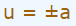
این خاصیت یکی از مهم‌ترین نکاتی است که در مسائل قدر مطلق باید به آن توجه کنید. در واقع حاصل مقدار مجهول u دو عدد مختلف را در بر می‌گیرد.

در صورتی که این خاصیت را در نظر نگیرید و مقدار u را تنها برابر با a قرار دهید، یکی از پاسخ‌های مسئله را از دست خواهید داد. اهمیت این خاصیت در مسائل قدر مطلق با استفاده از مثال زیر بیان شده است.

مثال

معادله زیر که به صورت قدر مطلق داده شده را در نظر بگیرید.

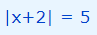
مقدار x را در معادله بالا بیابید.

همانطور که در خاصیت بالا (خاصیت 4) نشان داده شد، در چنین شرایطی، مقدار مجهول مسئله، دو مقدار مختلف را می‌تواند اختیار کند. بنابراین مطابق با خاصیت 4، عبارت داخل قدر مطلق به شکل زیر بیان می‌شود.

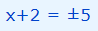
در صورتی که عبارت بالا برابر با 5 باشد، مقدار x به شکل زیر محاسبه می‌شود.

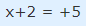
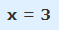
در صورتی که عبارت x+2 برابر با 5- باشد، مقدار x به شکل زیر محاسبه می‌شود.

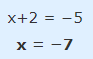
بنابراین همانطور که مشاهده شد، مقدار مجهول در این عبارت انتگرالی شامل دو مقدار 3 و 7- است.

نمودار قدر مطلق

در این قسمت ابتدا نمودار تابع قدر مطلق x را رسم می‌کنیم.

سپس با استفاده از مفاهیم رسم نمودار، نمودار یک تابع نسبتا پیچیده را مورد بررسی قرار می‌دهیم. توجه شود که نمودار تابع $$y = | x |$$ به شکل زیر رسم می‌شود.

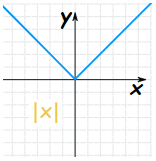
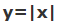
حال فرض کنید که می‌خواهیم مثال بخش قبل را با استفاده از رسم نمودار حل کنیم. بنابراین تابع مورد نظر را به شکل زیر بازنویسی می‌کنیم.

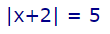
برای محاسبه جواب‌های این تابع، ابتدا تمام عبارت‌ها را به یک سمت منتقل می‌کنیم.

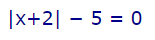
این رابطه را می‌توان به فرم تابع زیر نمایش داد که در آن y برابر با صفر است.

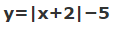
بنابراین برای یافتن پاسخ‌های این مسئله، کافی است که نمودار تابع فوق را رسم کنیم و سپس محل برخورد این نمودار با محور xها (y=0) را علامت بزنیم. این محل نشان‌دهنده پاسخ مسئله است. برای رسم این تابع، ابتدا با نمودار قدر مطلق x شروع می‌کنیم و آن را به شکل زیر رسم می‌کنیم.

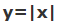
در ادامه با استفاده از نمودار قدر مطلق x، نمودار |x+2| را به شکل زیر محاسبه می‌کنیم.

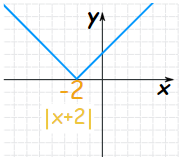
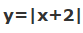
مشاهده می‌شود که برای رسم نمودار قدر مطلق به فرم |x+2|، نمودار قدر مطلق |x| را به اندازه ریشه عبارت داخل قدر مطلق یعنی حاصل x+2=0، به صورت افقی جابه‌جا می‌کنیم.

در این مثال برای رسم نمودار |x+2|، با توجه به اینکه ریشه عبارت داخل قدر مطلق برابر با 2- است، نمودار قدر مطلق |x| را به اندازه 2- واحد جابه‌جا می‌کنیم. این موضوع در شکل بالا نشان داده شده است.

حال با استفاده از نمودار |x+2|، نمودار تابع 5-|x+2| را به شکل زیر رسم می‌کنیم.

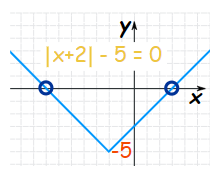
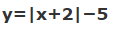
برای رسم این تابع، نمودار |x+2| را به اندازه 5 واحد در جهت عمودی به سمت پایین حرکت دادیم.

همانطور که نشان دادیم، محل برخورد نموداری که در شکل بالا رسم شده، با محور xها، پاسخ مسئله را بیان می‌کند. این مقادیر برابر با 7- و 3+ هستند که دقیقا همان مقادیری را نشان می‌دهند که در مثال قسمت قبل محاسبه شدند.

قدر مطلق و نامساوی‌ها

استفاده از نامساوی‌ها در توابع قدر مطلق نیاز به دقت بسیار زیادی دارد.

در ریاضیات 4 نامساوی مهم به شکل زیر موجود هستند.

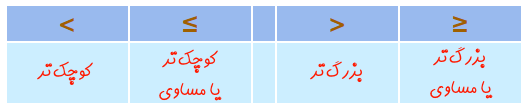
نامساوی کوچک‌تر و کوچک‌تر مساوی

نامساوی‌ کوچک‌تر و کوچک‌تر مساوی، به ترتیب با استفاده از نمادهای > , $$\leq$$ نمایش داده می‌شوند. زمانی که این دو نامساوی در معادلات قدر مطلق دیده می‌شوند، پاسخ نهایی در محدوده‌ای درون یک بازه قرار خواهد داشت. برای نشان دادن این مفهوم چند مثال آورده شده است.

مثال 1

مقایر x در رابطه زیر درون چه محدوده‌ای قرار می‌گیرد و این رابطه چه مفهوم ریاضی را منتقل می‌کند.

این عبارت بیان می‌کند که x در محدوده‌ای قرار دارد که فاصله آن تا مبدا (x=0) برابر با ۳ است. این موضوع در شکل زیر به تصویر کشیده شده است.

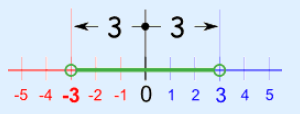
همانطور که مشاهده می‌شود محدوده قرار گرفتن x، فاصله بین 3- و 3+ (خود ۳ و 3- بخشی از بازه نیستند) است. شکل بالا را می‌توانیم با استفاده از نامساوی زیر نمایش دهیم.

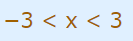
مثال 2

مثال بالا را در حالتی پاسخ دهید که نامساوی موجود در آن به صورت زیر تعریف شده باشد.

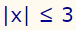
پاسخ این نامساوی تمام نقاط در بازه 3- تا 3 است و خود 3 و 3- را نیز شامل می‌شود. این موضوع با استفاده از نامساوی زیر نشان داده شده است.

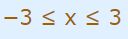
در ادامه یک مثال نسبتا سخت‌تر را درمورد نامساوی کچک‌تر مساوی مورد بررسی قرار می‌دهیم.

مثال 3

x در نامساوی زیر در چه محدوده‌ای قرار می‌گیرد.

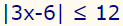
همانطور که توضیح داده شد، در شرایط بالا، عبارت داخل انتگرال در محدوده بین 12- تا 12 قرار می‌گیرد. بنابراین رابطه بالا به شکل زیر بازنویسی می‌شود.

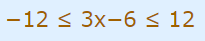
با افزودن عدد ۶ به طرفین این نامساوی، عبارت فوق به شکل زیر در می‌آید.

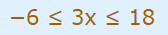
حال برای یافتن محدوده x، طرفین این نامساوی را در $$1 \over 3$$ ضرب می‌کنیم. بنابراین محدوده متغیر x به شکل رابطه زیر در می‌آید.

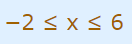
نامساوی بزرگ‌تر و بزرگ‌تر مساوی

مهم‌ترین و اصلی‌ترین تفاوت بین این بخش و نامساوی بخش قبل این است که در بخش قبل جواب ما در یک بازه قرار داشت ولی پاسخ مسئله در این بخش در دو بازه متفاوت قرار دارد. در ادامه، این موضوع با استفاده از چند مثال به صورت دقیق بررسی می‌شود.

مثال 1

محدوده قرار گرفتن متغیر x در نامساوی زیر را محاسبه کنید.

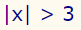
همانطور که در تعریف قدر مطلق بیان شد، زمانی که قدر مطلق متغیر x بزرگتر از 3 باشد، منظور این است که x اعدادی را شامل می‌شود که فاصله آن‌ها از مبدا (x=0) بیشتر از ۳ باشد. این موضوع در شکل زیر به تصویر کشیده شده است.

در واقع این شکل نشان می‌دهد که x در بازه کوچکتر از 3- و بزرگتر از 3 قرار دارد. این موضوع در نامساوی‌های زیر نشان داده شده است.

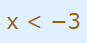
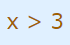
این دو نامساوی را با استفاده از اجتماع دو بازه به شکل زیر هم می‌توانیم نمایش دهیم.

نکته بسیار مهم:

عبارت فوق را ابدا به شکل رابطه زیر ننویسید.

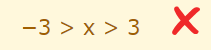
هیچوقت x نمی‌تواند بزرگ‌تر از 3 «و» کوچک‌تر از 3- باشد. در واقع تنها به کمک رابطه زیر می‌توانیم این نامساوی را نمایش دهیم.

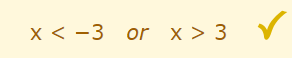
این دو نامساوی نشان می‌دهند که x بزرگ‌تر از 3 «یا» کوچک‌تر از 3- است. در ریاضیات دو واژه «و» و «یا» تفاوت‌های عظیمی را ایجاد می‌کنند.

مثال 2

مثال فوق را برای حالتی که علامت نامساوی به شکل بزرگ‌تر مساوی باشد، تکرار کنید. در واقع محدوده x در نامساوی زیر را بیاید.

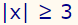
پاسخ این مثال، همان پاسخ مثال قبل است با این تفاوت که علامت مساوی به نامساوی‌ها اضافه می‌شود. بنابراین x در محدوده زیر قرار می‌گیرد.

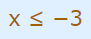
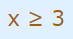
این دو نامساوی را با استفاده از اجتماع دو بازه به شکل زیر هم می‌توانیم نمایش دهیم.

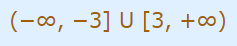
این مطلب ابتدا به صورت دقیق مفهوم قدر مطلق را مورد بررسی قرار داد. سپس نماد قدر مطلق و تعریف ریاضی آن مورد بررسی قرار گرفت. در ادامه خواص قدر مطلق به صورت دقیق ارزیابی شدند و در نهایت شیوه حل نامعادلات و نامساوی‌هایی که شامل قدر مطلق هستند مورد بررسی قرار گرفتند.