فرمول های ترمودینامیک – خلاصه شده + اثبات و مثال

ترمودینامیک علمی است که رابطه بین گرما، کار، دما و انرژی را بیان میکند و انتقال انرژی از نقطهای به نقطه دیگر و از شکلی به شکل دیگر را توضیح میدهد. از خواص مورد بررسی در این علم میتوان به دما، فشار، آنتالپی و آنتروپی اشاره کرد. این پارامترها تحت قوانین صفرم، اول، دوم و سوم ترمودینامیک مورد بحث و بررسی قرار میگیرند. در مطالب قبلی در مورد مفهوم ترمودینامیک و قانونهای آن صحبت کردیم. در این مطلب از مجله فرادرس، فرمول های ترمودینامیک را همراه با اثبات آنها توضیح میدهیم.
فرمول های ترمودینامیک چیست ؟
فرمول های ترمودینامیک، قوانین و رابطههای حاکم بر این علم را بیان میکنند. ترمودینامیک به بخشهای مختلفی تقسیم میشود که هر بخش فرمولهای مربوط به خود دارد. گرچه، فرمولهای بخشهای مختلف را میتوان به یکدیگر مربوط ساخت و رابطههای جدیدی را بهدست آورد. در این مطلب، فرمول های ترمودینامیک در بخشهای مختلف را بهدست میآوریم و به زبان ساده آنها را اثبات میکنیم.
- فرمول های ترمودینامیک برای گاز کامل
- فرمول های ترمودینامیک در قانون اول
- فرمول های ترمودینامیک در قانون دوم
- فرمول های ترمودینامیک در قانون سوم
- فرمول های ترمودینامیک برای گاز واقعی
- فرمول های ترمودینامیک برای علم مواد
فرمول های ترمودینامیک برای گاز کامل
یکی از مهمترین فرمول های ترمودینامیک که در ابتدای مطالعه این مبحث با آن مواجه میشویم، فرمول گاز کامل است:
$$PV = n R T$$
در رابطه فوق:
- P فشار گاز است.
- $$V$$ حجم گاز است.
- n تعداد مولها در حجم $$V$$ است.
- R ثابت جهانی گازها و مقدار آن برابر $$0.08206 \ \frac { L . atm } { mol - K }$$ است. به این نکته توجه داشته باشید که هرگاه در یکی از فرمول های ترمودینامیک از این ثابت استفاده شود، واحد حجم باید لیتر و واحد فشار باید اتمسفر باشد.
- T دمای گاز و واحد آن کلوین است.
برای تبدیل دما از سلسیوس به کلوین از رابطه زیر استفاده میکنیم:
$$ T _ K = T _ C + 273$$
به این نکته توجه داشته باشید که مقدار ثابت جهانی گازها ممکن است برابر $$8.3145 \ \frac { I} {mol . K }$$ نیز باشد. در این حالت، واحد فشار برحسب کیلوپاسکال بیان میشود. با استفاده از معادله $$PV = n R T$$ میتوانیم به معادلههای دیگری نیز برسیم. طرفین این رابطه را بر nT تقسیم میکنیم:
$$PV = nR T \\ \frac{PV}{nT} = \frac{nRT}{nT} \\ R = \frac{PV}{nT}$$
فرض کنید گازی از حالت یک با حجم $$V_1$$، فشار $$P_1$$ و دمای $$T_1$$ به حالت دو با حجم $$V_2$$، فشار $$P_2$$ و دمای $$T_2$$ میرود. با توجه به رابطه بالا حالتهای یک و دو را میتوانیم به صورت زیر بنویسیم:
$$1: \enspace R = \frac{P_1 V_ 1}{n_ 1 T _1} \\ 2: \enspace R = \frac{P_2 V_ 2}{n_ 2 T _ 2}$$
از آنجا که R ثابت است، کسرهای $$\frac{P_1 V_ 1}{n_ 1 T _1} $$ و $$\frac{P_2 V_ 2}{n_ 2 T _ 2}$$ با یکدیگر برابر هستند:
$$ \frac{P_1 V_ 1}{n_ 1 T _1} = \frac{P_2 V_ 2}{n_ 2 T _ 2}$$
به تساوی بهدست آمده، قانون ترکیبی گازها گفته میشود.
تا اینجا با اصلیتریم فرمول های ترمودینامیک برای گاز کامل آشنا شدیم.
قانون بویل چیست ؟
قانون بویل رابطه بین فشار و حجم را بیان میکند. بنابراین، تعداد مولها و دما ثابت میمانند.
$$P _ 1 V_ 1 = P_2 V_2$$
نمودار فشار برحسب حجم به شکل نشان داده شده در تصویر زیر است. با توجه به نمودار نشان داده شده، با افزایش حجم، فشار کاهش مییابد. بنابراین، فشار و حجم با یکدیگر رابطه عکس دارند. اگر حجم ظرف حاوی گاز را دو برابر کنیم، فشار آن نصف میشود.
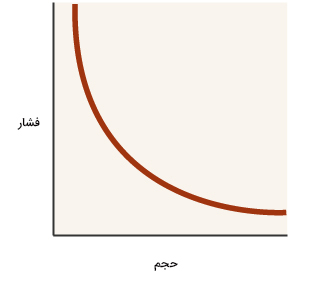
قانون شارل چیست ؟
یکی از مهمترین فرمول های ترمودینامیک، رابطه شارل است. قانون شارل رابطه بین حجم و دما را نشان میدهد. بار دیگر فرمول زیر را در نظر میگیریم:
$$ \frac{P_1 V_ 1}{n_ 1 T _1} = \frac{P_2 V_ 2}{n_ 2 T _ 2}$$
در قانون شارل، فشار و تعداد مولها را ثابت در نظر میگیریم:
$$\frac { V_ 1 } { T _ 1} = \frac { V_2 } { T_ 2 }$$
با توجه به رابطه بالا، اگر دمای گاز افزایش یابد، حجم گاز نیز افزایش خواهد یافت. نمودار حجم برحسب دما در تصویر زیر نشان داده شده است. همانطور که مشاهده میکنیم، حجم برحسب دما به صورت خطی تغییر میکند. به بیان دیگر، رابطه بین دما و حجم خطی است.
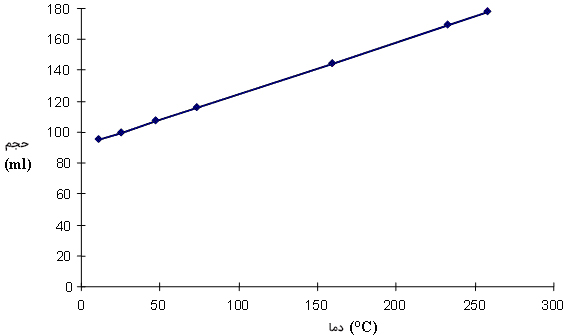
قانون گیلوساک چیست ؟
قانون یا رابطه گیلوساک به عنوان یکی از فرمول های مهم ترمودینامیک، رابطه بین فشار و دما را نشان میدهد. بنابراین، حجم و تعداد مولها ثابت باقی میمانند.
$$\frac { P_ 1 } { T _ 1} = \frac { P_2 } { T_ 2 }$$
اگر دمای گازی را افزایش دهیم، فشار آن کاهش مییابد. نمودار فشار برحسب دما، نموداری خطی است. به عنوان مثال، اگر دما را دو برابر کنیم، فشار گاز نیز دو برابر خواهد شد.
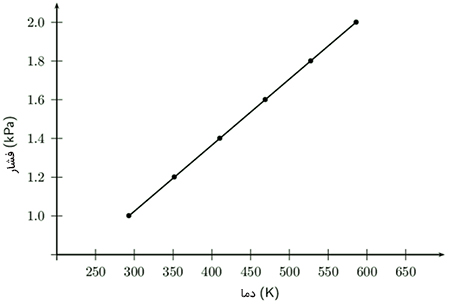
قانون آووگادرو چیست ؟
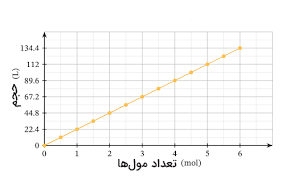
قانون آووگادرو یکی دیگر از فرمول های مهم ترمودینامیک است. این قانون رابطه بین مول و حجم را توصیف میکند. بنابراین، فشار و دما ثابت باقی میمانند.
$$\frac { V_ 1 } {n _ 1} = \frac { V_2 } { n _ 2 }$$
اگر تعداد مولهای داخلی محفظه را افزایش دهیم، حجم نیز افزایش خواهد یافت. نمودار حجم برحسب تعداد مولها در تصویر زیر رسم شده است.
چگالی گاز معادله دیگری است که باید در مورد آن صحبت کنیم. چگالی را به صورت نسبت جرم به حجم تعریف میکنیم. جرم گازها برحسب گرم و حجم آنها برحسب لیتر بیان میشود. بنابراین، به طور معمول، چگالی گازها را برحسب گرم بر لیتر مینویسیم. در حالت کاربردی از چه معادلهای استفاده میشود؟ برای پاسخ به این پرسش از معادله $$PV = n R T$$ شروع میکنیم. نخستین نکتهای که باید به ذهن بسپاریم آن است که تعداد مولهای گاز برابر نسبت جرم به جرم مولی است:
$$n = \frac { m } { M }$$
کسر فوق را در رابطه $$PV = n R T$$ قرار میدهیم:
$$PV = \frac { m } { M } R T$$
در ادامه، طرفین رابطه فوق را در جرم مولی ضرب میکنیم:
$$M \times PV = \frac { m } { M } R T \times M \\ PVM = m RT$$
طرفین رابطه بهدست آمده را بر حجم تقسیم میکنیم:
$$\frac {PV M } { V} = \frac { m R T } { V } \\ PM = \frac { m R T } { V }$$
کسر $$\frac { m R T } { V }$$ در رابطه بالا را به صورت $$\frac { m } { V } RT$$ مینویسیم. نسبت جرم به حجم همان چگالی است:
$$PM = d RT$$
بنابراین، با داشتن جرم مولی، فشار و دمای گاز میتوانیم چگالی آن را بهدست آوریم. رابطه $$PM = d RT$$ را برحسب چگالی مرتب میکنیم:
$$d = \frac { PM } { R T }$$
اگر فشار گاز را افزایش دهیم، چگالی آن چه تغییری میکند؟ از آنجا که فشار و چگالی با یکدیگر رابطه مستقیم دارند، با افزایش فشار، چگالی گاز نیز افزایش مییابد. جرم مولی چه تاثیری روی چگالی گاز دارد؟ جرم مولی نیز همانند فشار در صورت کسر قرار دارد و با چگالی گاز به طور مستقیم تغییر میکند. اگر جرم مولی گاز افزایش یابد، چگالی آن نیز افزایش خواهد یافت. دما، در مخرج کسر قرار دارد، بنابراین با چگالی گاز رابطه معکوس دارد. اگر دمای گاز را افزایش دهیم، چگالی آن کاهش مییابد.
پرسش ۱
اگر دمای گازی افزایش یابد اما حجم آن ثابت بماند، چگالی گاز چگونه تغییر میکند؟
پاسخ
اگر حجم ثابت باقی بماند میتوانیم از قانون گیلوساک استفاده کنیم. با افزایش دما، فشار کاهش مییابد. هرگاه فشار افزایش یابد، چگالی گاز نیز افزایش خواهد یافت. اما در مطالب بالا گفتیم با افزایش دما، چگالی کاهش مییابد. در نتیجه، افزایش فشار اثر کاهش دما را خنثی میکند و چگالی گاز ثابت میماند.
قانون دالتون برای فشار جزیی
قانون دالتون یکی از مهم ترین فرمول های ترمودینامیک در محاسبه فشار جزیی است. بر طبق این قانون، فشار کل گاز برابر مجموع فشارهای جزیی آن است.
$$P _ T = P _ 1 + P _2 + P _ 3 + ...$$
به عنوان مثال، اگر فشار جزیی گازهای نیتروژن، اکسیژن و آرگون به ترتیب برابر ۵۰۰، ۲۰۰ و ۵۰ تور باشد، فشار کل برابر مجموع فشارهای جزیی هر گاز و برابر ۷۵۰ تور است. شاید از خود پرسیده باشید تفاوت فشار کل و فشار جزیی چیست؟ فشار جزیی گاز نیتروژن فشاری است که تنها از مولکولهای گاز نیتروژن ناشی میشود. اما فشار کل، ناشی از تمام مولکولها است.
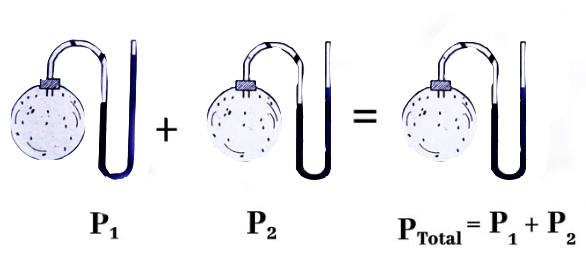
مربع سرعت میانگین مولکول های گاز
معادله دیگری که باید بدانیم، معادله مربوط به میانگین سرعت کل مولکولهای گاز، $$v_{rms}$$، است. این معادله یکی از معادلات مهم در فرمول های ترمودینامیک در فیزیک است. انرژی جنبشی متوسط گاز با استفاده از رابطه زیر بهدست میآید:
$$\overline{KE}_{avg} = \frac { 3 } { 2 } R T$$
انرژی جنبشی هر یک از مولکولهای گاز ممکن است متفاوت باشند، اما انرژی جنبشی میانگین با استفاده از رابطه بالا بهدست میآید. برخی مولکولها در گاز ممکن است سریع و برخی دیگر ممکن است آهسته حرکت کنند. همانطور که در رابطه فوق دیده میشود، میانگین انرژی جنبشی تمام مولکولهای گاز، تنها به دما بستگی دارد. بنابراین، اگر دمای گاز ثابت باشد، میانگین انرژی جنبشی آن نیز ثابت باقی میماند. همچنین، اگر دمای گاز افزایش یابد، میانگین انرژی جنبشی آن نیز افزایش خواهد یافت. در مورد انرژی جنبشی تک مولکول گاز چه چیزی میتوانیم بگوییم؟
از فیزیک پایه میدانیم که انرژی جنبشی مولکولِ تک با استفاده از رابطه $$\frac { 1 } { 2 } m v ^ 2$$ بهدست میآید. بنابراین، انرژی جنبشی هر تک مولکول گاز به جرم آن مولکول و سرعت حرکت آن بستگی دارد. اما انرژی چنبشی متوسط، تنها به دما وابسته است. با ترکیب دو معادله $$\frac { 1 } { 2 } m v ^ 2 , \overline{KE}_{avg} = \frac { 3 } { 2 } R T$$ میتوانیم مربع سرعت متوسط را بهدست آوریم. اما هنگام انجام این کار باید به یکای اندازهگیری توجه داشته باشیم. واحد R برابر $$\frac { J } { mol . K }$$ است. حاصلضرب R در دما، واحد ژول بر مول را به ما میدهد. توجه به این نکته مهم است که مقدار R در انرژی متوسط میانگین برابر ۸/۳۱۴۵ ژول بر مول است.
اما واحد انرژی جنبشی برای هر مولکول گاز، ژول است. از اینرو، یکاهای انرژی جنبشی متوسط و انرژی جنبشی هر مولکول با یکدیگر برابر هستند. برای آنکه یکای انرژی جنبشی هر مولکول گاز برابر یکای انرژی جنبشی متوسط باشد، باید به گونهای واحد مول را به انرژی جنبشی متوسط هر ذره معرفی کنیم. برای انجام این کار، فرمول $$\frac { 1 } { 2 } m v ^ 2$$ را در $$\frac { 1 } { n}$$ ضرب میکنیم:
$$KE = \frac { 1 } { 2 } m v ^ 2 .\times \frac { 1 } { n}$$
در نتیجه داریم:
$$\frac { KE} { mol} = KE_ { avg} \\ \frac { 1 } { n} \times \frac { 1 } {2 } m v ^ 2 = \frac { 3 } { 2 } R T$$
طرفین تساوی فوق را در ۲ ضرب میکنیم:
$$2 \times \frac { 1 } { n} \times \frac { 1 } {2 } m v ^ 2 = \frac { 3 } { 2 } R T \times 2 \\ \frac { m } { n} v ^ 2 = 3 R T$$
در مطالب بالا دیدیم تعداد مولها، برابر $$\frac { m } { M}$$ است. بنابراین، جرم مولی با استفاده از رابطه بالا بهدست میآید:
$$M = \frac { m } { n }$$
در نتیجه، در رابطه $$\frac { m } { n} v ^ 2 = 3 R T$$ به جای کسر $$\frac { m } { n}$$ جرم مولی، M، را قرار میدهیم:
$$M v ^ 2 = 3 RT$$
رابطه فوق را برحسب $$v ^ 2$$ مرتب میکنیم:
$$v ^ 2 = \frac { 3 R T } { M }$$
از طرفین رابطه بهدست آمده جذر میگیریم:
$$v = \sqrt{\frac{ 3 R T }{M}}$$
مقدار R در رابطه فوق برابر ۸/۳۱۴۵ است. همچنین، واحد اندازهگیری جرم مولی به جای گرم بر مول باید کیلوگرم بر مول باشد. افزایش دمای گاز چه تاثیری روی سرعت حرکت مولکولهای گاز دارد؟ همانطور که در رابطه سرعت میانگین دیده میشود، دما در صورت کسر قرار دارد، بنابراین مولکولهای گاز با سرعت بیشتری حرکت میکنند. از اینرو، مولکولهای گاز در دمای بالا با سرعت زیادی حرکت میکنند. همچنین، با افزایش جرم مولی گاز، مولکولهای با سرعت کمتری حرکت خواهند کرد. این نتیجه دور از انتظار نیست. زیرا مولکولهای سنگین گاز آهستهتر از مولکولهای سبک گاز حرکت میکنند.
مثال محاسبه تعداد مول ها با استفاده از فرمول گاز ایده ال
ورزشکاری نفس عمیق میکشد و ۱/۸۵ لیتر هوای ۲۱ درجه سلسیوس با فشار ۷۵۴ میلیمتر جیوه را وارد ریههای خود میکند. تعداد مولِ هوای تنفس ورزشکار چه مقدار است؟ تعداد مولکولها را بهدست آورید.
برای حل این مثال از اطلاعات داده شده در ادامه استفاده نمایید.
$$R = 8.314 \ J \ mol ^ { -1 } \ K ^ { -1 } \\ = 0.08206 \ L \ atm \ mol ^ { -1 } \ K ^ { -1 } \\ = 62.36 \ L \ Torr \ mol ^ { -1 } \ K ^ { -1 } \\ 1 \ atm = 760 \ mm \ Hg = 760 \ Torr$$
پاسخ
در این مثال، با استفاده از فشار، دما و حجم داده شده باید تعداد مولها را بهدست آوریم. نخستین رابطهای که برای حل این مثال به ذهن میرسد رابطه گاز کامل است:
$$PV = n RT$$
n را باید بهدست آوریم. برای محاسبه n، رابطه فوق را برحسب n مینویسیم:
$$n = \frac { PV} { RT}$$
از آنجا که هر ۷۶۰ میلیمتر جیوه برابر ۷۶۰ تور است، هر یک میلیمتر جیوه نیز برابر یک تور خواهد بود. بنابراین، فشار ۷۵۴ میلیمتر جیوه برابر ۷۵۴ تور است. همچنین، حجم برحسب لیتر داده شده است، در نتیجه باید از مقدارهای ثابت جهانی گاز داده شده باید مقداری را انتخاب کنیم که برحسب لیتر و تور بیان شده باشد.
$$n = \frac { 754 \ torr \times 1.85 \ L } { 294 \ K \times 62.36 \ \frac { L \ torr } { mol \ K }} \\ n \approx 0.0761$$
در ادامه، تعداد مولکولها را بهدست میآوریم. برای انجام این کار باید تعداد مولها را در عدد آووگادرو ضرب کنیم:
$$0.0761 \times 6.022 \times 10 ^ { 23} = 4.58 \times 10 ^ { 22} \ molecules$$
مثال محاسبه تغییرات حجم با استفاده از فرمول گاز ایده ال
بالونی با مقدار $$1.85 \times 10 ^ 3$$ لیتر هلیوم در دمای ۲۳ درجه سلسیوس و فشار ۷۶۵ تور به هوا فرستاده میشود. بالون قبل از ترکیدن به مدت دو ساعت پرواز میکند و تا ارتفاع ۳۲ کیلومتر بالا میرود. اگر دما در این ارتفاع برابر ۴۴- درجه سلسیوس و فشار برابر ۶/۵۱ تور باشد، حجم بالون قبل از ترکیدن چه مقدار است؟

پاسخ
برای حل این مثال نیز از فرمول گاز ایدهال استفاده میکنیم:
$$PV = n RT$$
از آنجا که تعداد مولها ثابت است، از قانون ترکیبی گازها استفاده میکنیم:
$$ \frac{P_1 V_ 1}{ T _1} = \frac{P_2 V_ 2}{ T _ 2}$$
$$P_1$$ و $$V_1$$ و $$T_1$$ فشار، حجم و دما قبل از پرواز بالن و $$P_2$$ و $$V_2$$ و $$T_2$$ فشار، حجم و دمای بالون در ارتفاع ۳۲ کیلومتری از سطح زمین و قبل از ترکیدن آن هستند.
$$P_ 1 = 765 \ Torr , \enspace P_2 = 6.51 \ Torr\\ V_1 = 1.85 \times 10 ^ 3 \ L , \enspace V_ 2 = ? \\ T_ 1 = 290 \ K , \enspace T _ 2 = 229 \ K$$
برای بهدست آوردن $$V_2$$، رابطه $$ \frac{P_1 V_ 1}{ T _1} = \frac{P_2 V_ 2}{ T _ 2}$$ را برحسب $$V_2$$ مرتب میکنیم:
$$V_2 = \frac { P _ 1 V_ 1 T_ 2 } { T_ 1 P _ 2 } $$
با جایگذاری مقدارهای داده شده در رابطه بالا، حجم بالون قبل از ترکیدن برابر $$1.68 \times 10 ^ 5$$ لیتر بهدست میآید.
مثال محاسبه فشار جزیی
محفظهای ۱۰ لیتری از ۷/۶۰ گرم گاز آرگون و ۴/۴۰ گرم گاز نیتروژن تشکیل شده است. اگر دمای محفظه برابر ۲۵ درجه سلسیوس باشد، فشار جزیی هر گاز و فشار کل داخل محفظه را بهدست آورید.
پاسخ
در مطالب بالا در مورد فشار جزیی و تفاوت آن با فشار کل صحبت کردیم. فرمول گاز کامل برابر است با:
$$PV = nRT$$
در این مثال میخواهیم فشار را بهدست آوریم، بنابراین رابطه فوق را برحسب فشار مرتب میکنیم:
$$P = \frac { n R T } { V}$$
فشار جزیی گاز آرگون با استفاده از رابطه زیر بهدست میآید:
$$P _ {Ar} = \frac { n_ { Ar } R T } { V }$$
همچنین، فشار جزیی گاز نیتروژن نیز با استفاده از رابطه زیر بهدست میآید:
$$P _ { N_2 } = \frac { n_ { N _ 2 } R T } { V }$$
ثابت جهانی گازها، R، برحسب واحدهای مختلف برابر است با:
$$R = 8.314 \ J \ mol ^ { -1 } \ K ^ { -1 } \\ = 0.08206 \ L \ atm \ mol ^ { -1 } \ K ^ { -1 } \\ = 62.36 \ L \ Torr \ mol ^ { -1 } \ K ^ { -1 } \\ 1 \ atm = 760 \ mm \ Hg = 760 \ Torr$$
برای محاسبه فشار جزیی هر گاز ابتدا جرم مولی هر کدام را با استفاده از جدول تناوبی بهدست میآوریم:
$$M(Ar) = 39.95 \ \frac { g } { mol } \\
M ( N_2 ) = 28.02 \ \frac { g } { mol}$$
فشار جزیی آرگون و نیتروژن برابر هستند با:
$$P_ { Ar } = \frac { 7.60 \ g \times \frac { 1 } { 39.95} \times 62.36 \ \frac { L . Torr} { mol . K } \times 298 \ K } { 10.0 \ L } = 354 \ Torr \\ P_ { N_2 } = \frac {4.40 \ g \times \frac { 1 } { 28.02} \times 62.36 \ \frac { L . Torr} { mol . K } \times 298 \ K } { 10.0 \ L } = 292 \ Torr $$
همچنین، فشار کل برابر است با:
$$P _ { tot} = P _ { Ar } + P _ {N _ 2 } \\ P _{ tot} = 354 \ Torr + 292 \ Torr = 646 \ Torr$$
در بخش قبل با مهمترین فرمول های ترمودینامیک برای گاز کامل آشنا شدیم. در بخش بعد در مورد فرمول های ترمودینامیک برای گاز واقعی صحبت میکنیم.
فرمول های ترمودینامیک برای گاز واقعی
در بخش قبل در مورد گاز ایدهال و فرمول های ترمودینامیک حاکم بر آن صحبت کردیم. گرچه مدل گاز ایدهال اطلاعات نسبتا درستی در مورد رفتار گازها به ما میدهد، باید بدانیم هیچ گازی به طور کامل ایدهال نیست. هنگامیکه در مورد گاز کامل صحبت میکنیم، رابطه $$PV = nRT$$ تغییر خواهد کرد. قبل از صحبت در مورد گاز واقعی، ویژگیهای گاز کامل را با یکدیگر بررسی میکنیم:
- مولکولهای گاز کامل هیچ فضایی را اشغال نمیکنند.
- هیچ نیروی بین مولکولی بین مولکولهای تشکیلدهنده گاز کامل وجود ندارد.
- برخورد مولکولهای گاز کامل با یکدیگر از نوع برخورد کشسانی است.
اما در گاز واقعی:
- مولکولهای گاز فضای مشخصی را اشغال میکنند. شیمیدانی هلندی به نام «واندروالس» (Van Der Waal) این نکته را به هنگام بهدست آوردن رابطه حاکم بر گاز کامل لحاظ کرد.
- برخلاف گاز کامل که در آن مولکولها هیچ نیرویی بر یکدیگر وارد نمیکنند، مولکولهای تشکیلدهنده گاز واقعی نیروی کوچکی به نام نیروی واندروالس بر یکدیگر وارد میکنند. واندروالس به این نتیجه رسید که میزان انحراف فرمول گاز کامل از فرمول گاز ایدهال به بزرگی نیروهای بینمولکولی و اندازه هر مولکول بستگی دارد.
محفظهای را در نظر بگیرید که از تعداد زیادی ذره تشکیل شده است. اگر تمام ذرات داخل محفظه توسط نیروی جاذبه یکدیگر را جذب کنند، چه اتفاقی رخ میدهد؟مولکولهای تشکیلدهنده گاز در صورت برخورد با یکدیگر میتوانند در نوعی از برهمکنش الکترواستاتیکی شرکت کنند. در گاز ایدهال از برخورد مولکولهای گاز با یکدیگر و اندازه فیزیکی آنها صرفنظر میکنیم زیرا از این دو مورد میتوان در فشار اتمسفر صرفنظر کرد. اما به این نکته باید توجه داشته باشید که در شرایطی خاص نمیتوانیم این دو مورد را نادیده بگیریم.
در این حالت، با گاز واقعی مواجه میشویم. گاز واقعی باید بسیار پراکنده باشد یا باید حجم آن در مقایسه با حجم اشغال شده توسط ذرات گاز بسیار بزرگتر باشد. در این حالت میتوانیم از حجم ذرات صرفنظر و با آنها همانند ذرات رفتار کنیم. اما اگر گاز تا جایی فشرده شود که ذرات تشکیلدهنده آن در فاصله بسیار نزدیکی نسبت به یکدیگر قرار بگیرند و حجم قابلمقایسهای از کل حجم را اشغال کنند، از حجم ذرات نمیتوان چشمپوشی کرد. این بدان معنا است که اگر فشار به اندازه کافی افزایش یابد، قانون گاز ایدهال دیگر برقرار نخواهد بود.
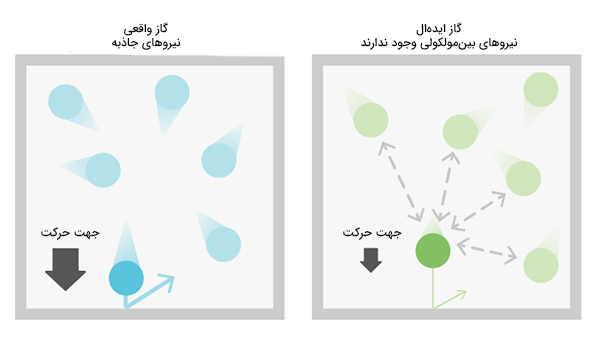
ذرات تشکیلدهنده گاز ایدهال با سرعت نسبتا زیادی حرکت میکنند. اگر این ذرات از کنار یکدیگر عبور کنند با احتمال کمی به یکدیگر برخورد خواهند کرد. اما اگر گاز فشرده شود و دما تا جایی کاهش یابد که ذرات با سرعت بسیار کوچکتری حرکت کنند، در صورت عبور از کنار یکدیگر با احتمال بالایی با یکدیگر برخورد خواهند کرد.در این حالت برهمکنش بین ذرات ممکن است از نوع برهمکنش پراکندگی یا برهمکنش دوقطبی-دوقطبی باشد. این بدان معنا است که اگر دما به اندازه کافی کاهش یابد، قوانین گاز ایدهال برقرار نخواهند بود.
در نتیجه، در فشارهای بالا و دماهای پایین، گاز رفتار ایدهال از خود نشان نمیدهد. گرچه توصیف رفتار گاز ایدهال به صورت کمی بسیار سخت است، اما با استفاده از معادله واندروالس تا حدودی میتوانیم رفتار گاز واقعی را به خوبی توصیف کنیم. برای نوشتن معادله واندروالس از معادله گاز ایدهآل شروع میکنیم و دو ضریب تصحیح را به این معادله اضافه میکنیم. معادله گاز ایدهآل به صورت زیر نوشته میشود:
$$PV=n R T$$
ابتدا فشار گاز را با اضافه کردن عبارت $$\frac { a n ^ 2 } { V ^ 2 }$$ اصلاح میکنیم. این عبارت به جاذبه بین ذرات تشکیلدهنده گاز مربوط میشود. a در این عبارت ثابتی است که قدرت نیروی جاذبه بین ذرات گاز را توصیف میکند. مقدار این نیرو با نوع ذرات تشکیلدهنده گاز ارتباط دارد. هرچه مولکولها بزرگتر و قطبیدهتر باشند، نیروی جاذبه بین آنها قویتر خواهد بود. در مقابل، نیروی جاذبه بین مولکولهای غیرقطبی و کوچکتر، کمتر است.
همچنین، n و $$V$$ به ترتیب مول و حجم هستند. در ادامه، عبارت $$nb$$ را از حجم کم میکنیم. $$nb$$ حجم اشغال شده توسط ذرات گاز است. در نتیجه، معادله گاز واقعی، معادله واندروالس، به صورت زیر نوشته میشود:
$$( P + \frac { a n ^ 2 } { V ^ @ } ) ( V - nb ) = n R T$$
در این معادله:
- b اندازه ذرات تشکیلدهنده گاز را توصیف میکند. مقدار آن به نوع ذرات تشکیلدهنده گاز بستگی دارد.
- n، مول است.
با مقایسه دو معادله گاز ایدهال و واندروالس مشاهده میکنیم که سمت راست دو معادله، $$nRT$$، با یکدیگر برابر هستند و بدون تغییر باقی میمانند. مقدارهای a و b برای هر گاز منحصربهفرد است. مقدارهای a و b برای تعدادی از گازهای معروف در جدول زیر نوشته شدهاند.
| ماده | $$a ( L ^ 2 - \ atm / mol ^ 2 )$$ | $$b \ ( L / mol)$$ |
| He | ۰/۰۳۴۱ | ۰/۰۲۳۷۰ |
| Ne | ۰/۲۱۱ | ۰/۰۱۷۱ |
| Ar | ۱/۳۴ | ۰/۰۳۲۲ |
| Kr | ۲/۳۲ | ۰/۰۳۹۸ |
| Xe | ۴/۱۹ | ۰/۰۵۱۰ |
| $$H_2$$ | ۰/۲۴۴ | ۰/۰۲۶۶ |
| $$N_2$$ | ۱/۳۹ | ۰/۰۳۹۱ |
| $$O_2$$ | ۱/۳۶ | ۰/۰۳۱۸ |
| $$Cl_2$$ | ۶/۴۹ | ۰/۰۵۶۲ |
سوالی که ممکن است مطرح شود آن است که معادله واندروالس تحت چه شرایطی به شکل معادله گاز ایدهال درمیآید. معادله واندروالس تحت شرایط حاکم بر گاز ایدهال به شکل معادله $$PV= nRT$$ نوشته میشود. اگر حجم بسیار بزرگ و تعداد مولها بسیار کوچک باشند، گازی پراکنده خواهیم داشت. در این حالت میتوانیم گاز را نزدیک به گاز ایدهال در نظر بگیریم. بنابراین، عبارتهای تصحیحی $$\frac { a n ^ 2 } { V ^ 2 } $$ و $$nb$$ به سمت صفر میل میکنند و معادله واندروالس به شکل معادله گاز ایدهال نوشته میشود.
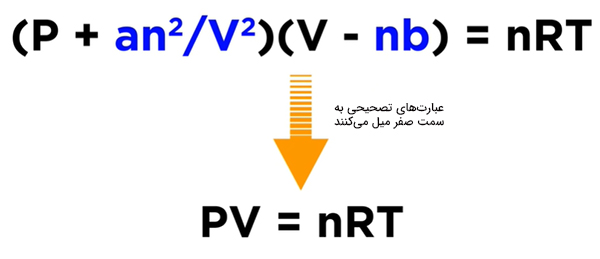
استفاده از معادله واندروالس به هنگام دور شدن از شرایط گاز ایدال تا چه اندازه اهمیت دارد؟ برای پاسخ به این پرسش گازی را به عنوان نمونه انتخاب میکنیم و محاسبات یکسانی را با فرمولهای گاز ایدهال و واندروالس انجام میدهیم. برای انجام این کار فرض کنید محفظهای به حجم ۴/۲۵ لیتر حاوی ۳/۴۶ مول گاز دیاکسیدکربن در دمای ۲۲۹ درجه سلسیوس داریم. فشار گاز چه مقدار است؟
استفاده از معادله گاز ایدهال برای محاسبه فشار
در حالت نخست از معادله گاز ایدهال برای محاسبه فشار گاز استفاده میکنیم:
$$PV = nRT$$
معادله فوق را برحسب فشار مرتب میکنیم:
$$P = \frac { n R T } { V }$$
مقدارهای داده شده را در معادله بالا قرار میدهیم و مقدار فشار را بهدست میآوریم:
$$P = \frac { n R T } { V } \\ P = \frac { ( 3.46 \ mol ) ( 0.0821 \ L \ atm / mol \ K ) ( 502 \ K ) } { 4.25 \ L } = 33.3 \ atm$$
استفاده از معادله واندروالس برای محاسبه فشار
در حالت دوم از معادله واندروالس برای محاسبه فشار استفاده میکنیم:
$$( P + \frac { a n ^ 2 } { V ^ 2 } ) ( V - nb) = n R T$$
معادله فوق را برحسب فشار مرتب میکنیم:
$$P = \frac { n R T } { V - nb } - \frac { a n ^ 2 } { V ^ 2 }$$
مقدارهای a و b برای گاز دیاکسیدکربن به ترتیب برابر $$3.59 \ \frac { L ^ 2 \ atm } { mol ^ 2 }$$ و $$ 0.0427 \ \frac { L } { mol }$$ هستند. مقدارهای داده شده برای حجم، تعداد مول، دما، a و b را در رابطه فشار قرار میدهیم:
$$P = \frac { ( 3. 46 \ mol ) ( 0.0821 \ \frac { L \ atm } { mol \ K } ) ( 502 \ K) } { 4.25 \ L - ( 3.46 \ mol ) ( 0.0427 \ \frac { L } { mol } ) } - \frac { ( 3.59 \ \frac { L ^ 2 \ atm }{ mol ^ 2 } ) ( 3.46 \ mol ) ^ 2 } { ( 4.25 ) ^ 2 }= 32.4 \ atm$$
همانطور که دیدیم فشار بهدست آمده از رابطه گاز ایدهال برابر ۳۳/۵ اتمسفر و فشار بهدست آمده از معادله واندروالس برابر ۳۲/۴ اتمسفر است. فشار بهدست آمده با استفاده از معادله واندروالس دقیقتر است. اما فشار بهدست آمده با استفاده از معادله گاز ایدهال نیز به مقدار بهدست آمده توسط معادله واندروالس بسیار نزدیک است. در واقع فشارهای بهدست آمده با استفاده از این دو معادله اختلاف چشمگیری با یکدیگر ندارند زیرا در این مثال، فشار محفظه خیلی بالا نیست. هرچه مقدار فشار بالاتر باشد، انحراف از گاز ایدهال چشمگیرتر خواهد بود. همچنین، مولکول دیاکسیدکربن غیرقطبی است. از اینرو، نیروی جاذبه خیلی بزرگ نیست. اگر به جای مولکول غیرقطبی دیاکسید کربن، از مولکول قطبی مانند مولکولهای آلی استفاده میکردیم، معادله گاز ایدهال توصیف صحیحی از شرایط حاکم بر سیستم ارائه نمیداد.
پرسش
تحت چه شرایطی نمیتوانیم گاز را به صورت گاز ایدهال درنظر بگیریم؟
پاسخ
رفتار گاز در فشارهای بالا و دماهای کم از رفتار گاز ایدهال فاصله میگیرد.
معادله واندروالس را برحسب فشار مرتب میکنیم:
$$P = \frac { n R T } { V - n b } - \frac { a n ^ 2 } { V ^ 2 }$$
عبارت nb مربوط به در نظر گرفتن اندازه متناهی برای مولکولهای تشکیلدهنده گاز و عبارت تصحیحی $$\frac { a n ^ 2 } { V ^ 2 }$$ مربوط به در نظر گرفتن نیروی جاذبه بین مولکولهای گاز است. همانطور که در مطالب بالا دیدیم معادله واندروالس در مقایسه با معادله گاز ایدهال، توصیف دقیقتری از رفتار گاز به ما میدهد. به این نکته توجه داشته باشید که a و b تجربی هستند. بنابراین، مقدار آنها با انجام آزمایشهای مرتبط به دست میآید. معادلههای گاز ایدهال و واندروالس دو معادله برای توصیف رفتار گازها هستند. اما هیچ یک از آنها به طور کامل و دقیق نمیتوانند رفتار گازهای مختلف را توصیف کنند. از اینرو، مدلهای دیگری برای توصیف رفتار گازها نوشته شدند.
مدل ردلیش کوانگ
معادله «ردلیش کوانگ» (Redlich-Kwang) یکی از فرمول های ترمودینامیکی مهم است. این فرمول به صورت زیر نوشته میشود:
$$P = \frac {RT} {V - b} - \frac {a } {(V(V + b) \times √T)}
$$
در این معادله:
- P فشار گاز را نشان میدهد.
- V حجم محفظه حاوی گاز را نشان میدهد.
- T دمای گاز است.
- R ثابت جهانی گازها است.
- a و b ثابتهای مربوط به هر گاز هستند و مقدار آنها با تغییر گاز، تغییر میکند.
توجه به این نکته مهم است که عبارت $$\frac {RT} {V - b}$$ در معادلههای واندروالس و ردلیش کوانگ یکسان است.
مدل پنگ رابینسون
معادله «پنگ رابینسون» (Peng-Robinson) به صورت زیر نوشته میشود:
$$P = \frac {RT} {V - b} - \frac {a [ 1 + k( 1 - \sqrt {\frac {T } {T _C}})^ 2] } {(V(V + b) +b( V - b)}
$$
در این معادله، علاوه بر ثابتهای a و b، ثابت دیگری به نام k نیز وجود دارد. $$T_c$$ در معادله پنگ رابینسون، دمای بحرانی نام دارد. این معادله در مقایسه با دو معادله واندروالس و ردلیش کوانگ رفتار گاز را دقیقتر توصیف میکند. مدلهای دیگری نیز برای توصیف دقیقتر گازهای واقعی وجود دارند که از جملههای بیشتر و پیچیدهتری تشکیل شدهاند.
معادله ویریال
معادله ویریال یکی از مهمترین فرمول های ترمودینامیک در فیزیک و مهندسی است. نمودار همدمای گازی در حالت ایدهال و در حالت تجربی در تصویر زیر نشان داده شدهاند. همانطور که در تصویر زیر دیده میشود، دو نمودار در فشارهای کم و حجم زیاد به یکدیگر بسیار نزدیک هستند. هر چه حجم کمتر و فشار بیشتر شود، فاصله نمودار تجربی از نمودار ایدهال افزایش مییابد. به بیان دیگر، رفتار گاز از گاز ایدهال فاصله میگیرد. بنابراین، همانطور که در مطالب بالا خواندیم در فشارهای بالا و حجمهای کوچک، گاز رفتار ایدهال از خود نشان نمیدهد.
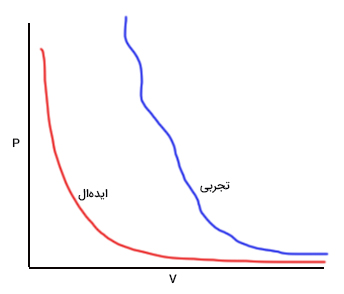
معادله گاز ایدهال آغاز خوبی برای توصیف رفتار گازها است. در معادله ویریال از معادله گاز ایدهال به عنوان اولین تقریب و برای تقریبهای بعدی از سری توانی استفاده میکنیم. در نتیجه، معادله ویریال به صورت زیر نوشته میشود:
$$P\overline{V} = RT ( 1 + B P + C P ^ 2 + ...)
$$
در معادله فوق:
- $$\overline{V}$$، حجم مولی و برابر نسبت حجم به تعداد مولهای گاز است.
- ثابتهای B و C، ثابتهای ویریال هستند.
سری توانی در معادله فوق برحسب فشار نوشته شده است. در بسیاری از کاربردها، سری توانی برحسب حجم و به صورت زیر نوشته میشود:
$$P\overline{V} = RT ( 1 + \frac { B } { \overline { V }} + \frac { C } { \overline { V }^ 2} + ...)
$$
به طور معمول، به هنگام استفاده از دو معادله بالا، تنها تا جمله دوم یا سوم را در نظر میگیریم و از جملههای با توان بالاتر صرفنظر میکنیم. ضریب Z به نام ضریب فشردگی را به صورت زیر تعریف میکنیم:
$$Z = \frac { (PV) _ { real \enspace gas }} { ( P V ) _ { ideal \enspace gas }} = \frac { PV } { n R T } = \frac { P \overline V } { R T }$$
$$Z = ( 1 + \frac { B } { \overline { V }} + \frac { C } { \overline { V }^ 2} + ...)$$
با استفاده از Z راحتتر میتوانیم جملههای با توان بالاتر را توصیف کنیم. ضریب فشردگی به ما میگوید رفتار گاز واقعی چگونه از رفتار گاز ایدهال فاصله میگیرد. بنابراین، سری توانی نوشته شده به طور فیزیکی تمام برهمکنشهایی که سبب انحراف رفتار گاز واقعی از گاز ایدهال میشود را جمعآوری میکند. ضریب فشردگی را برای معادله واندروالس به صورت زیر بهدست میآوریم:
$$P = \frac { n R T } { V - n b } - \frac { a n ^ 2 } { V ^ 2} \\ P = \frac { RT } { \frac { V } { n } - b} - \frac { a } { ( \frac { V } { n } ) ^ 2 }\\ P = \frac { R T } { \overline { V } - b } - \frac { a } { \overline V } \\ Z = \frac { P \overline V } { R T } = \frac { \frac { R T } { \overline { V } - b } - \frac { a } { \overline V }} { RT } \\ Z = \frac { \overline { V }} { \overline {V } - b } - \frac { a } { R T \overline { V } }$$
Z را برحسب سری توانی مینویسیم. برای انجام این کار جمله $$\frac { \overline { V }} { \overline {V } - b }$$ را به صورت زیر مینویسیم:
$$\frac { \overline { V }} { \overline {V } - b } = \frac { \overline { V } } { \overline { V } ( 1 - \frac { b } { \overline { V } } )} = \frac { 1 } {1 - \frac { b } { \overline { V } }}$$
بنابراین، Z به صورت زیر نوشته میشود:
$$ Z= \frac{ 1 }{ ( 1 - \frac{b}{\overline { V }}) } - \frac{a}{ R \ T \ \overline { V }}$$
برای آنکه بتوانیم Z را به صورت سری توانی بنویسیم از سری مک لورن که به صورت زیر نوشته میشود استفاده میکنیم:
$$\frac{ 1 }{1- x} = 1 + x + x ^ 2 + ...$$
از اینرو، کسر $$ \frac{ 1 }{ ( 1 - \frac{b}{\overline { V }}) }$$ به صورت زیر نوشته میشود:
$$\frac{ 1 }{ ( 1 - \frac{b}{\overline { V }}) } = 1 + ( \frac{b}{\overline { V }}) + + ...$$
کسر $$ \frac{ 1 }{ ( 1 - \frac{b}{\overline { V }}) }$$ را تا جمله $$ ( \frac{b}{\overline { V }})$$ بسط میدهیم. در نتیجه، Z به شکل زیر نوشته خواهد شد:
$$Z \approx 1 + ( \frac{b}{\overline { V }}) - \frac{ a }{R \ T \ \overline { V }}$$
با استفاده از رابطه بهدست آمده برای Z میتوانیم دومین ضریب ویریال را بهدست آوریم. برای انجام این کار از $$\frac { 1 } { \overline { V } }$$ فاکتور میگیریم:
$$Z \approx 1 + ( b- \frac { a } { RT }) (\frac { 1 } { \overline { V } })$$
بنابراین، دومین ضریب ویریال، B، برابر $$( b- \frac { a } { RT })$$ بهدست میآید. با استفاده از این ضریب میتوانیم میزان انحراف رفتار گاز واقعی از گاز ایدهال را بهدست آوریم. همانطور که در رابطه بهدست آمده برای B مشاهده میکنیم a و b و R ثابت هستند. بنابراین، B تنها با دما تغییر میکند. اگر دومین ضریب ویریال برابر صفر باشد، گازی داریم که همانند گاز ایدهال رفتار خواهد کرد. سوالی که ممکن است مطرح شود آن است که این ضریب چه زمانی برابر صفر میشود. ضریب B در دمایی به نام دمای بویل برابر صفر میشود. به بیان دیگر، به دمایی که در آن دومین ضریب ویریال برابر صفر میشود، دمای بویل میگوییم. این دما به صورت زیر بهدست میآید:
$$b- \frac { a } { RT } = 0 \\ T = \frac { a } { R b }$$
اثبات مفهومی معادله واندروالس
در مطالب بالا با معادله واندروالس و تفاوت گاز ایدهال با گاز واندروالس آشنا شدیم. سوالی که ممکن است مطرح شود آن است که معادله واندروالس چگونه بهدست آمد. در این بخش، معادله واندروالس را به صورت مفهومی توضیح میدهیم. همانطور که اشاره شد مولکولها در گاز ایدهال، فضایی را اشغال نمیکنند و هیچ نیروی بین مولکولی بین آنها وجود ندارد. مولکولها در گاز واقعی فضا اشغال میکنند. فضای اشغال شده میکروسکوپی، اما واقعی است. واندروالس انحراف رفتار گاز واقعی از گاز ایدهال را مطالعه کرد. او به این نتیجه رسید که مولکولها در گاز واقعی بر یکدیگر نیرو وارد میکنند. به این نیرو، نیروی واندروالس گفته میشود. واندروالس به این نتیجه رسید که میزان انحراف رفتار گاز واقعی از گاز ایدهال به قدرت نیروی بین مولکولها و اندازه آنها وابسته است.
سیستمی حاوی تعدادی مولکول را در نظر بگیرید. اگر این ذرات یکدیگر را جذب کنند، چه اتفاقی رخ میدهد؟ در این حالت فشار تحتتاثیر قرار میگیرد. در گاز واقعی باید تاثیر نیروهای بینمولکولی را در نظر بگیریم. نخستین سوالی که مطرح میشود آن است که نیروهای بینمولکولی به چه عواملی وابسته هستند. برخی از این نیروها به غلظت ذرات بستگی دارند، زیرا هرچه تعداد ذرات تشکیلدهنده گاز بیشتر باشد، نیروی جاذبه بیشتری نیز وارد خواهد شد. غلظت هر ماده برابر مقدار ماده بر مقدار فضای اشغال شده توسط آن است. مقدار مولکولهای تشکیلدهنده گاز برابر n (تعداد مول) و فضای اشغال شده توسط آنها برابر $$V$$ است. بنابراین، غلظت گاز برابر $$\frac { n } { V}$$ خواهد بود.

رابطه $$\frac { n } { V}$$ زمانی صحیح است که تمام ذرات داخل گاز توسط یک ذره جذب شوند. اما ذرات تشکیلدهنده گاز توسط یکدیگر نیز جذب میشوند. بنابراین، نیروی جاذبه بین مولکولی با افزایش تعداد ذرات به طور چشمگیری افزایش مییابد. از اینرو، عبارت $$\frac { n } { V}$$ را به توان دو میرسانیم. توجه به این نکته مهم است که نوع ذره بر مقدار نیروی جاذبه بینمولکولی تاثیر میگذارد. بنابراین، باید ویژگی ذرات مختلف را در نظر بگیریم و آن را بر نیروی جاذبه بینمولکولی اعمال کنیم. هر گاز یک عامل ذاتی به نام a دارد که باید در نظر گرفته شود. a را میتوانیم ضریب جذب بنامیم. مقدار a برای هر گاز منحصربهفرد است و از گازی به گاز دیگر تغییر میکند. با توجه به مطالب بیان شده، فشار گاز واقعی برابر است با:
$$P_0 + a [ \frac { n } { V } ] ^ 2 $$
به این نکته توجه داشته باشید که ذرات تشکیلدهنده گاز نهتنها یکدیگر را جذب میکنند، بلکه ممکن است توسط نیرویی دافعه از یکدیگر دور شوند. از اینرو، مقدار a میتواند منفی یا مثبت باشد. فرض مهم دیگر در گاز ایدهال آن است که ذرات تشکیلدهنده ان فضایی را اشغال نمیکنند. اما در حالت واقعی اینگونه نیست. بنابراین، حجم در نظر گرفته شده برای گاز ایدهال باید اصلاح شود. هر گاز از ذراتی با اندازههای مختلف تشکیل شده است. به عنوان مثال، ذرات هیدروژن بسیار کوچک و ذرات متان نسبتا بزرگ هستند. در نتیجه، هر گاز حجم تجربی مشخصی به نام b دارد که باید در نظر گرفته شود. b را در تعداد مول گاز ضرب میکنیم. بنابراین، حجم اصلاح شده برای گاز واقعی برابر تفاضل حجم محفظه گاز و حجم اشغال شده توسط ذرات گاز است:
$$V_c - nb$$
برخلاف a، ضریب b همواره مثبت است. در ادامه، فشار و حجم اصلاح شده را در معادله گاز کامل قرار میدهیم:
$$(P + a [ \frac { n } { V } ] ^ 2 )(V_c - nb) = n R T$$
در بخش قبل با مهمترین فرمول های ترمودینامیک برای گاز واقعی، مانند فرمول واندروالس، آشنا شدیم. در ادامه، فرمول های ترمودینامیک در قانون اول را بیان میکنیم.
فرمول های ترمودیناک در قانون اول
در این بخش، قانون اول ترمودینامیک را به صورت خلاصه توضیح میدهیم و در مورد روابط حاکم بر این قوانین و اثبات ریاضی آنها صحبت میکنیم.
قانون اول ترمودینامیک چیست ؟
قانون اول ترمودینامیک در مورد انرژی درونی، کار و گرما و رابطه بین آنها صحبت میکند. به بیان دیگر، قانون اول ترمودینامیک بیان دیگری از قانون پایستگی انرژی است. بر طبق این قانون، انرژی نه به وجود میآید، نه از بین میرود، بلکه از حالتی به حالت دیگر تبدیل میشود. فرض کنید سیستمی فرضی داریم که توسط محیط اطراف احاطه شده است. انرژی میتواند به سیستم وارد یا از آن خارج شود. دو راه برای انتقال انرژی به درون سیستم یا خروج انرژی از آن وجود دارند:
- گرما
- کار
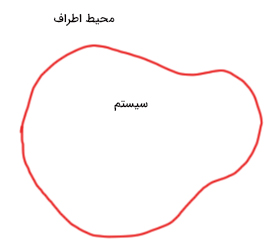
اگر گرما به سیستم وارد شود، سیستم انرژی بهدست میآورد. به این انرژی، انرژی درونی سیستم میگوییم و آن را با $$U$$ نشان میدهیم. محیط اطراف میتواند روی سیستم کار انجام دهد. بنابراین، انرژی درونی سیستم با ورود گرما به آن یا انجام کار توسط محیط اطراف روی سیستم افزایش مییابد. سیستمها به سه دسته تقسیم میشوند:
- سیستم باز: ماده و گرما میتوانند به این سیستم وارد یا از آن خارج شوند.
- سیستم بسته: ماده نمیتواند به این سیستم وارد یا از آن خارج شود، اما انرژی میتواند.
- سیستم ایزوله: ماده و انرژی نمیتوانند به این سیستم وارد یا از آن خارج شوند. بنابراین، جرمِ داخلِ سیستم ایزوله و انرژی کل آن ثابت باقی میمانند.
تغییرات انرژی درونی سیستم، $$\triangle U$$، برابر جمع انرژی گرمایی و کار است:
$$\triangle U = Q + W$$
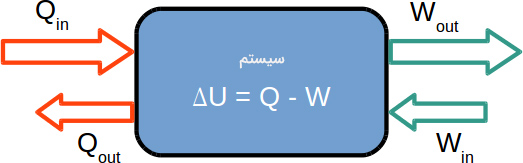
معادله فوق را در بیشتر کتابهای شیمی مشاهده میکنیم. $$Q$$ انرژی گرمایی وارد شده یا خارج شده از سیستم و $$W$$ کار را نشان میدهند. در فیزیک، معادله فوق کمی متفاوت نوشته میشود:
$$\triangle U = Q - W$$
دلیل این تفاوت به انتخاب دیدگاه فیزیک و شیمی بستگی دارد. در شیمی، سیستم از توجه ویژهای برخوردار است و انتقال انرژی و کار از دیدگاه سیستمی بررسی میشود. در مقابل، در فیزیک محیط اطراف از توجه ویژهای برخوردار است و انتقال انرژی و کار از دیدگاه محیطی بررسی خواهد شد. بنابراین در شیمی:
- اگر سیستم کار انجام دهد، کار منفی است.
- اگر کار توسط محیط اطراف روی سیستم انجام شود، علامت کار مثبت در نظر گرفته میشود.
اما در فیزیک:
- اگر سیستم کار انجام دهد، کار مثبت است.
- اگر کار توسط محیط اطراف روی سیستم انجام شود، علامت کار منفی در نظر گرفته میشود.
فرمول های ترمودینامیک در قانون اول و اثبات آن ها
در این بخش، مهمترین فرمولهای قانون اول ترمودینامیک را بهدست میآوریم. این فرمولها از دو کمت بسیار مهم به نام انرژی درونی ($$U$$) و آنتالپی ($$H$$) تشکیل شدهاند. انرژی درونی را در بخش قبل به صورت رابطه $$\triangle U = Q - W$$ تعریف کردیم. این رابطه را میتوانیم به شکل دیفرانسیلی بنویسیم.
$$dU = dQ - dU$$
ویژگی مهم انرژی درونی آن است که آن را به صورت تابع حالت در نظر میگیریم. به این نکته توجه داشته باشید که آنتالپی نیز تابع حالت است. گرچه انرژی درونی را به عنوان تابع حالت میشناسیم، انرژی گرمایی و کار لزوما تابع حالت نیستند. انرژی درونی تابعی از فشار، دما و حجم است:
$$U = U ( P, \ T, \ V)$$
به دلیل آنکه که کمیتهای فشار، دما و حجم توسط معادلات حالت به یکدیگر مربوط میشوند، انرژی درونی را میتوان به صورت تابعی از دما و حجم نوشت:
$$U = U ( P, \ T, \ V) = U ( T , \ V)$$
از آنجا که انرژی درونی را میتوانیم به صورت تابعی از دو متغیر بنویسیم و به دلیل آنکه $$U$$ تابع حالت است، آن را میتوانیم به شکل دیفرانسیل کامل بنویسیم:
$$d U$$
شاید از خود بپرسید چرا تابع حالت را میتوانیم به شکل دیفرانسیل کامل بنویسیم. قبل از اثبات فرمول های ترمودینامیک در قانون اول، خالی از لطف نیست کمی در مورد تابع حالت توضیح دهیم.
تابع حالت چیست ؟
تابع حالت تابعی است که مقدار نهایی آن به مسیر طی شده توسط آن وابسته نیست. به بیان دیگر، مقدار نهایی تابع حالت مستقل از مسیر طی شده توسط آن است. توابع حالت را میتوانیم از دیدگاه انتگرالی نیز بررسی کنیم. انتگرالها تنها به سه مورد بستگی دارند:
- تابع
- حد پایین انتگرال
- حد بالای انتگرال
به طور مشابه، توابع حالت به سه عامل بستگی دارند:
- ویژگی
- مقدار اولیه
- مقدار نهایی
به بیان دیگر، انتگرالها نشان میدهند چگونه تابعهای حالت، تنها به مقدار اولیه و نهایی وابسته و مستقل از مسیر بین مقدار اولیه تا نهایی هستند. به عنوان مثال، انتگرال آنتالپی به صورت زیر نوشته میشود:
$$\int_{ t _ 0 }^{t _ 1} H (t ) dt = H (t _1 ) - H ( t _ 0 )$$
تعریف فوق معادل تعریف آشنای آنتالپی است:
$$\triangle H = H _ { final} - H _ {intial}$$
با توجه به رابطههای نوشته شده در بالا، آنتالپی تابع حالت است زیرا تنها شرایط اولیه و نهایی بستگی دارد و مستقل از مسیر طی شده برای رسیدن از حالت ابتدا به حالت پایانی است. بنابراین، تابع حالت مستقل از مسیر است. نکته مهم دیگر آن است که مهم نیست در مورد جرم، مول، حجم یا متغیرهای مشابه صحبت میکنیم، در ترمودینامیک، تنها تغییرات انرژی از اهمیت ویژهای برخوردار است. در تغییر از حالت A به حالت B، تنها تغییر انرژی مهم است و به تغییرات تعداد مول بین دو حالت یا تغییرات ماده اهمیت نمیدهیم.
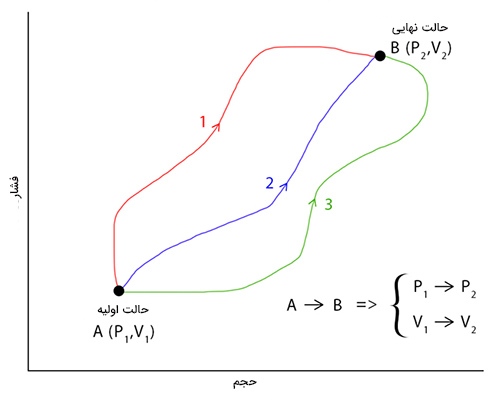
تا اینجا میدانیم تابع حالت چیست و در تغییر بین دو حالت چگونه نوشته میشود. همچنین، همانطور که در مطالب بالا اشاره شد، انرژی درونی سیستم، تابع حالت و وابسته به متغیرهای دما و حجم است. همچنین، گفتیم انرژی درونی را میتوانیم به صورت دیفرانسیل کامل بنویسیم. در نتیجه، $$dU$$ به شکل زیر نوشته میشود:
$$dU = (\frac{\partial U}{\partial T}) _ V \ dT + (\frac{\partial U}{\partial P} ) _ P\ dV $$
به این نکته توجه داشته باشید که انرژی درونی تابعی از دو متغیر دما و حجم است، بنابراین هنگامی که مشتق آن را نسبت به یکی از متغیرها، به عنوان مثال فشار، میگیریم و متغیر دیگر، مانند حجم، را ثابت نگه میداریم، مشتق جزیی انرژی درونی به صورت زیر نوشته خواهد شد:
$$(\frac{\partial U}{\partial T}) _ V $$
عبارت $$(\frac{\partial U}{\partial T}) _ V $$ برابر ظرفیت گرمایی در حجم ثابت است و به صورت زیر نوشته میشود:
$$(\frac{\partial U}{\partial T}) _ V = C_ V$$
همانطور که در رابطه $$dU = (\frac{\partial U}{\partial T}) _ V \ dT + (\frac{\partial U}{\partial P} ) _ P\ dV $$ دیده میشود، مشتق جزیی $$U$$ یک بار در حجم ثابت و یک بار در دمای ثابت گرفته شده است. دمای ثابت یکی از شرایط مهم در ترمودینامیک است و به آن شرایط همدما یا «ایزوترمال» (isothermal) گفته میشود. دو شرایط مهم دیگر نیز به نام شرایط همحجم و همفشار نیز در ترمودینامیک داریم.
عبارت دوم در رابطه $$dU = (\frac{\partial U}{\partial T}) _ V \ dT + (\frac{\partial U}{\partial P} ) _ P\ dV $$ ، یعنی $$(\frac{\partial U}{\partial V}) _ T $$، برابر کمیتی به نام فشار داخلی است و به صورت زیر نوشته میشود:
$$(\frac{\partial U}{\partial T}) _ V = \Pi_ T$$
با توجه به تعریف کمیتهای ظرفیت گرمایی در حجم ثابت و فشار داخلی، $$dU$$ را میتوان به صورت زیر نوشت:
$$dU = C_v dT + \Pi_T dV$$
با توجه به رابطه بالا، تغییرات انرژی درونی نسبت به دما در فشار ثابت یا $$C_p$$ را بهدست میآوریم. برای انجام این کار طرفین رابطه $$dU = C_v dT + \Pi_T dV$$ را بر $$dT$$ تقسیم میکنیم:
$$\frac {dU} { dT } = C_v \frac {dT} { dT } + \Pi_T \frac {dV} { dT } $$
از آنجا که $$U$$ تابعی از چندین متغیر است، عبارت $$frac {dU} { dT }$$ باید به صورت مشتق جزیی نوشته شود:
$$\frac{\partial U}{\partial T} = C_v \frac{\partial T}{\partial T} + \Pi_T \frac{\partial V}{\partial T} $$
در ادامه، باید فشار ثابت را به رابطه بالا تحمیل کنیم. برای انجام این کار، اطراف مشتق جزییها پرانتز میگذاریم و اندیس P را پایین آنها مینویسیم.
$$(\frac{\partial U}{\partial T})_P = C_v (\frac{\partial T}{\partial T}) _ P + \Pi_T (\frac{\partial V}{\partial T} ) _ P$$
در رابطه فوق، $$(\frac{\partial T}{\partial T}) _ P$$ برابر یک است:
$$(\frac{\partial U}{\partial T})_P = C_v + \Pi_T (\frac{\partial V}{\partial T} ) _ P$$
در رابطه بهدست آمده در بالا، $$(\frac{\partial U}{\partial T})_P$$ به صورت $$C_p$$، ظرفیت گرمایی در فشار ثابت، نوشته میشود. همچنین، ضریبی به نام ضریب انبساط را به صورت زیر تعریف میکنیم:
$$alpha = \frac { 1 } { V} (\frac{\partial V}{\partial T}) _ P$$
طرفین رابطه بالا را در حجم ضرب میکنیم:
$$\alpha V = (\frac{\partial V}{\partial T}) _ P\$$
در نتیجه، رابطه $$(\frac{\partial U}{\partial T})_P = C_v + \Pi_T (\frac{\partial V}{\partial T} ) _ P $$ به صورت زیر نوشته میشود:
$$C_p = C_v + \Pi_T \alpha V$$
اثبات رابطه ضریب انبساط و تراکم پذیری هم دما
در بخش قبل با رابطه بین ظرفیت گرمایی در فشار و حجم ثابت آشنا شدیم. در این قسمت، رابطه بین ضریب انبساط گرمایی، $$\alpha$$، و تراکمپذیری همدما، $$k_T$$، را بهدست میآوریم. ضریب انبساط گرمایی و تراکمپذیری همدما با استفاده از رابطه زیر به یکدیگر مربوط میشوند:
$$(\frac{\partial P}{\partial T})_V = \frac { \alpha} { k_ T }$$
ضریب انبساط گرمایی با استفاده از رابطه زیر تعریف میشود:
$$\alpha = \frac { 1 } { V } (\frac{\partial V}{\partial T})_P$$
طرفین رابطه فوق را در $$V$$ ضرب میکنیم:
$$V \times\alpha = V \times \frac { 1 } { V } (\frac{\partial V}{\partial T})_P \rightarrow \alpha V = (\frac{\partial V}{\partial T} ) _ P$$
همچنین، تراکمپذیری همدما نیز با استفاده از رابطه زیر تعریف میشود:
$$k_T = -\ \frac { 1 } { V } (\frac{\partial V}{\partial P})_T$$
طرفین رابطه فوق را در $$- \ V$$ ضرب میکنیم:
$$- \ V \times k_T =(- \ V ) \times -\ \frac { 1 } { V } (\frac{\partial V}{\partial P})_T \rightarrow - \ k _ T V = (\frac{\partial V}{\partial P})_T$$
حجم سیستم ترمودینامیکی میتواند به صورت تابعی از دو کمیت دما و فشار تعریف شود:
$$V = V (P,T)$$
توجه به این نکته مهم است که حجم نیز همانند انرژی درونی و آنتالپی، تابع حالت است. این بدان معنا است که دیفرانسیل کامل حجم، $$dV$$، را میتوانیم به صورت زیر بنویسیم:
$$dV = (\frac{\partial V}{\partial P})_ T\ d P + (\frac{\partial V}{\partial T})_P \ d T$$
طرفین رابطه فوق را بر $$dT$$ تقسیم میکنیم:
$$\frac { dV } { d T } = (\frac{\partial V}{\partial P})_ T\ \frac { d P } { dT } + (\frac{\partial V}{\partial T})_P \ \frac { d T } { dT }$$
سپس شرایط حجم ثابت را به رابطه فوق اعمال میکنیم:
$$ (\frac{\partial V}{\partial T} ) _ V = (\frac{\partial V}{\partial P}) _ T ( \frac{\partial P}{\partial T})_V + (\frac{\partial V}{\partial T} ) _ P$$
رابطه بهدست آمده بسیار جالب است. ابتدا سمت چپ تساوی، یعنی $$(\frac{\partial V}{\partial T} ) _ V $$، را بررسی میکنیم. این عبارت به ما مشتق جزیی حجم نسبت به دما در حجم ثابت را میدهد. اما حجم را ثابت در نظر گرفتهایم، بنابراین تغییرات حجم نسبت به دما برابر صفر خواهد بود. در نتیجه، $$(\frac{\partial V}{\partial T} ) _ V $$ برابر صفر است.
$$ 0 = (\frac{\partial V}{\partial P}) _ T ( \frac{\partial P}{\partial T})_V + (\frac{\partial V}{\partial T} ) _ P$$
در ادامه، عبارت $$(\frac{\partial V}{\partial T} ) _ P$$ را از طرفین رابطه بالا کم میکنیم:
$$ - \ (\frac{\partial V}{\partial T} ) _ P = (\frac{\partial V}{\partial P}) _ T ( \frac{\partial P}{\partial T})_V + (\frac{\partial V}{\partial T} ) _ P - (\frac{\partial V}{\partial T} ) _ P \\ (\frac{\partial V}{\partial P}) _ T ( \frac{\partial P}{\partial T})_V = - \ (\frac{\partial V}{\partial T} ) _ P$$
همانطور که در ابتدای این بخش گفتیم عبارت $$\ (\frac{\partial V}{\partial T} ) _ P$$ برابر $$\alpha V$$ است:
$$(\frac{\partial V}{\partial P}) _ T ( \frac{\partial P}{\partial T})_V = - \alpha V$$
قسمتی از رابطه $$(\frac{\partial P}{\partial T})_V = \frac { \alpha} { k_ T }$$ را اثبات کردیم. در ادامه، $$k_T$$ را به آن اضافه و اثبات را تکمیل میکنیم. عبارت $$ (\frac{\partial V}{\partial P}) _ T$$ برابر $$- \ k_T V$$ است. بنابراین، در رابطه $$(\frac{\partial V}{\partial P}) _ T ( \frac{\partial P}{\partial T})_ V = - \alpha V$$ به جای عبارت $$(\frac{\partial V}{\partial P}) _ T $$، عبارت $$- \ k_T V$$ را قرار میدهیم:
$$ - \ k_T V( \frac{\partial P}{\partial T})_V = - \alpha V$$
سپس، طرفین رابطه بهدست آمده در بالا را بر $$- \ k_T V$$ تقسیم میکنیم:
$$$$\frac { - \ k_T V } { - \ k _ T V }( \frac{\partial P}{\partial T})_V = \frac {- \alpha V} { - \ k_T V }$$$$
با ساده کردن رابطه فوق به رابطه $$( \frac{\partial P}{\partial T})_V = \frac { \alpha } { \ k_T }$$ میرسیم.
بررسی ویژگی مشتق جزیی در ترمودینامیک
در این بخش، ویژگی مهم مشتق جزیی در حالت خاص معادلات واندروالس را بررسی میکنیم. معادله واندروالس را در ادامه اثبات میکنیم.
$$(\frac{\partial T}{\partial P})_ V = \frac { 1 } { (\frac{\partial P}{\partial T})_V }$$
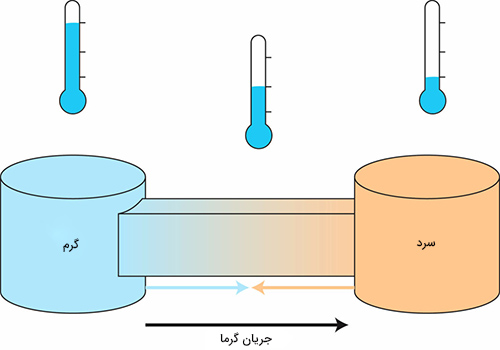
معادله واندروالس برحسب فشار به صورت زیر نوشته میشود:
$$P = \frac{RT}{V_ m - b} - \frac { a } { V_ m}$$
$$V_m$$ در رابطه فوق حجم مولی و برابر حجم سیستم تقسیم بر تعداد مولهای موجود در سیستم است. همانطور که در رابطه واندروالس دیده میشود، فشار تابعی از حجم و دما است، بنابراین مشتق فشار نسبت به دما، به صورت مشتق جزیی نوشته میشود. مشتق فشار نسبت به دما در حجم ثابت را بهدست میآوریم:
$$(\frac{\partial P}{\partial T})_V = \frac { R } { V_ m - b }$$
برای بهدست آوردن $$(\frac{\partial T}{\partial V}) _ V$$ معادله واندروالس را برحسب دما بهدست میآوریم:
$$P = \frac{RT}{V_ m - b} - \frac { a } { V_ m} \\ RT = P ( V _ m - b ) + \frac { a } { V _ m ^ 2 } ( V_ m - b) \\ T = \frac { P ( V _ m - b )} { R }+ \frac { a ( V _m - b ) } { R V _ m ^ 2 }$$
در ادامه، مشتق جزیی دما را نسبت به فشار در حجم ثابت بهدست میآوریم:
$$(\frac{\partial T}{\partial P})_ V = \frac{V_ m ^ 3 - b V _ m ^ 2}{R V _ m ^ 2}= \frac{V_m - b}{R}$$
با توجه به دو رابطه بهدست آمده $$(\frac{\partial P}{\partial T})_V = \frac { R } { V_ m - b }$$ و $$(\frac{\partial T}{\partial P})_ V = \frac{V_m - b}{R}$$ داریم:
$$(\frac{\partial T}{\partial P})_ V = \frac { 1 } { (\frac{\partial P}{\partial T})_V }$$
انتقال حرارت تحت حجم یا فشار ثابت
در این قسمت، با استفاده از قانون اول ترمودینامیک دو رابطه فیزیکی برای انتقال حرارت، $$q$$، بهدست میآوریم. در قسمتهای قبل گفتیم در قانون اول ترمودینامیک، انرژی درونی سیستم، گرما و کار با استفاده از رابطه زیر به یکدیگر مربوط میشوند:
$$\triangle U = q + w$$
به این نکته توجه داشته باشید که رابطه بالا صورت قانون اول ترمودینامیک در شیمی است. در فیزیک و مهندسی، قانون اول ترمودینامیک به صورت $$\triangle U = q - w$$ نوشته میشود. دو محیط متفاوت را در نظر میگیریم. کار انجام شده برای سیستمی مشخص به طور کامل به دلیل انبساط است. در این حالت، کار به صورت $$w = - \ P \triangle V$$ تعریف میشود. در این رابطه، $$P$$ فشار خارجی و $$\triangle V$$ تغییرات حجم سیستم پس از انجام کار است. این رابطه را در رابطه کلی قانون اول ترمودینامیک قرار میدهیم:
$$\triangle U = q - P \triangle V$$
حالت اول
در حالت اول، حجم را ثابت در نظر میگیریم. حجم ثابت به معنای ثابت ماندن حجم سیستم است، بنابراین تغییرات حجم برابر صفر خواهد بود:
$$\triangle V = 0$$
از اینرو، رابطه $$\triangle U = q - P \triangle V$$ به شکل $$\triangle U = q$$ در میآید:
$$q = \triangle U$$
در نتیجه، در حجم ثابت، گرمای وارد شده یا خارج شده از سیستم برابر تغییرات انرژی درونی سیستم است.
حالت دوم
در حالت دوم، فشار را ثابت در نظر میگیریم. این حالت در مقایسه با حالت اول رایجتر است. بار دیگر فرمول قانون اول ترمودینامیک را مینویسیم.
$$\triangle U = q - p \triangle V$$
عبارت $$p \triangle V$$ را به طرفین رابطه بالا اضافه میکنیم:
$$\triangle U + P \triangle V = q - P\triangle V + P \triangle V$$
رابطه فوق پس از سادهسازی به صورت زیر درمیآید:
$$\triangle U + P \triangle V = q$$
تابع دینامیکی جدیدی به نام $$\triangle H$$ را تعریف میکنیم:
$$\triangle H = \triangle U + P \triangle V$$
تغییرات انرژی درونی سیستم در قانون اول ترمودینامیک را جایگزین آن در رابطه مربوط به $$\triangle H$$ میکنیم:
$$\triangle H = q - P\triangle V + P \triangle V +\\ q = \triangle H$$
به این نکته توجه داشته باشید که $$H$$ همان آنتالپی است. بنابراین، هدایت گرمایی در فشار ثابت برابر تغییرات آنتالپی خواهد بود.
فرمول های ترمودینامیک در قانون دوم
در این بخش، قانون دوم ترمودینامیک را به صورت خلاصه توضیح میدهیم و در مورد روابط حاکم بر این قانون و اثبات ریاضی آنها صحبت میکنیم.
قانون دوم ترمودینامیک چیست ؟
در قانون دوم ترمودینامیک در مورد آنتروپی و رابطه آن با گرما صحبت میکنیم. میلهای فلزی را فرض کنید که بین دو جسم سرد و گرم قرار گرفته است.
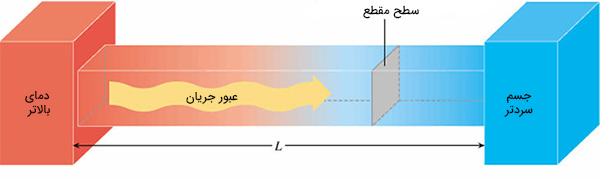
گرما به صورت طبیعی از جسم گرم به جسم سرد منتقل میشود. انتقال گرما از جسم گرم به جسم سرد فرایندی خودبهخودی است. بنابراین، گرما به صورت خودبهخودی از جسم سرد به گرم منتقل نخواهد شد. تنها راهی که از طریق آن گرما میتواند از جسم سرد به جسم گرم منتقل شود، تزریق انرژی به سیستم است. به عنوان مثال، در سیستم تبرید یخچال، انرژی گرمایی از مواد غذایی داخل یخچال گرفته و به بیرون از یخچال منتقل میشود. از اینرو، یخچال میتواند مواد غذایی داخل خود را سرد نگه دارد. این فرایند با گرفتن انرژی از خارج انجام میشود.
انتقال گرما از جسمی سرد به جسمی گرم، فرایندی خودبهخودی است. آنتروپی در فرایندهای خودبهخودی افزایش مییابد.
$$\triangle S > 0$$
به بیان دیگر، تغییرات آنتروپی در فرایندهای طبیعی بزرگتر از صفر است. تغییرات آنتروپی در فرایند برگشتپذیر ایدهال میتواند برابر صفر باشد. اما به این نکته توجه باشید که بیشتر سیستمهای ترمودینامیکی ایدهال نیستند، بنابراین آنتروپی فرایندهای طبیعی خودبهخودی افزایش مییابد. برای آنکه بدانیم چرا آنتروپی کاهش و افزایش مییابد، همیشه باید دو تغییر در آنتروپی را در نظر بگیریم:
- تغییر آنتروپی سیستم
- تغییر آنتروپی محیط اطراف سیستم
تغییر آنتروپی کیهان برابر مجموع تغییرات آنتروپی سیستم و محیط اطراف است:
$$\triangle S _ {univ} = \triangle S _ {sys} + \triangle S _ {surr} = \frac { q _ {sys}} { T } + \frac { q _{ surr} } { T}$$
در فرایند همدمای انبساطی برگشتپذیر، انرژی گرمایی جذب شده توسط سیستم از محیط اطراف برابر است با:
$$q _ {rev} = n R T \ln \frac { V_2} { V_1}$$
از آنجا که انرژی گرمایی جذب شده توسط سیستم برابر مقدار انرژی گرمایی از دست داده توسط محیط اطراف است:
$$q_sys_ = - \ q _ { surr}$$
بنابراین، برای فرایند برگشتپذیر کاملا ایدهآل، تغییرات آنتروپی برابر صفر خواهد بود:
$$\triangle S _ {univ} = \frac { n R T \ln \frac { V_2} { V_1}} { T} + \frac { - \ n R T \ln \frac { V_2} { V_1}} { T } = 0$$
اگر فرایند برگشتناپذیر باشد، تغییرات آنتروپی برابر است با:
$$\triangle S _ { univ} = \frac { n R T \ln \frac { V_2} { V_1} } { T } > 0$$
اگر دو معادله مربوط به تغییرات آنتروپی برای دو فرایند را در کنار یکدیگر قرار دهیم، به قانون دوم ترمودینامیک میرسیم:
$$\triangle S _ { univ } = \triangle S _ {sys} + \triangle S_ {surr} \geq 0$$
بازده کارنو
در این قسمت در مورد بازده موتور کارنو صحبت میکنیم. در حالت کلی، بازده موتور به صورت نسبت کار انجام شده توسط موتور به مقدار انرژی داده شده به آن تعریف میشود.
$$\eta= \frac { W } { Q }$$
بیشینه بازده موتورگرمایی که بین دو منبع با دماهای $$T_1$$ و $$T_2$$ قرار دارد برابر است با:
$$\eta = 1 - \frac { T_2 } { T _ 1 }$$
نامساوی کلاسیوس
همانطور که در مطالب بالا دیدیم آنتروپی به صورت زیر نوشته میشود:
$$dS= \frac { d q _ { rev}} { T }$$
در رابطه فوق:
- $$dq _ { rev}$$ مقدار گرمای منتقل شده در مسیر برگشتپذیر است.
- T دمای سیستم است.
گرما تابع حالت نیست. بر طبق چرخه کارنو، $$dq$$ در فرایند چرخهای مخالف صفر است. از اینرو، گرما تابعی از مسیر طی شده توسط سیستم خواهد بود. برای بهدست آوردن آنتروپی باید از طرفین رابطه $$dS= \frac { d q _ { rev}} { T }$$ انتگرال بگیریم. برای بهدست آوردن گرما و محاسبه انتگرال آن به مسیری برگشتپذیر نیاز داریم. نامساوی کلاسیوس به ما مقدار کمینهای را برای مسیر برگشتپذیر میدهد و آن را به قانون دوم ترمودینامیک مربوط میسازد. به بیان دیگر، این نامساوی مقدار کمینهای را برای دیگر مسیرها، به جز مسیر برگشتپذیر میدهد. قبل از اثبات این نامساوی به این نکته توجه داشته باشید که کار انجام شده در مسیر برگشتپذیر، بزرگتر از کار انجام شده در مسیر برگشتناپذیر است. منظور از کار انجام شده مقدار قدر مطلق آن (مقدار مثبت) است:
$$|dW_ {rev} | \geq |dW |$$
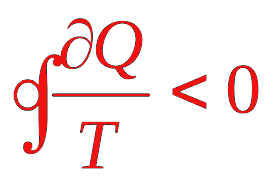
اگر سیستم کار انجام دهد، مقدار آن منفی خواهد بود. اگر قدر مطلق را از طرفین رابطه فوق برداریم، به نامساوی زیر میرسیم:
$$- \ dW_ {rev} \geq - \ dW $$
نامساوی فوق را به صورت زیر مینویسیم:
$$d W - d W_ { rev } \geq 0$$
اگر سیستم کار انجام دهد، مقدار - d W_ { rev } مثبت است. بنابراین، d W - d W_ { rev } همواره بزرگتر از صفر خواهد بود. برای اثبات نامساوی کلاسیوس از رابطه $$d W - d W_ { rev } \geq 0$$ استفاده میکنیم. برگشتپذیر بودن یا برگشتناپذیر بودن مسیر برای تابع حالت مهم نیست. همانطور که در مطالب بالا اشاره کردیم، انرژی درونی تابع حالت است. بر طبق قانون دوم ترمودینامیک، تغییرات انرژی درونی سیستم برابر است با:
$$d U = d q + d w$$
$$dq$$ و $$dw$$ گرمای منتقل شده و کار انجام شده در مسیر برگشتناپذیرِ تصادفی هستند. $$d q + d w$$ برابر گرمای منتقل شده و کار انجام شده در مسیر برگشتپذیر است:
$$d U = d q + d w = d q _ { rev } + d w _ {rev}$$
با توجه به رابطه فوق، تغییرات انرژی درونی در مسیر برگشتپذیر برابر تغییرات آن در مسیر برگشتناپذیر است. در رابطه $$ d q + d w = d q _ { rev } + d w _ {rev}$$، تغییرات گرما را در یک طرف تساوی و تغییرات در مقدار کار انجام شده را در طرف دیگر تساوی قرار میدهیم:
$$d w - d w _ { rev } = dq _ { rev } - dq$$
تفاضل $$d w - d w _ { rev }$$ شما را به یاد چه رابطهای میاندازد؟ در ابتدای این بخش نامساوی زیر را بهدست آوردیم:
$$d W - d W_ { rev } \geq 0$$
بنابراین، $$ dq _ { rev } - dq$$ مساوی یا بزرگتر از صفر خواهد بود:
$$ dq _ { rev } - dq \geq 0$$
نامساوی فوق را به صورت زیر مینویسیم:
$$dq _ { rev } \geq d q $$
بر طبق رابطه بالا، گرمای منتقل شده در فرایند برگشتپذیر، همواره برابر یا بزرگتر از گرمای منتقل شده در فرایند برگشتناپذیر است. طرفین نامساوی $$dq _ { rev } \geq d q $$ را بر دما تقسیم میکنیم. از آنجا که دما همواره مثبت است، جهت نامساوی تغییری نخواهد کرد:
$$\frac { d q _ { rev } } { T } \geq \frac { d q } { T }$$
در ابتدای این بخش گفتیم $$\frac { d q _ { rev } } { T } $$ برابر تغییرات آنتروپی است. در نتیجه داریم:
$$d S \geq \frac { d q } { T }$$
این نامساوی، نامساوی کلاسیوس نام دارد. آنتروپی در فرایند برگشتپذیر برابر نسبت گرمای منتقل شده به دما است. مقدار آنتروپی در هر فرایند برگشتناپذیری مساوی یا بزرگتر از نسبت گرمای منتقل شده به دما است.
همانطور که در مطالب بالا گفتیم تغییرات آنتروپی را میتوانیم به صورت زیر نوشت:
$$\triangle S _ { total} = \triangle S _ { univ } = \triangle S _ {sys} + \triangle S_ {surr} $$
تغییرات آنتروپی محیط اطراف برابر تغییرات آنتالپی تقسیم بر دما است:
$$\triangle S _ {surr} = \frac { \triangle H _ {sys} } { T }$$
رابطه بالا را در فرمول $$\triangle S _ { univ } = \triangle S _ {sys} + \triangle S_ {surr}$$ قرار میدهیم. سپس طرفین آن را در $$T$$ و ۱- ضرب میکنیم. پس از سادهسازی به رابطه زیر میرسیم:
$$- \ T \triangle S_ { univ} = \triangle H _ {Sys} - T \triangle S _ {sys
} $$
سمت چپ رابطه بالا را برابر $$\triangle G$$، تغییرات انرژی آزاد گیبس، قرار میدهیم:
$$\triangle G = \triangle H - T \triangle S$$
اثبات فرمول بنیادی ترمودینامیک با استفاده از قانون های اول و دوم ترمودینامیک
در این بخش، قانون بنیادی ترمودینامیک که ترکیبی از قانونهای اول و دوم ترمودینامیک است را بهدست میآوریم. رابطه قانون اول ترمودینامیک به شکل دیفرانسیلی به صورت زیر نوشته میشود:
$$d U = dq + d w$$
تغییرات گرما در فرایند برگشتپذیر به صورت زیر نوشته میشود:
$$d q _ { rev } = T dS$$
همچنین، تغییرات کار در فرایند برگشتپذیر برابر است با:
$$d w = - \ P d V$$
به این نکته توجه داشته باشید که فرمول کار را تنها برای حالت انبساط نوشتهایم. با ترکیب سه رابطه فوق با یکدیگر داریم:
$$d U = T d S - P d V$$
تغییرات کار و گرما را برای فرایندهای برگشتپذیر نوشتیم. اما به این نکته توجه داشته باشید که انرژی درونی تابع حالت و مستقل از مسیر طی شده توسط سیستم است. در نتیجه، رابطه فوق نهتنها برای فرایندهای برگشتپذیر، بلکه برای تمام فرایندها صحیح است. فرمول $$d U = T d S - P d V$$ یکی از بنیادیترین و مهمترین فرمول های ترمودینامیک است، زیرا قانون اول و دوم ترمودینامیک در این فرمول با یکدیگر ترکیب شدهاند. همانطور که در این رابطه بنیادی میبینیم، $$dU$$ تابعی از تغییرات آنتروپی و حجم است. بنابراین، انرژی درونی را میتوانیم به صورت تابعی از آنتروپی و حجم تعریف کنیم:
$$U= U ( S , V)$$
در نتیجه، $$ dU$$ را می توانیم به صورت زیر نیز بنویسیم:
$$dU= (\frac{\partial U}{\partial S})_ V \ d S + (\frac{\partial U}{\partial V})_ S \ dV$$
با مقایسه رابطه بالا با رابطه $$d U = T d S - P d V$$ داریم:
$$(\frac{\partial U}{\partial S})_ V = T \\ (\frac{\partial U}{\partial V})_ S = - \ P$$
همانطور که در مطالب بالا اشاره کردیم انرژی آزاد گیبس، تابع حالت و کمیت بسیار مهمی در قانون دوم ترمودینامیک است. برای آنکه $$dG$$، تغییرات انرژی آزاد گیبس برای فرایند خودبهخودی کوچکتر از صفر باشد، قانون دوم ترمودینامیک باید مجدد به صورت دیگری نوشته شود. در مطالب بالا قانون اول و دوم ترمودینامیک را با یکدیگر ترکیب کردیم و فرمول بنیادی برای انرژی درونی سیستم بهدست آوردیم. در ادامه این بخش، کار مشابهی را برای انرژی آزاد گیبس انجام میدهیم. انرژی آزاد گیبس را به صورت زیر تعریف کردیم:
$$G = H - TS$$
از طرفین رابطه فوق مشتق میگیریم:
$$dG = dH - T dS - S dT$$
آنتالپی با استفاده از رابطه زیر بهدست میآید:
$$H = + PV$$
به طور مشابه، از طرفین رابطه فوق نیز مشتق میگیریم:
$$dH = dU + P dV + V d P$$
رابطه بهدست آمده برای $$dH$$ را در رابطه $$dG$$ قرار میدهیم:
$$dG = ( d U + P d V + V d P ) - TdS - SdT$$
در ابتدای بخش تغییرات انرژی درونی را به صورت $$dU = TdS - PdV$$ بهدست آوردیم. $$dU$$ را در رابطه $$dG$$ قرار میدهیم:
$$dG = TdS - PdV + pdV + V d P - T dS - SdT$$
پس از سادهسازی فرمول فوق، رابطه زیر برای $$dG$$ بهدست میآید:
$$dG = V d P - S d T$$
با نگاهی به رابطه بهدست آمده برای تغییرات انرژی آزاد گیبس میتوانیم G را به صورت تابعی از دو کمیت فشار و دما تعریف کنیم:
$$G = G ( P , T)$$
در نتیجه، $$ dG $$ را می توانیم به صورت زیر نیز بنویسیم:
$$dG = (\frac{\partial G}{\partial P})_ T \ d P + (\frac{\partial G}{\partial T}) _ P \ d T$$
به دو رابطه بهدست آمده برای $$ dG $$ دقت کنید:
$$dG = (\frac{\partial G}{\partial P})_ T \ d P + (\frac{\partial G}{\partial T}) _ P \ d T \\ d G = V d P - S dT$$
ضریبهای $$dP$$ و $$d T$$ در دو رابطه را میتوانیم با یکدیگر مقایسه کنیم:
$$V = (\frac{\partial G}{\partial P})_ T \\ S = -\ (\frac{\partial G}{\partial T}) _ P $$
اثبات روابط ماکسول با استفاده از U و H
فرمول های ترمودینامیکی ماکسول توسط فیزیکدانی اسکاتلندی با همین نام بهدست آمدند. دلیل شهرت ماکسول نه به خاطر معادلات ماکسول در ترمودینامیک، بلکه به خاطر معادلات مشهور ماکسول در الکترومغناطیس است. فرض کنید رابطهای به شکل زیر داریم:
$$M d x + N dy$$

M و N در رابطه فوق هر دو تابعی از $$x$$ و $$y$$ هستند. رابطه فوق در صورتی دیفرانسیل کامل است اگر:
$$(\frac{\partial M}{\partial y})_x = (\frac{\partial N}{\partial x})_y $$
اگر رابطه بالا برقرار باشد، عبارت $$M d x + N dy$$ دیفرانسیل کامل است. اگر تساوی فوق برقرار نباشد، عبارت $$M d x + N dy$$ دیفرانسیل کامل نیست. همانطور که در مطالب بالا دیدیم دیفرانسیل کامل انرژی درونی، $$dU$$، را میتوانیم به صورت زیر بنویسیم:
$$d U = T d S - P dV $$
با توجه به رابطه بالا، انرژی درونی تابع حالتی از دو کمیت آنتروپی و حجم است . دیفرانسیل کامل آن را میتوان به صورت زیر نیز نوشت:
$$dU = (\frac{\partial U}{\partial S})_T \ dS + (\frac{\partial U}{\partial V} ) _ S \ dS$$
با برابر قرار دادن سمت راست دو معادله فوق به دو رابطه زیر میرسیم:
$$(\frac{\partial U}{\partial S}) _ V = T \\ (\frac{\partial U}{\partial V}) _ S = - \ P $$
دو رابطه فوق را در بخش قبل بهدست آوردیم. در ادامه، با استفاده از تساوی $$(\frac{\partial M}{\partial y})_x = (\frac{\partial N}{\partial x})_y $$، فرمولهای بیشتری را بهدست میآوریم. از آنجا که انرژی درونی تابع حالت است، عبارت $$TdS - P dV$$ دیفرانسیل کامل خواهد بود. بنابراین:
$$(\frac{\partial P}{\partial S})_ S = - \ (\frac{\partial P}{\partial S}) _ V$$
رابطه فوق، نخسین رابطه ماکسول است. بنابراین، برای بهدست آوردن نخستین رابطه ماکسول از رابطه $$dU$$ برحسب $$dS$$ و $$dV$$ استفاده میکنیم. برای بهدست آوردن رابطه دوم ماکسول از فرمول آنتالپی استفاده میکنیم. آنتالپی را به صورت زیر تعریف کردیم:
$$H = U + PV$$
دیفرانسیل H به صورت زیر نوشته میشود:
$$d H = dU + PdV + V dP$$
در ادامه، به جای $$dU$$ در رابطه فوق، عبارت $$TdS - P dV$$ را قرار میدهیم:
$$dH = TdS - P dV + PdV + V dP$$
عبارت $$P dV$$ با $$- \ Pd V$$ ساده میشود. در نتیجه، $$dH$$ به صورت زیر نوشته میشود:
$$dH = T d S + V d P$$
از آنجا که آنتالپی تابع حالت است، دیفرانسیل کامل آن را میتوانیم به صورت زیر بنویسیم:
$$dH = (\frac{\partial H}{\partial S})_ P \ dS + (\frac{\partial H}{\partial P})_ S \ dP$$
با برابر قرار دادن سمت راست دو معادله فوق به دو رابطه زیر میرسیم:
$$(\frac{\partial H}{\partial S}) _ P = T \\ (\frac{\partial H}{\partial P}) _ S = V$$
دو رابطه فوق را در بخش قبل بهدست آوردیم. در ادامه، با استفاده از تساوی $$(\frac{\partial M}{\partial y})_x = (\frac{\partial N}{\partial x})_y $$، فرمولهای بیشتری را بهدست میآوریم. از آنجا که آنتالپی تابع حالت است، عبارت $$TdS + V dP$$ دیفرانسیل کامل خواهد بود. بنابراین:
$$(\frac{\partial T}{\partial P})_ S = \ (\frac{\partial V}{\partial S}) _ P$$
رابطه فوق، دومین رابطه ماکسول است. برای بهدست آوردن دومین رابطه ماکسول از رابطه آنتالپی استفاده میکنیم.
اثبات روابط ماکسول با استفاده از A و G
در این بخش، دو رابطه باقیمانده از روابط ماکسول را با استفاده از انرژی آزاد گیبس و انرژی آزاد هلمهولتز بهدست میآوریم. ابتدا از انرژی آزاد هلمهولتز، $$A$$، استفاده میکنیم. $$A$$ از کلمه آلمانی arbeiten به معنای کار گرفته شده است. در شرایطِ حجم ثابت، انرژی آزاد هلمهولتز بیشینه مقدار کار را به ما میدهد. این انرژی به صورت زیر تعریف میشود:
$$A = U - TS$$
دیفرانسیل $$dA$$ برابر است با:
$$d A = d U - T dS - S dT$$
همانطور که در بخشهای قبل گفتیم، $$dU$$ با استفاده از ترکیب قانونهای اول و دوم ترمودینامیک به صورت زیر نوشته میشود:
$$dU = T d S - P d V$$
رابطه فوق برای $$d U$$ را در رابطه $$d A = d U - T dS - S dT$$ قرار میدهیم:
$$d A = ( T dS - P d V ) - TdS - SdT$$
با ساده کردن عبارتهای $$T d S$$ و $$- \ T d S$$ با یکدیگر، $$dA$$ به صورت زیر نوشته میشود:
$$d A = - P d V - S d T$$
انرژی آزاد هلمهولتز نیز تابع حالت است. بنابراین، دیفرانسیل کامل این تابع را میتوانیم به صورت زیر نیز بنویسیم:
$$dA = (\frac{\partial A}{\partial V})_ T \ d V + (\frac{\partial A}{\partial T})_V \ d T$$
با برابر قرار دادن سمت راست دو معادله فوق به دو رابطه زیر میرسیم:
$$(\frac{\partial A}{\partial V}) _ T = - \ P \\ (\frac{\partial A}{\partial T}) _ V = - \ S$$
در ادامه، با استفاده از تساوی $$(\frac{\partial M}{\partial y})_x = (\frac{\partial N}{\partial x})_y $$، فرمولهای بیشتری را بهدست میآوریم. از آنجا که انرژی آزاد هلمهولتز تابع حالت است، عبارت $$- P d V - S d T$$ دیفرانسیل کامل خواهد بود. بنابراین:
$$- \ (\frac{\partial P}{\partial T})_ V = \ (\frac{\partial S}{\partial V}) _ T$$
رابطه چهارم ماکسول را با استفاده از انرژی آزاد گیبس بهدست میآوریم. G به صورت زیر نوشته میشود:
$$G = H - TS$$
با توجه به رابطههای انرژی آزاد هلمهولتز و انرژی آزاد گیبس متوجه میشویم که این دو کمیت توسط انرژی درونی و آنتالپی به یکدیگر مربوط میشوند. در بخش قبل $$dG$$ را به صورت زیر نوشتیم:
$$dG = V d P - S dT$$
از آنجا که انرژی آزاد گیبس تابع حالت است، آن را میتوانیم به صورت دیفرانسیل کامل بنویسیم:
$$dG = (\frac{\partial G}{\partial P})_ T \ d P + (\frac{\partial G}{\partial T})_ P \ d T$$
دو رابطه بهدست آمده برای $$dG$$ را برابر یکدیگر قرار میدهیم. برای آنکه تساوی برقرار باشد، باید ضریبهای $$dP$$ و $$dT$$ با یکدیگر برابر باشند:
$$V = (\frac{\partial G}{\partial P}) _ T \\ - \ S = (\frac{\partial G}{\partial T})_ P$$
G تابع حالت است، بنابراین دیفرانسیل آن، دیفرانسیل کامل خواهد بود.. در نتیجه:
$$- \ (\frac{\partial V}{\partial T})_ P = - \ (\frac{\partial S}{\partial P}) _ T$$
رابطه فوق چهارمین و آخرین رابطه ماکسول است. روابط ماکسول در جدول زیر به صورت خلاصه نوشته شدهاند:
| رابطههای ماکسول | فرمول | شروع از رابطه |
| رابطه اول ماکسول | $$(\frac{\partial P}{\partial S})_ S = - \ (\frac{\partial P}{\partial S}) _ V$$ | $$d U = T d S - P dV $$ |
| رابطه دوم ماکسول | $$(\frac{\partial T}{\partial P})_ S = \ (\frac{\partial V}{\partial S}) _ P$$ | $$H = U + PV$$ |
| رابطه سوم ماکسول | $$- \ (\frac{\partial P}{\partial T})_ V = \ (\frac{\partial S}{\partial V}) _ T$$ | $$A = U - TS$$ |
| رابطه چهارم ماکسول | $$- \ (\frac{\partial V}{\partial T})_ P = - \ (\frac{\partial S}{\partial P}) _ T$$ | $$G = H - TS$$ |
تا اینجا با بنیادیترین فرمول های ترمودینامیکی مانند رابطه $$d U = T d S - P dV $$ و روابط ماکسول آشنا شدیم و آنها را اثبات کردیم. در ادامه، تغییرات آنتروپی نسبت به حجم را بهدست میآوریم.
تغییرات آنتروپی نسبت به حجم
در مطالب بالا در مورد گاز ایدهال و گاز واندروالس و فرمول های ترمودینامیک حاکم بر آنها صحبت کردیم. در این بخش، تغییرات آنتروپی نسبت به حجم را برای گاز واندروالس بهدست میآوریم و ان را با گاز ایدهال مقایسه میکنیم. به بیان دیگر، $$( \frac{\partial S}{\partial V})_ T$$ را برای گاز واندروالس بهدست میآوریم. رابطه واندروالس را به صورت زیر بهدست آوردیم:
$$P = \frac { R T } { V _ m - b } - \frac { a } { V _ m ^ 2 } $$
در رابطه فوق، $$V_m$$ برابر حجم مولی و نسبت حجم به تعداد مولها، n، است:
$$V_m = \frac { V } { n }$$
n و $$V$$ در رابطه فوق مقادیر فزونور یا مقداری هستند و به اندازه سیستم بستگی دارند، اما $$V_m$$، کمیتی نافزونور یا شدتی است و به بزرگی سیستم وابسته نیست. با توجه به معادله واندروالس، محاسبه $$( \frac{\partial S}{\partial V})_ T$$ بسیارسخت به نظر میرسد، زیرا آنتروپی در رابطه واندروالس وجود ندارد. با استفاده از یکی از معادلههای ماکسول انجام این کار بسیار راحت میشود.
$$( \frac{\partial S}{\partial V})_ T = (\frac{\partial P}{\partial T})_V$$
در نتیجه، برای بهدست آوردن تغییرات آنتروپی نسبت به حجم در دمای ثابت، تنها کافی است تغییرات فشار نسبت به دما را در حجم ثابت بهدست آوریم.
$$ (\frac{\partial P}{\partial T})_V = (\frac{\partial (\frac { R T } { V _ m - b } - \frac { a } { V _ m ^ 2 })}{\partial T})_V = \frac { R } { V _ m -b }$$
با توجه به تساوی $$( \frac{\partial S}{\partial V})_ T = (\frac{\partial P}{\partial T})_V$$، تغییرات آنتروپی نسبت به حجم در دمای ثابت برابر است با:
$$ (\frac{\partial S}{\partial V})_T = \frac { R } { V _ m -b }$$
در ادامه، $$(\frac{\partial S}{\partial V})_T$$ را برای گاز ایدهال بهدست میآوریم. معادله حالت برای گاز ایدهال به صورت زیر نوشته میشود:
$$P = \frac { RT } { V _ m }$$
تغییرات آنتروپی نسبت به حجم در دمای ثابت را به صورت مشابه بهدست میآوریم. برای این کار کافی است تغییرات فشار نسبت به دما در حجم ثابت را محاسبه کنیم.
$$ (\frac{\partial S}{\partial V})_T = \frac { R } { V _ m }$$
سوال مهمی که ممکن است مطرح آن است که افزایش آنتروپی با افزایش حجم برای کدام گاز سریعتر رخ میدهد. برای پاسخ به این پرسش تغییرات آنتروپی نسبت به حجم را با یکدیگر مقایسه میکنیم:
$$ (\frac{\partial S}{\partial V})_T = \frac { R } { V _ m -b }$$
$$ (\frac{\partial S}{\partial V})_T = \frac { R } { V _ m }$$
در مطالب بالا به این موضوع اشاره کردیم که مولکولهای تشکیلدهنده گاز حجم مشخصی را اشغال میکنند، بنابراین از ضریب b برای اصلاح حجم استفاده کردیم. از اینرو، مقدار b برای هر گاز واندروالسی مثبت و بزرگتر از صفر خواهد بود. در این صورت، $$V_m -b$$ کوچکتر از $$V_m$$ و بنابراین، $$\frac { R } { V _ m - b}$$ بزرگتر از $$\frac { R } { V _ m }$$ است. در نتیجه، تغییرات آنتروپی نسبت به حجم در دمای ثابت برای گاز واندروالس بزرگتر از گاز ایدهال خواهد بود.
تغییرات آنتالپی نسبت به فشار در دمای ثابت
برای بهدست آوردن تغییرات آنتالپی نسبت به فشار در دمای ثابت از رابطه زیر استفاده میکنیم:
$$(\frac{\partial f}{\partial x})_z = (\frac{\partial f}{\partial x})_y + (\frac{\partial f}{\partial y})_x (\frac{\partial y}{\partial x})_z$$
در رابطه فوق f را با H (آنتالپی)، $$x$$ را با فشار، $$y$$ را با آنتروپی و $$z$$ را با دما جایگزین میکنیم. بنابراین، معادله فوق به شکل زیر نوشته میشود:
$$(\frac{\partial H}{\partial P})_T = (\frac{\partial H}{\partial P})_S + (\frac{\partial H}{\partial S})_P (\frac{\partial S}{\partial P})_T$$
رابطه ۱
با توجه به معادلات ماکسول، تغییرات آنتروپی نسبت به فشار در دمای ثابت برابر منفی تغییرات حجم نسبت به دما در فشار ثابت است:
$$(\frac{\partial S}{\partial P})_T = - \ (\frac{\partial V}{\partial T})_P $$
رابطه ۲
رابطه ۲ را در رابطه یک قرار میدهیم:
$$(\frac{\partial H}{\partial P})_T = (\frac{\partial H}{\partial P})_S - (\frac{\partial H}{\partial S})_P (\frac{\partial V}{\partial T})_P
$$
رابطه ۳
در بخشهای قبل نشان دادیم که تغییرات آنتالپی نسبت به آنتروپی در فشار ثابت برابر دما است. در نتیجه، رابطه ۳ به شکل زیر نوشته میشود:
$$(\frac{\partial H}{\partial P})_T = (\frac{\partial H}{\partial P})_S - T (\frac{\partial V}{\partial T})_P
$$
همچنین، نشان دادیم تغییرات آنتالپی نسبت به فشار در آنتروپی ثابت برابر حجم است. از اینرو، رابطه فوق را به صورت زیر مینویسیم:
$$(\frac{\partial H}{\partial P})_T = V - T (\frac{\partial V}{\partial T})_P
$$
در ادامه، تغییرات آنتالپی نسبت به فشار در دمای ثابت را برای گاز ایدهال بهدست میآوریم. رابطه بین فشار، حجم و دما برای گاز ایدهال به صورت زیر نوشته میشود:
$$P = \frac { n \ R \ T } { V } $$
رابطه فوق را بر حسب فشار مرتب میکنیم:
$$V = \frac { n \ R \ T } { P } $$
سپس، تغییرات حجم نسبت به دما در فشار ثابت را محاسبه میکنیم:
$$(\frac{\partial V}{\partial T}) _ P = (\frac{\partial (\frac { n \ R \ T } { P })}{\partial T}) _ P = \frac { n R } { P }$$
بنابراین، تغییرات آنتالپی نسبت به فشار در دمای ثابت برای گاز ایدهال به صورت زیر نوشته میشود:
$$(\frac{\partial H}{\partial P})_T = \frac { n R T } { P } - T \times
\frac { nR } { P } = \frac { n R T } { P } - \frac { n R T } { P } = 0$$
با توجه به رابطه فوق، تغییرات آنتالپی نسبت به فشار در دمای ثابت برای گاز ایدهال برابر صفر است. این بدان معنا است که در گاز ایدهال اگر دما را ثابت نگه داریم و فشار را تغییر دهیم، مقدار آنتالپی ثابت باقی خواهد ماند. در ادامه این بخش، تغییرات آنتالپی نسبت به فشار در دمای ثابت را برای گاز بدون برهمکنش واندروالسی بهدست میآوریم. در حالت کلی معادله واندروالس به صورت زیر نوشته می شود:
$$P = \frac { R T } { V _ m - b } - \frac { a } { V _ m ^ 2 } $$
از آنجا که گاز واندروالس را بدون برهمکنش در نظر گرفتهایم، عبارت $$\frac { a } { V _ m ^ 2 }$$ از معادله فوق حذف خواهد شد.
$$P = \frac { R T } { V _ m - b }$$
برای بهدست آوردن تغییرات آنتروپی نسبت به فشار، رابطه نوشته شده برای فشار را برحسب حجم مرتب میکنیم:
$$V_ m = \frac { RT } { P } + b$$
از آنجا که $$V_m$$ برابر $$\frac { V } { n }$$ است:
$$V_ m = \frac { RT } { P } + b \\ \frac { V } { n} = \frac { RT } { P} + b \\ V = \frac { v R T } { P} + nb$$
در نتیجه، تغییرات حجم نسبت به دما در فشار ثابت برابر است با:
$$(\frac{\partial V}{\partial T})_ P = \frac { n R } { T }$$
در نتیجه، تغییرات آنتالپی نسبت به فشار در دمای ثابت برای گاز غیر برهمکنشی واندروالس برابر است با:
$$(\frac{\partial H}{\partial P})_ T = V - T (\frac{\partial V}{\partial T})_ P \\ (\frac{\partial H}{\partial P})_ T = \frac { n R T } { P } + nb - \frac { n R T } { P } = n b$$
بنابراین، تغییرات آنتالپی نسبت به فشار در دمای ثابت برای گاز واندروالس بدون برهمکنش برابر صفر است.
تا اینجا با برخی از مهمترین فرمول های ترمودینامیک آشنا شدیم. در ادامه، فرمول ظرفیت گرمایی در حجم ثابت را بهدست میآوریم.
فرمول ظرفیت گرمایی در حجم ثابت
ظرفیت گرمایی در حجم ثابت با استفاده از رابطه زیر بهدست میآید:
$$C_V = - \ (\frac{\partial U }{\partial V} ) _ T (\frac{\partial V}{\partial T})_ U$$
به رابطه فوق دقت کنید. چه چیزی در این رابطه توجه شما را به خود جلب میکند؟ هر دو مشتق جزیی در رابطه بالا از متغیرهای یکسانی تشکیل شدهاند.
- انرژی درونی
- حجم
- دما
به همین دلیل میتوانیم از جایگشت چرخهای استفاده کنیم.
$$ (\frac{\partial U }{\partial T} ) _ V \ (\frac{\partial T}{\partial V})_ U \ (\frac{\partial V}{\partial U})_ T = -1$$
رابطه فوق با استفاده از ویژگی مشتق جزیی اثبات میشود. به دو رابطه $$ (\frac{\partial U }{\partial T} ) _ V \ (\frac{\partial T}{\partial V})_ U \ (\frac{\partial V}{\partial U})_ T = -1$$ و C_V = - \ (\frac{\partial U }{\partial V} ) _ T (\frac{\partial V}{\partial T})_ U دقت کنید. $$ (\frac{\partial U }{\partial V} ) _ T$$ در رابطه ظرفیت گرمایی عکس رابطه $$(\frac{\partial V}{\partial U})_ T$$ در جاگشت چرخهای است. طرفین رابطه جایگشت چرخهای را در $$ (\frac{\partial U }{\partial V} ) _ T$$ ضرب میکنیم:
$$ (\frac{\partial U }{\partial T} ) _ V \ (\frac{\partial T}{\partial V})_ U \ = - \ (\frac{\partial U}{\partial V})_ T$$
همچنین، رابطههای $$ (\frac{\partial V}{\partial T})_ U$$ در ظرفیت گرمایی و $$(\frac{\partial T}{\partial V})_ U$$ در جایگشت چرخهای نیز عکس یکدیگر هستند. برای رسیدن به رابطه ظرفیت گرمایی در حجم ثابت، طرفین رابطه $$ (\frac{\partial U }{\partial T} ) _ V \ (\frac{\partial T}{\partial V})_ U \ = - \ (\frac{\partial U}{\partial V})_ T$$ را در $$ (\frac{\partial V}{\partial T})_ U$$ ضرب میکنیم:
$$ (\frac{\partial U }{\partial T} ) _ V = - \ (\frac{\partial U}{\partial V})_ T \ (\frac{\partial V}{\partial T})_ U \$$
سمت راست رابطه ظرفیت گرمایی در حجم ثابت را اثبات کردیم. برای رسیدن به سمت چپ معادله، یعنی ظرفیت گرمایی در حجم ثابت، باید تعریف ترمودینامیکی آن را بدانیم. ظرفیت گرمایی در حجم ثابت به صورت مشتق جزیی انرژی درونی نسبت به دما در حجم ثابت تعریف میشود:
$$C_V = (\frac{\partial U }{\partial T} ) _ V$$
در نتیجه، ظرفیت گرمایی در حجم ثابت برابر است با:
$$ C _ V = - \ (\frac{\partial U}{\partial V})_ T \ (\frac{\partial V}{\partial T})_ U \$$
تغییرات انرژی گیبس نسبت به فشار
در قسمتهای قبل با برخی از فرمول های ترمودینامیک آشنا شدیم. در این قسمت، تغییرات انرژی آزاد گیبس نسبت به فشار را بهدست میآوریم. تغییرات انرژی گیبس با استفاده از رابطه زیر نوشته میشود:
$$dG = - \ S d T + V d P$$
اگر تغییرات دما برابر صفر باشد، رابطه فوق به صورت زیر نوشته میشود:
$$dG = V dP$$
فرض کنید فشار سیستم از مقدار $$P_1$$ به $$P_2$$ تغییر میکند. با گرفتن انتگرال از طرفین رابطه $$dG = V dP$$ داریم:
$$\int_{ P_ 1}^{ P _ 2} d G = \int_{P_ 1}^{ P _ 2} V d P$$
فرض کنید سیستم از گاز ایدهال تشکیل شده باشد، بنابراین حجم به صورت زیر نوشته میشود:
$$V = \ frac { n R T } { P }$$
با قرار دادن ٰرابطه فوق در انتگرال داریم:
$$\int_{ P_ 1}^{ P _ 2} d G = \int_{P_ 1}^{ P _ 2} \ frac { n R T } { P } d P$$
با توجه به آنکه تغییرات دما را برابر صفر در نظر گرفتیم، تنها متغیر در رابطه $$\frac { n R T } { P }$$، فشار است. از اینرو انتگرال به صورت زیر مینویسیم:
$$\int_{ P_ 1}^{ P _ 2} d G =n R T \int_{P_ 1}^{ P _ 2} \ frac { d P} { P }$$
انتگرال $$int_{ P_ 1}^{ P _ 2} d G$$ برابر $$G ( P _ 2 ) - G ( P _1 ) $$ است. بنابراین، داریم:
$$G ( P_ 2 ) - G ( P _ 1 ) = n R T \int_{P_ 1}^{ P _ 2} \frac { d P } { P }$$
انتگرال $$\int_{P_ 1}^{ P _ 2} \frac { d P } { P }$$ برابر $$\ln \frac { P _ 1 } { P _ 1 }$$ است:
$$G ( P_ 2 ) - G ( P _ 1 ) = n R T \ln \frac { P _ 1 } { P _ 1 }$$
رابطه فوق را برحسب $$G ( P _ 2 )$$ مرتب میکنیم:
$$G ( P_ 2 ) = G ( P _ 1 ) + n R T \ln \frac { P _ 1 } { P _ 1 }$$
اثبات معادله گیبس-هلمهولتز و قانون دوم ترمودینامیک
در این بخش، رابطه بین تغییرات انرژی آزاد گیبس و قانون دوم ترمودینامیک را بررسی میکنیم. در مطالب بالا گفتیم بر طبق قانون دوم ترمودینامیک، تغییرات آنتروپی کیهان در فرایند خودبهخودی بزرگتر از صفر است. اما تغییرات انرژی آزاد گیبس در فرایند خودبهخودی کمتر از صفر است. آیا منفی بودن تغییرات انرژی آزاد گیبس برای فرایند خودبهخودی، قانون دوم ترمودینامیک را نقض میکند؟ سوال مهم دیگری که ممکن است مطرح شود آن است که چرا تابع جدیدی به نام انرژی آزاد گیبس را تعریف میکنیم. نکته مهمی که باید به آن توجه داشته باشیم، کلمه کیهان یا جهان است. جهان را میتوان به دو بخش تقسیم کرد:
- سیستم
- محیط اطراف
این تقسیمبندی در قانون دوم ترمودینامیک از اهمیت ویژهای برخوردار است. در بخشهای قبل تغییرات انرژی آزاد گیبس را به صورت زیر تعریف کردیم:
$$\triangle G = \triangle H - T \triangle S$$
در رابطه فوق، $$\triangle H$$، تغییرات آنتالپی، T دما و $$\triangle S$$ تغییرات آنتروپی هستند. به این نکته توجه داشته باشید که توابعی مانند انرژی آزاد گیبس یا آنتالپی برای آن اختراع شدند که توجه اصلی ما روی سیستم و نه محیط اطراف آن است. از اینرو، تغییرات منفی انرژی آزاد گیس در فرایندهای خودبهخودی در تضاد با قانون دوم ترمودینامیک نیست، زیرا تغییرات آنتروپی برای تمام کیهان در نظر گرفته میشود، اما تغییرات انرژی آزاد گیبس را تنها برای سیستم در نظر میگیریم. به بیان دیگر، مثبت بودن تغییرات آنتروپی کیهان و منفی بودن تغییرات انرژی آزاد گیبس در فرایندهای خودبهخودی مفهوم یکسانی را بیان میکنند. دو رابطه زیر را در نظر بگیرید:
$$\triangle G _ { sys } < 0 \\ \triangle G _ { sys } = \triangle H _ { sys } - T \triangle S _ { sys }$$
در نتیجه داریم:
$$ \triangle H _ { sys } - T \triangle S _ { sys } < 0$$
در نخستین گام، طرفین رابطه بالا را در ۱- ضرب میکنیم:
$$T \triangle _ { sys } - \triangle G _ { sys } > 0 $$
در گام دوم، طرفین نامساوی فوق را بر T تقسیم میکنیم:
$$\frac { T \triangle S_ { sys }} { T }- \frac {\triangle G _ { sys }} { T } > \frac { 0 } { T }$$
به این نکته توجه داشته باشید که دما (برحسب کلوین) در ترمودینامیک همواره مثبت است. با ساده کردن نامساوی فوق داریم:
$$\triangle S_ { sys } - \frac { \triangle H _ { sys } } { T } > 0$$
تغییرات آنتروپی محیط اطراف به صورت زیر تعریف میشود:
$$\triangle S_ { surr } = - \ \frac { \triangle H _ { sys } } { T }$$
بنابراین، در رابطه $$\triangle S_ { sys } - \frac { \triangle H _ { sys } } { T } > 0$$ به جای $$\frac { \triangle H _ { sys } } { T } $$ تغییرات آنتروپی محیط اطراف را قرار میدهیم:
$$\triangle S _ { sys } + \triangle S _ { surr } > 0 $$
سیستم و محیط اطراف با یکدیگر، جهان یا کیهان را تشکیل میدهند:
$$\triangle S _ { universe } > 0 $$
از اینرو، تغییرات آنتروپی کیهان در فرایندهای خودبهخودی بزرگتر از صفر است. بنابراین، منفی بودن تغییرات انرژی آزاد گیبس برای فرایندهای خودبهخودی همان بیان دیگر قانون دوم ترمودینامیک است.
تغییرات آنتروپی و حجم نسبت به دما و فشار
برای هر ماده سادهای رابطهای بین حجم، دما و فشار وجود دارد که به صورت زیر نوشته میشود:
$$V = V ( T , P)$$
از آنجا که حجم، دما و فشار همگی توابع حالت هستند، تغییرات حجم را میتوانیم به صورت زیر بنویسیم:
$$d V = M d T + N d P$$
ضرایب M و N در رابطه فوق به صورت زیر نوشته میشوند:
$$dV = (\frac{\partial V}{\partial P} ) _ P \ d T + (\frac{\partial V}{\partial P} ) _ T \ d P $$
مشتقهای جزیی در رابطه $$dV$$ را میتوانیم برحسب متغیرهای تجربی $$\alpha$$ و $$\beta$$ به صورت زیر بنویسیم:
$$\alpha = \frac { 1 } { V} (\frac{\partial V}{\partial T}) _ P \ ,\ \ \ (\frac{\partial V}{\partial T}) _ P = V \alpha \\ \beta = - \ \frac { 1 } { V } (\frac{\partial V}{\partial P}) _ T \ , \ \ \ (\frac{\partial V}{\partial P}) _ T = - \ V \beta$$
با قرار دادن روابط فوق در رابطه $$dV = (\frac{\partial V}{\partial P} ) _ P \ d T + (\frac{\partial V}{\partial P} ) _ T \ d P $$، مشتق جزیی حجم به صورت زیر نوشته میشود:
$$d V = V \alpha d T - V \beta d P$$
معادله بهدست آمده میتواند به عنوان شکل دیفرانسیلی معادله حالت در نظر گرفته شود. اگر اطلاعات تجربی ماده در سیستم دسترس باشد، با انتگرالگیری از رابطه $$d V$$ میتوانیم تغییرات حجم برحسب فشار و دما را به طور کامل توصیف کنیم. حالت مشابهی را برای آنتروپی در نظر میگیریم:
$$S = S( T , P)$$
از آنجا که حجم، دما و فشار همگی توابع حالت هستند، تغییرات آنتروپی را میتوانیم به صورت زیر بنویسیم:
$$d S = M d T + N d P$$
ضرایب M و N در رابطه فوق به صورت زیر نوشته میشوند:
$$dS = (\frac{\partial S}{\partial T} ) _ P \ d T + (\frac{\partial S}{\partial P} ) _ T \ d P $$
$$ (\frac{\partial S}{\partial P} ) _ T$$ را در روابط ماکسول بهدست آوردیم:
$$N = (\frac{\partial S}{\partial T}) _ T = - \ ( \frac{\partial V}{\partial T})_ P = - \ V \alpha$$
برای محاسبه ضریب $$(\frac{\partial S}{\partial T} ) _ P $$ باید از بحث ترمودینامیکی مبتنی بر تعریف ظرفیت گرمایی استفاده کنیم. در هر فرایند برگشتپذیر و بر طبق قانون دوم ترمودینامیک، گرمای جذب شده توسط سیستم با تغییر آنتروپی به صورت زیر به یکدیگر مربوط میشوند:
$$\delta Q _ {rev} = T \ d S$$
این رابطه را در رابطه $$dS = (\frac{\partial S}{\partial T} ) _ P \ d T + (\frac{\partial S}{\partial P} ) _ T \ d P $$ و به جای dS قرار میدهیم:
$$\delta Q _ { rev} = T [ (\frac{\partial S}{\partial T} ) _ P \ d T + (\frac{\partial S}{\partial P} ) _ T \ d P] $$
گرمای جذب شده در فرایندِ فشار ثابت ($$d P = 0$$) به صورت زیر نوشته میشود:
$$\delta Q _ { rev} = T (\frac{\partial S}{\partial T} ) _ P \ d T $$
اندازهگیری گرمای جذب شده در فرایندِ فشار ثابت راهی تجربی برای بهدست آوردن مقدار $$C_P$$ است. ظرفیت گرمایی در فشار ثابت به صورت زیر نوشته میشود:
$$\delta Q _ {rev , P } = \equiv C_ P \ d T _ P $$
با مقایسه دو رابطه $$\delta Q _ { rev} = T (\frac{\partial S}{\partial T} ) _ P \ d T $$ و $$\delta Q _ {rev , P } = \equiv C_ P \ d T _ P $$، ظرفیت گرمایی در فشار ثابت با استفاده از رابطه زیر بهدست میآید:
$$C_ P = T \ (\frac{\partial S}{\partial T}) _ P$$
رابطه فوق را به صورت زیر نیز میتوانیم بنویسیم:
$$\frac { C_ P } { T } = \ (\frac{\partial S}{\partial T}) _ P$$
بنابراین، رابطه دیفرانسیلی کلی برای تغییرات آنتروپی نسبت به دما و فشار برای هر سیستم ساده برابر است با:
$$S = S ( T , P ) \enspace \enspace \enspace dS = \frac { C _ P } { T } \ dT - V \alpha d P$$
اگر $$C_P$$ و $$\alpha $$ به عنوان توابعی از دما و فشار برای سیستم مورد بررسی شناخته شده باشند، آنتروپی سیستم ممکن است با انتگرالگیری از رابطه فوق محاسبه شود.
مثال محاسبه آنتروپی سیستم برحسب دما و حجم
برای بهدست آوردن رابطه بین آنتروپی، دما و حجم، مراحل زیر را به ترتیب طی میکنیم.
مرحله اول
آنتروپی را به عنوان تابعی از دما و حجم در نظر میگیریم و آن را به صورت زیر مینویسیم:
$$S = S ( T , V )$$
مرحله دوم
مشتق آنتروپی را نسبت به دما و حجم مینویسیم:
$$d S = M d T + N d V$$
مرحله سوم
به جدول توابع حالت ترمودینامیک برحسب متغیرهای مستقل دما و فشار مراجعه میکنیم.
| $$d V = V \alpha d T - V \beta d P$$ | $$V = V ( T , P )$$ |
| $$dS = \frac { C_ P } { T } d T - V \alpha d P$$ | $$S = S ( T , P )$$ |
| $$d U = ( C _ P - P V \alpha ) d T + V ( p \beta + T \alpha) d P$$ | $$U = U ( T , P )$$ |
| $$d H = C _ P d T + V ( 1- T \alpha) d P$$ | $$H = H ( T , P )$$ |
| $$dF = - ( S + PV \alpha) d T + P V \beta d P$$ | $$F = F ( T , P )$$ |
| $$d G = - \ S d T + V d P$$ | $$G = G ( T , P )$$ |
با استفاده از جدول فوق، $$dV$$ را در رابطه $$dS$$ جایگزین میکنیم:
$$dS = M d T + N ( V \alpha d T - V \beta d P )$$
مرحله چهارم
رابطه بهدست آمده در مرحله قبل را به صورت زیر مرتب میکنیم:
$$d S = ( M + N V \alpha) d T - NV \beta d P$$
مرحله پنجم
$$dS$$ در جدول نوشته شده در مرحله سوم به صورت زیر است:
$$dS = \frac { C_ P } { T } d T - V \alpha d P$$
مرحله ششم
رابطههای نوشته شده برای $$dS$$ در دو مرحله ۴ و ۵ را برابر یکدیگر قرار میدهیم:
$$( M + N V \alpha) d T - NV \beta d P = \frac { C_ P } { T } d T - V \alpha d P$$
ضریبهای $$dT$$ و $$dP$$ را برابر یکدیگر قرار میدهیم:
$$( M + N V \alpha) = \frac { C _ P } { T } \\ - NV \beta= - V \alpha$$
مرحله هفتم
در مرحله ششم به دو معادله و دو مجهول برای ضریبهای M و N رسیدیم. این ضریبها را از حل این دو معادله به صورت زیر بهدست میآوریم:
$$N = \frac { \alpha } { \beta } \\ M = \frac { C _ P } { T } - \frac { \alpha ^ 2 V } { \beta } = \frac { 1 } { T } ( C _ P - \frac { TV \alpha ^ 2 } { \beta } )$$
مرحله هشتم
M و N را در رابطه نوشته شده برای $dS$$ جایگزین میکنیم:
$$dS = \frac { 1 } { T } ( C _P - \frac { T V \alpha ^ 2 } { \beta } ) d T + \frac { \alpha } { \beta } d V$$
مثال محاسبه آنتروپی سیستم برحسب دما و فشار
برای بهدست آوردن رابطه بین آنتروپی، دما و فشار، مراحل زیر را به ترتیب طی میکنیم.
مرحله اول
آنتروپی را به عنوان تابعی از دما و فشار در نظر میگیریم و آن را به صورت زیر مینویسیم:
$$S = S ( P , V )$$
مرحله دوم
مشتق آنتروپی را نسبت به دما و فشار مینویسیم:
$$d S = M d P + N d V$$
مرحله سوم
به جدول توابع حالت ترمودینامیک برحسب متغیرهای مستقل دما و فشار در قسمت قبل مراجعه میکنیم. با استفاده از جدول فوق، $$dV$$ را در رابطه $$dS$$ جایگزین میکنیم:
$$d S = M d P + N ( V \alpha d T - V \beta d P )$$
مرحله چهارم
رابطه بهدست آمده در مرحله قبل را به صورت زیر مرتب میکنیم:
$$d S = N V \alpha d T - N V \beta d P$$
مرحله پنجم
$$dS$$ در جدول نوشته شده در مرحله سوم به صورت زیر است:
$$dS = \frac { C_ P } { T } d T - V \alpha d P$$
مرحله ششم
رابطههای نوشته شده برای $$dS$$ در دو مرحله ۴ و ۵ را برابر یکدیگر قرار میدهیم:
$$NV \alpha d T + ( M + N V \beta) d P = \frac { C _ P } { T } - V \alpha d P$$
ضریبهای $$dT$$ و $$dP$$ را برابر یکدیگر قرار میدهیم:
$$ٰ\ N V \alpha = \frac { C_ P } { T } \\ M - N V \beta = - V \alpha$$
مرحله هفتم
در مرحله ششم به دو معادله و دو مجهول برای ضریبهای M و N رسیدیم. این ضریبها را از حل این دو معادله به صورت زیر بهدست میآوریم:
$$ٔN = \frac { C _ P } { T V \alpha} \\ M = \frac { C_ P \beta } { T \alpha} - V \alpha$$
مرحله هشتم
M و N را در رابطه نوشته شده برای $dS$$ جایگزین میکنیم:
$$d S = \frac { 1 } { T } ( C _ P - \frac { TV \alpha ^ 2 } { \beta} ) d T + \frac { \alpha} { \beta} d V$$
تاکنون با برخی از مهمترین فرمول های ترمودینامیک و اثبات آنها در فیزیک آشنا شدیم. در ادامه، مهمترین فرمول های ترمودینامیک در مهندسی مواد را بیان و اثبات میکنیم.
فرمول های ترمودینامیک در علم مواد
ترمودینامیک نقش مهمی در مهندسی مواد و داشتن درک بهتری از رفتار و ویژگیهای مواد ایفا میکند. در ادامه، برخی از مهمترین فرمول های ترمودینامیک در علم مواد را با یکدیگر مطالعه میکنیم.
رابطه کلازیوس-کلاپیرون
فرمول کلازیوس کلاپیرون یکی از مهمترین فرمول های ترمودینامیک در علم مواد است. در این بخش، با استفاده از قانون اول ترمودینامیک و تعریف انرژی آزاد گیبس، رابطه کلازیوس-کلاپیرون را اثبات میکنیم. معادله کلازیوس کلاپیرون راهی برای توصیف تبدیل فاز ناپیوسته بین دو فاز ماده از جزیی واحد است. بین دمای مایع و فشار بخار آن، خط مستقیمی وجود ندارد. به عنوان مثال، فشار بخار در آب، بسیار سریعتر از دمای سیستم افزایش مییابد. معادله کلازیوس این عمل را توصیف میکند. دمای سیستم تعادل بین مایع و بخار آن را تعیین میکند. افزایش دما، فشار بخار مایع را افزایش میدهد. معادله کلازیوس کلاپیرون به صورت زیر نوشته میشود:
$$\ln \frac { P _ 2 } { P _ 1 } = \frac { \triangle H _ { vap } } { R } ( \frac { 1 } { T _ 1 } - \frac { 1 } { T _ 2 } )$$
اثبات معادله کلازیوس کلاپیرون
معادله کلازیوس کلاپیرون نرخ افزایش فشار بخار بر واحد افزایش دما برای مادهای با فشار بخار P و دمای T را پیشبینی میکند.
$$\frac{\text{d}lnp}{\text{d}T} = \frac { \triangle H _ { cap } } { R T _ 2 }$$
آنتالپی مولی تبخیر مایع، ثابت گاز ایدهال و دمای سیستم، آهنگ تغییر لگاریتم طبیعی فشار بخار مایع نسبت به دما را با توجه به معدله فوق تعیین میکند. اگر آنتالپی بخار، $$H_ {vap }$$، مستقل از دمای سیستم باشد، معادله کلاسیوس کلاپیرون را میتوان به شکل انتگرالی نوشت.
$$\int \frac{\text{d}lnp}{\text{d}T} = \int \frac { \triangle H _ { cap } } { R T _ 2 } \\ \ln ( P ) + C = - \ \frac { \triangle H _ { vap } } { R T } + \ln A$$
در معادله فوق:
- دما، T، باید برحسب کلوین باشد.
- R ثابت جهانی گازها است.
- A ثابتی است که مقدار آن توسط ماهیت شیمیایی ماده تعیین میشود.
- C ثابت انتگرالگیری است.
از آنجا که رابطه بین دما و فشار بخار خطی نیست، معادله به منظور برقراری رابطه خطی به شکل لگاریتمی نوشته میشود. اگر آنتالپی تبخیر و فشار بخار در هر دما برای هر مایعی تعریف شده باشند، از معادله کلازیوس کلاپیرون میتوانیم برای محاسبه فشار بخار در دماهای مختلف استفاده کنیم. در این صورت، معادله خطی میتواند به شکل دو نقطهای نوشته شود. اگر فشار بخار در دمای $$T_1$$ برابر $$P_1$$ و در دمای $$T_2$$ برابر $$P_2$$ باشد، معادلات خطی در هر دما و فشار بخار را میتوانیم به شکل زیر بنویسیم:
$$\ln ( P _ 1) + C = - \ \frac { \triangle H _ { vap } } { R T _ 1 } + \ln A \\ \ln ( P _ 2 ) + C = - \ \frac { \triangle H _ { vap } } { R T _ 2 } + \ln A$$
ثابتهای A و C در هر دو معادله با یکدیگر برابر هستند. معادله $$\ln ( P _ 2 ) + C = - \ \frac { \triangle H _ { vap } } { R T _ 2 } + \ln A$$ را از معادله $$\ln ( P _ 1 ) + C = - \ \frac { \triangle H _ { vap } } { R T _ 1 } + \ln A$$ کم میکنیم.
$$\ln ( P _ 2 ) - \ln ( P _ 1 ) = [ - \ \frac { \triangle H _ { vap }} { R T _2} + \ln A ] - [ - \ \frac { \triangle H _ { vap }} { R T _1} + \ln A ] \\ \ln ( \frac { P _2 } { P _ 1 } ) = \frac { \triangle H _ { vap }} { R } \ ( \frac { 1 } { T _ 1 } - \frac { 1 } { T _2 } )$$
این معادله به شکلهای دیگری نیز نوشته میشود. اگر بخواهیم فشار بخار را در دمای جدید بهدست آوریم، از معادله زیر استفاده میکنیم:
$$P_ 2 = P _1 e ^ { - \ \frac { \triangle H _ { vap } } { R } ( \frac { 1 } { T _ 2 } - \frac { 1 } { T _ 1 } )}$$
گاهی باید گرما را بهدست آوریم. برای این کار از معادله زیر استفاده میکنیم:
$$\triangle H _ { vap } = \frac { - \ R \ln (\frac { P _ 2 } { P _ 1 })} { \frac { 1 } { T _ 2 } - \frac { 1 } { T _ 1 } }$$
گاهی ممکن است بخواهیم دمای ثانویه را بهدست آوریم. برای این کار میتوانیم از معادله زیر استفاده کنیم:
$$T_ 2 = [ \frac { 1 } { T _ 1 } - \frac { R \ln ( \frac { P _ 2 } { P _1 } )} { \triangle H _ { vap}}]^ { -1}$$
با توجه به مقداری که باید بهدست آوریم، یکی از معادلههای بالا را انتخاب میکنیم.
مثال اول معادله کلازیوس کلاپیرون
فشار بخار مادهای در دمای ۳۰۰ کلوین برابر $$21 \ torr$$ است. فشار بخار را در دمای ۳۱۰ کلوین بهدست آورید. آنتالپی تبخیر باربر ۲۴ کیلوژول بر مول است.
پاسخ
با توجه به صورت مثال، فشار ثانویه پس از افزایش دما به اندازه ۱۰ کلوین را باید بهدست آوریم. از اینرو، از میان رابطههای نوشته شده در بالا، رابطه زیر را انتخاب میکنیم:
$$P_ 2 = P _1 e ^ { - \ \frac { \triangle H _ { vap } } { R } ( \frac { 1 } { T _ 2 } - \frac { 1 } { T _ 1 } )}$$
مقدارهای داده شده در رابطه بالا را جایگزین و مقدار فشار ثانویه را بهدست میآوریم:
$$P_ 2 = 21 e ^ { - \ \frac { 24000 } { 8.3145 } ( \frac { 1 } { 310 } - \frac { 1 } { 300 } )} \\ P_ 2 = 26.8 \ torr $$
به این نکته توجه داشته باشید که آنتالپی تبخیر برابر ۲۴ کیلوژول بر مول است و برای بهدست آوردن فشار ثانویه باید آن را به ژول بر مول تبدیل کنیم. با افزایش دما، فشار جزیی نیز افزایش خواهد یافت.
مثال دوم معادله کلازیوس کلاپیرون
فشار بخار مادهای در دمای ۲۵۰ کلوین برابر $$30 \ torr$$ است. در چه دمایی فشار بخار ماده برابر $$150 \ torr $$ خواتهد بود؟ آنتالپی تبخیر برابر ۴۵ کیلوژول بر مول است.
پاسخ
با توجه به صورت مثال، دمای ثانویه پس از افزایش فشار بخار به اندازه $$120 \ torr$$ را باید بهدست آوریم. از اینرو، از میان رابطههای نوشته شده در بالا، رابطه زیر را انتخاب میکنیم:
$$T_ 2 = [ \frac { 1 } { T _ 1 } - \frac { R \ln ( \frac { P _ 2 } { P _1 } )} { \triangle H _ { vap}}]^ { -1}$$
مقدارهای داده شده در رابطه بالا را جایگزین و مقدار دمای ثانویه را بهدست میآوریم:
$$T_ 2 = [ \frac { 1 } { 250 } - \frac { 8.3145 \ln ( \frac { 150 } { 30 } )} { 45000}]^ { -1} = 270.1 \ K $$
تعادل فازی
از دوران دبیرستان و در کتاب علوم آموختیم ماده سه حالت اصلی جامد، مایع و گاز دارد. در این بخش، تعادل فازی بین فازها یا حالتهای مختلف ماده را به صورت خلاصه بررسی میکنیم. پایداری فازهای مختلف را میتوانیم با استفاده از پتانسیل شیمیایی پیشبینی کنیم، به گونهای که پایدارترین حالت ماده، کمینه پتانسیل شیمیایی را در دما و فشارِ داده شده دارد. این مورد را میتوان در نمودار فازی به صورت نشان داده شده در تصویر زیر خلاصه کرد.
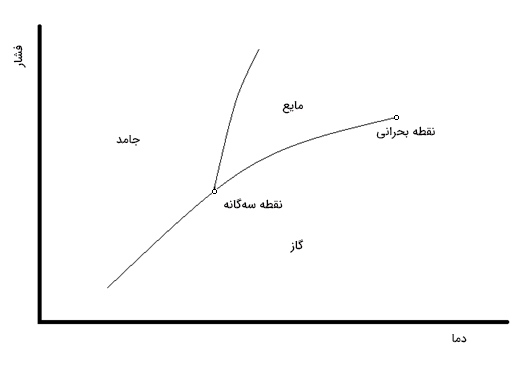
در نمودار فازی نشان داده شده در تصویر بالا، مرزهای فازی میتوانند توسط اندازهگیری نرخ سرد شدن در دمای ثابت تعیین شوند. نمودار خنککنندهای در تصویر زیر نشان داده شده است. دما با گذشت زمان کاهش خواهد یافت. تغییر فاز رخ میدهد و حالت ماده از مایع به جامد تغییر میکند. به هنگام تغییر فاز ماده، دما ثابت خواهد ماند. دمای ثابتی که در آن تغییر فاز رخ میدهد، نقطهای را روی مرز دمای ثابت و فشاری که در آن نمودار خنککننده اندازه گرفته میشود، ایجاد خواهد کرد.

مشخصه ترمودینامیکی برای تعادل فازی بسیار ساده و بر پایه پتانسیلهای شیمیایی اجزای تشکیلدهنده سیستم است. برای سادگی سیستمی با یک جزء را در نظر بگیرید. برای آنکه تمام سیستم در حالت تعادل قرار داشته باشد، پتانسیل شیمیایی هر جزء در هر فاز باید یکسان باشد. در غیر این صورت، مقداری جرم از فازی به فاز دیگر میرود. در این حالت، پتانسیل شیمیایی کل فازی که ماده از آن خارج میشود کاهش و پتانسیل شیمیایی فازی که ماده به آن وارد میشود، افزایش خواهد یافت. بنابراین، برای هر جفت فاز حاضر ($$\alpha $$ و $$\beta$$) رابطه زیر باید برقرار باشد:
$$\mu_ { alpha} = \mu _ { beta} $$
قانون فازی گیبس
قانون فازی گیبس تعداد متغیرهای ترکیبی و فازی که میتوانند آزادانه برای هر سیستم تعادلی تغییر کنند را توصیف میکنند. برای هر فاز موجود در سیستم، کسر مولی تمام اجزای سیستم به جز یکی از آنها میتوانند به صورت مستقل تغییر کنند:
$$\sum_i \chi_ i = 1$$
معادله کلاپیرون
بر طبق مشخصه ترمودینامیکی گفته شده برای تعادل، میتوانیم به نتایجی در مورد متغیرهای حالت مانند فشار و دما و رابطه آنها با یکدیگر در امتداد مرزهای فازی برسیم. در نخستین گام پتانسیلهای شیمیایی دو فاز $$\alpha $$ و $$\beta$$ باید با یکدیگر برابر باشند:
$$\mu_ { alpha} = \mu _ { beta} $$
همچنین، هر تغییر بینهایت کوچکی در پتانسیل شیمیایی یکی از فازها باید تغییر بسیار کوچکی در فاز شیمیایی فاز دیگر جبران شود.
$$\mu_ { \alpha } + d \mu_ { \alpha } = \mu_ { \beta } + d \mu_ { \beta }$$
از آنجا که $$\mu_ { alpha} = \mu _ { beta} $$، آنها را از طرفین رابطه بالا حذف میکنیم. بنابراین، داریم:
$$d \mu_ { \alpha } = d \mu_ { \beta }$$
پتانسیل شیمیایی را میتوان برحسب حجم و آنتروپی مولی نوشت:
$$d \mu = V d p - S d T$$
برای نگه داشتن تعادل بین فازهای مختلف، تغییرات دما و فشار با محدودیت همراه است:
$$V_ { \alpha } d P - S_ { \alpha } d T = V _ { \beta } d P - S _ { \beta } d T$$
تساوی زیر را برحسب تغییرات فشار و دما مرتب میکنیم:
$$( V _ { \alpha } - V _ { \beta }) d P = ( S _ { \alpha } - S _ { \beta } ) d T$$
( V _ { \alpha } - V _ { \beta }) و ( S _ { \alpha } - S _ { \beta } ) به ترتیب برابر تغییرات حجم و آنتروپی مولی برای تغییرات فازی هستند. بنابراین، عبارت فوق را میتوانیم به صورت زیر بنویسیم:
$$\triangle V d p = \triangle S d T \\ \frac{\text{d}p}{\text{d}T} = \frac { \triangle S } { \triangle V }$$
به این معادله، معادله کلاپیرون میگوییم. با استفاده از این رابطه میتوانیم ببینیم چگونه نمودار فازی آب به صورت کیفی با مواد دیگر تفاوت دارد. به این نکته توجه داشته باشید که معادله کلازیوس کلاپیرون که در بخش قبل در مورد آن صحبت کردیم نیز معادله مهمی در تعادل فازی و نمودارهای فازی است.
جمعبندی
در این مطلب در مورد فرمول های ترمودینامیک صحبت کردیم. ترمودینامیک علمی است که در آن در مورد رابطه بین گرما، کار، دما و انرژی صحبت میکنیم و انتقال انرژی از نقطهای به نقطه دیگر و از شکلی به شکل دیگر را توضیح میدهیم. ابتدا فرمول های ترمودینامیک حاکم بر گاز کامل را با حل چند مثال توضیح دادیم. مهمترین فرمول های ترمودینامیک برای گاز کامل در جدول زیر به صورت خلاصه آمده است:
| رابطه گاز کامل | $$PV = n R T$$ |
| تبدیل دما از سلسیوس به کلوین | $$ T _ K = T _ C + 273$$ |
| قانون بویل | $$P _ 1 V_ 1 = P_2 V_2$$ |
| قانون شارل | $$\frac { V_ 1 } { T _ 1} = \frac { V_2 } { T_ 2 }$$ |
| قانون گیلوساک | $$\frac { P_ 1 } { T _ 1} = \frac { P_2 } { T_ 2 }$$ |
| قانون آووگادرو | $$\frac { V_ 1 } {n _ 1} = \frac { V_2 } { n _ 2 }$$ |
| قانون دالتون برای فشار جزیی | $$P _ T = P _ 1 + P _2 + P _ 3 + ...$$ |
| میانگین سرعت کل مولکولهای گاز | $$v = \sqrt{\frac{ 3 R T }{M}}$$ |
سپس، فرمول های ترمودینامیک برای گاز واقعی را بهدست آوردیم. گرچه مدل گاز ایدهال اطلاعات نسبتا درستی در مورد رفتار گازها به ما میدهد، باید بدانیم هیچ گازی به طور کامل ایدهال نیست. ابتدا فشار گاز را با اضافه کردن عبارت $$\frac { a n ^ 2 } { V ^ 2 }$$ اصلاح میکنیم. این عبارت به جاذبه بین ذرات تشکیلدهنده گاز مربوط میشود. a در این عبارت ثابتی است که قدرت نیروی جاذبه بین ذرات گاز را توصیف میکند. مقدار این نیرو با نوع ذرات تشکیلدهنده گاز ارتباط دارد. هرچه مولکولها بزرگتر و قطبیدهتر باشند، نیروی جاذبه بین آنها قویتر خواهد بود. در ادامه، عبارت $$nb$$ را از حجم کم میکنیم. $$nb$$ حجم اشغال شده توسط ذرات گاز است. مهمترین فرمول های ترمودینامیک برای گاز واقعی در جدول زیر نوشته شدهاند.
| معادله گاز کامل | $$( P + \frac { a n ^ 2 } { V ^ 2 } ) ( V - nb ) = n R T$$ |
| معادله ردلیش کوانگ | $$P = \frac {RT} {V - b} - \frac {a } {(V(V + b) \times √T)} $$ |
| معادله پنگ رابینسون | $$P = \frac {RT} {V - b} - \frac {a [ 1 + k( 1 - \sqrt {\frac {T } {T _C}})^ 2] } {(V(V + b) +b( V - b)} $$ |
در ادامه مطلب و پس از اثبات مهمترین فرمول های ترمودینامیک برای گاز کامل و گاز واقعی، فرمولهای مهم قانون اول و دوم ترمودینامیک را با یکدیگر بهدست آوردیم.
| رابطه مهم قانون اول ترمودینامیک | $$\triangle U = Q + W$$ |
| رابطه بین ضریب انبساط گرمایی، $$\alpha$$، و تراکمپذیری همدما، $$k_T$$ | $$( \frac{\partial P}{\partial T})_V = \frac { \alpha } { \ k_T }$$ |
| آفزایش آنتروپی در فرایندهای خودبهخودی و قانون دوم ترمودینامیک | $$\triangle S > 0$$ |
| بازده موتور کارنو | $$\eta = 1 - \frac { T_2 } { T _ 1 }$$ |
| رابطه اول ماکسول، شروع از رابطه $$d U = T d S - P dV $$ | $$(\frac{\partial P}{\partial S})_ S = - \ (\frac{\partial P}{\partial S}) _ V$$ |
| رابطه دوم ماکسول، شروع از رابطه $$H = U + PV$$ | $$(\frac{\partial T}{\partial P})_ S = \ (\frac{\partial V}{\partial S}) _ P$$ |
| رابطه سوم ماکسول، شروع از رابطه $$A = U - TS$$ | $$- \ (\frac{\partial P}{\partial T})_ V = \ (\frac{\partial S}{\partial V}) _ T$$ |
| رابطه چهارم ماکسول، شروع از رابطه $$ G = H - TS $$ | $$- \ (\frac{\partial V}{\partial T})_ P = - \ (\frac{\partial S}{\partial P}) _ T$$ |
| ظرفیت گرمایی در حجم ثابت | $$C_V = - \ (\frac{\partial U }{\partial V} ) _ T (\frac{\partial V}{\partial T})_ U$$ |
| تغییرات انرژی آزاد گیبس نسبت به فشار | $$G ( P_ 2 ) = G ( P _ 1 ) + n R T \ln \frac { P _ 1 } { P _ 1 }$$ |
| تغییرات آنتروپی و حجم نسبت به دما و فشار | $$S = S ( T , P ) \enspace \enspace \enspace dS = \frac { C _ P } { T } \ dT - V \alpha d P$$ |
در پایان، در مورد فرمول های ترمودینامیک در علم مواد و تعادل فازی صحبت کردیم. نخستین معادله مهم در علم مواد رابطه کلازیوس-کلاپیرون است و به صورت زیر نوشته میشود:
$$\ln \frac { P _ 2 } { P _ 1 } = \frac { \triangle H _ { vap } } { R } ( \frac { 1 } { T _ 1 } - \frac { 1 } { T _ 2 } )$$
این معادله سه شکل دیگر نیز دارد:
- اگر بخواهیم فشار بخار را در دمای جدید بهدست آوریم، از معادله زیر استفاده میکنیم:
$$P_ 2 = P _1 e ^ { - \ \frac { \triangle H _ { vap } } { R } ( \frac { 1 } { T _ 2 } - \frac { 1 } { T _ 1 } )}$$
- برای به دست آوردن گرما یا آنتالپی از معادله زیر استفاده میکنیم:
$$\triangle H _ { vap } = \frac { - \ R \ln (\frac { P _ 2 } { P _ 1 })} { \frac { 1 } { T _ 2 } - \frac { 1 } { T _ 1 } }$$
- برای بهدست آوردن دمای ثانویه از معادله زیر استفاده کنیم:
$$T_ 2 = [ \frac { 1 } { T _ 1 } - \frac { R \ln ( \frac { P _ 2 } { P _1 } )} { \triangle H _ { vap}}]^ { -1}$$










