توابع حالت و اهمیت آنها در انرژی درونی — از صفر تا صد
در مطالب قبلی مجله فرادرس، تابع حالت و تفاوت آن با تابع مسیر را شناختیم و بررسی کردیم. در این آموزش قصد داریم به اهمیت این توابع حالت در علم شیمیفیزیک و ترمودینامیک بپردازیم. در حقیقت، از خواص ریاضی توابع حالت بمنظور تعریف مقادیر دیفرانسیلی $$dH$$ و $$dU$$ به عنوان دیفرانسیل کامل استفاده میشود. با این کار، روابطی را بدست میآوریم که تغییرات $$U$$ با دما و حجم و تغییرات $$H$$ با دما و فشار را به مقادیر آزمایشگاهی در دسترس همچون ظرفیت حرارتی مرتبط میکند.
با وجود اینکه انرژی درونی و آنتالپی، هردو تابعی از متغیرهای فشار، حجم و دما هستند اما وابستگی انرژی درونی و آنتالپی به دما، بسیار بیشتر از دو متغیر دیگر است. بنابراین، در بیشتر فرآیندهای شامل گاز، مایع و جامد، انرژی درونی و آنتالپی را تنها میتوان تابعی از $$T$$ دانست. از جمله موارد استثنا هم میتوان به فرآیند سردسازی در انبساط «همآنتالپی» (Isenthalpic) گازهای واقعی اشاره کرد که به طور تجاری برای مایع کردن گازهای نیتروژن، اکسیژن، هلیوم و آرگون مورد استفاده قرار میگیرد.
خواص ریاضی توابع حالت
در مباحث قبلی مجله فرادرس، نشان دادیم که $$U$$ و $$H$$، توابع حالت و $$w$$ و $$q$$، توابع مسیر هستند. همچنین نحوه محاسبه تغییرات این مقادیر را برای گاز ایدهآل بیان کردیم. در ادامه سعی داریم تا از خاصیت توابع حالت استفاده کنیم تا رابطهای بدست بیاوریم که تغییرات انرژی درونی و آنتالپی را به عنوان تابعی از فشار، حجم و دما محاسبه کنیم. این رابطه در گازهای گازهای حقیقی، مایعات و جامدات مورد استفاده قرار میگیرد. نشان میدهیم که ساختار قراردادی ترمودینامیک، ابزار قدرتمندی را در اختیار ما قرار میدهد که بوسیله آن مباحث تئوری و عملی را به یکدیگر مرتبط کنیم. البته قبل از اینکه به توضیح این موارد بپردازیم، خواص ریاضی توابع حالت را باید بیان کنیم.
توابع حالت ترمودینامیکی مورد نظر را به کمک دو متغیر از متغیرهای P،V و T تعریف میکنیم. در فرمولبندی تغییرات تابع حالت، از مشتق جزئی بهره میگیریم. لازم به ذکر است که مباحث مطرح شده را نمیتوان برای توابع مسیر $$w$$ و $$q$$ بکار گرفت زیرا روابطی همچون رابطه زیر، در توابع مسیر وجود ندارند. ۱ مول گاز ایدهآل را در نظر بگیرید که در آن، رابطه زیر برقرار است:
$$\begin {equation} P = f ( V, T ) =\frac {R T} {V} \end {equation}$$
توجه داشته باشید که فشار را میتوان به صورت تابعی از دو متغیر دما و حجم نوشت. تغییرات فشار در نتیجه تغییرات حجم یا دما، با مشتق جزئی روابط زیر متناسب است:
$$\begin{equation} \begin {aligned}
\left (\frac {\partial P } {\partial V} \right) _ { T } &= \lim _ {\Delta V \rightarrow 0} \frac { P ( V + \Delta V, T ) - P ( V , T) } { \Delta V } = - \frac { R T } { V ^ { 2 } } \\
\left ( \frac { \partial P} {\partial T } \right ) _ { V } & = \lim _ { \Delta T \rightarrow 0} \frac{ P ( V , T + \Delta T) - P ( V, T ) }{ \Delta T } = \frac { R } { V }
\end {aligned} \end {equation}$$
زیروند T در رابطه $$ (\frac {\partial P } {\partial V} ) _ { T }$$ نشاندهنده این است که $$T$$ نسبت به $$V$$ ثابت است. مشتقهای جزئی در روابط بالا سبب میشوند که تغییرات یک تابع را به هنگام تغییر متغیرها بررسی کنیم. به طور مثال، مقدار تغییرات $$P$$ چه میزان خواهد بود اگر مقادیر $$T$$ و $$V$$ هر دو تغییر کنند؟ در این شرایط، به $$P+dP$$ تبدیل میشود که برای $$dP$$ داریم:
$$\begin{equation} d P =\left (\frac {\partial P} {\partial T } \right) _ {V} d T + \left (\frac {\partial P } {\partial V } \right ) _ { T } d V \end {equation}$$
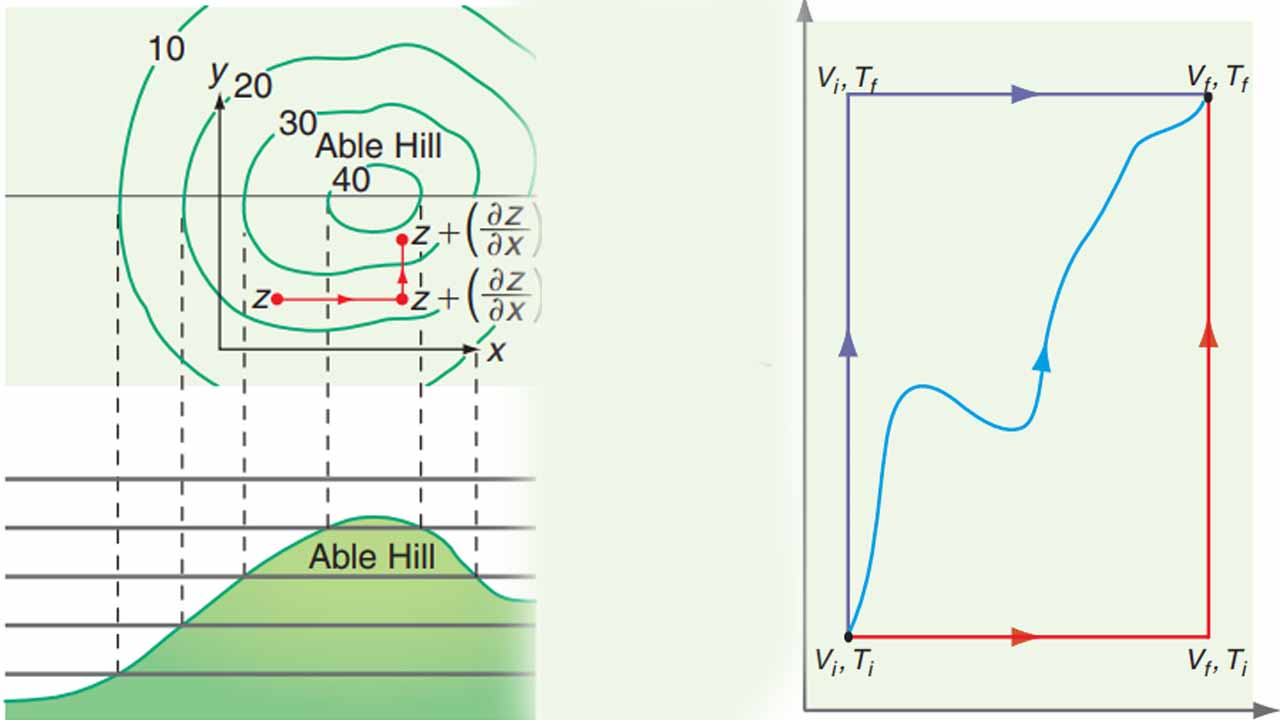
برای درک بهتر رابطه بالا، تصویر زیر را در نظر بگیرید. شخصی بر روی تپهای قرار دارد که ارتفاع آن شخص از سطح دریا مشخص است. اگر شخص، فاصله بسیاری کمی (x) را به سمت شرق و شمال (y) طی کند، تغییرات ارتفاع (z) چقدر خواهد بود؟ تغییرات z به هنگام حرکت شخص به شرق، برابر با شیب تپه $$\begin{equation} \left (\frac {\partial Z} {\partial x } \right) _ {y} \end {equation}$$ ضربدر فاصله $$dx$$ طی شده توسط شخص خواهد بود. رابطهای مشابه نیز برای حرکت به سمت شمال میتوان نوشت. بنابراین، تغییرات کلی ارتفاع، برابر با مجموع تغییر حرکت در جهتهای شرق و شمال خواهد بود. این تغییرات ارتفاع در جهات x و y در تصویر زیر نشان داده شده است.
$$\begin {equation} d z = \left (\frac { \partial z } {\partial x } \right ) _ {y} d x+ \left (\frac {\partial z} {\partial y} \right) _{x} d y \end {equation}$$
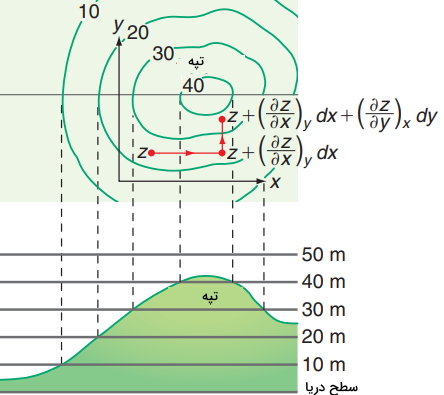
از آنجایی که شیب تپه، تابعی غیرخطی از x و y است، رابطه بالا برای $$dz$$ تنها برای تغییرات بسیار کوچک و دیفرانسیلی $$dx$$ و $$dy$$ صدق میکند. در غیر اینصورت، باید از مشتق مراتب بالاتر استفاده کنیم. برای توصیف این حرکت، از مشتق مرتبه دوم یا بیشتر نیز میتوان کمک گرفت. در این رابطه از مشتق جزئی مخلوط P بهره میگیریم که رابطه آن به شکل زیر است:
$$\begin {equation} \begin {aligned}
& \left (\frac {\partial} {\partial T } \left (\frac {\partial P}{\partial V } \right ) _ { T } \right ) _ { V } = \frac{\partial ^ {2} P} {\partial T \partial V}= \left( \partial \left ( \frac { \partial \left [\frac { R T} { V} \right] } {\partial V} \right) _ { T } / \partial T \right) _ {V} = \left (\partial \left [-\frac { R T }{ V ^{2}} \right] / \partial T \right) _ { V } = - \frac{R} {V^{2}}\\
&\left ( \frac { \partial} {\partial V } \left ( \frac {\partial P}{\partial T} \right) _ { V} \right) _ { T } = \frac {\partial ^ { 2 } P } {\partial V \partial T} = \left(\partial \left (\frac {\partial \left [\frac {R T} {V} \right] } { \partial T } \right) _ {V} / \partial V \right) _ {T} = \left (\partial \left [ \frac {R} {V} \right] / \partial V \right) _ { T } =- \frac {R} {V ^{2}}
\end {aligned} \end{equation}$$
برای تمامی توابع f و در این مورد خاص، P، مرتبهای که از تابع مشتق میگیریم، تاثیری بر نتیجه نهایی نخواهد داشت. به همین دلیل رابطه زیر را میتوان نتیجه گرفت:
$$\begin {equation} \left ( \frac { \partial} {\partial T } \left ( \frac { \partial f( V , T ) } {\partial V } \right ) _ { T } \right ) _{V}= \left( \frac {\partial} {\partial V } \left( \frac {\partial f(V, T)}{ \partial T} \right) _{V} \right) _ {T} \end {equation}$$
با توجه به اینکه رابطه بالا تنها در توابع حالت صدق میکند، از این رابطه میتوان برای مشخص کردن تابع حالت بودن تابعی همچون f استفاده کرد. اگر f جزو توابع حالت باشد، رابطه زیر برای آن برقرار است:
$$\begin {equation} \Delta f = \int _ {i} ^ {f} d f = f_ {\text {final} } -f _{\text {initial} } \end {equation}$$
این رابطه بیان میکند که f را میتوان به صورت یک مقدار دیفرانسیلی و کوچک بیان کرد که اگر از آن انتگرال بگیریم، جواب انتگرال تنها به حالات اولیه و نهایی وابسته است که در این حالت، به $$df$$، دیفرانسیل کامل میگویند. نمونهای از یک تابع حالت، انرژی درونی $$U$$ است که دیفرانسیل کامل آن به صورت زیر نوشته میشود. خطی که روی dq قرار گرفته نشاندهنده دیفرانسیل کامل نبودن آن است:
$$\require {cancel} \begin {equation}d U=\cancel d q - P _ {\text {external} } d V \end {equation}$$
در ادامه، مثالهایی برای بررسی قرارگیری یک تابع به عنوان توابع حالت، مطرح و روابط ریاضی آنرا با یکدیگر مرور میکنیم.
مثال برای بررسی توابع حالت
تابع زیر را در نظر بگیرید:
$$\begin {equation} f ( x , y ) = y e ^ { x } + x y + x \ln y \end {equation}$$
- مشتقهای زیر را برای این تابع حساب کنید:
$$\begin {equation} \left ( \frac { \partial f} {\partial x } \right ) _ { y } , \left (\frac {\partial f } {\partial y } \right ) _ { x } \left( \frac { \partial ^ {2} f} {\partial x ^ {2}}\right) _{y}, \left ( \frac {\partial^ {2} f } {\partial y ^{2} } \right) _ {x} , \left ( \frac { \partial \left( \frac {\partial f } {\partial x}\right ) _ {y}}{\partial y } \right ) _ {x}, \operatorname{} \left (\frac {\partial \left (\frac {\partial f} {\partial y} \right ) _ { x}} {\partial x } \right) _ { y} \end {equation}$$
- تابع حالت بودن $$f ( x , y)$$ را برای متغیرهای x و y بررسی کنید.
- اگر $$f ( x , y)$$ تابع حالت باشد، دیفرانسیل کل $$df$$ را محاسبه کنید.
پاسخ
$$\begin {equation} \begin {aligned}
& \left ( \frac { \partial f } { \partial x } \right ) _ { y } = y e ^ { x } +y + \ln y, \quad \left ( \frac {\partial f } {\partial y} \right ) _ { x } = e ^{x} + x+ \frac {x} {y}\\
& \left ( \frac {\partial ^{2} f} { \partial x ^ {2} } \right ) _ {y } = y e ^ {x}, \quad \left ( \frac {\partial ^ { 2 } f } { \partial y ^ {2}} \right) _ { x } = -\frac {x} {y ^{2} }\\
& \left ( \frac { \partial \left ( \frac {\partial f } {\partial x} \right ) _ {y}} {\partial y} \right ) _ {x} = e ^{x} + 1 + \frac{1} {y}, \quad \left ( \frac { \partial \left (\frac {\partial f} { \partial y } \right) _{x}} {\partial x } \right) _ {y} = e ^{x} + 1+ \frac{1} {y}
\end {aligned} \end {equation}$$
$$f ( x , y)$$ از جمله توابع حالت به شمار میآید زیرا در مثال قبل نشان دادیم که رابطه زیر برقرار است. به عبارت دیگر، هر تابعی که بتوان آنرا به شکل تحلیل زیر نشان داد، جزو توابع حالت محسوب میشود.
$$\begin {equation} \left ( \frac { \partial \left ( \frac { \partial f } { \partial x } \right ) _ { y } } { \partial y } \right ) _ { x } = \left ( \frac { \partial \left (\frac {\partial f } { \partial y } \right ) _ { x }} { \partial x } \right ) _ { y } \end {equation}$$
دیفرانس کل نیز از رابطه زیر بدست میآید:
$$\begin {equation} \begin {array} {c}
d f = \left ( \frac {\partial f } { \partial x } \right ) _ {y } d x + \left ( \frac { \partial f} { \partial y } \right ) _ { x} d y \\
= \left ( y e ^ { x } + y +\ln y\right) d x + \left (e ^ {x } + x + \frac { x} {y } \right ) d y
\end {array} \end {equation}$$

قاعده ضرب سه گانه
تابع $$z= f (x , y)$$ را در نظر بگیرید که میتوان آنرا به شکلهای زیر بازآرایی کرد:
$$x= g (y , z)$$ و $$y= h (x , z)$$
به طور مثال اگر تابع $$P = nRT /V$$ را در نظر بگیریم، میتوان آنرا به شکلهای $$V = nRT /P$$ و $$T = PV /nR$$ نوشت. در چنین شرایطی، رابطه زیر برقرار است:
$$\begin {equation} \left ( \frac { \partial x } {\partial y } \right ) _ {z } = \frac{1} {\left ( \frac { \partial y } {\partial x } \right ) _ { z } } \end {equation}$$
همچنین میتوان از «قاعده ضرب سهگانه» (Triple Product Rule) یا قاعده زنجیرهای سهگانه به شکل زیر استفاده کرد:
$$\begin {equation} \left ( \frac { \partial x } {\partial y } \right ) _ { z } \left ( \frac { \partial y } {\partial z } \right)_ {x} \left ( \frac { \partial z} { \partial x } \right) _{y} = -1 \end {equation}$$
به کمک دو رابطه بالا میتوان معادله زیر را به طور مجدد فرمولبندی کرد:
$$\begin {equation} d P = \left ( \frac {\partial P } {\partial T } \right ) _ {V} d T + \left ( \frac {\partial P} {\partial V} \right) _ { T} d V \end {equation}$$
فرض کنید رابطه بالا را بخواهیم برای یک ماده خاص همچون گاز نیتروژن استفاده کنیم. چه مقادیری باید در آزمایشگاه اندازهگیری شوند تا مقادیر عددی برای $$(\frac {\partial P } {\partial T } ) _ {V}$$ و $$\left ( \frac {\partial P} {\partial V} \right) _ { T} $$ بدست بیایند؟ به کمک قاعده ضرب سهگانه خواهیم داشت:
$$\begin {equation} \begin {aligned}
& \left ( \frac { \partial P } { \partial V } \right ) _ { T } \left ( \frac {\partial V} {\partial T} \right) _ {P} \left ( \frac {\partial T } {\partial P} \right) _ { V } = - 1 \\
& \left ( \frac { \partial P } { \partial T } \right ) _ { V } = -\left ( \frac {\partial P } {\partial V} \right ) _ { T } \left ( \frac {\partial V } {\partial T } \right ) _ { P } = -\frac {\left (\frac {\partial V} {\partial T} \right) _ { P}} {\left (\frac {\partial V}{\partial P} \right) _ {T}} = \frac {\beta} {\kappa} \quad \text { , }\\
& \left ( \frac {\partial P} {\partial V } \right ) _ { T } = - \frac{1} {\kappa V}
\end {aligned} \end {equation}$$
در رابطه بالا، عبارتهای $$\beta$$ و $$\kappa$$ به ترتیب، ضریب انبساط حرارتی حجمی همفشار و تراکمپذیری همدما نامیده میشوند که به سادگی قابل اندازهگیری هستند و روابط آنها به شکل زیر تعریف میشوند:
$$\begin{equation} \beta = \frac{1} {V} \left ( \frac {\partial V} {\partial T } \right ) _ {P} \quad \text { } \quad \kappa = -\frac { 1} {V} \left ( \frac {\partial V} {\partial P } \right) _ {T} \end {equation}$$
هر دو مقدار $$\left ( \frac {\partial V} {\partial T } \right ) _ {P}$$ و $$\left ( \frac {\partial V} {\partial P } \right) _ {T}$$ را میتوان به کمک مشخص کردن تغییرات حجم سیستم در اثر تغییر دادن یکی از دو متغیر فشار یا دما، اندازهگیری کرد. علامت منفی برای $$\kappa$$ به این دلیل انتخاب شده است که مقادیر تراکمپذیری همدما مثبت باشند. اگر تغییرات P و T بسیار کم باشند، رابطه بالا را میتوان به شکلهای فشردهتر زیر نوشت:
$$\begin {equation}V \left (T _ { 2 } \right ) = V \left ( T _ {1} \right ) \left ( 1 + \beta \left [T _ {2} -T _ { 1 } \right ] \right ) \end {equation}$$
$$\begin {equation} V \left ( P _ { 2} \right ) = V \left (P_ {1} \right ) \left (1 -\kappa \left[P_ {2} - P_{1} \right ] \right) \end {equation}$$
تمامی روابطی که تا اینجا مطرح شد نشان دادند که چطور مباحث تئوری و عملی به کمک خواص توابع حالت به یکدیگر مرتبط میشوند. به کمک روابطی که برای محسابه $$\kappa$$ و $$\beta$$ بیان کردیم، حال، فرمولبندی جدید را ارائه میدهیم:
$$\begin {equation} d P = \frac {\beta} {\kappa} d T - \frac { 1}{\kappa V } d V \end {equation}$$
که با انتگرالگیری به رابطه زیر میرسیم:
$$\begin {equation} \Delta P= \int_ {T_{i}} ^{T_ {f}} \frac {\beta}{\kappa} d T -\int _ { V _{i}} ^{ V_ {f}} \frac{1}{\kappa V} d V \approx \frac{\beta}{\kappa}\left (T _ {f} - T _{i}\right)-\frac{1}{\kappa} \ln \frac { V _{f }} { V _{ i}} \end {equation}$$
عبارت دوم در رابطه بالا زمانی صحیح است که $$\Delta V$$ و $$\Delta T$$ به اندازه کافی کوچک باشند که $$\beta$$ و $$\kappa$$ به هنگام انتگرالگیری، مقادیر ثابتی داشته باشند. در مثال زیر، کاربرد عملی این رابطه را بررسی میکنیم.
مثال برای ضریب انبساط حرارتی همفشار و تراکم پذیری همدما
به طور تصادفی، با گرم کردن یک دماسنج اتانولی، به حد نهایی آن در لوله مویین دماسنج رسیدهایم. اگر ده درجه سانتیگراد دیگر، دماسنج را حرارت بدهیم، فشار لوله مویین چقدر افزایش پیدا میکند. اطلاعات مساله در زیر آورده شدهاند:
- $$\beta _ {glass} = 2.00 \times 10 ^ {-5} (^ \circ C)^ {-1}$$
- $$\beta _ {ethanol} = 11.2 \times 10 ^ {-4} (^ \circ C)^ {-1}$$
- $$\kappa _ {ethanol} = 11 \times 10 ^ {-5} (bar)^ {-1}$$
برای سادهسازی روابط نیز میتوانید از معادلات زیر کمک بگیرید:
$$\begin {equation}V \left (T _ { 2 } \right ) = V \left ( T _ {1} \right ) \left ( 1 + \beta \left [T _ {2} -T _ { 1 } \right ] \right ) \end {equation}$$
$$ln (1 + x) \approx x \ if \ x<<1$$
به کمک رابطه قبل خواهیم داشت:
$$\begin {equation} \begin {aligned}
\Delta P & = \int \frac { \beta_ {\text {ethanol}}} {\kappa} d T -\int \frac {1} {\kappa V} d V \approx \frac {\beta _ {\text {ethanol} }} {\kappa} \Delta T - \frac{1} {\kappa} \ln \frac {V_ {f}} {V_ {i}} \\
&=\frac {\beta _ {\text {ethanol}}} {\kappa} \Delta T - \frac{1}{\kappa} \ln \frac {V_{i} \left (1+ \beta _ {\text {glass}} \Delta T \right) } {V_ {i}} \approx \frac {\beta _ {\text {ethanol}}}{\kappa} \Delta T -\frac{1} { \kappa} \frac {V_{ i} \beta _{\text {glass}} \Delta T} { V_ {i}} \\
&= \frac {\left (\beta_ {\text {ethanol}} -\beta _{\text {glass}} \right)} {\kappa} \Delta T \\
&= \frac {(11.2-0.200) \times 10^ {-4} \left (^{ \circ} \mathrm {C}\right) ^ {-1}} {11.0 \times 10^ {-5}(\mathrm {bar}) ^ {-1}} \times 10.0 ^ {\circ} \mathrm {C}= 100 . \mathrm {bar}
\end {aligned} \end {equation}$$
با توجه به این جواب، به نظر نمیرسد که دماسنج، توانایی تحمل چنین فشاری را داشته باشد.

وابستگی انرژی درونی به دما و حجم در بررسی توابع حالت
در ادامه این بخش قصد داریم به کمک دیفرانسیل کامل بودن $$dU$$، تغییرات U با Tو V را نشان دهیم. برای یک ماده خالص، یا مخلوطی با ترکیب درصد ثابت، U یه کمک دو متغیر از سه متغیر فشار، حجم و دما تعیین میشود. از متغیرهای مختلفی میتوان استفاده کرد اما ما قصد داریم تا در این قسمت از متغیرهای دما و حجم استفاده کنیم. از آنجایی که U جزوی از توابع حالت به شمار میآید، تغییر دیفرانسیلی U را به شکل زیر نشان میدهیم:
$$\begin {equation} d U = \left ( \frac {\partial U } {\partial T } \right) _ {V} d T + \left ( \frac {\partial U } {\partial V } \right ) _ { T } d V \end {equation}$$
این رابطه بیان میکند که اگر T و V به مقدار $$T+dT$$ و $$V + dV$$ تغییر کنند، تغییرات $$U$$ به شکل $$du$$ خواهد بود که به شکل زیر مشخص میشوند. شیب $$U (T , V)$$ را نسبت به T و V میسنجیم و آنها را در مقادیر $$dT$$ و $$dV$$ ضرب میکنیم. تا زمانی که $$dT$$ و $$dV$$ را به صورت مقادیر دیفرانسیلی و بسیار کوچک داشته باشیم، از مشتقهای مرتبه بالاتر میتوان صرف نظر کرد. برای بدست آوردن عبارت سمت راست معادله بالا، از ترکیب این معادله با قانون اول ترمودینامیک و کار حجم-فشار بهره میگیریم.
$$\begin {equation} \require {cancel} \cancel {d q} - P_ {\text {external}} d V = \left ( \frac {\partial U } {\partial T} \right) _{V} d T +\left (\frac {\partial U} {\partial V} \right) _ {T} d V \end {equation}$$
در ابتدا، حالت همحجم را در نظر میگیریم که در آن، $$dV = 0$$ خواهد بود. در نتیجه، رابطه بالا به شکل زیر تغییر پیدا میکند:
$$\begin {equation} \require {cancel} \cancel {d q} = \left ( \frac {\partial U } {\partial T} \right) _{V} d T\end {equation}$$
توجه داشته باشید که طرف راست رابطه بالا، حاصلضرب توابع حالت و یک دیفرانسیل کامل است. بنابراین، $$ \cancel {d q}$$، رفتاری همچون یک تابع حالت خواهد داشت اما این مورد تنها زمانی اتفاق میافتد که مسیر (حجم ثابت) مشخص شده باشد. بنابراین، مقدار $$ \cancel {d q}$$ جزو توابع حالت به شمار نمیآید. با وجود اینکه عبارت $$( \frac {\partial U } {\partial T}) _{V} $$ کمی ناملموس به نظر میآید، اما به سادگی قابل اندازهگیری است.
به طور مثال، فرض کنید محفظهای مستحکم با دیوارههای عبور دهنده گرما (دیاترمال) را در یک حمام آبی غوطهور کرده باشیم. در این شرایط، محتوای موجود در محفظه به عنوان سیستم در نظر گرفته میشود. فرآیندی همچون یک واکنش شیمیایی، درون محفظه انجام و گرمای وارد شده به محیط، اندازهگیری میشود.در صورتیکه جریان $$ \cancel {d q}$$ داشته باشیم، افزایش یا کاهش $$dT$$ در سیستم و محیط مشاهده میشود که این افزایش و کاهش دما در سیستم و محیط، قابل اندازهگیری است. نسبت $$ \cancel {d q} / dT$$، نوع خاصی از ظرفیت حرارتی به شمار میآید که رابطه آنرا در زیر مشاهده میکنید:
$$\begin{equation}\frac{\cancel {d} q_{V}}{d T}=\left(\frac{\partial U}{\partial T}\right)_{V}=C_{V}\end{equation}$$
در این رابطه، $$ \cancel {d q} / dT$$، متناظر با مسیر همحجم و موسوم به ظرفیت حرارتی در حجم ثابت است. $$C_v$$ از جمله مقادیر با خواص مقداری به شمار میآید که به اندازه سیستم بستگی دارد. حال که $$C_v$$ را تعریف کردیم، میتوانیم به صورت آزمایشگاهی، تغییرات U با T در حجم ثابت را برای سیستمی با شرایط ذکر شده، حساب کنیم. این شرایط شامل سیستم با مواد خالص و مخلوط با ترکیب درصد ثابت در غیاب واکنش شیمیایی یا تغییر فاز است. بعد از اینکه $$C_v$$، انتگرال زیر را خواهیم داشت:
$$\begin {equation} \Delta U _ { V } = \int_ {T_{1}} ^ {T_{2}} C _{V} d T = n \int _{ T_{1}} ^ { T_{2}} C _ {V , m} d T \end {equation}$$
اگر بازه تغییرات دمایی محدودی داشته باشیم، $$C _ {V , m}$$ را میتوان به صورت ثابت در نظر گرفت. در چنین شرایطی، رابطه بالا به شکل زیر ساده خواهد شد:
$$\begin {equation} \Delta U _ {V} = \int _ { T_{1}} ^ { T_{2}} C _{V} d T= C_ {V} \Delta T = n C _ {V, m} \Delta T \end {equation}$$
این رابطه را به دو شکل زیر میتوان نوشت تا به طور صریح، رابطه $$q_v$$ و $$\Delta U$$ نشان داده شود:
$$\begin{equation} \int _ {i} ^{f} d q _ {V}= \int _ {i}^ {f} \left ( \frac {\partial U} {\partial T } \right ) _ {V} d T \\ q _ {V} = \Delta U \end {equation}$$
با وجود اینکه $$\cancel {d} q $$، یک دیفرانسیل کامل نیست، درصورتیکه مسیر (در اینجا حجم ثابت) تعیین شود، جواب انتگرال، مقدار منحصر به فردی خواهد داشت. رابطه بالا نشان میدهد که $$\Delta U$$ را برای یک فرآیند که در سیستم بسته با کار PV، میتوان از طریق اندازه گیری q در حجم ثابت، تعیین کرد.
وابستگی انرژی درونی به حجم در بررسی توابع حالت
حال، وابستگی U به V در دمای ثابت یعنی $$(\frac{\partial U}{\partial V})_ T$$ را در نظر بگیرید. واحد این کمیت، به شکل زیر نشان داده میشود و موسوم به «فشار داخلی» (Internal Pressure) است:
فشار = سطح/نیرو $$\begin{equation}\mathrm{J} / \mathrm{m}^{3}=(\mathrm{J} / \mathrm{m}) / \mathrm{m}^{2}=\mathrm{kg} \mathrm{ms}^{-2} / \mathrm{m}^{2}=\end{equation}$$
برای اینکه به طور صریح، فشار داخلی را بری مواد مختلف بدست بیاوریم، از رابطه زیر استفاده میکنیم که حاصل قانون دوم ترمودینامیک است:
$$\begin {equation} \left ( \frac { \partial U } { \partial V } \right) _{T} = T \left (\frac {\partial P } {\partial T } \right ) _ {V}-P \end {equation}$$
با استفاده از رابطه بالا، دیفرانسیل کل انرژی درونی را به شکل زیر خواهیم نوشت:
$$\begin {equation} d U= d U _ {V } + d U_ {T} = C _ {V} d T +\left [T\left (\frac {\partial P} {\partial T} \right ) _{V} - P \right] d V \end {equation}$$
در رابطه بالا از نمادهای $$d U _ {V }$$ و $$d U _ {V }$$ استفاده شده است که زیروندها بیانگر کمیت ثابت هستند. رابطه بالا، معادله مهمی به شمار میآید که در سیستمهای شامل گازها، مایعات و جامدات تکفاز یا مخلوط با ترکیب درصد یکسان بکار گرفته میشوند که در این سیستمها واکنشی شیمیایی یا تغییر فاز صورت نمیگیرد. البته به یاد دارید که پیشتر، $$dU$$ را به شکل دیگری نوشتیم. از مزایای نوشتن $$dU$$ به این شکل این است که عبارت $$ \left ( \frac { \partial U } { \partial V } \right) _{T}$$ را میتوان بر اساس متغیرهای سیتم یعنی فشار، حجم و دما به همراه مشتقهای این متغیرها تعیین کرد که همگی این مقادیر به طور آزمایشگاهی در دسترس هستند.
زمانی که $$ \left ( \frac { \partial U } { \partial V } \right) _{T}$$ و $$ \left ( \frac { \partial U } { \partial T } \right) _{V}$$ مشخص شدند، از این کمیتها برای تعیین $$dU$$ بکار گرفته میشوند. با توجه به اینکه U از جمله توابع حالت به شمار میآید، مسیر بین حالت اولیه و نهایی، اهمیتی ندارد. در تصویر زیر، سه مسیر متفاوت نشان داده شده که $$dU$$ برای تمامی این مسیرها یکسان است. برای سادهسازی محاسبات، مسیر انتخابی شامل دو بخش خواهد بود که در هرکدام، تنها یک متغیر تغییر میکند. نمونهای از این مسیر را میتوان به شکل زیر در نظر گرفت:
$$\begin {equation} V _ {i}, T_ {i} \rightarrow V_ {f}, T_ {i} \rightarrow V_ {f}, T _{f} \end {equation}$$
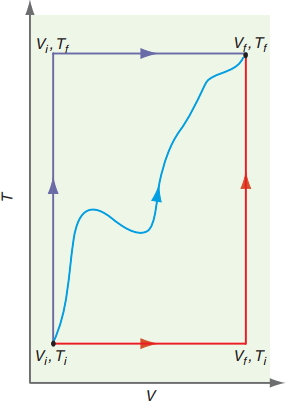
در بخش اول، با توجه به ثابت بودن دما خواهیم داشت:
$$\begin {equation} d U = d U_ {T} = \left [T \left (\frac {\partial P } { \partial T } \right ) _ { V } -P \right] d V \end {equation}$$
همچنین، در بخش دوم، حجم ثابت خواهد بود که خواهیم داشت:
$$d U = d U _ v = C_ vdT$$
در نهایت، تغییر کلی U برابر با مجموع تغییرات در این دو بخش خواهد بود:
$$d U _ {total} = d U _ v + d U _ T$$
بررسی وابستگی انرژی درونی به هر دو عامل دما و حجم
در مباحث قبلی مجله فرادرس نشان دادیم که در گازهای ایدهآل، $$U$$ به تنهایی تابعی از $$T$$ است. چنین اظهار نظری برای گازهای واقعی، مایعات و جامدات صحیح نیست زیرا تغییرات $$U$$ با حجم نیز باید در نظر گرفته شود. حال این سوال مطرح میشود که دما یا حجم، کدامیک در بررسی توابع حالت و تعیین $$\Delta U$$ فرآیند مورد نظر، تاثیر بیشتری دارند. برای پاسخ به این سوال، باید سیستمهایی به طور مجزا شامل یک گاز ایدهآل، گاز واقعی، مایع و جامد در نظر گرفته شوند. مثال زیر نشان میدهد رابطه قبل برای انرژی درونی، به هنگام بهرهگیری از گاز ایدهآل، به شکل سادهتری تبدیل میشود.
مثال برای اثبات رابطه انرژی درونی و گاز ایده آل
مقدار $$\left ( \frac { \partial U } { \partial V } \right) _{T}$$ برای یک گاز ایدهآل را بدست آورید و رابطهای به کمک معادله $$\begin {equation} d U= d U _ {V } + d U_ {T} = C _ {V} d T +\left [T\left (\frac {\partial P} {\partial T} \right ) _{V} - P \right] d V \end {equation}$$ برای گاز ایدهآل بدست آورید.
$$\begin {equation} \left (\frac {\partial U } { \partial V } \right ) _{T} = T \left ( \frac {\partial P } {\partial T }\right ) _ {V}- P = T \left ( \frac {\partial [n R T / V] } {\partial T} \right ) _ {V} -P = \frac {n R T} { V} - P = 0 \end {equation}$$
بنابراین، $$dU = C_ v dT$$ که نشان میدهد به هنگام بررسی توابع حالت برای یک گاز ایدهآل، انرژی درونی تابعی از دما است.
تغییرات انرژی درونی برای گاز واقعی در بررسی توابع حالت
همانطور که در مثال قبل مشاهده کردید، انرژی درونی برای گاز ایدهآل، تنها به دما وابسته است و به طور ویژه، وابستگی به حجم ندارد. با توجه به اینکه مولکولهای گاز ایدهآل یکدیگر را جذب یا دفع نمیکنند، هیچ انرژی برای تغییر فاصله متوسط بین مولکولها (افزایش یا کاهش حجم) نیاز نخواهیم داشت:
$$\begin {equation} \Delta U = \int _ { T _ { i}} ^{ T_{ f}} C _{V} (T) d T \end {equation}$$
به یاد داشته باشید، با توجه به اینکه $$U$$ تنها تابعی از دما است، رابطه بالا، برای یک گاز ایدهآل، حتی در صورت ثابت نبودن حجم نیز صدق میکند. حال، تغییرات انرژی درونی در اثر دما و حجم را برای یک گاز واقعی در نظر بگیرید. روش آزمایشگاهی برای تعیین $$\left ( \frac { \partial U } { \partial V } \right) _{T}$$ را «جیمز ژول» به کمک دستگاهی شامل دو بالون شیشهای ارائه داد. این دو بالون توسط یک شیر به یکدیگر متصل شده و هردو، داخل یک حمام آبی، غوطهور شدهاند.
در تصویر زیر، یک مدل ایدهآل از این دستگاه را مشاهده میکنید. زمانی که شیر بین دو محفظه باز شود، گاز در حجم A، انبساط پیدا خواهد کرد تا حجم A+B را پر کند. در توصیف نتایج این آزمایش، باید فهم صحیحی از مرز بین سیستم و محیط داشته باشیم. در اینجا، مرز سیستم را به گونهای در نظر گرفتیم که شامل کل گاز باشد.
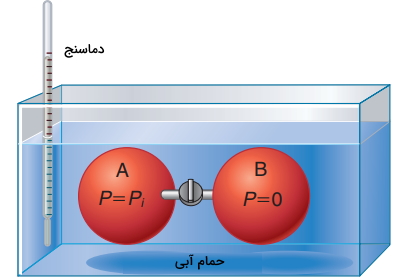
در حالت اولیه، مرز، تنها شامل $$V_A$$ خواهد بود اما در طول انبساط، این حجم حرکت میکند تا مولکولهای گاز را هم شامل شود. با این انتخاب، حجم سیستم از $$V_A$$ قبل از انبساط به $$V _ A + V_ B$$ بعد از انبساط تغییر میکند. بر اساس قانون اول ترمودینامیک خواهیم داشت:
$$\begin{equation}\require {cancel} \cancel {d} q - P _ {\text {external}} d V = \left (\frac {\partial U } {\partial T} \right ) _{V} d T +\left (\frac {\partial U } {\partial V } \right) _ {T} d V \end {equation}$$
سیستم، شامل تمامی گاز است و بنابراین، فشار خارجی برابر با صفر خواهد بود زیرا فشاری در اثر خلا نخواهیم داشت. بنابراین، رابطه بالا به شکل زیر ساده میشود:
$$\begin{equation}\require {cancel} \cancel {d} q= \left (\frac {\partial U } {\partial T} \right ) _{V} d T +\left (\frac {\partial U } {\partial V } \right) _ {T} d V \end {equation}$$
بمنظور رسیدن به دقت آزمایشگاهی، ژول دریافت که $$dT$$ محیط باید صفر باشد. از آنجایی که حمام آبی و سیستم در تعادل گرمایی با یکدیگر قرار دارند، $$dT$$ برابر با $$dT$$ محیط و صفر خواهد بود. بنابراین، رابطه بالا به صورت زیر ساده میشود:
$$\begin{equation}\left (\frac {\partial U } {\partial V } \right) _ {T} d V = 0 \end {equation}$$
با توجه به اینکه $$d V \neq 0$$، ژول به این نتیجه رسید که عبارت $$\begin{equation}\left (\frac {\partial U } {\partial V } \right) _ {T} \end {equation}$$ برابر با صفر خواهد بود. آزمایش ژول، اعتبار چندانی نداشت زیرا حساسیت آزمایشگاهی آن محدود بود که در مثال زیر به آن پرداخته شده است.
مثال برای نقاط ضعف آزمایش ژول در بررسی توابع حالت
در آزمایش ژول برای تعیین $$(\frac{\partial U} {\partial V}) _ T$$، ظرفیت حرارتی در گاز و حمام آبی محیط به صورت رابطه زیر به یکدیگر مرتبط شده بودند:
$$C _ {Surrounding} / C _ {System} \approx 1000$$
اگر دقت اندازهگیری دمای محیط، برابر با $$\pm 0.006\ ^ \circ C$$ باشد، حداقل تغییر در دمای گاز، چه میزان خواهد بود؟
دستگاه آزمایش را به صورت دو سیستم کنشگر در یک محفظه آدیاباتیک در نظر میگیریم. اولین سیستم، حجم محفظههای A و B و دومین سیستم، حمام آبی و محفظهها است. با توجه به اینکه این دو سیستم، به صورت عایق قرار دارند، خواهیم داشت:
$$\begin {equation} \begin {aligned}
q & = C _{\text {water bath} } \Delta T _{\text {water bath} } + C _{\text {gas}} \Delta T _{\text {gas}}= 0 \\
\Delta T _ {\text {gas}} & = -\frac {C _{\text {water bath}}}{C _{\text {gas}}} \Delta T _{\text {water bath}} = -1000 \times \left ( \pm 0.006 ^ {\circ} \mathrm {C} \right ) = \mp 6 ^ {\circ} \mathrm {C}
\end {aligned} \end {equation}$$
در این محاسبات، $$\Delta T _{\text {gas}}$$، تغییرات دمایی گاز است که در اثر انبساط سبب میشود تا به تعادل گرمایی با حمام آبی برسد. علامت این تغییرات، در طول انبساط، منفی است. با توجه به این که حداقل دمای قابل شناسایی، مقدار بزرگی است، چنین دستگاهی به طور واضح برای اندازهگیری تغییرات کوچک دما در اثر انبساط، مناسب نخواهد بود.