قانون پایستگی انرژی چیست؟ – اصل بقای انرژی به زبان ساده

به احتمال قوی بارها در زندگی یا در دوران تحصیل خود این عبارت را شنیده‌اید «مقدار انرژی موجود در جهان ثابت است و تغییر نمی‌کند». این جمله بیان‌گر یکی از مهم‌ترین قانون‌های موجود در فیزیک به نام قانون پایستگی انرژی یا قانون بقای انرژی است. در این مطلب، با این قانون به زبان ساده همراه با حل مثال‌های گوناگون آشنا می‌شویم.

قانون پایستگی انرژی چیست ؟

مقدار انرژی موجود در جهان ثابت است. انرژی نه از بین می‌رود، نه به وجود می‌آید، بلکه از شکلی به شکل دیگر تبدیل می‌شود. به بیان دیگر:

مقدار انرژی در هر فرآیندی ثابت است. شکل آن ممکن است تغییر کند یا از سیستمی به سیستم دیگر منتقل شود، اما مقدار آن همواره ثابت خواهد بود. 

برای تعریف قانون پایستگی انرژی از عبارت ثابت و پایسته استفاده کردیم. در فیزیک، به هر کمیت فیزیکی مشخصی (قابل اندازه‌گیری باشد) که با گذشت زمان در سیستم بسته‌ای تغییر نکند، کمیت پایسته گفته می‌شود. به عنوان مثال، خط‌کش انعطاف‌پذیری با طول بیست سانتی‌متر را در نظر بگیرید. اکنون خط‌کش را از دو طرف خم کنید و دوباره آن‌ را به حالت اول بازگردانید. طول آن را دوباره اندازه می‌گیریم و مقدار ۲۰ سانتی‌متر را به دست می‌آوریم. در نتیجه، طول خط‌کش قبل و بعد از خم کردن، ثابت مانده است. به عبارت دیگر، مقدار طول خط‌کش پایسته است.

کمیت‌های پایسته زیادی در فیزیک وجود دارند. این کمیت‌های پایسته برای پیش‌بینی پدیده‌های فیزیکی بسیار لازم هستند. در علم فیزیک، سه کمیت بنیادی، پایسته و ثابت هستند:

1. انرژی
2. تکانه
3. تکانه زاویه‌ای

ذکر این نکته مهم است که انرژی در سیستم‌های بسته یا ایزوله پایسته است. اما توجه به دو نکته زیر بسیار مهم است:

1. منظور از انرژی، انرژی کل سیستم است. شکل انرژی اجسام متحرک در اطرافمان به طور پیوسته تغییر می‌کند. اما، مقدار کل آن همواره ثابت است.
2. قانون پایستگی انرژی تنها در سیستم‌های بسته و ایزوله اعمال می‌شود. توپی که بر روی زمین زبری حرکت می‌کند، از قانون بقای انرژی پیروی نخواهد کرد. زیرا توپ نسبت به سطح زمین ایزوله نشده است. در حقیقت، زمین بر روی توپ از طریق نیروی اصطکاک کار انجام داده است. اگر توپ و زمین را با هم در نظر بگیریم، قانون پایستگی انرژی برقرار خواهد بود. به مجموعه توپ+زمین در این حالت سیستم گفته می‌شود.

در فیزیک مکانیک با سیستم‌هایی برخورد می‌کنیم که انرژی جنبشی، انرژي پتانسیل گرانشی، انرژی کشسانی فنر و انرژی گرمایی دارند. در ادامه، در مورد حل مساله با استفاده از قانون بقای انرژی توضیح داده خواهد شد.

سیستم چیست ؟

در فیزیک، سیستم به مجموعه‌ای از اشیاء گفته می‌شود که اثرات فیزیکی همچون نیرو روی آن‌ها بررسی می‌شود. اگر می‌خواهیم حرکت جسمی را با استفاده از قانون پایستگی انرژی توضیح دهیم، باید سیستم را به گونه‌ای انتخاب کنیم که جسم موردنظر و تمام اجسامی که با آن برهم‌کنش دارند را در بر بگیرد.

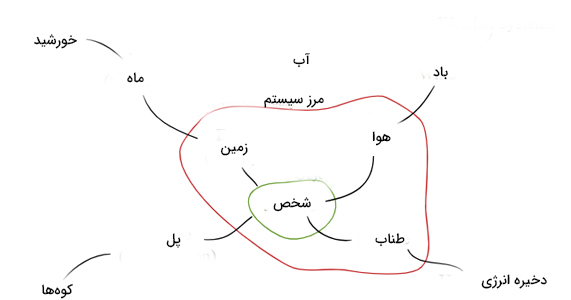
در عمل، همواره از بعضی از برهم‌کنش‌های وارد شده بر جسم چشم‌پوشی می‌کنیم. به هنگام تعریف سیستم، باید آن را به وسیله خط یا منحنی از محیط اطرافش جدا کنیم. با نادیده گرفتن محیط اطراف، دقت محاسبات کاهش خواهد یافت. اما تحلیل مسائل راحت‌تر می‌شود.

شخصی را در نظر بگیرید که به ورزش بانجی جامپینگ علاقه بسیار زیادی دارد. او از روی پلی می‌پرد. در پایین‌ترین نقطه، سیستم از شخص، کش متصل به پای او و زمین تشکیل شده است. اگر بخواهیم مسئله را با دقت بیشتری حل کنیم، باید هوا را نیز به عنوان بخشی از سیستم در نظر بگیریم. هوا بر روی فرد از طریق نیروی مقاومت کار انجام می‌دهد. حتی می‌توانیم جلوتر برویم و پل را نیز در سیستم انتخابی در نظر بگیریم. اما از آنجایی که وزن پل از وزن فرد بسیار سنگین‌تر است، به راحتی می‌توانیم آن را نادیده بگیریم. همچنین، می‌دانیم طراحی پل به گونه‌ای انجام شده است که پرش فرد تاثیر زیادی بر روی آن نخواهد گذاشت.

مثال‌ های قانون پایستگی انرژی

انرژی توانایی انجام کار است. بر طبق قانون بقای انرژی، انرژی نه از بین می‌رود و نه به وجود می‌آید، بلکه تنها از صورتی به صورت دیگر تبدیل می‌شود. این جمله بدان معنا است که اتلاف در شکلی از انرژی سبب افزایش شکل دیگری از انرژی خواهد شد. قانون پایستگی انرژی را در بسیاری از فعالیت‌های روزمره مشاهده می‌کنیم.

لامپ روشنایی

هنگامی که کلید لامپ را روشن می‌کنیم، اتصال الکتریکی بین منبع تغذیه الکتریکی و لامپ برقرار می‌شود. با انتقال جریان الکتریکی در مدار الکتریکی بسته‌ای، لامپ روشن خواهد شد. در اینجا، انرژی الکتریکی به انرژی نورانی لامپ تبدیل می‌شود. بنابراین، لامپ روشنایی یکی از واضح‌ترین مثال‌های قانون بقای انرژی است. اما سوالی که ممکن است مطرح شود آن است که آیا تمام انرژی الکتریکی به نورانی تبدیل می‌شود؟ پاسخ به این پرسش خیر است.

اگر پس از گذشت مدت زمانی به لامپ دست بزنیم، دستمان خواهد سوخت. در نتیجه، مقداری از انرژی الکتریکی ورودی به لامپ به انرژی گرمایی تبدیل خواهد شد.

برخورد

جسم متحرکی به جسم ساکنی برخورد می‌کند. جسم ساکن پس از برخورد با جسم متحرک شروع به حرکت خواهد کرد. دلیل این امر آن است که انرژی جنبشی جسم متحرک از بین نمی‌رود بلکه مقداری از آن به جسم ساکن منتقل می‌شود.

سقوط جسم از ارتفاع

جسمی که در ارتفاع مشخصی از سطح زمین قرار گرفته دارای انرژی پتانسیل گرانشی است. هنگامی که جسم در اثر کشش جاذبه زمین سقوط می‌کند، انرژی پتانسیل ذخیره شده در آن به انرژی جنبشی تبدیل می‌شود. به هنگام رسیدن جسم به سطح زمین، انرژی پتانسیل آن صفر، و انرژی جنبشی آن بیشینه خواهد بود.

سوختن چوب

انرژی پتانسیل در چوب یا دیگر منابع سوختی ذخیره شده است. به هنگام سوختن چوب، انرژی شیمیایی ذخیره شده در آن به انرژی گرمایی و نورانی تبدیل می‌شود. در هنگام سوختن چوب، انرژی از بین نمی‌رود و به وجود نمی‌آید. در نتیجه، قانون بقای انرژی به هنگام سوختن چوب برقرار است.

طبل زدن

به هنگام نواختن طبل، انرژی مکانیکی به انرژی صوتی تبدیل می‌شود. در اینجا نیز انرژی از بین نمی‌رود و به وجود نمی‌آید بلکه از حالتی به حالت دیگر تبدیل خواهد شد.

باتری

انرژی تولید شده در باتری نتیجه قانون بقای انرژی است. مواد شیمیایی موجود در باتری پس از گذراندن تعدادی واکش‌های شیمیایی، انرژی شیمیایی تولید می‌کنند. این انرژی شیمیایی به انرژی الکتریکی تبدیل می‌شود. انرژی الکتریکی تولید شده می‌تواند به دیگر صورت‌های انرژی مانند صوتی یا گرمایی تبدیل شود. در نتیجه، در باتری نیز انرژی از بین نخواهد رفت.

جویدن غذا

برای جویدن و خوردن غذا به انرژی مکانیکی نیاز داریم. غذا پس از انجام واکنش‌های شیمیایی لازم به صورت انرژی شیمیایی در بدن ذخیره می‌شود. این انرژی شیمیایی به هنگام انجام فعالیت‌های روزانه به صورت‌های دیگر انرژی تبدیل خواهد شد.

آونگ

هنگامی که آونگ از پایین‌ترین نقطه خود به سمت بالا حرکت می‌کند، انرژی جنبشی به انرژی پتانسیل گرانشی تبدیل می‌شود. به هنگام حرکت آونگ به سمت پایین، انرژی پتانسیل گرانشی به انرژی جنبشی تبدیل خواهد شد.

قانون بقای انرژی مکانیکی چیست ؟

انرژی مکانیکی سیستم منزوی همواره ثابت است. پایستگی انرژی مکانیکی تنها هنگامی برقرار است که نیروهای وارد شده بر سیستم پایستار باشند.

$$E_1 = E_2$$

انرژی مکانیکی به صورت مجموع انرژی پتانسیل و انرژی جنبشی سیستم تعریف می‌شود:

$$E_M = E_p \ + \ E_k$$

ذکر این نکته مهم است که تنها نیروهای پایستار مانند نیروی کشش فنر و نیروی گرانش زمین انرژی پتانسیل دارند.

اگر نیروهای خارج از سیستم یا نیروهای غیرپایستار بر روی آن کار انجام دهند، انرژی مکانیکی سیستم ثابت نخواهد بود. در این حالت، تغییرات انرژی مکانیکی برابر با کار انجام شده از طرف نیروهای پایستار است:

$$W = \triangle E$$

به هنگام حل مسائل مربوط به پایستگی انرژی مکانیکی گام‌های زیر را به ترتیب طی می‌کنیم:

1. سیستم مورد مطالعه را مشخص کنید. به طور معمول، به هنگام استفاده از قانون پایستگی انرژی مکانیکی، سیستم مورد نظر بیشتر از یک جسم دارد.
2. نیروهای وارد بر جسم یا اجسام را تعیین کنید.
3. پاسخ به این سوال: آیا نیروهای پایستار بر روی سیستم کار انجام می‌دهند یا نیروهای غیرپایستار. اگر نیروی غیرپایستاری مانند نیروی اصطکاک بر روی سیستم کار انجام دهد، آن‌گاه انرژی مکانیکی پایسته نیست.
4. برای هر نیرویی که کار انجام می‌دهد، نقطه‌ مرجعی را انتخاب کنید. سپس انرژی پتانسیل مربوط به آن نیرو را به دست آورید. نقاط مبدا برای انرژی‌های پتانسیل مختلف می‌توانند یکسان یا غیریکسان باشند.
5. قانون پایستگی انرژی مکانیکی را در هر نقطه دلخواه بنویسید.

مثال اول قانون بقای انرژی مکانیکی

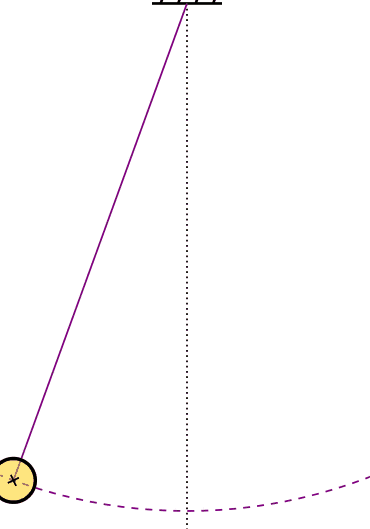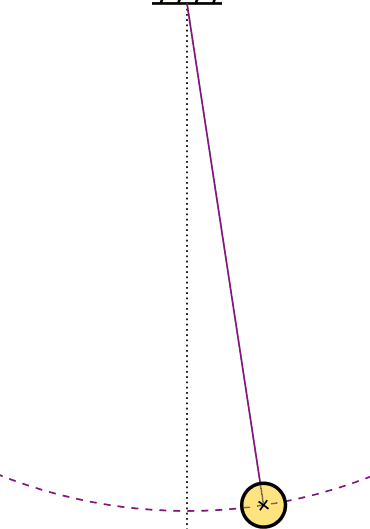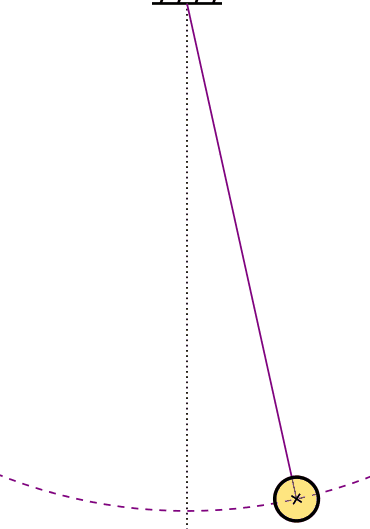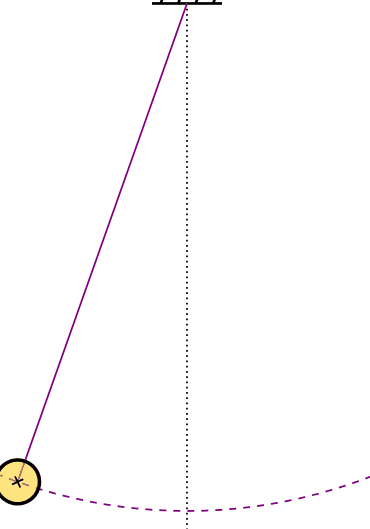
ذره‌ای به جرم m به نخ بدون جرمی به طول یک متر وصل شده است (تصویر نشان داده شده در ادامه). هنگامی که زاویه بین نخ و خط عمودی گذرنده از نقطه اتصال نخ برابر ۳۰ درجه است، ذره از حالت سکون رها می‌شود. سرعت ذره را هنگامی که به پایین‌ترین نقطه کمان می‌رسد به دست آورید.

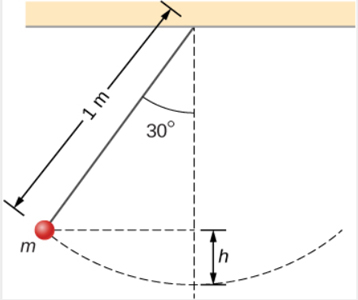
پاسخ:

در ابتدا، سیستم مورد نظر را انتخاب می‌کنیم. مجموعه ذره و زمین را به عنوان سیستم در نظر می‌گیریم. تنها نیروی وارد بر ذره نیروی جاذبه گرانش و از نوع نیروی پایستار است. نیروی مقاومت هوا را نادیده می‌گیریم. همچنین، کار انجام شده از طرف نیروی نخ برابر صفر است. زیرا این نیرو بر مسیر حرکت ذره عمود است. بنابراین، انرژی مکانیکی سیستم پایسته است.

$$E_1 = E_2\ \\\triangle E= 0$$

از آنجایی که ذره از حالت سکون شروع به حرکت کرده است، انرژی جنبشی اولیه آن برابر صفر خواهد بود. در گام بعدی نقطه مرجع را در پایین‌ترین نقطه کمان انتخاب می‌کنیم.

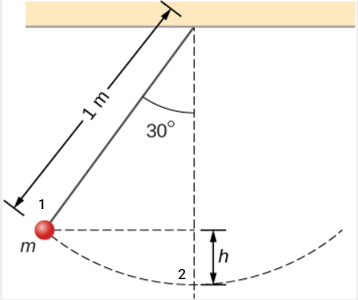
نیروهای غیرپایستار را نادیده می‌گیریم. قانون پایستگی انرژی را بین نقطه ۱ و ۲ به صورت زیر می‌نویسیم:

$$K_1 + U_1 = K_2 + U_2$$

ذره از نقطه ۱ رها می‌شود. بنابراین سرعت اولیه و در نتیجه انرژی جنبشی اولیه آن برابر صفر خواهد بود. در نقطه ۲، انرژی پتانسیل را صفر در نظر می‌گیریم. بنابراین داریم:

$$0 + mgh = \frac{1}{2} m v^2 +0 \\ v = \sqrt{2gh}$$

مقدار ارتفاع h داده نشده است. با استفاده از مثلثات مقدار آن به دست خواهد آمد.

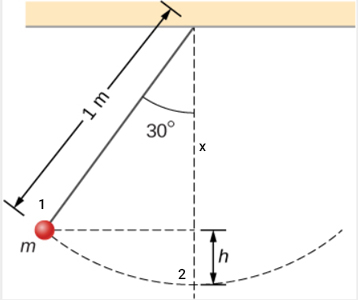
$$cos \theta = \frac{x}{L} , sin\theta = Lcos\theta$$

ارتفاع h به صورت زیر به دست خواهد آمد:

$$x + h = L\\ Lcos\theta + h = L \\ h = L-Lcos\theta = L(1-cos\theta)$$

با جایگزینی داده‌های مثال داریم:

$$v=\sqrt{2gL(1 - cos\theta} = \sqrt{2 (9.8 \frac{m}{s^2}) (1 m) (1 - cos30^o)} = 1.62 \ \frac{m}{s}$$

مثال دوم قانون پایستگی انرژی مکانیکی

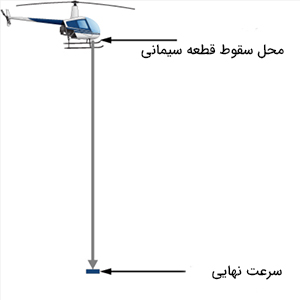
هلیکوپتری در ارتفاع یک کیلومتری از سطح زمین قرار دارد. در این هنگام قطعه‌ای سیمانی به وزن ۱۵ کیلوگرم از هلیکوپتر به سمت زمین سقوط و با سرعتی برابر با ۴۵ متر بر ثانیه به زمین برخورد می‌کند. چه مقدار انرژی مکانیکی در مدت سقوط قطعه تلف خواهد شد؟

پاسخ:

جسم مورد مطالعه قطعه سیمانی است. نیروهای وارد شده بر قطعه دو نیروی گرانش زمین و مقاومت هوا هستند. نیروی وزن، نیروی پایستار است. اما نیروی غیرپایستار مقاومت هوا بر روی قطعه کار منفی انجام می‌دهد. در نتیجه، مقدار نیروی تلف شده در مسیر سقوط برابر با مقدار کار انجام شده است:

$$\triangle E _{diss} =|W| =|\triangle (K+U)|$$

انرژی جنبشی قطعه سیمانی در نقطه رها شدن برابر صفر است. مقدار انرژی پتانسیل گرانشی را بر روی زمین برابر صفر قرار می‌دهیم.

مقدار انرژی مکانیکی تلف شده توسط مقاومت هوا برابر است با:

$$\triangle E_{diss} = |K_f-K+U_f-U_i| \\ =|\frac{1}{2}(15 \ kg)(45 \ \frac{m}{s} )^2-0 - 0 - (15 \ kg) ( 9.8 \ \frac{m}{s^2})(1000 \ m)| = 130 \ kJ$$

مثال سوم قانون بقای انرژی مکانیکی

گلوله برفی به جرم ۱/۵ کیلوگرم با زاویه ۳۴ درجه سانتی‌گراد نسبت به افق و با سرعت اولیه 20 متر بر ثانیه پرتاب می‌شود. (۱) انرژی جنبشی اولیه آن را به دست آورید. (۲) انرژی پتانسیل گرانشی سیستم گلوله برفی-زمین به هنکام رسیدن کلوله به بیشینه ارتفاع چه مقدار تغییر خواهد کرد؟ (۳)‌ ارتفاع بیشینه را به دست آورید.

پاسخ:

قسمت (۱): از آنجایی که سرعت اولیه گلوله برابر 20 متر بر ثانیه است، انرژی جنبشی اولیه آن برابر است با:

$$K_i = \frac{1}{2}m v_0^2 = \frac{1}{2} (1.50 \ kg) (20.0 \ \frac{m}{s})^2 = 300\ J$$

قسمت (۲): از آنجایی که گلوله برقی به صورت عمود بر سطح زمین پرتاب نشده است، پس از رسیدن به ارتفاع بیشینه سرعت آن غیر صفر خواهد بود. از این‌رو، مقدار انرژی جنبشی آن در ارتفاع بیشینه غیر صفر است.

در ارتفاع بیشینه، مولفه سرعت در راستای محور y برابر صفر است. اما از آنجایی که پرتابه شتاب افقی ندارد، در نتیجه مولفه سرعت در راستای x ثابت خواهد بود. بنابراین داریم:

$$v_{0x} = v_0cos\theta_{0}= (20.0 \frac{m}{s}) cos 34^o = 16.6 \ \frac{m}{s}$$

بنابراین، مقدار سرعت گلوله برفی در ارتفاع بیشینه برابر 16/6 متر بر ثانیه به دست آمد. مقدار انرژی جنبشی در ارتفاع بیشینه برابر است با:

$$K_f = \frac{1}{2}mv_f^2 = \frac{1}{2}(1.50 \ kg)(16.6 \frac{m}{s} )^2 = 206 \ J$$

در این مثال، تنها نیروهای پایستار‌ (مانند گرانش) وجود دارند. در نتیجه قانون بقای انرژی مکانیکی برقرار است:

$$K_i + U_i = K_f+U_f$$

مقدار انرژی جنبشی اولیه را برابر 300 ژول به دست آوردیم. مقدار انرژی پتانسیل گرانشی بر روی زمین برابر صفر است. بنابراین، انرژی پتانسیل گرانشی نهایی به صورت زیر به دست خواهد أمد:

$$U_f =K_i+U_i-K_f \\ = 300 \ J +0 - 206 \ J \\ = 94 \ J$$

قسمت (۳): اگر ارتفاع بیشینه را با ‌h نشان دهیم داریم:

$$U_f = mgh \\ h = \frac {U_f}{mg}= \frac {(94 \ J)} {(1.5 \ kg) (9.80 \frac {m}{m^2})} = 6.38 \ m$$

مثال چهارم قانون پایستگی انرژی مکانیکی

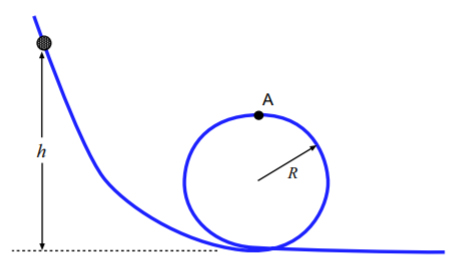
دانه تسبیح کوچکی بر روی مسیر بدون اصطکاکی به صورت نشان داده شده در تصویر زیر حرکت می‌کند. اگر دانه از ارتفاع h = 3/5R رها شود، سرعت آن در نقطه A چه مقدار است؟ اگر وزن دانه تسبیخ برابر 5/00 گرم باشد، اندازه نیروی عمودی سطح را به دست آورید.

پاسخ:

در این مثال هیچ نیروی اصطکاکی بر ذره وارد نمی‌شود. تنها نیروی وارد بر ذره نیروی پایستار وزن است. از طرف سطح نیروی عمودی N بر دانه تسبیح وارد می‌شود، اما این نیرو کاری بر روی ذره انجام نمی‌دهد. بنابراین، انرژی مکانیکی پایسته است.

دانه تسبیح از ارتفاع h رها می‌شود. در نتیجه، سرعت و انرژی جنبشی اولیه آن برابر صفر خواهد بود. اگر مقدار انرژی پتانسیل گرانشی بر روی سطح زمین را برابر صفر بگیریم، مقدار انرژی پتانسیل اولیه برابر است با:

$$U_i = mgh$$

در نقطه A، دانه تسبیح دارای انرژی جنبشی و پتانسیل است. اگر سرعت حرکت آن در نقطه A برابر v باشد، داریم:

$$K_f = \frac{1}{2}mv^2$$

در نقطه A ارتفاع از سطح زمین برابر 2R است. در نتیجه، انرژی پتانیل در این نقطه برابر $$U_f = mg(2R) = 2mgR$$ است. قانون بقای انرژی مکانیکی در این مثال برقرار است:

$$K_i + U_i = K_f+U_f$$

با جایگزینی مقادیر به دست آمده برای انرژی در نقاط اولیه و پایانی داریم:

$$0 + mgh = \frac{1}{2}mv^2 + 2mgR$$

با حذف m از طرفین رابطه بالا داریم:

$$gh = \frac{1}{2}v^2 +2gR \Rightarrow \frac{1}{2}v^2 = gh - rgR = g(h-2R) \\ v^2 = 2g(h-2R) = 2g(3.50R-2R) = 2g(1.50 R) = 3.5gR \\ v = \sqrt{3.0gR}$$

در قسمت بعدی، به نیروهای وارد شده بر دانه تسبیح در نقطه A توجه می‌کنیم. همان‌گونه که در تصویر مشاهده می‌کنید، نیروی وزن mg به سمت پایین بر دانه وارد می‌شود. همچنین، نیروی عمود بر سطح N نیز به سمت پایین بر ذره وارد می‌شود.

در نقطه ‌A دانه تسبیح در مسیر دایره‌ای به شعاع ‌R و با سرعت v حرکت می‌کند. بنابراین جهت شتاب آن به سمت مرکز دایره و رو به پایین است. می‌دانیم جمع نیروهای رو به پایین به ما شتاب مرکزگرا را می‌دهد.

$$mg+N=\frac{mv^2}{R} \Rightarrow \ N=\frac{mv^2}{R}-mg = m(\frac{v^2}{R}-g)$$

با جایگزینی رابطه به دست آمده برای سرعت داریم:

$$N=m(\frac{v^2}{R}-g)=m(\frac{3.0gR}{R}-g)=m(2g)=2mg \\ N=2 (5.00\times 10^{-3} \ kg)(9.80 \frac{m}{s^2})=9.80\times 10^{ \ -2}\ N$$

مثال پنجم قانون پایستگی انرژی مکانیکی

جعبه‌ای بر روی سطح شیب‌داری به ارتفاع ۱۵۰ متر و در حالت سکون قرار دارد. اگر این جعبه بر روی سطح شیب‌دار به سمت پایین حرکت کند، سرعت آن به هنگام رسیدن به پایین سطح چه مقدار است؟

پاسخ:

از آنجایی که تنها نیروهای وارد شده بر جعبه نیروی پایستار وزن است، در نتیجه قانون پایستگی انرژی مکانیکی برقرار است.

$$E_i = E_f$$

در نقطه شروع یا نقطه ‌A، انرژی جنبشی برابر صفر است زیرا جعبه از حالت سکون شروع به حرکت کرده است. در نقطه B که سطح زمین است، انرژی پتانسیل گرانشی برابر صفر است.

$$U= K$$

هنگامی که جعبه به سمت پایین سطح شیب‌دار حرکت می‌کند، انرژی پتانسیل گرانشی به انرژی جنبشی تبدیل می‌شود.

$$mgh = \frac{1}{2}mv^2 \\ 2gh = v^2$$

در نتیجه مقدار سرعت در نقطه B به صورت زیر به دست می‌آید:

$$v_B = \sqrt{2(9.8)(150\ m)}=54.22 \ \frac{m}{s}$$

مثال ششم قانون بقای انرژی مکانیکی

جعبه‌ای به جرم هشت کیلوگرم فنر افقی را به اندازه ۲/۵ سانتی‌متر فشرده کرده است ($$k=300 \frac{N}{m}$$). (۱) سرعت جعبه در لحظه جدا شدن از فنر چه مقدار است؟ (۲)‌ جعبه پس از جدا شدن از فنر تا چه ارتفاعی بالای تپه بالا می‌رود؟

پاسخ:

قسمت (۱): هنگامی که فنر فشرده است، سیستم جعبه-فنر دارای انرژی پتانسیل است. پس از رها شدن فنر، انرژی پتانسیل به انرژی جنبشی تبدیل می‌شود. از آنجایی که ارتفاع تغییری نمی‌کند، در نتیجه مقدار انرژی پتانسیل گرانشی برابر صفر است.

انرژی پتانسیل کشسانی فنر = انرژی جنبشی

$$\frac{1}{2}kx^2 = \frac{1}{2}mv^2$$

با جایگذاری مقادیر داده شده در رابطه بالا داریم:

$$(300)(2.5)^2 = 8v^2 \\ v= 15.31 \frac{m}{s}$$

قسمت (۲): در قسمت دوم، جعبه با سرعت ۱۵/۳۱ متر بر ثانیه از فنر جدا و تا ارتفاع h بر روی تپه بالا می‌رود.

$$\frac{1}{2}mv^2 = mg h \\ \frac{1}{2}(15.31)^2 = (9.8)h\\ h = 12 \ m$$

مثال هفتم قانون بقای انرژی مکانیکی

جعبه‌ای به جرم ۱۵ کیلوگرم با سرعت ۱۵ متر بر ثانیه به دیواری برخورد و به طور کامل متوقف می‌شود. چه مقدار انرژی گرمایی در هنگام برخورد تولید می‌شود؟

پاسخ:

جعبه پس از برخورد به دیوار به طور کامل می‌ایستد، سوالی که مطرح می‌شود آن است که انرژی جنبشی آن کجا رفته است. تمام انرژی جنبشی به انرژی گرمایی تبدیل شده است. در ابتدا انرژی جنبشی جعبه قبل از برخورد به دیوار را حساب می‌کنیم.

$$K=\frac{1}{2}mv^2 = \frac{1}{2}(12 \ kg) (15 \frac{m}{s})^2 = 6\times(225)= 1350 \ J$$

تمام این انرژی جنبشی به انرژی گرمایی تبدیل می‌شود.

مثال هشتم قانون بقای انرژی

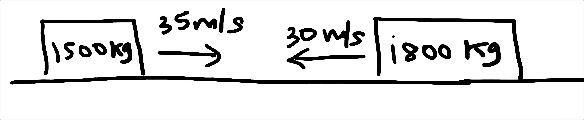
ماشینی به جرم 1۵00 کیلوگرم با سرعت 35 متر بر ثانیه به سمت شرق در حال حرکت است. ناگهان به اتومبیلی که با سرعت 30 متر بر ثانیه به سمت غرب در حال حرکت است برخورد می‌کند. هر دو ماشین پس از تصادف به طور کامل متوقف می‌شوند. چه مقدار انرژی گرمایی به هنگام برخورد تولید شده است؟

پاسخ:

در ابتدا انرژی جنبشی کل را به دست می‌آوریم:

انرژی جنبشی کل = انرژی جنبشی ماشین ۱ + انرژی جنبشی ماشین ۲

$$K=\frac{1}{2}mv_1^2 + \frac{1}{2}mv_2^2 \\ K=\frac{1}{2}[(1500)(35)^2 + (1800)(30)^2 \\ K=1728750 \ J$$

تمام انرژی جنبشی محاسبه شده پس از برخورد دو ماشین به انرژی گرمایی تبدیل خواهد شد. در نتیجه، به هنگام برخورد دو ماشین با یکدیگر مقدار زیادی انرژی گرمایی تولیدمی‌شود.

قانون بقای انرژی در ماشین آتوود

ماشین آتوود وسیله ساده‌ای در آزمایشگاه‌های فیزیک است که از قرقره، نخ و جرم‌های مختلف تشکیل شده است. نکته مهم در بیشتر ماشین‌های آتوود آن است که از جرم نخ عبوری از قرقره و متصل به جرم‌ها چشم‌پوشی می‌شود. در نتیجه، کشش نخ در سراسر نخ یکسان خواهد بود. قانون بقای انرژی در ماشین آتوود نیز یرقرار است. برای درک بهتر این موضوع، مثالی در ادامه حل می‌شود.

مثال قانون پایستگی انرژی در ماشین آتوود

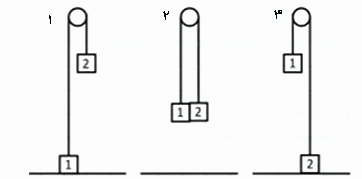
دو جعبه ۱ و ۲ به جرم‌های به ترتیب 15 و 18 کیلوگرم توسط نخ بدون جرمی به یکدیگر متصل شده‌اند. نخ از روی قرقره بدون جرم و اصطکاکی عبور کرده است. جعبه ۱ بر روی زمین و جعبه ۲ در ارتفاع ۳ متری از سطح زمین قرار دارد (تصویر ۱). دو جعبه از حالت سکون رها می‌شوند. سرعت جعبه‌ها را هنگامی که از کنار یکدیگر عبور می‌کنند به دست آورید (تصویر ۲). سرعت جعبه ۲ را هنگامی که به زمین می‌رسد به دست آورید (تصویر ۳).

پاسخ:

مبدا را سطح زمین و جهت عمودی به سمت بالا را مثبت در نظر می‌گیریم. انرژی مکانیکی سیستم برابر با جمع انرژی مکانیکی جعبه ۱ و ۲ است:

$$E = E_1+E_2 \\ E_1 = K_1 + U_1 \\ E_2 = K_2 + U_2$$

$$E= \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 +mgy_1 + mgy_2$$

$$y_1$$ و $$y_2$$ به ترتیب فاصله عمودی جعبه‌های ۱ و ۲ از سطح زمین هستند.

در تصویر ۱، جعبه ۱ بر روی زمین و جعبه ۲ در فاصله ۳ متری بالای زمین قرار دارد. بنابراین داریم:

$$y_1= 0 , y_2=3 m \\ y_1 + y_2 = 3 \\ y_2 = 3-y_1$$

در نتیجه انرژی مکانیکی کل به صورت زیر نوشته می‌شود:

$$E= \frac{1}{2} (m_1+m_2) v^2 \ +\ m_1gy_1 + m _2g (3-y_1)$$

ذکر این نکته مهم است که سرعت‌های دو جعبه با یکدیگر برابر هستند.

در حالت ۱ سیستم از حالت سکون رها می‌شود. بنابراین انرژی جنبشی کل سیستم برابر صفر است. همچنین جعبه ۱ بر روی زمین قرار دارد. در نتیجه، مقدار انرژی پتانسیل گرانشی آن نیز صفر خواهد بود.

$$E_1 = m_2gy_2 = 3m_2g = = 529.2 \ J$$

هنگامی که دو جعبه از کنار یکدیگر عبور می‌کنند (تصویر ۲) انرژی مکانیکی کل سیستم برابر است با:

$$E_2 = \frac{1}{2}(m_1+m_2)v^2 + 1.5 (m1+m_3)g\\ E_2 = 0.5(15+18)v^2 + (1.5 \ m) (15+18)9.8 =\\E_2 = 16.5v^2 + 4.85 \ J$$

ذکر این نکته مهم است که در حالت ۲، دو جسم در ارتفاع ۱.۵ متری از سطح زمین قرار دارند. یعنی جعبه ۱ به اندازه ۱.۵ متر به سمت پایین و جعبه ۲ به اندازه ۱.۵ متر به سمت بالا حرکت کرده‌اند. اکنون انرژی مکانیکی کل را در تصویر ۳ به دست می‌آوریم. در این حالت جسم ۱ در فاصله ۳ متری از سطح زمین و جسم ۲ بر روی زمین قرار گرفته است.

$$E_3 = 16.5v_3^2 + 3m_1g + 0 = 16.5 v_3^2 + 3\times 15\times 9.8=16.5 v_3^2 + 441$$

از آنجایی که در مثال فوق انرژی مکانیکی پایسته است داریم:

$$E_1=E_2=E_3$$

در نتیجه داریم:

$$E_1=E_2 \\ 529.2 = 16.5v_2^2 + 483.1 \\ v_2 = \sqrt{\frac{529.2-483.1}{16.5} }\\ v_2 = 1.63 \frac{m}{s} \\ E_2= E_3 \\ 529.2=16.5v_3^2 + 441 v_3=\frac{529.2-441}{16.5} \\ v_3 = \sqrt{\frac{529.2-441}{16.5} }\\ v_3=2.31 \frac{m}{s}$$

قانون بقای انرژی در سیالات

قانون پایستگی انرژی تحت عنوان قانون برنولی در سیالات نیز مورد استفاده قرار می‌گیرد. معادله برنولی یکی از مهم‌ترین معادلات مورد استفاده دز مکانیک سیالات است. در این معادله فشار و سرعت یک شاره روان به یکدیگر مربوط می‌شوند. این معادله در حالت کلی به صورت زیر نوشته می‌شود:

$$P_1+\frac{1}{2}\rho v_1^2+\rho g h_1 = P_2+\frac{1}{2}\rho v_2^2+\rho g h_2$$

بر طبق این معادله کاهش فشار در قسمتی از شاره با افزایش سرعت حرکت آن همراه خواهد بود. برای استخراج معادله بالا فرض شده است که نیروهای غیرپایستار بر سیستم وارد نمی‌شوند.

قانون بقای انرژی در ترمودینامیک چیست ؟

بر طبق قانون پایستگی انرژی یا اصل بقای انرژی در ترمودینامیک گرمای کل یا انرژی کل موجود در جهان ثابت است. رابطه میان گرما و کار منشا قانون اول پایستگی انرژی است. بر طبق این قانون، انرژی نه آفریده می‌شود، نه از بین می‌رود، بلکه از حالتی به حالت دیگر تبدیل می‌شود. به بیان دیگر، هنگامی که صورتی از انرژی ناپدید می‌شود، مقدار یکسان و برابری از صورت دیگر انرژی به وجود می‌آید. در این صورت، مقدار انرژی کل موجود در جهان ثابت خواهد ماند.

فرمول پایستگی انرژی در ترمودینامیک

فرض کنید مقدار q گرما به سیستمی متشکل از یک مول گاز در استوانه‌ای با پیستون متحرکِ بدون اصطکاکی منتقل شود.

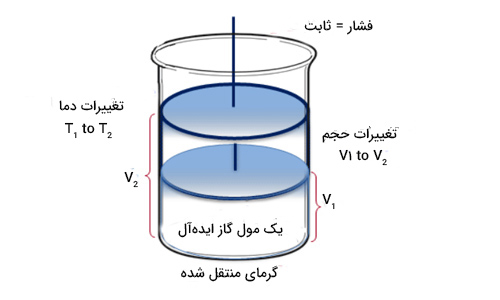
در فشار ثابت، حجم مولکول‌های گاز از $$V_1$$ به $$V_2$$ و دمای سیستم از $$T_1$$ به $$T_۲$$ تغییر می‌کند. بر طبق قانون اول ترمودینامیک q برابر است با:

$$q = dU + w$$

تغییرات انرژی داخلی = dU

اگر مقدار کار انجام شده به کار، حجم، فشار یا کار مکانیکی محدود شود آن‌گاه داریم:

$$w = PdV \\ q = dU + pdV$$

رابطه (۱)

اگر انرژی داخلی سیستم یعنی U تابعی از دما و حجم سیستم باشد داریم:

$$U=U(T,V)\\ dU=(\frac{\text{d}U}{\text{d}T})_V\ dT + (\frac{\text{d}U}{\text{d}V})_T \ dV$$

با قرار دادن رابطه بالا در رابطه (۱) داریم:

$$q=(\frac{\text{d}U}{\text{d}T})_V\ dT + (P+(\frac{\text{d}U}{\text{d}V})_T ) \ dV$$

در حجم ثابت V داریم:

$$(\frac{q}{dT})_V = (\frac{\text{d}U}{\text{d}T})_V = C_v$$

در نتیجه q به صورت زیر تغریف می‌شود:

$$q = C_vdT+(P+ (\frac{\text{d}U} {\text{d}V})_T) dV$$

برای گاز ایده‌آل داریم:

$$(\frac{\text{d}U}{\text{d}V})_T = 0$$

بنابراین q به صورت زیر نوشته خواهد شد:

$$q =nC_vdT + PdV$$

در مقابل برای گاز ایده‌آل داریم:

$$(\frac{\text{d}U}{\text{d}V})_T = \frac{an^2}{V^2} \\ q = nC_vdT + [P + \frac{an^2}{V^2}]dV$$

تغییرات گرما در ترمودینامیک برای گاز ایده‌آل یا گازهای واقعی از قانون اول ترمودینمیک و قانون گاز کامل یا معادله واندروالس به دست می‌آید. تمام گازهای ایده‌آل و واقعی از فرمول‌های بقای انرژی پیروی می‌کنند.

قانون اول ترمودینامیک برای برآیند چرخه‌ ای

تغییرات انرژی داخلی در فرآیند چرخه‌ای برابر صفر است، dU=0. بنابراین، بر طبق قانون اول ترمودینامیک (q=w)، گرما برای انجام فرآیند چرخه‌ای به طور کامل به کار تبدیل خواهد شد.

کار انجام شده در فرآیند هم‌ دما

تغییرات انرژی داخلی در فٰرآیند هم‌دما در گاز ایده‌آل به صورت زیر است:

$$dU=nC_vdT = 0$$

 در نتیجه q=w است. بنابراین، گرمای ترمودینامیکی به طور کامل به کار تبدیل می‌شود.

تغییرات انرژی در فرآیند هم‌ حجم

تغییرات حجم در فرآیند هم‌حجم برابر صفر است. در نتیجه، بر طبق اصل پایستگی انرژی داریم:

$$q=dU= nC_vdT$$

بنابراین تغییرات انرژی در فرآیند هم‌حجم، تنها انرژی داخلی سیستم یا دمای آن را تغییر می‌دهد.

قانون اول ترمودینامیک برای سیستم منزوی

در سیستم منزوی، نه ماده و نه انرژی از آن خارج یا به آن وارد می‌شوند. بنابراین مقدار q برابر صفر است. در نتیجه، طبق قانون پایستگی انرژی داریم:

w = -dU

از این‌رو، سیستم منزوی از انرژی داخلی برای انجام کار استفاده می‌کند.

قانون بقای انرژی انیشتین

یکی از مهم‌ترین نتایج تئوری نسبیت انیشتین هم‌ارزی انرژی و جرم و تبدیل آن‌ها به یکدیگر است. هم‌ارزی جرم و انرژی توسط فرمول معروف انیشتین بیان می‌شود. به عبارت دیگر، انرژی برابر حاصل‌ضرب جرم در مربع سرعت نور است:

$$E=mc^2$$

در آغاز قرن بیستم، در مورد تعریف جرم تجدیدنظر ریشه‌ای انجام شد. جرم، معنای مطلق بودن خود را از دست داد. یکی از جالب‌ترین نتایج نظریه نسبیت انیشتین، هم‌ارزی جرم و انرژی و تبدیل آن‌ها به یکدیگر است. از آنجایی که اندازه سرعت نور بسیار زیاد است، بر طبق رابطه معروف انیشتین، هر مقدار کوچکی از ماده مقدار بسیار زیادی انرژی دارد.

در نظریه نسبیت خاص، برخی از مواد ممکن است به وجود بیایند یا از بین بروند. اما، مقدار ماده و انرژی نسبت داده شده به چنین موادی در تمامی فرآیندها ثابت باقی خواهد ماند. ذکر این نکته مهم است که جرم حالت سکونِ هسته هر اتمی از مجموع جرم‌های سکون پروتون‌ها، نوترون‌ها و الکترون‌های تشکیل دهنده هسته کمتر است. این تفاوت جرم، به عنوان انرژی پیوندی هسته‌ای که انرژی لازم برای نگهداری هسته است در نظر گرفته می‌شود. بر طبق رابطه انیشتین،‌ انرژی پیوندی متناسب با تفاوت جرم است. به این تفاوت جرم، نقصان جرم گفته می‌شود.

در طی، تقسیم هسته‌ای یا شکافت هسته‌ای، جرم بعضی از هسته‌ها به مقدار بسیار زیادی انرژی تبدیل می‌شود.

تاکنون با مفهوم قانون پایستگی انرژی یا قانون بقای انرژی آشنا شدیم. آموختیم که مقدار انرژی کل در جهان ثابت است و انرژی نه به وجود می‌آید و نه از بین می‌رود، بلکه از صورتی به صورت دیگر تبدیل می‌شود. اما سوالی که ممکن است مطرح شود آن است که آیا تمام انرژی سیستم به انرژی مفید تبدیل می‌شود؟ پاسخ به این پرسش خیر است. در روند تبدیل انرژی در سیستمی دلخواه، همواره مقداری انرژی به صورت انرژی گرمایی هدر می‌رود. در نتیجه، در اینجا مفهومی به نام بازدهی انرژی تعریف می‌شود.

بازدهی انرژی چیست ؟

به مقدار انرژی سیستم که به انرژی مفید تبدیل می‌شود بازدهی انرژی می‌گوییم. بازدهی انرژی یکی از آسان‌ترین راه‌هایی است که در طی آن اتلاف انرژی حذف می‌شود و هزینه‌های انرژی کاهش می‌یابد.

مثال‌ های بازدهی انرژی در وسایل مختلف

هر جایی که انرژی استفاده می‌شود، شانس بهبود و افزایش بازده وجود دارد. برخی محصولات مانند لامپ‌های نورانی کم‌مصرف با مصرف مقدار کمتری انرژی، نور یکسانی را تولید می‌کنند.

• لامپ روشنایی: بازدهی لامپ‌های روشنایی LED در حدود 70 تا ۹۰ درصد است.
• پنجره‌ها: پنجره‌های کم‌مصرف از موادی ساخته شده‌اند که سبب کاهش تبادل گرما با محیط بیرون و نفوذ هوا به داخل می‌شوند. در نتیجه، برای گرم کردن محیط داخل خانه به انرژی زیادی نیاز نداریم.
• عایق: عایق‌بندی سقف و پنجره‌های خانه در زمستان از خروج گرما جلوگیری می‌کند. همچنین در تابستان، هوای گرم به داخل نفوذ نخواهد کرد. بنابراین، در زمستان برای گرم کردن خانه و در تابستان برای خنک کردن آن نیاز به مصرف بالای انرژی نیست.
• دماسنج‌های هوشمند: این دماسنج‌ها مجهز به ‌Wi-Fi هستند. با استفاده از آن‌ها می‌توان میزان گرما و سرما را در خانه‌ها کنترل کرد.
• خانه‌ها: به طور معمول میزان مصرف انرژی در هر خانواده بین دو تا پنج میلیون تومان در سال است. با استفاده از پنجره‌های کم‌مصرف و توجه به میزان مصرف انرژی، در هر ماه این هزینه تا حدود زیادی کاهش خوهد یافت.

حقایقی در مورد پایستگی انرژی

هنگامی که در خانه حوصله‌تان سر می‌رود در یخچال را به مدت طولانی باز نگه می‌دارید و به انتخاب خوراکی موردعلاقه‌تان فکر می‌کنید. اما آیا می‌دانید باز نگه داشتن در یخچال به مدت طولانی باعث افزایش مصرف انرژی در آن می‌شود؟ هر زمانی که در یخچال را باز می‌کنید در حدود سی درصد هوای سرد از آن خارج می‌شود. در نتیجه، انرژی بیشتری مصرف می‌شود و هزینه قبض برق نیز افزایش خواهد یافت.

اگر هنگام پخت غذا به جای فر برقی یا گازی از مایکرویو استفاده کنید، در مصرف انرژی به طور قابل‌ملاحظه‌ای صرفه‌جویی کرده‌اید. زیرا این وسیله در مقایسه با فر برقی یا گازی در حدود 50 درصد انرژی کمتری مصرف می‌کند.

در حدود ۷۵ درصد الکتریسیته مورد استفاده در خانه‌ها به هنگام خاموش بودن وسایل برقی مصرف می‌شود. به عنوان مثال، تلویزیون انرژی زیادی را هنگام خاموش بودن مصرف می‌کند. بنابراین، اگر به هنگام خاموش بودن وسایل برقی آن‌ها را از برق بکشیم، از هدر رفتن انرژی جلوگیری کرده‌ایم.

پاسخ به هر سوالی را در گوگل خواهید یافت. اما آیا می‌دانید گوگل باعث آلودگی جهان می‌شود. شاید عجیب به نظر برسد ولی هر بار سوالی در گوگل مطرح یا مطالب مرتبط با موضوعی جستجو می‌شود، در حدود ۰/۰۰۰۳ انرژی مصرف خواهد شد. همچنین، حدود ۰/۲ گرم دی‌اکسیدکربن وارد محیط زیست می‌شود.

تاکنون در مورد پایستگی انرژی صحبت کردیم و به پرسش پایستگی انرژی چیست با حل مثال‌های گوناگون پاسخ دادیم. اما در فیزیک، به جز انرژی، کمیت‌های مهم دیگری مانند تکانه نیز پایسته خواهند بود. در ادامه در مورد پایستگی تکانه توضیح می‌دهیم.

پایستگی تکانه

همان‌کونه که در مطالب بالا اشاره شد، در فیزیک عبارت پایسته در مورد کمیت‌های غیرقابل تغییر استفاده می‌شود. به عبارت دیگر، مقدار کمیت پایسته با گذشت زمان ثابت است و تغییری نمی‌کند. در واقع، مقدار کمیت پایسته قبل و بعد از یک اتفاق ثابت خواهد ماند. در فیزیک، سه کمیت بنیادی انرژی، تکانه و تکانه زاویه‌ای ثابت هستند. از پایستگی تکانه برای توصیف برخورد بین اجسام استفاده می‌شود.

مانند پایستگی انرژی، پایستگی تکانه نیز فقط برای سیستم منزوی به کار می‌رود. در این حالت نیروی خارجی بر سیستم منزوی وارد نمی‌شود. این عبارت به چه معنا است؟ به عنوان مثال، به هنگام برخورد دو جسم با یکدیگر، دو جسم و هر چیزی را که بر آن‌ها نیرو برای مدت زمان معینی وارد می‌کند جزو سیستم منزوی در نطر می‌گیریم.

اگر i و f نشان‌دهنده نکانه‌های اولیه و نهایی اجسام داخل سیستم باشند، اصل پایستگی تکانه به صورت زیر نوشته خواهد شد:

$$P_{1i}+P_{2i} + ... = P_{1f}+P_{2f} + ...$$

چرا تکانه پایسته است ؟

پایستگی تکانه نتیجه مستقیم قانون سوم نیوتن است.

برخورد دو جسم A و B را در نظر بگیرید. هنگامی که این دو جسم با یکدیگر برخورد می‌کنند، بر جسم A از طرف جسم B نیروی $$F_{AB}$$ وارد خواهد شد. طبق قانون سوم نیوتن، نیرویی مساوی و در خلاف جهت این نیرو از طرف جسم A بر جسم B وارد می‌شود ($$F_{BA}$$).

$$F_{AB} = - F_{BA}$$

این نیروها، بین اجسام به هنگام برهم‌کنش وارد خواهند شد. مدت زمانی که دو جسم با یکدیگر در تماس هستند با $$t_{AB}$$ یا $$t_{BA}$$ نشان داده می‌شود.

$$t_{AB} = t_{BA}$$

حاصل‌ضرب نیروی وارد شده بر هر جسم و مدت زمان اعمال آن نیرو برای هر جسم برابر است با:

$$F_{AB}\times t_{AB} = - t_{BA}\times t_{BA}$$

حاصل‌ضرب نیرو در زمان برابر تغییرات تکانه است. در نتیجه، تغییرات تکانه اجسام با یکدیگر برابر، اما در خلاف جهت یکدیگر هستند. به عبارت دیگر، جمع تغییرات تکانه برابر صفر خواهد بود.

$$m_A \triangle v_A= - m_B \triangle v_B \\ m_A \triangle v_A + m_B \triangle v_B = 0$$

نکات جالب در مورد پایستگی تکانه

چهار نکته جالب در مورد پایستگی تکانه وجود دارد:

1. تکانه کمیت برداری است. در نتیجه، به هنگام جمع تکانه‌های اجسام مختلف در یک سیستم منزوی، باید از جمع برداری استفاده کنیم. سیستمی متشکل از دو جسم مشابه را در نظر بگیرید. این اجسام با سرعت یکسان از یکدیگر دور می‌شوند. نکته جالب در مورد این سیستم آن است که با وجود آن‌که اجسام در حال حرکت هستند تکانه کل سیستم برابر صفر است.
2. تحلیل برخورد اجسام با یکدیگر با استفاده از قانون پایستگی تکانه بسیار جالب است. دلیل این امر آن است که برخوردها بسیار سریع اتفاق می‌افتند، بنابراین زمان برخورد اجسام با یکدیگر بسیار کوتاه خواهد بود. زمان برهم‌کنش بسیار کوتاه به معنای کوچک بودن $$F \times \triangle t$$ است.
3. به طور معمول، اندازه‌گیری و دنبال کردن تکانه، حتی در سیستم‌های بسیار پیچیده، راحت است. برخورد دو توپ هاکی روی یخ را در نظر بگیرید. برخورد به اندازه‌ای قدرتمند است که یکی از توپ‌ها به دو قطعه شکسته خواهد شد. انرژی جنبشی هنگام برخورد پایسته نیست، اما تکانه پایسته خواهد ماند. با دانستن سرعت‌ها و جرم‌های اجسام بلافاصله بعد از برخورد، می‌توانیم از پایستگی تکانه استفاده کنیم. نکته جالب آن است که در این حالت از قانون پایستگی انرژی نمی‌توانیم استفاده کنیم.
4. برخورد با اجسام ساکن جالب است. البته ذکر این نکته مهم است که هیچ جسمی به طور کامل ساکن نیست، اما جرم برخی اجسام به قدری زیاد است که ساکن به نظر می‌رسند. توپی به جرم m را در نظر بگیرید که با سرعت v به دیوار آجری برخورد می‌کند. این توپ پس از برخورد با دیوار با سرعت v- به سمت عقب برمی‌گردد. دیوار محکم به زمین وصل شده و ساکن است. اما تکانه توپ به اندازه 2mv تغییر کرده است.

به هنگام برخورد توپ به دیوار تکانه پایسته خواهد بود. در نتیجه، تکانه زمین و دیوار نیز باید به اندازه 2mv تغییر کند. اما به دلیل آن‌که زمین از توپ بسیار سنگین‌تر است متوجه تغییر تکانه آن نخواهیم شد.

مثال اول پایستگی تکانه

به احتمال قوی در زمان کودکی کارتون‌های زیادی در مورد حمله دزدان دریایی به کشتی مسافران دیده‌اید. بیشتر دزدان دریایی برای حمله از شلیک توپ استفاده می‌کنند. فرض کنید توپ ۲ کیلوگرمی از توپ‌افکنی به جرم ۵۰۰ کیلوگرم به صورت افقی شلیک شود. اگر توپ با سرعت 200 متر بر ثانیه شلیک شود، توپ‌افکن با چه سرعتی به عقب رانده خواهد شد؟

پاسخ 

توپ‌افکن (Cannon) و توپ (Ball) قبل از شلیک در حالت سکون قرار دارند. از آنجایی که تکانه پایسته است، در همه زمان‌ها رابطه زیر برقرار است:

$$\overrightarrow{p}_c + \overrightarrow{p}_b = 0$$

در این مثال، تمامی حرکت‌ها در جهت افقی رخ می‌دهد. در نتیجه، برای سرعت از کمیت نرده‌ای استفاده می‌کنیم.

$$m_cv_c \ + m_b v_b = 0 \\ \frac{m_bv_b}{m_c}= -v_c \\ \frac{2 kg \times 200 \ m/s}{500 \ kg} = -0.8 \ m/s$$

مثال دوم پایستگی تکانه

فرض کنید توپ‌افکن با زاویه 30 درجه نسبت به افق توپ را شلیک می‌کند. در این حالت سرعت به عقب راندن توپ‌افکن را به دست آورید. تکانه اضافه کجا می‌رود؟

پاسخ

از آنجایی که توپ‌افکن تنها در امتداد کشتی و به صورت افقی حرکت می‌کند، تنها مولفه افقی تکانه برای ما جالب خواهد بود.

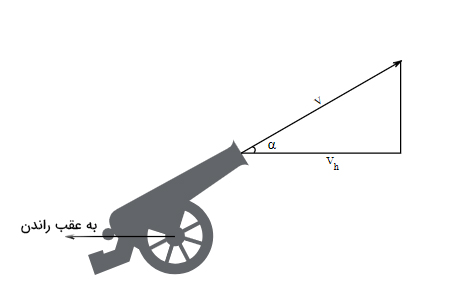
برای مولفه افقی سرعت داریم:

$$v_h = v_b cos \alpha \\ = 173 \frac{m}{s}$$

در نتیجه سرعت عقب راندن توپ‌افکن به صورت زیر به دست خواهد آمد:

$$\frac{m_bv_h}{m_c} = -v_c \\ \frac{2 \ kg\times 173 \ m/s}{500 \ kg} = - 0.69 \ m/s$$

مولفه عمودی تکانه، کشتی را به درون آب هل می‌دهد.

مثال سوم پایستگی تکانه

سیبی به جرم ۰/۷ کیلوگرم بر روی میزی در حالت سکون قرار دارد. در این هنگام پرتقالی به وزن 0/4 کیلوگرم و با سرعت 5 متر بر ثانیه به آن برخورد می‌کند. اگر سرعت سیب بلافاصله پس از برخورد 3 متر بر ثانیه باشد، سرعت پرتقال را به دست آورید.

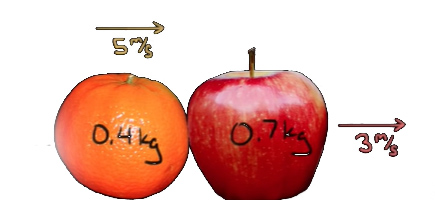
پاسخ

سرعت پرتقال بلافاصله بعد از برخورد را با $$v_O$$ نشان می‌دهیم. اما سوالی که ممکن است مطرح شود آن است که پرتقال پس از برخورد با سیب به کدام سمت حرکت خواهد کرد؟ به سمت راست یا چپ؟

برای حل این مثال، پرتقال و سیب را به عنوان سیستم واحد در نظر می‌گیریم. از آنجایی که نیروی خارجی بر سیستم وارد نمی‌شود، تکانه قبل از برخورد با تکانه بعد از برخورد برابر خواهد بود.

$$\overrightarrow{P}_i=\overrightarrow{P}_f$$

در نتیجه داریم:

$$(0.4 \ kg) \times (5 \ \frac{m}{s})+ (0.7 \ kg) \times ( 0 \frac{m}{s}) = (0.4 \ kg) \times (v_O \ \frac{m}{s})+ (0.7 \ kg) \times ( 3 \frac{m}{s}) \\ 2 \ kg \frac{m}{s} = (0.4 \ kg) v_O + 2.1 \ kg \frac{m}{s} \\ v_O = -0.25 \ \frac{m}{s}$$

سرعت پرتقال بلافاصله بعد از برخورد 0/25- متر بر ثانیه به دست می‌آید. علامت منفی نشان‌دهنده آن است که پرتقال پس از برخورد با سیب به سمت چپ حرکت کرده است.

مسائل برخورد در دو بعد را چگونه حل کنیم؟

به هنگام برخورد دو جسم با یکدیگر در دوبعد، تکانه در هر راستا به طور مستقل پاسته خواهد بود. به بیان دیگر، تکانه کل در راستای x، قبل و بعد از برخورد یکسان است.

$$\sum P_{xi} = \sum P_{xf}$$

همچنین، تکانه کل در راستای y قبل و بعد از برخورد یکسان خواهد بود.

$$\sum P_{yi} = \sum P_{yf}$$

برای حل مسائل برخورد در دو بعد، گام‌های زیر را به ترتیب طی می‌کنیم:

1. تعیین تمام اجسام داخل سیستم: اجسام را از یکدیگر جدا کنید و در صورت لزوم قبل و بعد از برخورد آن‌ها را رسم کنید.
2. تمامی مقادیر داده شده در پرسش را بنویسید و مقادیری را که نیاز به محاسبه دارند به طور دقیق مشخص نمایید.
3. انتخاب دستگاه مختصات: اگر تعداد زیادی سرعت و نیرو در جهت مشخصی قرار گرفتند، عاقلانه‌ترین کار استفاده از دستگاه مختصات مناسب است.
4. تعیین نیروهای وارد شده بر هر جسم در سیستم: به یاد داشته باشید که پایستگی تکانه تنها در حالتی برقرار است که هیچ نیروی خارجی بر سیستم انتخابی وارد نشود.
5. نوشتن معادلات یا رابطه‌های تساوی تکانه سیستم قبل و بعد از برخورد: معادلات پایستگی تکانه در راستای x و y را به صورت جداگانه بنویسید.
6. حل معادلات به منظور تعیین مقادیر خواسته شده.
7. جایگزینی مقدارهای داده شده در معادلات برای یافتن مقادیر نامشخص:‌ اکر نیاز به جمع برداری بود، بهتر است آن را به صورت گرافیکی و با کشیدن بردارها به صورت دستی انجام دهیم.

مثال پایستگی تکانه در دو بعد

توپ A به جرم ۱۰ کیلوگرم با سرعت 3 متر بر ثانیه به سمت راست حرکت می‌کند. این توپ به توپ ‌‌B به جرم 5 کیلوگرم برخورد می‌کند. توپ A پس از برخورد با توپ B با سرعت ۲ متر بر ثانیه و با زاویه ۳۰ درجه نسبت به افق به حرکت خود ادامه می‌دهد. سرعت توپ ‌B را به دست آورید.

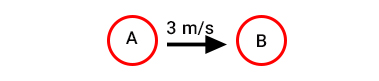
پاسخ

تاکنون پایستگی انرژی در یک‌بعد بررسی شد. برای حل این مثال باید پایستگی تکانه را در دوبعد در نظر بگیریم.

$$p_{ix} = (10 \ kg) \times (3 \frac{m}{s}) = 30\\ p_{iy} = 0$$

بر طبق قانون پایستگی تکانه، تکانه باید در راستای x و y به طور جداگانه پایسته باشد. این جمله بدان معنا است که مقدار نهایی تکانه در راستای ‌x باید برابر 30 و مقدار آن در راستای y باید برابر صفر باشد.

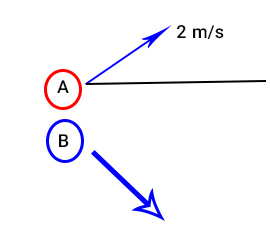
مولفه‌های x و y سرعت توپ‌ A را پس از برخورد به دست می‌آوریم.

$$_{Ax} = 2\ cos 30^o = \sqrt{3} \frac{m}{s}\\ v_{Ax} = 2\ sin 30^o = 1 \frac{m}{s}$$

در نتیجه تکانه‌های نهایی توپ A به صورت زیر نوشته می‌شوند:

$$P_{Ax} = 10\sqrt{3} \ \frac{m}{s}\\ P_{Ay} = 10 \ \frac{m}{s}$$

برای پایستگی تکانه در راستای y داریم:

$$P_{Ay} + P_{By} = 0 \\ 10 + P_{By} = 0 \\ P_{By} = -10 \ kg m/s$$

مقدار مولفه y تکانه توپ B برابر 10- است. اکنون سرعت این توپ را در راستای y به دست می‌آوریم:

$$m_Bv_{By} = P_{By} \\ 5 \times v_{By} = -10 \\ v_{By} = -2\ \frac{m}{s}$$

اکنون سرعت توپ B را در راستای x به دست می‌آوریم:

$$P_{Ax} + P_{Bx} = 30 \\ 10 \sqrt{3} + P_{Bx} = 30 \\ P_{Bx} =12.7 \\ P_{Bx} = m_B v_{Bx} \Rightarrow 12.7 = 5 \times v_{Bx} \Rightarrow v_{Bx} = 2.2 \ \frac{m}{s}$$

معرفی فیلم آموزش فیزیک پایه ۱

مجموعه فرادرس در تولید و محتوای آموزشی خود اقدام به تهیه فیلم آموزش فیزیک پایه 1 برای دانش‌آموزان پایه دوازدهم و دانشجویان ترم اول علوم پایه و فنی مهندسی کرده است. این مجموعه آموزشی از سیزده درس تشکیل شده است که برای آشنایی بیشتر با مباحث پایستگی انرژی و تکانه، درس‌های ششم تا هشتم مفید هستند. ذکر این نکته مهم است که برای حل مسائل مربوط به پایستگی تکانه در دوبعد آشنایی با قوانین جمع و تجزیه بردارها نیز مهم خواهد بود.

درس دوم در مورد قوانین بردارها، مفهوم بردار و کمیت نرده‌ای، جمع و ضرب بردارها و برخی از بردارها در فیزیک است. پس از تماشای این درس با مفهوم بردارها و قوانین حاکم بر جمع و ضرب آن‌ها به خوبی آشنا خواهید شد و مسائل مربوط به برخورد در دو بعد را به راحتی حل می‌کنید.

در این مطلب به پرسش قانون پایستگی انرژی چیست پاسخ دادیم. در درس هفتم این مجموعه آموزشی با نیروهای پایستار، انرژی پتانسیل، سیستم‌های پایستار و مفهوم قانون پایستگی انرژی چیست همراه با حل مثال‌های گوناگون آشنا می‌شوید.

در درس هشتم این مجموعه آموزشی تکانه و برخورد و پایستگی تکانه در حین برخورد آموزش داده می‌شود.

• برای دیدن فیلم آموزش فیزیک پایه 1 + اینجا را کلیک کنید. 

جمع‌بندی

در این مطلب به پرسش پایستگی انرژی چیست پاسخ دادیم. فهمیدیم مقدار انرژی کل در جهان ثابت است و انرژی نه از بین می‌رود، نه به وجود می‌آید، بلکه تنها از حالتی به حالت دیگر تبدیل می‌شود. همچنین، با قانون بقای انرژی مکانیکی همراه با حل مثال‌های گوناگون آشنا شدیم. قانون بقای انرژی را در ماشین آتوود بررسی کردیم و آموختیم قانون پایستگی انرژی در شاره‌ها یا سیالات تحت عنوان اصل برنولی برقرار است. در پایان، پایستگی تکانه در یک و دوبعد بررسی شد. ذکر این نکته مهم است که برای برقرار پایستگی انرژی و تکانه سیستم مورد مطالعه باید منزوی باشد و از طرف محیط بیرون بر آن نیرویی وارد نشود.