نیروی جاذبه چیست؟ — به زبان ساده

بیشتر ما داستان معروف نیوتن و افتادن سیب بر روی سر او را شنیدهایم. سیبی که سبب کشف یکی از مهمترین قانونهای طبیعت به نام قانون جهانی گرانش یا نیروی جاذبه شد. ذکر این نکته مهم است که نیروی گرانش نیرویی از نوع جاذبه و نه دافعه است و در زبان عامیانه به نیروی گرانش، نیروی جاذبه (جاذبه زمین) گفته میشود. نیروی جاذبه یکی از بنیادیترین نیروهای جهان است که در هر لحظه از زندگی روزمره، آن را تجربه میکنیم. این نیرو، ما و هر جسمی در اطرافمان را بر روی زمین نگه میدارد. در این مطلب در مورد نیروی گرانش یا جاذبه صحبت و ویژگیهای مهم این نیرو را به زبان ساده توضیح خواهیم داد.
نیروی جاذبه چیست ؟
نیروی جاذبه همانطور که از نامش مشخص است سبب کشش اجسام به سمت یکدیگر میشود. جاذبه، نیرویی است که به واسطه آن سیاره یا هر جسم دیگری، اجسام مختلف را به سمت مرکز خود میکشاند. این نیرو، تمام سیارهها را در مدارهای مختلف به دور خورشید نگه داشته است. این نیرو بین همه اجسام وجود دارد و یکی از ضعیفترین نیروهای شناخته شده در طبیعت است. اما سوالی که ممکن است مطرح شود آن است که نیوتن چگونه با افتادن سیب به وجود نیروی جاذبه پی برد؟ خالی از لطف نیست که این داستان را با نگاه علمیتری بازگو کنیم.

داستان سیب و نیروی جاذبه
داستان افتادن سیب روی سر نیوتن را میتوانیم به چند مرحله تقسیم کنیم:
- سیب شتاب میگیرد.
- سرعت اولیه سیب صفر است. سرعت آن پس از افتادن از درخت از صفر تا مقدار معینی افزایش مییابد.
- بر طبق قانون دوم نیوتن، نیرویی باید بر سیب وارد و سبب شتاب گرفتن آن شده باشد. به این نیرو، نیروی جاذبه و به شتاب سیب، شتاب ناشی از جاذبه میگوییم.
- فرض کنید ارتفاع درخت دو برابر بود. انتظار داریم که سیب پس از کنده شدن از درخت به سمت زمین شتاب بگیرد، بنابراین نیروی جاذبه بر سیبی روی بلندترین درختهای سیب نیز وارد خواهد شد.
قانون جهانی گرانش نیوتن
نیوتن، شتاب ماه را با شتاب اجسام بر روی زمین مقایسه کرد. او اعتقاد داشت که نیروهای جاذبه مسئول شتاب بر روی زمین یا ماه هستند. او به نتیجه مهمی در مورد رابطه بین جاذبه و فاصله پی برد. بر طبق یافتههای او، نیروی جاذبه بین زمین و دیگر اجسام با فاصله زمین و مرکز جسم، رابطه معکوس دارد. اما باید به این نکته توجه داشته باشیم که بزرگی نیروی جاذبه به عاملهای دیگری به جز فاصله، بستگی دارد. به معادله معروف نیوتن توجه کنید:
نیوتن میدانست که نیرویی که سبب شتاب دادن به سیب و افتادن آن شد، باید به جرم سیب وابسته باشد. همچنین، بر طبق قانون سوم نیوتن، این نیرو باید شتابی برابر و رو به بالایی بر زمین وارد کند. بنابراین، این نیرو به جرم زمین نیز وابسته است. در نتیجه، بر طبق یافتههای نیوتن، نیروی جاذبه باید:
- به طور مستقیم متناسب با جرم زمین باشد.
- به طور مستقیم متناسب با جرم جسم باشد.
- متناسب با عکس مجذور فاصله مرکزهای زمین و جسم باشد.
معادله جهانی گرانش
قانون جهانی گرانش فراتر از زمین و اجسام روی آن است. این قانون در مورد جهانی بودن نیروی جاذبه یا گرانش است. جایگاه نیوتن در قانون جاذبه به دلیل کشف این قانون نیست، بلکه به خاطر کشف جهانی بودن این نیرو است. تمام اجسام، یکدیگر را با نیروی جاذبه به سمت یکدیگر میکشند. این نیرو به طور مستقیم با جرم دو جسم متناسب و با مجذور فاصله بین مرکزهای آنها، به طور معکوس متناسب است. رابطه ریاضی نیروی جاذبه به صورت زیر نوشته میشود:
در رابطه فوق:
- : نیروی جاذبه بین دو جسم
- : جرم جسم اول
- : جرم جسم دوم
- : فاصله بین مرکزهای دو جسم
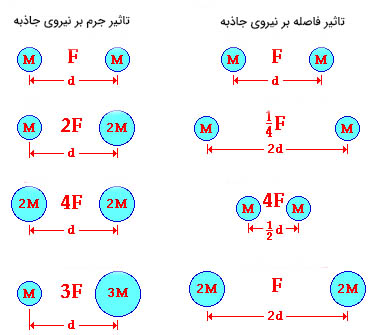
از آنجایی که جاذبه، مستقیم با جرم دو جسمِ برهمکنشکننده، متناسب است، هر چه جرم آنها بیشتر باشد، با نیروی جاذبه بزرگتری به سمت یکدیگر جذب خواهند شد. بنابراین، با افزایش جرم هر یک از دو جسم (در فاصلهای ثابت)، جاذبه بین آنها نیز به تناسب افزایش خواهد یافت. اگر جرم یکی از اجسام دو برابر شود، نیروی بین آنها نیز دو برابر میشود. اگر جرم یکی از دو جسم سه برابر شود، نیروی جاذبه بین آنها نیز سه برابر خواهد شد. اگر جرم هر یک از دو جسم به طور جداگانه ۲ برابر شوند، جاذبه بین آنها ۴ برابر میشود.
به رابطه نوشته شده برای نیروی جاذبه دقت کنید. این نیرو، به طور معکوس با مجذور فاصله بین دو جسم، متناسب است. بنابراین، هر چه فاصله بین دو جسم بیشتر باشد، جاذبه بین آنها کمتر است، و هر چه فاصله بین آنها کمتر باشد، جاذبه بین آنها بیشتر خواهد بود. به عنوان مثال، اگر فاصله دو جسم دو برابر شود، نیروی جاذبه بین آنها یکچهارم میشود. اگر فاصله بین دو جسم نصف شود، نیروی بین آنها چهار برابر خواهد شد.
تناسب نیروی جاذبه با جرم دو جسم و فاصله بین آنها، در تصویر زیر نشان داده شده است. با دقت به تصویر زیر، متوجه خواهید شد که جاذبه چگونه با فاصله و جرم دو جسم تغییر میکند.
ثابت جهانی گرانش
در رابطه نوشته شده برای نیروی جاذبه، از تساوی استفاده نکردیم. برای استفاده از تساوی در این رابطه، باید از ثابت تناسب استفاده کنیم. بنابراین، معادله بالا به صورت زیر نوشته میشود:
ثابت تناسب G در معادله بالا به عنوان ثابت جهانی گرانش شناخته شده است. مقدار دقیق این ثابت در حدود یک قرن پس از فوت نیوتن، توسط «هنری کاوندیش» (Henry Cavendish) به طور تجربی محاسبه شد.
یکای نوشته شده برای G کمی عجیب به نظر میرسد. اما اگر این واحد در معادله فوق نوشته شود، واحد اندازهگیری نیرو برابر نیوتن بهدست خواهد آمد.
در مطالب فوق گفتیم که نیوتن رابطه بین حرکت ماه و حرکت سقوط آزاد جسمی بر روی زمین را کشف کرد. او با استفاده از نظریههای جاذبه و دینامیکی، قانونهای کپلر را توضیح داد و علم مدرن گرانش را پایهگذاری کرد. بر طبق فرضیههای نیوتن، نیروی جاذبه بین هر دو جسم جرمداری وجود دارد و از نوع نیروهای غیرتماسی است. بر طبق قانون اول نیوتن یا اینرسی (اگر بر جسمی نیروی خارجی وارد نشود، جسم در حالت سکون باقی خواهد ماند یا به حرکت خود با سرعت ثابت بر خط راست ادامه میدهد)، نیروی وارد شده بر ماه از طرف زمین برای حفظ حرکت دایرهای آن به دور زمین لازم است. نیوتن فهمید که نیروی بین زمین و ماه، از نوع نیروهای بلندبرد و مشابه نیرویی است که زمین بر اجسام مختلف در نزدیکی سطح خود وارد میکند.
بر طبق یافتههای نیوتن، جاذبه ماه کوچکتر از جاذبه بر روی سطح زمین است. او عدد ۳۶۰۰ را به مربع شعاع زمین ربط داد. بر طبق محاسبات انجام شده توسط نیوتن، حرکت دایرهای به شعاع R و با دوره تناوب T، شتاب ثابتی برابر A دارد که با استفاده از رابطه زیر بهدست میآید:
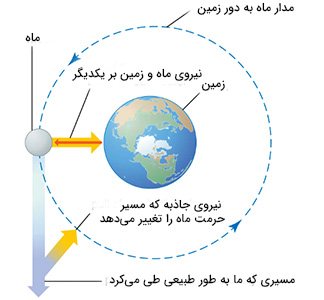
شعاع مدار ماه در حدود ۳۸۴ هزار کیلومتر و دوره تناوب آن ۲۷/۳ روز است. نیوتن شتاب ماه در مدار خود را ۰/۰۰۲۷ متر بر مجذور ثانیه بهدست آورد. این عدد برابر شتاب سقوط جسمی بر روی سطح زمین است.
بر طبق نظریه نیوتن، هر ذره کوچکی، ذرات دیگر را از طریق نیروی جاذبه جذب میکند. جاذبه هر جسم محدودی با تقارن کروی به گونهای است که گویا تمام جرم جسم در مرکز آن جمع شده است.
نیروی جاذبه تعدادی جسم با جرمهای یکسان و بر جسمی به جرم M برابر است با:
علامت جمع بر روی جرمهای بدان معنا است که نیروهای جاذبه وارد بر جرم M باید به صورت برداری با یکدیگر جمع شوند.
محاسبه ثابت جهانی گرانش
گفتیم ثابت جهانی گرانش توسط کاوندیش اندازه گرفته شد. همچنین فهمیدیم که نیروی جاذبه متناسب با جرم دو جسم است و با مجذور فاصله بین آنها به طور معکوس تغییر میکند. فرمول نیروی جاذبه به صورت زیر نوشته می شود:
ثابت جهانی گرانش در سال ۱۷۹۸ توسط کاوندیش با استفاده از ترازوی پیچشی اندازه گرفته شد.
ابزار کاوندیش از قسمتهای زیر تشکیل شده بود:
- میلهای محکم و سبک به طول ۰/۶ متر
- دو کره سربی کوچک که به دو انتهای میله متصل شده بودند.
- سیم نازکی متصل به یک نقطه که به میل وصل شده بود.
هنگامی که میله میپیچد، پیچش میله نیرویی پیچشی متناسب با زاویه چرخش آن، اعمال خواهد کرد. هر چه مقدار پیچش یا زاویه چرخش بزرگتر باشد، سیستم با نیروی بیشتری تمایل به بازگشت به حالت اولیه خود دارد. کاوندیش به منظور تعیین رابطه میان زاویه چرخش و اندازه نیروی پیچشی، وسیله خود را کالیبره کرد.
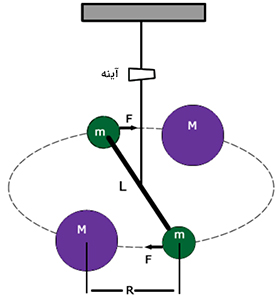
این دانشمند برای تکمیل این ابزار، دو کره سربی بزرگ را نزدیک دو کره کوچکتر قرار داد. از آنجایی که تمام جرمها، یکدیگر را جذب میکنند، کرههای بزرگتر نیروی جاذبهای بر کرههای کوچکتر وارد میکنند و میله را به اندازه مشخصی میچرخانند. هنگامی که نیروی پیچشی و نیروی جاذبه با یکدیگر برابر شوند، میله و کرهها در حالت سکون قرار میگیرند. کاوندیش توانست نیروی جاذبه بین جرمها را اندازه بگیرد. با دانستن جرم کرههای کوچکتر و مقدار نیروی جاذبه، مقدار ثابت جهانی گرانش محاسبه شد.
مقدار G بسیار کوچک است. این مقدار کوچک نشان میدهد که نیروی جاذبه تنها برای اجسامی با جرمهای بسیار بزرگ، قابل ملاحظه است.
جرم و وزن
در مطالب بالا معادله کلی نیروی جاذبه بین دو جسم با جرمهای مختلف را نوشتیم. اکنون میخواهیم مقدار این نیرو را روی سطح زمین بهدست آوریم. رابطه کلی نیروی جاذبه را به صورت کلی داریم:
اگر جسمی به جرم m در ارتفاع h از سطح زمین قرار داشته باشد، برای بهدست آوردن مقدار نیروی جاذبهای که زمین بر جسم وارد میکند، به جای جرم جسم، به جای جرم زمین یعنی و به جای فاصله بین دو جسم (d) ( شعاع زمین است) را قرار میدهیم. در نتیجه، رابطه بالا، به صورت زیر نوشته میشود:
به این نکته توجه داشته باشید که h در مقابل بسیار کوچک است، بنابراین میتوان از آن در مقابل شعاع زمین صرفنظر کرد. در نتیجه، نیروی وزن بر روی سطح زمین یا نزدیک آن به صورت زیر نوشته میشود:
شتاب جاذبه بر روی سطح زمین به صورت زیر تعریف میشود:
با قرار دادن مقدارهای ثابت جهانی گرانش، جرم و شعاع زمین در رابطه بالا، مقدار g برابر ۹/۸ متر بر مجذور ثانیه بهدست میآید. در نتیجه، مقدار نیروی جاذبهای که از طرف زمین بر جسمی وارد میشود برابر F = mg است و به آن نیروی وزن میگوییم. به بیانی دیگر، وزن نیرویی است که در اثر کشش گرانش بر روی جسمی ایجاد و بر حسب نیوتن اندازه گرفته میشود. اما جرم مقدار ماده در جسم و واحد اندازهگیری آن کیلوگرم است.
نیروی جاذبه بر جسمی به جرم یک کیلوگرم بر روی سطح زمین برابر ۱۰ نیوتن است که برابر g است.

جرم و وزن در جدول زیر با یکدیگر مقایسه شدهاند.
| جرم | وزن |
| جرم ویژگی ماده و مقدار آن در هر جایی یکسان است. | مقدار وزن به جاذبه بستگی دارد و مقدار آن با افزایش یا کاهش جاذبه زیاد یا کم میشود. |
| مقدار جرم هیچگاه صفر نیست. | اگر هیچ جاذبهای بر جسم اعمال نشود، مقدار وزن آن صفر خواهد بود (فضا) |
| جرم با تغییر مکان، تغییر نمیکند. | وزن با تغییر مکان، تغییر خواهد کرد. |
| جرم کمیتی نردهای است و تنها مقدار دارد. | وزن کمیتی برداری و دارای بزرگی و جهتی به سمت مرکز زمین یا هر مرکز جاذبهای است. |
| جرم میتواند با استفاده از ترازویی معمولی اندازه گرفته شود. | وزن با استفاده از ترازوی فنری اندازه گرفته میشود. |
| واحد اندازهگیری جرم به طور معمول گرم و کیلوگرم است. | واحد اندازهگیری وزن، نیوتن، است. |
وزن در سیاره های مختلف
در تفاوت جرم و وزن گفتیم که مقدار جرم در هر نقطهای در جهان یکسان است، اما وزن از نقطهای به نقطه دیگر تغییر خواهد کرد. دلیل این امر آن است که وزن جسم بر روی سیارهای خاص به شتاب جاذبه آن سیاره بستگی دارد. مقدار شتاب جاذبه به جرمِ سیاره و فاصله مرکز آن تا جسم بستگی دارد. به عنوان مثال، وزن ما بر روی کوه اندکی کمتر از سطح دریا است. شتاب جاذبه اعمال شده بر جسمی در سیاره مشتری در حدود ۳۱۶ برابر بزرگتر از مقدار این کمیت بر روی سطح زمین است، اما وزن فرد ۳۱۶ برابر نخواهد بود. دلیل این امر آن است که فاصله مرکز مشتری تا سطح آن بسیار بزرگ است. وزن فرد در سیاره مشتری ۲/۶۴ برابر وزن او بر روی سطح زمین خواهد بود.
مقدار شتابهای جاذبه خورشید و سیارههای مختلف در جدول زیر با یکدیگر مقایسه شدهاند.
| نام سیاره یا ستاره | جاذبه سطحی بر حسب | چند برابر جاذبه زمین |
| خورشید | ۲۷/۹۰ | ۲۷۴/۱ |
| عطارد یا تیر | ۰/۳۷۷۰ | ۳/۷۰۳ |
| زهره | ۰/۹۰۳۲ | ۸/۸۷۲ |
| زمین | یک (مرجع) | ۹/۸۲۲۶ |
| ماه | ۰/۱۶۵ | ۱/۶۲۵ |
| مریخ | ۰/۳۸۹۵ | ۳/۷۲۸ |
| مشتری | ۲/۶۴۰ | ۲۵/۹۳ |
| زحل | ۱/۱۳۹ | ۱۱/۱۹ |
| اورانوس | ۰/۹۱۷ | ۹/۰۱ |
| نپتون | ۱/۱۴۸ | ۱۱/۲۸ |
نمونه سوالات نیروی جاذبه
تاکنون با نیروی جاذبه، تعریف آن و شتاب جاذبه آشنا شدیم. در ادامه نمونه سوالاتی در مورد این نیرو حل خواهیم کرد
محاسبه شتاب جاذبه بر روی سطح ماه
مقدار شتاب جاذبه بر روی سطح ماه را بهدست آورید. جرم ماه برابر و شعاع آن برابر متر است.
پاسخ:
اگر جسمی در نزدیکی سطح ماه قرار داشته باشد، از طرف ماه، نیروی جاذبهای بر آن وارد خواهد شد که جهت این نیرو به سمت مرکز ماه است. تنها، نیروی جاذبه بر جسم وارد میشود، بنابراین، بر طبق قانون دوم نیوتن، این نیرو شتابی به نام شتاب جاذبه به جسم خواهد داد. بر طبق قانون سوم نیوتن، جسم نیز نیرویی برابر نیروی جاذبه و در خلاف جهت بر ماه وارد میکند و آن را به سمت خود میکشاند.
با حذف m از طرفین رابطه بالا، داریم:
دیدیم را با g نشان میدهیم. مقدار G برابر است. با قرار دادن مقدارهای داده شده در رابطه g، مقدار آن را محاسبه میکنیم:
مقایسه شتاب جاذبه زمین بر روی سطح و در ارتفاع مشخصی بالای آن
مقدار شتاب جاذبه را برای هر یک از حالتهای زیر بهدست آورید.
- بر روی سطح زمین
- و در ارتفاع ۳۵۰۰ کیلومتری از سطح آن بهدست آورید.
جرم و شعاع زمین به ترتیب برابر کیلوگرم و متر هستند.
پاسخ: در ابتدا، شتاب جاذبه را بر روی سطح زمین بهدست میآوریم:
اکنون، جسم از سطح زمین دور میشود. از آنجایی که شتاب جاذبه با مجذور فاصله به صورت معکوس تغییر میکند، با دور شدن جسم از سطح زمین، مقدار شتاب جاذبه کاهش خواهد یافت. در این حالت، مقدارهای G و M ثابت هستند، اما مقدار R افزایش یافته و برابر جمع شعاع زمین و فاصله جسم تا سطح زمین است.
همانطور که مشاهده میشود، با افزایش فاصله از سطح زمین، مقدار شتاب جاذبه کاهش یافته است.
محاسبه جرم سیاره با دانستن شتاب جاذبه و شعاع آن
شتاب جاذبه سیاره برابر ۷/۵ متر بر مجذور ثانیه و شعاع آن برابر متر است. جرم این سیاره چه مقدار است؟
پاسخ: شتاب جاذبه با استفاده از رابطه زیر بهدست میآید:
در این مثال، مقدار M را باید بهدست آوریم.
با جایگذاری مقدارهای داده شده در رابطه فوق، مقدار جرم سیاره برابر کیلوگرم بهدست میآید.
محاسبه مقدار نیروی جاذبه بر روی سطح زمین
اگر جرم جسمی برابر ۱۰۰۰ کیلوگرم بر روی سطح زمین باشد، مقدار نیروی جاذبه وارد شده از سمت زمین بر آن را بهدست آورید. جرم زمین برابر کیلوگرم و شعاع آن برابر متر است.
پاسخ: دادههای پرسش عبارت هستند از:
- جرم زمین برابر است.
- جرم جسم برابر ۱۰۰۰ کیلوگرم است.
- شعاع زمین برابر است.
- ثابت جهانی گرانش برابر است.
- شتاب جاذبه در سطح زمین برابر ۹/۸ متر بر مجذور ثانیه است.
نیروی جاذبه را به صورت زیر بهدست میآوریم:
از آنجایی که جسم بر روی سطح زمین قرار گرفته است، r برابر شعاع زمین خواهد بود. با جایگذاری مقدارهای داده شده در رابطه نیرو، داریم:
توجه به این نکته مهم است که نیروی جاذبه وارد شده از طرف زمین بر جسمی در نزدیکی سطح آن، برابر وزن جسم خواهد بود. بنابراین، وزن جسم ۱۰۰۰ کیلوگرمی در سطح زمین برابر 9778 نیوتن است. خالی از لطف نیست که وزن جسم را با استفاده از رابطه W=mg بهدست آوریم:
محاسبه نیروی جاذبه در ارتفاع مشخصی از سطح زمین
نیروی جاذبه وارد شده بر جسمی به جرم ۱۰۰۰ کیلوگرم در ارتفاع ۱۰ هزار متری از سطح زمین را بهدست آورید. جرم زمین برابر و شعاع آن برابر است.
پاسخ: گفتیم مقدار نیروی جاذبه با افزایش فاصله دو جسم از یکدیگر کاهش مییابد. در نتیجه، مقدار جاذبه وارد شده بر جسم در ارتفاع داده شده کمتر از این نیرو بر روی سطح زمین است. مقدار این نیرو برابر است با:
با مقایسه وزن محاسبه شده بر روی سطح زمین و در ارتفاع ده هزار کیلومتری از آن، مقدار وزن به اندازه ۰/۲۳ درصد کاهش یافته است.
محاسبه وزن فضاپیما
وزن فضاپیمایی برابر w است. اگر قطر زمین D باشد، وزن این فضاپیما را در ارتفاع 2D از سطح زمین بهدست آورید.
پاسخ: اگر شعاع زمین برابر R باشد، 2D برابر 4R خواهد بود. در ابتدا با استفاده از رابطه نیروی جاذبه، وزن فضاپیما را بر روی سطح زمین محاسبه میکنیم:
اکنون وزن فضاپیما را در ارتفاع 2D از سطح زمین بهست میآوریم:
با توجه به محاسبات بالا، وزن فضاپیما در ارتفاع 2D از سطح زمین وزن آن در سطح زمین است.
مقایسه وزن جسم در دو سیاره
نسبت وزن سیاره A به سیاره B برابر ۲:۳ و نسبت شعاع این دو سیاره نسبت به یکدیگر برابر ۱:۲ است. اگر وزن جسمی بر روی سیاره A برابر W باشد، وزن جسم در سیره B چه مقدار خواهد بود؟
پاسخ: مقدارهای داده شده عبارت هستند از:
- جرم سیاره A = = ۲
- جرم سیاره B = = ۳
- شعاع سیاره A () = ۱
- شعاع سیاره B () = ۲
- جرم جسم = m
- وزن جسم بر روی سیاره A = W
باید وزن جسم بر روی سیاره B را بهدست آوریم:
وزن جسم بر روی سیاره A برابر است با:
وزن جسم B بر روی سیاره B برابر است با:
جرم جسم یکسان است، بنابراین m را با جایگزین میکنیم.
شتاب جاذبه در سطح ماه
شتاب جاذبه در سطح ماه را بهدست آورید. جرم ماه برابر و شعاع آن برابر متر است.

پاسخ: معادله قانون دوم حرکت نیوتن عبارت است از:
فرمول قانون جهانی گرانش نیوتن عبارت است از:
رابطه نوشته شده برای نیروی F را در رابطه نوشته شده برای g میگذاریم:
در ادامه، شتاب جاذبه در سطح ماه را بهدست میآوریم:
سقوط جسم در سیاره ای دلخواه
فرض کنید جسمی با سرعت اولیه صفر در نزدیکی سطح سیاره بزرگ آلفا رها ميشود و مسافت ۱۳/۵ متر را در ۳ ثانیه طی میکند. اگر شعاع این سیاره برابر متر باشد، مطلوب است:
- شتاب سقوط جسم
- جرم سیاره آلفا
پاسخ: در ابتدا، شتاب سقوط جسم را بهدست میآوریم:
ارتفاع سقوط و مدت زمان آن داده شده است. بنابراین، با استفاده از فرمول مسافت در حرکت با شتاب ثابت، شتاب سقوط را محاسبه میکنیم:
در ادامه، جرم سیاره را بهدست میآوریم. R شعاع سیاره، جرم سیاره و جرم جسم هستند. جسم به دلیل نیروی جاذبه شتاب میگیرد، بنابراین این نیرو را برابر حاصلضرب جرم جسم در شتاب حرکت آن قرار میدهیم.
حرکت ماهواره به دور زمین
ماهوارهای به جرم ۱۵۰۰ کیلوگرم در ارتفاع متری از سطح زمین به دور آن میچرخد.
- سرعت چرخش ماهواره چه مقدار است؟
- دوره تناوب حرکت ماهواره را بهدست آورید.
- انرژی جنبشی ماهواره را بهدست آورید.

پاسخ: در ابتدا، سرعت چرخش ماهواره را بهدست میآوریم. برای آنکه ماهواره در مدار خود باقی بماند، نیروی مرکزگرای باید با نیروی جاذبه برابر باشد.
نیروی مرکزگرا به صورت زیر نوشته میشود:
در رابطه فوق، سرعت حرکت ماهواره، m جرم و R شعاع مدار آن هستند.
شعاع مدار حرکت ماهواره برابر جمع شعاع زمین و ارتفاع ماهواره از سطح زمین است.
نیروی جاذبه برابر است با:
با مساوی قرار دادن دو نیروی مرکزگرا و جاذبه، سرعت حرکت ماهواره را بهدست میآوریم:
برای به دست آوردن دوره تناوب حرکت ماهواره، به صورت زیر عمل میکنیم:
در پایان، انرژی جنبشی ماهواره را بهدست میآوریم:
برآیند نیروی جاذبه
فضاپیمایی بر روی خط مستقیمی بین زمین و ماه قرار گرفته است. در چه فاصلهای از مرکز زمین، نیروی جاذبه کل بر روی این فضاپیما برابر صفر است؟ جرم زمین برابر ، جرم ماه برابر و فاصله بین مرکز ماه تا زمین برابر d است.
پاسخ: فضاپیما بر روی خط مستقیمی بین ماه و زمین قرار دارد.
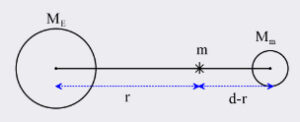
فرض کنید در نقطه r از مرکز زمین، برآیند نیروهای جاذبه وارد شده بر فضاپیما برابر صفر میشود. فضاپیما در فاصله میان ماه و زمین قرار گرفته است. بنابراین، از طرف ماه و زمین نیروی جاذبه بر آن وارد میشود.
باید r را بر حسب کمیتهای دیگر بهدست آوریم. با مرتبسازی رابطه بالا، داریم:
با قرار دادن و داریم:
معادله بهدست آمده معادلهای درجه دو بر حسب x است که باید ریشههای آن را با محاسبه دلتا بهدست آوریم:
پس از جایگذاری کمیتهای q و x داریم:
کاهش شتاب جاذبه با فاصله گرفتن از سطح سیاره ای دلخواه
سیارهای کروی به شعاع R و جرم M را در نظر بگیرید. شتاب جاذبه در چه فاصلهای از سطح سیاره، یکدهم مقدار آن بر روی سطح سیاره میشود؟
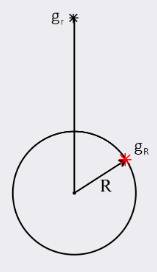
پاسخ: شتاب جاذبه جسمی به جرم m و در فاصله r از مرکز، برابر با است. به دنبال فاصلهای از مرکز سیاره هستیم که در آن فاصله، شتاب جاذبه مقدار آن در سطح سیاره شود:
از طرفین رابطه بالا، جذر میگیریم:
دو مقدار برای r بهدست آمده است که یکی از آنها قابل قبول نخواهد بود. مقدار اول r عبارت است از:
مقدار دوم r است با:
مقدار دوم برای r پذیرفته شده نیست، زیرا منفی است.
نیرو و پتانسیل گرانشی ناشی از حلقه ای به جرم M
حلقهای به جرم M و شعاع a در نظر بگیرید.
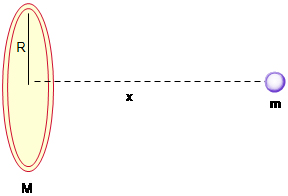
ذرهای به جرم m در فاصله x از مرکز حلقه قرار گرفته است.
- انرژی پتانسیل گرانشی این سیستم را بهدست آورید. هنگامی که دو جسم در فاصله بسیار دوری از یکدیگر قرار دارند، انرژی پتانسیل را برابر صفر در نظر بگیرید. به این نکته توجه داشته باشید که که در آن h است. انرژی پتانسیل کل برابر انتگرال dU بر روی حلقه است.
- نشان دهید جواب بهدست آمده در قسمت ۱، در فاصلههایی بسیار بزرگتر از شعاع حلقه، مشابه حالت جرمهای نقطهای میشود.
- با استفاده از بزرگی و جهت نیروی وارد شده بر ذره را بهدست آورید.
- نشان دهید نیروی بهدست آمده در قسمت ۳، در فاصلهای بسیار بزرگتر از شعاع حلقه، مشابه نیروی بین جرمهای نقطهای خواهد شد. مقدارهای U و را در x=0 بهدست آورید.
پاسخ: در ابتدا قسمت یک را حل میکنیم. انرژی پتانسیل گرانشی دو ذره نقطهای به جرمهای m و M که در فاصله r از هم قرار گرفتهاند برابر است با:
برای بهدست آوردن انرژی پتانسیل گرانشی بین حلقه و جرم m، حلقه را به قطعههای کوچکی به جرم dM تقسیم میکنیم. انرژی پتانسیل بین جرم m و یکی از قطعههای حلقه برابر است با:
انرژی پتانسیل کل به صورت زیر بهدست میآید:
قسمت ۲: اگر باشد، با استفاده از بسط چند جملهای داریم:
قسمت ۳: برای بهدست آوردن نیروی جاذبه بین حلقه و جرم m، از انرژی پتانسیل مشتق میگیریم:
اگر فرض کنیم که :
قسمت ۴: در این قسمت انرژی پتانسیل و نروی جاذبه را در مرکز حلقه بهدست میآوریم:
مقایسه نیروی جاذبه در سیارات مختلف
گرانش یا نیروی جاذبه یکی از نیروهای بنیادی فیزیک است. موجودات طی میلیاردها سال در محیط زمین تکامل یافتهاند و به زندگی تحت کشش یا جاذبه ۹/۸ متر بر مجذور ثانیه عادت کردهاند. نیروی جاذبه برای کسانی که به فضا رفتهاند یا به ماه سفر کردهاند، بسیار گرانبها و از نظر کششی ضعیف است.
بزرگی این نیرو به جرم، اندازه و چگالی جسم بستگی دارد. بنابراین، با تغییر این سه کمیت، مقدار نیروی جاذبه تغییر خواهد کرد. به عنوان مثال، سیارههای منظومه شمسی از نظر اندازه و جرم متغیر هستند، در نتیجه بزرگی جاذبه در سطح آنها از سیارهای به سیاره دیگر به طور قابل ملاحظهای تغییر میکند.
به عنوان مثال، شتاب جاذبه در سطح زمین برابر ۹/۸۰ متر بر مجذور ثانیه است. بر طبق قانون جهانی گرانش که توسط نیوتن بیان شد، نیروی جاذبه متناسب با حاصلضرب جرم دو جسم است و با مجذور فاصله بین آنها نسبت عکس دارد.
جاذبه در سطح سیاره تیر چقدر است ؟
شعاع این سیاره به طور تقریب برابر ۲۴۴۰ کیلومتر و جرم آن برابر کیلوگرم است. اندازه این سیاره در حدود ۰/۳۸۳ برابر اندازه زمین و جرم آن ۰/۰۵۵ جرم زمین است. سیاره تیر کوچکترین و کمجرمترین سیاره در منظومه شمسی است. اما چگالی این سیاره بسیار بزرگ و در حدود و کمی کوچکتر از چگالی زمین یعنی است. شتاب جاذبه سطحی در نزدیکی سطح سیاره تیر برابر تخمین زده میشود. g برابر شتاب جاذبه در سطح زمین است.

جاذبه در سطح ماه چقدر است ؟
براساس محاسبات انجام شده، شتاب جاذبه سطحی ماه برابر است.
جاذبه در سطح سیاره مریخ چقدر است ؟
مریخ نیز از بسیاری جهتها شبیه زمین است، اما اندازه این سیاره در برابر زمین بسیار کوچکتر و جرم آن ۰/۱۰۷ برابر جرم زمین است. شتاب جاذبه سطحی مریخ در مقایسه با اندازه این کمیت در سطح زمین کوچکتر و برابر ۳/۷۱۱ متر بر مجذور ثانیه تخمین زده میشود.
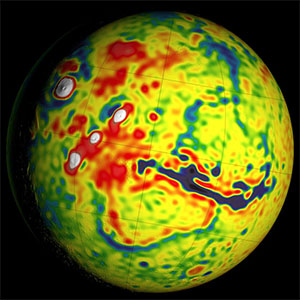
اگر مریخ را کرهای مسطح و با چگالی یکسان فرض کنیم، نیروی جاذبه وارد شده بر فضاپیما در همه جای این سیاره یکسان میبود. اما این سیاره نیز همانند زمین از پستیها و بلندیهای زیادی تشکیل شده است، بنابراین، نیروی جاذبه وارد شده از سمت مریخ بر فضاپیمای چرخان به دور آن، به آهستگی تغییر خواهد کرد. به عنوان مثال، اندازه این نیرو بر روی کوه مقداری بیشتر و در درهها کمی ضعیفتر است.
دانشمندان با استفاده از نوسانهای کوچک در دادههای مداری سه فضاپیمای ناسا، نقشه جدیدی از میدان گرانشی مریخ را رسم کردهاند.
جاذبه در سطح سیاره مشتری چقدر است ؟
سیاره مشتری، بزرگترین و سنگینترین سیاره در منظومه شمسی و جرم آن در حدود ۳۱۷/۸ برابر جرم زمین است. اما از آنجایی که این سیاره غولپیکر از جنس گاز است، چگالی آن از زمین کمتر و برابر 1/326 گرم بر سانتیمتر مکعب تخمین زده میشود. همچنین، مشتری به دلیل گازی بودن، سطح مشخصی ندارد. در نتیجه، شتاب جاذبه سطحی این سیاره برابر است.

جاذبه در سطح سیاره زحل چقدر است ؟
زحل نیز همانند مشتری، سیارهای غولپیکر و از جنس گاز و جرم آن در حدود ۹۵/۱۵ برابر جرم زمین است. شتاب جاذبه سطحی زحل اندکی بیشتر از مقدار آن در سطح زمین و برابر ۱۰/۴۴ متر بر مجذور ثانیه است.
جاذبه در سطح سیاره اورانوس چقدر است ؟
اندازه سیاره اورانوس در حدود چهار برابر و جرم آن ۱۴/۵۳۶ برابر زمین است، اما با توجه به گازی بودن اورانوس، چگالی بسیار کمتری نسبت به زمین دارد. شتاب سطحی جاذبه به طور تقریب باربر ۸/۶۹ متر بر مجذور ثانیه است.
اینشتین و نیروی جاذبه
تاکنون با دیدگاه نیوتن در مورد گرانش یا نیروی جاذبه آشنا شدیم، اما اینشتین برای توضیح گرانش، رویکرد متفاوتی را انتخاب کرد. براساس یافتهای این فیزیکدان، گرانش و شتاب مشابه یکدیگر هستند. برای توضیح بیشتر دیدگاه اینشتین، به داستانی که او برای توضیح نظریه خود استفاده کرد توجه کنید.
ستارهشناسی بدون هیچ خاطرهای در مورد گذشته، در فضاپیما از خواب بیدار میشود. او در حالی که به تنهایی بر روی صندلی نشسته است از خود میپرسد: من کجای این جهان هستم؟
فضاپیما هیچ پنجرهای ندارد و تمام وسایل آن از کار افتادهاند. تنها سرنخ، فشار صندلی به بدن او است، بنابراین با خود فکر میکند که نیروی جاذبه وجود دارد، پس فضاپیما باید روی زمین باشد. ناگهان فکر دیگری به ذهنش میرسد. شاید فضاپیما با شتاب در فضا حرکت میکند و او را به صندلی فشار میدهد (مانند ماشین مسابقهای که سرعتش زیاد میشود).
این معما و معضلِ فضانورد برای اینشتین آشنا بود. در سال ۱۹۱۵، نظریه نسبیت عام این فیزیکدان بر این مبنا پایهگذاری شد که شتاب و گرانش نه تنها به راحتی با یکدیگر اشتباه گرفته میشوند، بلکه مشابه یکدیگر هستند. این همارزی، نقطه شروعی برای تعریف مجدد گرانش یا نیروی جاذبه بود.
بر طبق نظریه نسبیت، هر چیزی که در جعبهای شتابدار رخ میدهد، در حضور گرانش نیز اتفاق خواهد افتاد. به عنوان مثال، آسانسوری را در نظر بگیرید که با شتاب مشخصی به سمت بالا حرکت میکند و لیزر افقی در آن قرار گرفته است. نور لیزر به طرفین حرکت میکند،. به هنگام بالا رفتن آسانسور، نور لیزر به نقطهای روی دیوار اندکی پایینتر از نقطه آغازین برخورد خواهد کرد. اگر آسانسور به اندازه کافی شتاب بگیرد، پرتو لیزر به سمت کف آسانسور خم میشود.
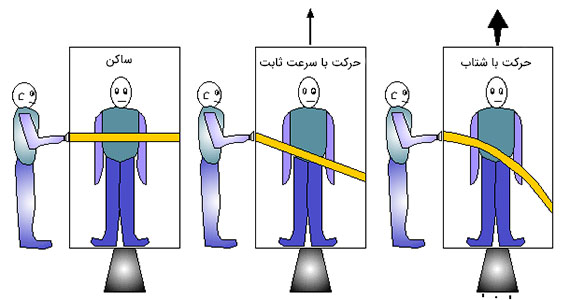
اینشتین نشان داد که اتفاق مشابهی برای پرتو لیزر داخل آسانسور ساکن در میدان گرانشی قوی، میافتد. در این حالت، گرانش یا جاذبه نور را خم میکند. او انتظار داشت که پرتو نور مستقیم به هنگام عبور از جاذبه خورشید، خم شود. این پیشبینی در سال ۱۹۱۹ ثابت شد.
همانطور که گفتیم نیوتن نیروی جاذبه یا گرانش را به صورت نیرو توصیف کرد. او فرض کرد که گرانش همانند طنابی است که اجسام با جرمهای مختلف را به سمت یکدیگر میکشد. معادلات بهدست آمده توسط نیوتن به خوبی حرکت سیارهها و حرکت پرتابی هر جسمی بر روی سطح زمین را توصیف کرد، اما در این معادلهها، نیروی جاذبه و شتاب جدا در نظر گرفته شدند. اینشتین در این مورد مخالف نیوتن بود. از نظر او، جاذبه نیرو نیست. او جاذبه را به صورت انحنای زمان و فضا در نظر گرفت.
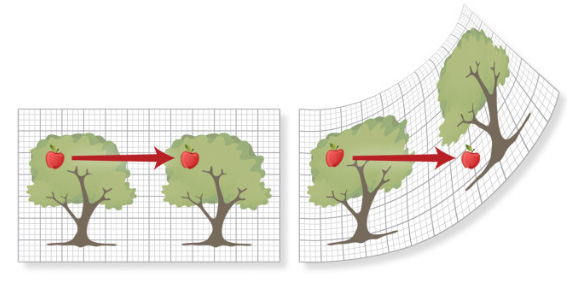
انحنای فضا و زمان در نگاه اول بسیار عجیب و غیرقابل فهم به نظر میرسد. حتی این عبارت برای اینشتین نیز سخت و برای توصیف این نظریه در حدود یک دهه درگیر بود. او برای توضیح انحنای فضا-زمان از ریاضیدانی به نام «مارسل گروسمن» (Marcel Grossmann) کمک گرفت. گروسمن دوست دوران مدرسه اینشتین بود که به هنگام فرار او از مدرسه، یادداشتهای درسی را به اینشتین میرساند.
ریاضیات نوشته شده برای گرانش از ده معادله تشکیل شد و در مورد چگونگی حرکت گرانش به دور اجسام توضیح میداد. به تصویر نشان داده شده در بالا توجه کنید. اگر سیب، نیرویی احساس نکند، در جای خود باقی میماند (شکل سمت چپ). اما هنگامی که گرانش سبب انحنای فضا و زمان میشود (شکل سمت راست)، سیب بدون حس کردن نیرویی بر روی زمین میافتد.
نکته های اصلی نسبیت عام اینشتین
اینشتین در بیان نظریه نسبیت عام، سه نکته اصلی را در نظر گرفت:
- فضا و زمان نه تخت هستند و نه ثابت. آنها توسط جرم و انرژی خم میشوند.
- جاذبه نیرو نیست، بلکه انحنای فضا و زمان است.
- در یک فضای کوچک، اثرات جاذبه و شتاب از یکدیگر قابل تشخیص نیستند.
پیش بینی های عجیب اینشتین
نسبیت پیشبینیهای عجیبی انجام داده است که بسیاری از آنها به طور تجربی ثابت شدهاند. این پیشبینیها از آن جهت عجیب هستند که آنها را در زندگی روزمره مشاهده نکردهایم. در واقع، زندگی خود را بیشتر در دنیای قوانین نیوتن سپری کردهایم. فراتر از قانونهای حرکت نیوتن، وارد جهان توصیف شده توسط اینشتین میشویم. در این جهان، گرانش، فضا و زمان را خم میکند. در ادامه، به چند نمونه از اثرهای جانبی عجیب این نظریه اشاره میکنیم.
جاذبه، زمان را کند میکند
امواج نوری تابیده شده توسط ستارگان به دلیل خم شدگی زمان، کش میآیند. اجسام نزدیکتر به جسمی سنگین، کندتر پیر میشوند. به بیان دیگر، دو فرد همسن را در نظر بگیرید. یکی از این افراد را در میدان جاذبه بسیار قوی قرار میدهیم. از آنجایی که زمان در میدان گرانش کند میشود، فرد قرار داده شده در نزدیکی جاذبه قوی، کندتر گذر زمان را حس خواهد کرد. این پیشبینی با استفاده از ساعتهای بسیار دقیق اثبات شده است. عملکرد این ساعتها براساس ارتعاش اتمها است.
به طور حتم فیلم «میانستارهای» را تماشا کردهاید و با خود اندیشیدهاید که چگونه چنین چیزی ممکن است. فکر کردن به این موضوع که گذر یک ساعت در یک سیاره معادل هفت سال بر روی زمین است، کمی گمراهکننده به نظر میرسد. برای توضیح این حالت از اتساع زمان استفاده میشود.

دو ناظر را در نظر بگیرید که در فاصلههای متفاوتی از جرم گرانشی دلخواهی قرار گرفتهاند. این دو ناظر فاصله زمانی بین دو رویداد را اندازه میگیرند. بر طبق اتساع زمانی گرانشی، زمانهای اندازهگیری شده توسط این دو ناظر یکسان نخواهد بود. به بیان دیگر، هر جایی که جاذبه قویتر باشد، زمان کندتر سپری میشود. دلیل این امر آن است که گرانش فضا-زمان را خم میکند.
به رابطه زیر دقت کنید:
نور همواره با سرعت ثابت ۳۰۰ هزار متر بر ثانیه حرکت میکند. دو پرتو نور را در نظر بگیرید. نور شماره یک در میدان گرانشی ضعیفی قرار دارد و بین دو نقطه a و b حرکت میکند. نور دوم در میدان گرانشی قویتری قرار گرفته است و بین دو نقطه c و d حرکت میکند.
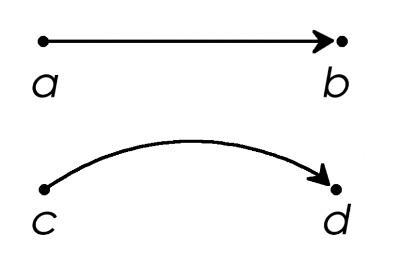
مسیر بین دو نقطه c و d به دلیل انحنای فضا و زمان طولانیتر است، بنابراین نور در مدت زمان بیشتری از نقطه c به d خواهد رفت. این اثر با استفاده از آزمایشهای تجربی بسیاری به اثبات رسیده است و بیشتر ما از این اثر، روزانه تحت عنوان GPS، استفاده میکنیم.
ماهوارههای «سیستم موقعیتیاب جهانی» (Global Positioning System | GPS) در فاصلهای در حدود ۲۰۲۰۰ کیلوکتر از سطح زمین قرار گرفتهاند، بنابراین به میدان گرانشی زمین خیلی نزدیک نیستند. عقربه ساعتهای قرار گرفته در این ماهواره نسبت به ساعتهای قرار گرفته بر روی زمان، سریعتر حرکت میکنند. بنابراین، دانشمندان بهمنظور اطمینان از تشابه زمانی دادههای ارسالی توسط GPS به سطح زمین، اصلاحاتی را بر روی برنامههای ماهوارهای قرار میدهند. GPS بدون این اصلاحات، وسیله مناسبی برای استفاده نخواهد بود.

بسیاری از انسانها به دنبال یافتن راهی برای زندگی طولانیتر هستند. شاید به این فکر کنید که سفر به سیارهای دور با میدان گرانشی قویتر، به شما در تحقق این آرزو کمک خواهد کرد. توجه به دو نکته در اینجا مهم است. نخست آنکه سفر به سیارهای دوردست با تکنولوژی امروز امکانپذیر نیست. دوم، حتی اگر بتوانید این سفر را انجام دهید، عمر شما نسبت به ناظران روی زمین طولانیتر خواهد بود و نباید فراموش کنید که طول عمر انسان در حال حاضر بین ۷۰ تا ۱۰۰ سال است. ناظر در نسبیت، نقش مهمی را ایفا میکند.
منظومه شمسی را در نظر بگیرید. سیاره مشتری بیشترین جرم را در مقایسه با سیارههای دیگر دارد، بنابراین میدان گرانشی آن در مقایسه با دیگر سیارهها قویتر است. شاید دوست داشته باشید که بدانید در صورت سفر به مشتری و زندگی بر روی این سیاره، چند سال بیشتر نسبت به زمین زندگی خواهید کرد. جواب به این پرسش در حد چند دقیقه است.
کندی زمان در نزدیکی میدان گرانشی قوی را کمی با جزئیات بیشتری بیان میکنیم. بر طبق نظریه بیان شده توسط نیوتن، سرعت کمیتی نسبی است. به عنوان مثال، سرعت ماشینی که با سرعت ۹۰ کیلومتر بر ساعت حرکت میکند نسبت به ناظری ساکن سنجیده شده است. اما سرعت این ماشین نسبت به ماشینی دیگری که با سرعت ۵۰ کیلومتر بر ثانیه حرکت میکند برابر ۴۰ کیلومتر بر ساعت خواهد بود. مفهوم سرعت نسبی با نظریه ماکسول ناسازگار بود. این ناسازگاری اینشتین را با دوراهی دردناکی روبرو کرد.
این تناقض سبب شد که اینشتین یکی از متحیرانهترین و عجیبترین ادعاهای مطرح شده در علم فیزیک را بیان کند. برای درک بهتر این تناقض و چرایی آهسته شدن زمان، آزمایش فکری مبتکرانه زیر را در نظر بگیرید.
فردی را در ایستگاه قطار در نظر بگیرید که در دو طرف او دو رعد و برق زده میشوند. اگر دو نقطهای که رعد و برق با آن برخورد میکند را a و b در نظر بگیریم، این فرد درست در وسط خط متصل کننده این دو نقطه ایستاده است و نور ناشی از رعد و برق را در زمان یکسانی مشاهده میکند. اما ناظر سوار بر قطاری که با سرعت نور حرکت میکند، این صحنه را متفاوت و عجیب خواهد دید.
بر طبق قوانین حرکت، نورِ صاعقه نزدیکتر به قطار نسبت به نور صاعقهای که از قطار دورتر است، زودتر به ناظر داخل قطار خواهد رسید. این دو فرد سرعت نور را اندازه میگیرند و عددهای متفاوتی را بهدست میآورند. در اینجا به تناقض میخوریم، زیرا بر طبق نظریه ماکسول، سرعت نور باید ثابت باشد.
برای جبران و رفع این تناقض، اینشتین پیشنهاد داد که زمان کند میشود و در نتیجه سرعت نور ثابت خواهد ماند. زمان برای فردی که در قطار است نسبت به فردی که در ایستگاه ایستاده است، آهستهتر میگذرد.
اجرام آسمانی چرخان، کیهان را به دور خود میچرخانند
در مطالعهای که در سال ۲۰۲۰ انجام شد، چگونگی چرخش فضا و زمان به دور ستارهای مرده مشخص و تایید شد. اینشتین پیشبینی کرده بود که فضا و زمان به دور جسمی بزرگ و چرخان، میچرخند. به عنوان مثال، فرض کنید زمین در عسل غوطهور شده است. اگر زمین بچرخد، عسل قرار گرفته در اطراف آن نیز خواهد چرخید. این مثال ساده برای چرخش فضا و زمان به دور جسمی بزرگ با جرم زیاد نیز صادق است.
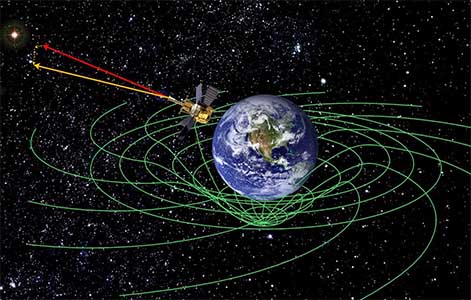
آزمایشهای ماهوارهای، کشش فضا و زمان را در میدان گرانشی زمین آشکار کردهاند، اما این اثر به اندازهای کوچک است که اندازهگیری آن با چالش بسیاری روبرو خواهد شد. اجسامی با جرمهای بزرگتر و میدانهای گرانشی قویتر، مانند کوتولههای سفید و ستارههای نوترونی، محل بهتری برای دیدن این پدیده هستند. از این رو، دانشمندان بر روی تپاختری به نام PSRJ1141-6545 تمرکز کردند. جرم این تپاختر در حدود ۱/۲۷ برابر جرم خورشید است و در فاصله ۱۰۰۰۰ تا ۲۵۰۰۰ سال نوری از زمین قرار گرفته است.
تپاختر ستاره نوترونی است که با سرعت بسیار زیاد میچرخد و امواج رادیویی را در امتداد قطبهای مغناطیسی خود ساطع میکند. تپاختر PSRJ1141-6545 به دور کوتولهای سفید با جرمی در حدود جرم خورشید، میچرخد. تپاختر در مداری فشرده و بسیار سریع (کمتر از ۵ ساعت) به دور کوتوله سفید میچرخد.
دانشمندان پالسهای دریافت شده از تپاختر را با دقت ۱۰۰ میکروثانیه در مدت زمانی در حدود ۲۰ سال با استفاده از تلسکوپهای رادیویی اندازه گرفتند. با استفاده از این اندازهگیری، انحرافی در مسیر چرخش کوتوله سفید و تپاختر به دور یکدیگر شناسایی شد. دانشمندان با حذف تمام علتهای ممکن برای رخ دادن این انحراف، به این نتیجه رسیدند که انحراف در نتیجه کشیدگی فضا-زمان رخ میدهد. کوتوله سفید با سرعت زیادی در حال چرخش است و سبب کشیدگی فضا-زمان میشود، بنابراین جهت مدار تپاختر به آهستگی در طول زمان تغییر خواهد کرد.
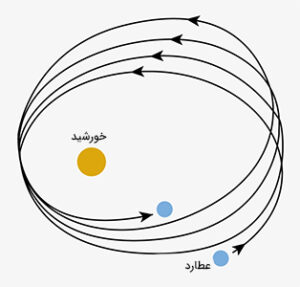
تکانی کوچک در مدار عطارد
یکی از پیشبینیهای اینشتین، معمایی دیرینه را حل کرد. در مدار عطارد، تکان کوچکی مشاهده شد. نیوتن این تکان را به نیروی جاذبه ناشی از سیارهای دیگر به نام ولکان ربط داد. اما اینشتین نظر دیگری در مورد معمای مدار عطارد داشت. نظریه نسبیت عام توانست حرکت عطارد به دور خورشید را با دقت بسیار بالایی توصیف کند.
موج های کوچک در واقعیت
در سالهای بسیار دور، دو سیاه چاله با جرمهای بسیار سنگین، به آرامی به یکدیگر نزدیک شدند، تا اینکه در حدود ۱/۳ میلیارد سال قبل در حالیکه با سرعتی برابر نصف سرعت نور به دور یکدیگر میچرخیدند، با هم ادغام شدند. در اثر برخورد این دو سیاهچاله با یکدیگر، ارتعاشی در جهان ایجاد شد و موجکهایی به نام امواج گرانشی در فضا و زمان گسترش یافتند. در حدود ۶ سال قبل، این موجکها از اطراف زمین عبور کردند و فیزیکدانها برای نخستین بار این امواج را شناسایی کردند.
پرسش های جالب در مورد نیروی جاذبه
تاکنون با نیروی جاذبه یا همان گرانش آشنا شدیم. در ادامه، به چند پرسش جالب در مورد این نیرو پاسخ میدهیم.
آیا گرانش میتواند به شکل موج باشد ؟
بله، گرانش میتواند به شکل موج باشد. امواج گرانشی موجکهایی در فضا-زمان هستند. اگر به گرانش به دید نیرویی وابسته به فاصله نگاه کنید، درکی از امواج گرانشی نخواهید داشت. اما اگر گرانش را با استفاده از نظریه نسبیت عام تفسیر کنید، درک این امواج برای شما بسیار آسانتر خواهد بود.
آیا وزن شما در استوا کمتر از قطب شمال است ؟
بله، وزن شما در استوا کمتر از مقدار آن در قطب شمال یا جنوب است. توجه به این نکته مهم است که جرم شما تغییر نمیکند. در واقع، مقدار نیروی جاذبه با نزدیک شدن به قطبها تغییر خواهد کرد. وزن شما ترکیبی از تمام نیروهای بزرگمقیاس بر روی بدن شما است. جاذبه زمین تنها نیروی بزرگمقیاس نیست. نیروهای بزرگمقیاس دیگری مانند جاذبه خورشید، جاذبه ماه و نیروی مرکزگرای زمین نیز بر اندازه وزن تاثیر میگذارند. اگر زمین کرهای مسطح بود، نیروی جاذبه در همه جای آن یکسان میبود، اما مقدار این نیرو از نقطهای به نقطه دیگر بر روی سطح زمین به مقدار بسیار جزیی، تغییر میکند.
نیروی جاذبه تا چند کیلومتری زمین است ؟
در فضا و در همه جا جاذبه وجود دارد. هر چه از زمین دورتر شویم، مقدار نیروی جاذبه ضعیفتر خواهد شد، اما نرخ میرایی این نیرو در مقایسه با نیروهای هستهای بسیار کوچکتر است. هنگامی که در فضا به سیاره دیگری نزدیک میشویم، جاذبه آن بر جاذبه زمین غلبه خواهد کرد. تنها در این حالت میتوان از جاذبه زمین چشمپوشی کرد. به دو علت نیروی جاذبه را در فضا حس نمیکنیم:
- فضا بسیار بزرگ و نسبت به استانداردهای زمین، به نسبت تهی است. به هنگام پرش از روی پل، سقوط را با عبور جریان هوا یا دیدن کوهها، احساس خواهیم کرد. همچنین، پس از مدت زمان کوتاهی بر روی زمین فرود میآییم. اما مقدار هوا در فضا بسیار اندک است و به دلیل بزرگی آن، سقوط ممکن است ساعتها یا سالها ادامه یابد.
- در فضا، اجسام به جای برخورد با سیارهها، تمایل به چرخش به دوره آنها دارند. در نتیجه، نیروی جاذبه احساس نمیشود.













ممنون از توضیحات شما
همیشه با خودم فکر میکنم ای کاش درک وفهم ما انسانها از جهان هستی مانند بقیه موجودات در حد ناچیز بود ویا هم درک بالاتری میداشتیم که لااقل ذره ای از جهان هستی رو بتونیم درک کنیم و اینقدر ناتوان نباشیم .
خیلی هم به زبان ساده بود!!!واقعا که !بازهم هیچی نگرفتم!
با سلام ک تشکر از مطلب خوب شما.
در بخش محاسبه نیروی جاذبه زمین،به جای جرم زمین نوشتید: شعاع زمین برابر 24**10×5.98 کیلوگرم است.
با تشکر.
با سلام؛
مطلب بازبینی و اصلاح شد.
با تشکر از همراهی شما با مجله فرادرس