انبساط گرمایی – به زبان ساده

انبساط گرمایی (Thermal Expansion) به توانایی ماده در تغییر حجم،‌ طول و مساحت در مقابل تغییر دمای ماده گفته می‌شود. دما در حقیقت معیاری از میزان حرکت‌ مولکول‌های یک ماده است. در ادامه در مورد علت وجود انبساط گرمایی و ارتباط آن با دما بحث خواهد شد.

مقدمه

انبساط الکل در یک ترمومتر،‌ نمونه‌ای از انبساط گرمایی محسوب می‌شود. از طرفی افزایش حجم اندک فولاد در نتیجه افزایش دما نیز پدیده‌ای مشابه است. حرکت کردن هوای داغ به سمت بالا نیز به دلیل انبساط گرمایی رخ می‌دهد. در حقیقت هوای گرم منبسط شده، چگالی آن کم شده و به دلیل وجود نیروی شناوری به سمت بالا حرکت می‌کند.

شاید برای شما نیز این سوال پیش آمده باشد که چرا افزایش دما منجر به افزایش حجم مواد می‌شود؟ پاسخ در انرژی جنبشی اتم‌های ماده است. همان‌طور که در بالا نیز بیان شد، دمای یک جسم معیاری از انرژی جنبشی اتم‌های آن است. بنابراین با افزایش دمای ماده،‌ میانگین انرژی جنبشی اتم‌های آن نیز افزایش خواهند یافت. با افزایش انرژی جنبشی، اتم‌ها به یکدیگر نیرو وارد کرده، بنابراین در فاصله‌ای بیشتر از هم قرار می‌گیرند. این افزایش فاصله منجر به انبساط کل ماده خواهد شد.

در مواد جامد برخلاف مایعات و گاز‌ها، اتم‌های ماده به یکدیگر نزدیک بوده و به‌صورت بلوک هستند. با افزایش انرژی جنبشی اتم‌های ماده،‌ اتم‌های همجوار به یکدیگر نیرو وارد کرده و میانگین فاصله آن‌ها نیز افزایش خواهد یافت.

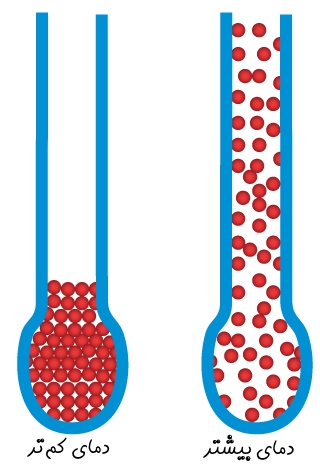
انبساط گرمایی خطی

معمولا به منظور ساده‌سازی شبیه‌سازی، افزایش طول ماده به‌صورت خطی، وابسته به طول اولیه در نظر گرفته می‌شود. در حقیقت تغییرات طول برای یک ماده را می‌توان به‌صورت زیر در نظر گرفت.

$$\large \Delta L=\alpha L \Delta T$$
رابطه ۱

فیلم آموزش فیزیک پایه ۳ – جامع و کاربردی در فرادرس

کلیک کنید

در رابطه فوق، $$\Delta$$ نشان دهنده تغییرات است (برای نمونه $$\Delta L$$ نشان دهنده تغییرات طول ماده است). از طرفی L طول اولیه و ΔT تغییرات دمایی را بیان می‌کند. هم‌چنین ضریب α عددی ثابت تحت عنوان ضریب انبساط خطی است. این ضریب در حقیقت بیان کننده افزایش طول ۱ متر از ماده به ازای افزایش دمای 1 کلوین است. جالب است بدانید که مقدار منفی برای این ضریب به معنای کاهش طول ماده با افزیش دما است. در جدول زیر ضریب انبساط خطی برخی از مهم‌ترین مواد بیان شده‌اند.

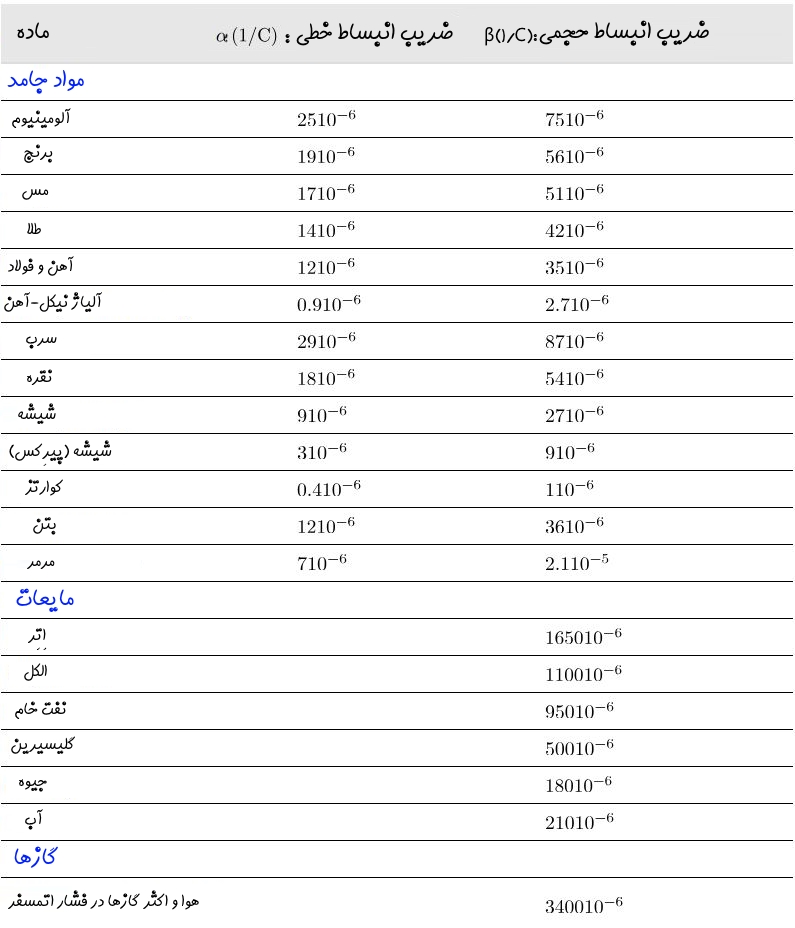
جدول بالا نشان می‌دهد می‌توان برای هر ترکیبی ضریب انبساط را تعریف کرد. حتی استخوان‌های بدن انسان نیز از پدیده‌ی انبساط گرمایی پیروی می‌کنند.

مثال ۱

فرض کنید پلی در شهری کویری قرار گرفته و طول آن برابر با ۱۲۷۵ متر است. با توجه به آب و هوای شهر، پل در معرض بازه‌ی دمایی بین ۱۵- و ۴۰ درجه‌ی سانتی‌گراد قرار می‌گیرد. با فرض این‌که ضریب انبساط طولی پل برابر با $$1210×10^{-8} \enspace \frac{1}{C}$$ باشد، اختلاف طول برج در سرد‌ترین و گرم‌ترین حالت چقدر است؟

می‌توان به سادگی و با استفاده از رابطه ۱، اختلاف طول را بدست آورد. توجه داشته باشید به‌منظور بدست آوردن تغییر طول ماده نیازی نیست تا طول اولیه آن را بدانیم. تغییرات طول در این مسئله نیز برابر است با:

$$\large \Delta L =\alpha L \Delta T=1210×1275×55×10^{-8}=0.84 \enspace m$$

بنابراین اختلاف طول پل در زمستان و تابستان نزدیک به ۱ متر است!

انبساط گرمایی دوبعدی و سه‌بعدی

بدیهی است که یک ماده در تمامی جهات تغییر طول می‌دهد. بنابراین مساحت و حجم یک ماده با نوسان دما، تغییر خواهد کرد. در نتیجه اگر سوراخی در جسم وجود داشته باشد، با افزایش دما اندازه آن نیز افزایش خواهد یافت. برای تغییرات اندک دما، تغییرات مساحت با استفاده از فرمول زیر بدست می‌آید.

$$\large \Delta A =2\alpha A \Delta T$$

در رابطه فوق $$\Delta A$$ نشان دهنده تغییر مساحت است. $$\alpha$$، ضریب انبساط خطی و $$\Delta T$$ نشان دهنده تغییرات دما است. بایستی توجه داشته باشید که A در سمت راست رابطه‌ی فوق نشان دهنده مساحت اولیه ماده است. معمولا ضرایب انبساط سطحی و حجمی به‌ترتیب دو و سه برابر ضریب انبساط حجمی در نظر گرفته می‌شوند (در رابطه فوق ضریب ۲ به همین دلیل ارائه شده).

در شکل زیر انبساط حجمی در حالت دوبعدی و سه‌بعدی نشان داده شده‌اند. خط‌چین نشان دهنده مرز‌های جسم پس از افزایش دما و خطوط پیوسته نشان دهنده شکل اولیه‌ی جسم است.

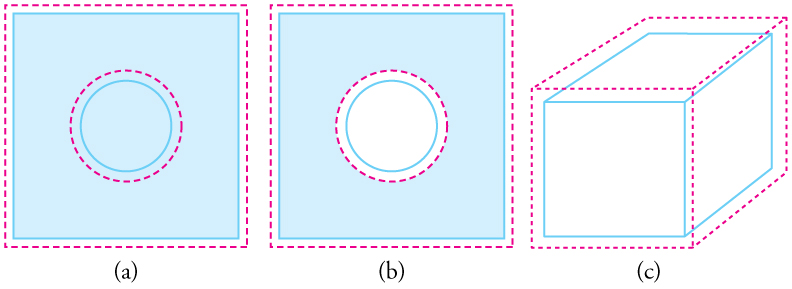
مشابه با حالت تک‌بعدی و دوبعدی می‌توان رابطه مربوط به افزایش حجمِ جسم را نیز با استفاده از رابطه‌ $$\Delta V=\beta V \Delta T$$ توصیف کرد. در رابطه فوق، $$\beta$$، ضریب انبساط حجمی است که مقدار آن نیز برابر با $$\beta=3 \alpha$$ در نظر گرفته می‌شود.

در حالت کلی نه تنها مواد جامد یا فلزات بلکه تمامی مواد انبساط گرمایی را تجربه خواهند کرد. مهم‌ترین استثناء این قانون آب است. به‌طور دقیق‌تر می‌توان گفت ویژگی‌های ترمودینامیکی آب به نحوی است که متفاوت با دیگر مواد رفتار می‌کند. در حقیقت در بازه‌ی بین ۰ تا ۴ درجه‌ی سانتی‌گراد، با افزایش دمای آب، چگالی آن نیز افزایش می‌یابد. از طرفی دلیل افزایش چگالی نیز کاهش حجم است. بنابراین در بازه مذکور با افزایش دمای آب، حجمش کاهش می‌یابد. در شکل زیر تغییرات چگالی آب بر حسب دما نشان داده شده است.

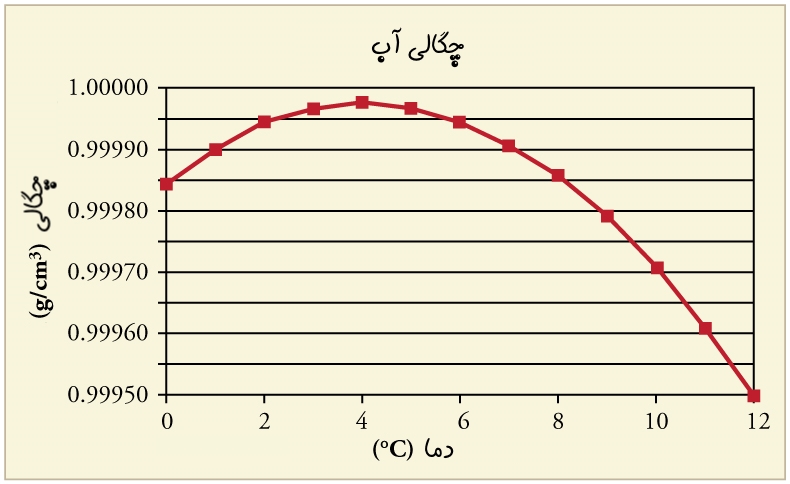
جالب است بدانید که انبساط سوخت و محفظه‌ی خودرو منجر به این امر می‌شود که گنجایش باک در زمستان و تابستان متفاوت باشد! هم‌چنین به‌دلیل افزایش چگالی هوا،‌ پرواز هواپیما در زمستان آسان‌تر خواهد بود.

مثال ۲

فرض کنید ظرفیت باک خودروی شما برابر با ۶۰ لیتر باشد. حال تصور کنید که این باک با سوخت ۱۵ درجه سانتی‌گراد پر شود. اگر دمای سوخت ورودی ۳۵ درجه باشد، حجم آن نیز منبسط شده و جرم کمتری از سوخت در باک قرار خواهد گرفت. مقدار حجم از دست رفته نسبت به دمای ۱۵ درجه، در حالتی که دمای سوخت و باک ۳۵ درجه شود، چقدر است؟ ضریب انبساط حجمی باک و سوخت را به‌ترتیب برابر با $$35×10^{-6} \frac {1}{C}$$ و $$950×10^{-6} \frac{1}{C}$$ در نظر بگیرید.

دمای باک و سوخت با هم افزایش یافته است. بنابراین حجم آن‌ها نیز افزایش خواهند یافت. اما نکته این جا است که افزایش حجم سوخت بیشتر از افزایش حجم باک است. در ابتدا افزایش حجم باک را مطابق با رابطه زیر بدست می‌آوریم.

$$\large \Delta V_{tank}=\beta_{tank} V_{tank} \Delta T$$

به همین شکل افزایش حجم سوخت برابر است با:

$$\large \Delta V_{Fuel}=\beta_{Fuel} V_{Fuel} \Delta T$$

اختلاف این دو حجم برابر با حجم از دست رفته است.

$$\large V_{Lost}=\Delta V_{Fuel}-\Delta V_{tank}$$

با جایگذاری ضرایب انبساط حجمی و حجم اولیه (حجم در دمای ۱۵ درجه)، اختلاف حجم سوخت وارد شده به باک برابر هستند با:

$$\large \begin{array}{lll}{V}_{\text{Lost}}& =& \left({\beta }_{\text{Fuel}}-{\beta }_{\text{tank}}\right)V\text{Δ}T\\ & =& \left[\left(\text{950}-\text{35}\right)×{\text{10}}^{-6}/\text{º}\text{C}\right]\left(\text{60}\text{.}0\phantom{\rule{0.25em}{0ex}}\text{L}\right)\left(\text{20}\text{.}0\text{º}\text{C}\right)\\ & =& 1\text{.}\text{10}\phantom{\rule{0.25em}{0ex}}\text{L}\end{array}$$

تنش‌ حرارتی

تنش‌های حرارتی در نتیجه تغییرات طول ناشی از نوسانات دما ایجاد می‌شوند. تنش حرارتی می‌تواند مخرب باشد. برای نمونه اگر محفظه‌ای از سوخت پر باشد، با گرم شدنش، سوخت درون مخزن منبسط شده و به دیواره‌های مخزن نیرو وارد می‌کند. در شکل زیر اثرات تنش‌های حرارتی، نشان داده شده‌اند.

در زیر مثالی به‌منظور نحوه ایجاد تنش حرارتی ارائه شده است.

مثال ۳

فرض کنید در مثال شماره ۲، مخزن در دمای ۱۵ درجه پر شده و ورودی آن بسته می‌شود. سپس کل مخزن به همراه سوخت تا دمای ۳۵ درجه گرم می‌شود. با فرض این‌که مدول بالک یا همان مدول حجمی برابر با $$1.0010^9 N/m^2$$ باشد، فشار ایجاد شده در مخزن را بیابید.

رابطه بین تغییرات حجم یک سیستم و فشار ایجاد شده در آن برابر است با:

$$\large \text{Δ}V=\frac{1}{B}\frac{F}{A}{V}_{0}$$

البته در این لینک به‌طور مفصل در مورد مدول بالک و مفاهیم مرتبط با آن بحث شده. در رابطه فوق $$\frac{F}{A}$$ نشان دهنده فشار ایجاد شده در مخزن است. بنابراین اگر این مقدار را با نماد P نشان دهیم، می‌توان آن را از رابطه فوق بدست آورد.

$$\large P=\frac{F}{A}=\frac{\text{Δ}V}{{V}_{0}}B\text{}$$

توجه داشته باشید که تغییر خالص حجم در مثال ۲ برابر با ۱.۱ لیتر بدست آمده. بنابراین نهایتا با جایگذاری مقادیر معلوم در رابطه فوق، فشار ایجاد شده در مخزن برابر با عدد زیر بدست می‌آید.

$$\large P=\frac{1\text{.}\text{10 L}}{\text{60}\text{.}\text{0 L}}\left(1\text{.}\text{00}×{\text{10}}^{9}\phantom{\rule{0.25em}{0ex}}\text{Pa}\right)=1\text{.}\text{83}×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}\text{Pa}\text{}$$

خلاصه

• انبساط گرمایی به تغییر طول،‌ مساحت و حجم مواد در نتیجه تغییرات دما اطلاق می‌شود.
• انبساط گرمایی در گاز‌ها به نسبت مواد جامد بیشتر است. البته نمی‌توان از انبساط گرمایی مواد جامد و مایعات نیز صرف‌نظر کرد.
• انبساط گرمایی خطی مطابق با رابطه $$\text{Δ}L=\mathrm{\alpha L}\text{Δ}T$$ بدست می‌آید. در این رابطه L,ΔL,α,ΔT به‌ترتیب نشان دهنده تغییر دما، ضریب انبساط خطی، تغییر طول و طول اولیه است.
• انبساط سطحی مطابق با رابطه $$\text{Δ}A=2\mathrm{\alpha A}\text{Δ}T$$ بدست می‌آید. در این رابطه ΔA نشان دهنده میزان انبساط سطحی است.
• تغییرات حجمی در نتیجه‌ی تغییرات دما نیز مطابق با رابطه $$\large \text{Δ}V=\mathrm{\beta V}\text{Δ}T$$ بدست می‌آید.
• معمولا ضرایب انبساط سطحی و حجمی به‌ترتیب دو برابر و سه‌ برابر ضریب انبساط خطی در نظر گرفته می‌شوند.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه‌ فیزیک و مهندسی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس فیزیک
• مجموعه آموزش‌های دروس مهندسی مکانیک
• مجموعه آموزش‌های ریاضی و فیزیک
• اوربیتال و آرایش الکترونی -- به زبان ساده
• سیم داغ یا هات وایر (Hot Wire) — از صفر تا صد