انرژی جنبشی چیست؟ — به زبان ساده

پیش از این در مجله فرادرس، پایستگی انرژی را بررسی کردیم. در آن مقاله، نشان دادیم در سیستم‌های پایستار، مجموع انرژی‌های پتانسیل و جنبشی ثابت می‌ماند. انرژی جنبشی، به شکلی از انرژی گفته می‌شود که وابسته به حرکت است. هر جسمی که حرکت می‌کند، انرژی جنبشی دارد. در طرف دیگر نیز هر جسمی که دارای انرژی جنبشی (Kinetic Energy) باشد، قطعاً در حال حرکت است. انرژی حرکتی، نام دیگریست که به این شکل از انرژی گفته می‌شود. انرژی جنبشی مفهوم ساده‌ای دارد و استخراج فرمول‌های آن نیز کار دشواری نیست.

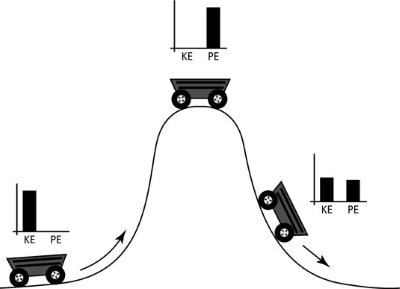
برای اینکه جسمی شتاب داشته باشد، باید به آن نیرو وارد کنیم. اعمال نیرو، مستلزم انجام کار است. پس از انجام کار، مقداری انرژی به جسم منتقل می‌شود و جسم با سرعت ثابت جدیدی به حرکت خود ادامه می‌دهد. انرژی منتقل شده در حین انجام این کار، انرژی جنبشی نامیده می‌شود. مقدار این انرژی، به جرم و سرعت مورد نظر بستگی دارد. انرژی جنبشی را می‌توان بین دو جسم مبادله یا به شکل‌های دیگر انرژی تبدیل کرد. به عنوان مثال، تصویر متحرک زیر را در نظر بگیرید. انرژی جنبشی هریک از آونگ‌ها به آونگ بعدی منتقل می‌شود تا آونگ آخر به حرکت دربیاید.

چگونگی محاسبه انرژی جنبشی

برای این که انرژی جنبشی را محاسبه کنیم، توضیحاتی را که پیش از این ارائه دادیم، دنبال می‌کنیم. فرض کنید مطابق شکل زیر، جسم $$\large m$$ روی سطحی قرار گرفته باشد. نیروی $$\large F$$ را موازی با سطح به جسم $$\large m$$ وارد می‌کنیم تا فاصله $$\large d$$ را طی کند. تعریف کار به صورت $$\large W=Fd\cos\theta$$ است ولی در اینجا، چون زاویه بین نیرو و مسیر حرکت $$\large \theta=0$$ بود، رابطه کار به شکل $$\large W=Fd$$ تبدیل می‌شود. از طرف دیگر، مطابق قانون دوم نیوتن، می‌دانیم $$\large F=ma$$ برقرار است. اکنون با یک جابجایی ساده، رابطه کار به شکل زیر تبدیل می‌شود.

$$\large W=mad$$

فیلم آموزش فیزیک پایه ۱ در فرادرس

کلیک کنید

اگر معادله سینماتیکی حرکت را به خاطر داشته باشید، می‌دانید که رابطه زیر بین سرعت و شتاب برقرار است.

$$\large V^2 \:-\: V_0^2 \:=\: 2ad$$

با ادغام دو رابطه اخیر، می‌توانیم رابطه کار را بازنویسی کنیم.

$$\large W\:=\: m.d.\: \frac {V^2 \:-\: V_0^2} {2d} \\~\\
\large \Rightarrow W\:=\: \frac {1} {2} m.V^2 \:-\: \frac {1} {2} m.V^2_0$$

از این رو، اگر کار خالصی روی یک جسم انجام شود، انرژی جنبشی‌اش به اندازه $$\large \frac {1} {2} m.V^2$$ تغییر می‌کند. بنا به قرارداد، اگر جسمی به جرم $$\large m$$ با سرعت $$\large V$$ در حال حرکت باشد، انرژی جنبشی آن برابر با $$\large \frac {1} {2} m.V^2$$ خواهد بود. از سوی دیگر هم می‌توان بیان کرد که تغییر انرژی جنبشی هر جسم برابر با کار خالص انجام شده روی آن است.

$$\large W_{net} \:=\: \Delta K$$

این نتیجه به عنوان قضیه کار و انرژی شناخته می‌شود و مفهومی بسیار کلی دارد. حتی اگر اندازه و جهت نیروها هم تغییر کند، باز هم این قضیه معتبر است.

هنگام مطالعه انرژی جنبشی، باید چند نکته را در نظر گرفت.

• انرژی جنبشی با مربع سرعت جسم متناسب است. به عبارت دیگر، اگر سرعت جسم دو برابر شود، انرژی جنبشی آن چهار برابر خواهد شد. انرژی جنبشی اتومبیلی که با سرعت ۶۰ کیلومتر در ساعت در حرکت است، نسبت به اتومبیلی که سرعتی برابر با ۳۰ کیلومتر در ساعت دارد، چهار برابر است. در نتیجه، در صورت تصادف، آسیبی که به اتومبیل سریع‌تر وارد می‌شود، چهار برابر دیگری است.
• در حالی که سرعت می‌تواند مثبت یا منفی باشد، مقدار انرژی جنبشی، با مربع سرعت هم‌علامت بوده و همیشه صفر یا مثبت است.
• انرژی جنبشی کمیت برداری نیست و برای آن، هیچ جهتی تعریف نمی‌شود.

مثال: محاسبه انرژی جنبشی لوکوموتیو

سؤال: در سال $$\large 1986$$ میلادی و در تگزاس آمریکا، یکی از کارمندان راه‌آهن به نام ویلیام کراش، در یک رویداد نمایشی دو لوکوموتیو بدون سرنشین را در دو انتهای ریلی به طول $$\large 6.4 km$$ قرار داد. لوکوموتیوها روشن شدند و به سرعت به سمت یکدیگر به حرکت درآمدند. $$\large 40000$$ نفر، شاهد تصادف این دو لوکوموتیو بودند. بویلر هر دو لوکوموتیو منفجر شد و تکه‌های جدا شده‌ای که در هوا معلق بود، به صدها نفر صدمه زد و چند نفر نیز کشته شدند. اگر وزن و شتاب هریک از این دو لوکوموتیو را $$\large 1.2\times 10^6N$$ و $$\large 0.26 m/s^2$$ فرض کنیم، انرژی جنبشی کل این سیستم را قبل از لحظه برخورد به دست آورید.

پاسخ: ابتدا فرض می‌کنیم هر دو لوکوموتیو با شتاب ثابت مسیر را پیمودند. به این ترتیب، سرعت لوکوموتیو‌ها قبل از لحظه برخورد به صورت زیر محاسبه می‌شود.

$$\large V^2 \:=\: V^2_0 \:+\: 2a(x\:- \:x_0) \\~\\
\large \begin{cases}V_0 \:=\:0 \\ x\:-\: x_0\:=\: 3.2\times 10^3m\end{cases} \\~\\
\large \Rightarrow ~~~ V^2\:=\: 0\:+\: 2(0.26 m/s^2) (3.2 \times 10^3m) \\~\\
\large \Rightarrow ~~~ V\:=\: 40.8 m/s$$

اکنون با داشتن جرم و سرعت هر لوکوموتیو، انرژی جنبشی آن به راحتی قابل محاسبه است.

$$\large m\:=\: \frac {1.2 \times 10^6 \:N} {9.8\: m/s^2} \:=\: 1.22 \times 10^5 \:kg \\~\\
\large K\:=\: 2(\frac {1} {2} mV^2) \:=\: (1.22 \times 10^5 \:kg) (40.8\: m/s)^2 \\~\\
\large K\:=\: 2.0 \times 10^8 \:J$$

این مقدار انرژی با انرژی حاصل از انفجار بمب، قابل مقایسه است. در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی مکانیک
• مجموعه آموزش‌های مهندسی مکانیک
• لختی دورانی چیست — به زبان ساده
• تکانه از صفر تا صد — بخش اول: اصول و مفاهیم
• تکانه از صفر تا صد — بخش دوم: تکانه زاویه‌ای