ثابت جهانی گازها — از صفر تا صد
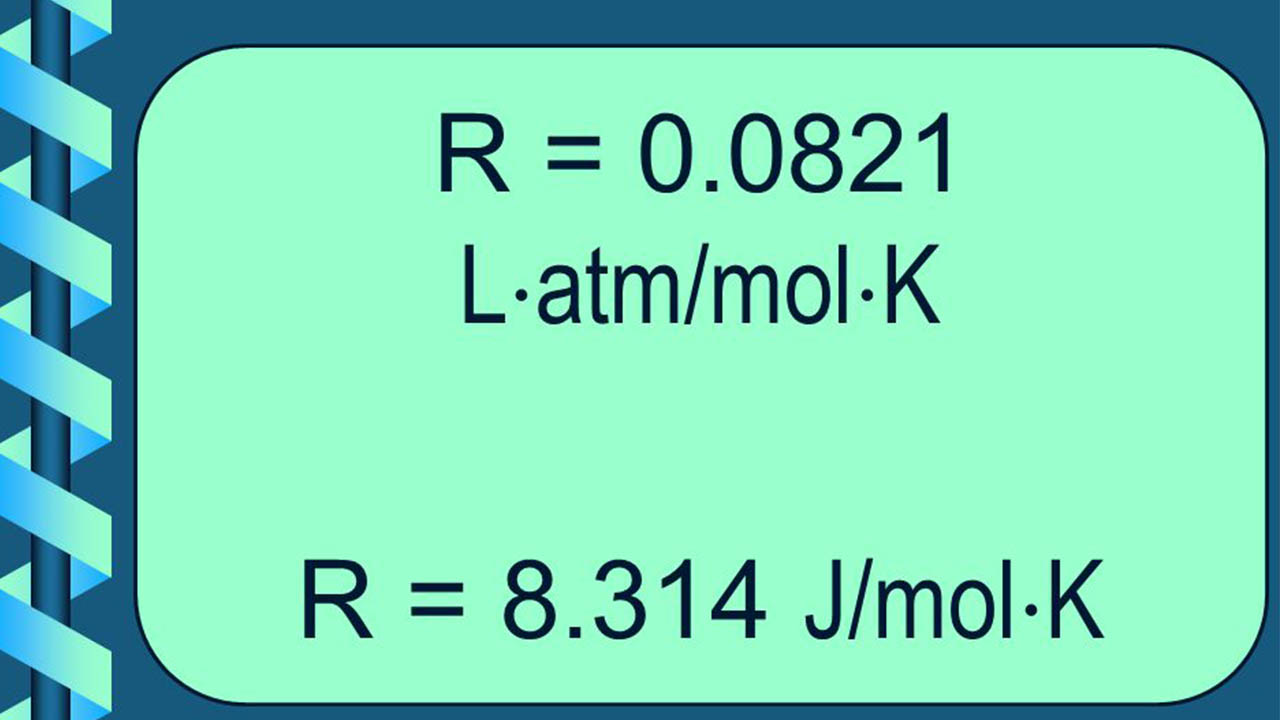
ثابت جهانی گازها که با نامهایی همچون ثابت مولی، ثابت گاز ایدهآل و ثابت گازها شناخته میشود را با نماد $$\overline{R}$$ نشان میدهند. ثابت جهانی گازها ترکیبی از ثابتها درقوانین بویل، شارل، آووگادرو و گیلوساک است. ثابت جهانی گازها نوعی ثابت فیزیکی به شمار میآید که در بسیاری از متون علمی شیمی و فیزیک و معادلات اساسی آن کاربرد دارد که از آنجمله میتوان به قانون گازهای ایدهآل و معادله نرنست اشاره کرد. از لحاظ فیزیکی، ثابت جهانی گازها یک ثابت تناسب است که مقیاسهای انرژی در فیزیک را به مقیاس دما مرتبط میکند.
تعریف ثابت جهانی گازها
ثابت جهانی گازها را به صورت حاصلضرب عدد آووگادرو $$(N_A)$$ در ثابت بولتزمن $$(k)$$ و به صورت زیر تعریف میکنند:
$${\displaystyle R = N _ {\rm { A }} k _ {}\,}$$
در سال 2019 و پس از تعریف مجدد واحدهای SI، مقدار عددی ثابت جهانی گازها به طور دقیق تعریف شد:
$$8.31446261815324 J ⋅ K − 1 ⋅mol − 1$$
علت نمادگذاری ثابت جهانی گازها با نماد $$R$$ مشخص نیست اما بسیاری پیشنهاد دادهاند که این ثابت، به پاس زحمات دانشمند فرانسوی، «آنری ویکترو رگنولت» (Henry Victor Regnault) به نام ثابت رگنولت نامگذاری شود چراکه از دادههای دقیق آزمایشگاهی او بمنظور محاسبه مقادیر اولیه ثابت جهانی گازها استفاده شده است.

ابعاد در ثابت جهانی گازها
در ادامه، ابعاد مورد استفاده در ثابت جهانی گازها را بررسی میکنیم. با استفاده از قانون گازهای ایدهآل، به عبارتی برای $$R$$ میرسیم:
$$P V = n R T$$
$$R = {\frac { P V }{ n T} }$$
در این رابطه، P فشار، V حجم، T دما و n، تعداد مول در یک ماده است. همانطور که میدانیم، تعریف فشار به صورت «نیرو» (Force) بر واحد «سطح» (Area) است. بنابراین، معادله گازها را میتوان به شکل زیر نوشت:
$${\displaystyle R = {\frac {{\dfrac {\mathrm { f orce } }{\mathrm {area} }}\times \mathrm {volume} }{\mathrm {amount} \times \mathrm {temperature} }}}$$
حجم و سطح نیز به صورت «طول مربع» $$((Lenght) ^ 2)$$ و «طول مکعب» $$((Lenght) ^ 3)$$ تعریف میشوند، بنابراین خواهیم داشت:
$${\displaystyle R = {\frac {{\dfrac {\mathrm {force} }{(\mathrm {length} ) ^ {2}}}\times (\mathrm {length} ) ^ { 3 }}{\mathrm {amount} \times \mathrm {temperature} }} = {\frac {\mathrm {force} \times \mathrm {length} }{\mathrm {amount} \times \mathrm {temperature} }}}$$
از آنجایی که حاصلضرب نیرو در طول، برابر با «کار» (Work) است، به رابطه زیر میرسیم:
$$R = {\frac {{\mathrm {work}}}{{\mathrm {amount}}\times {\mathrm {temperature}}}}$$
با بررسی رابطه بالا درمییابیم که مفهوم ثابت جهانی گازها برابر با کار بر دما بر مول است. این واحد را میتوان بر اساس واحدهای نشاندهنده کار یا انرژی همچون ژول بیان کرد. واحدهای دما، در مقیاس مطلق آنها (کلوین و رنکین) استفاده میشوند. علاوه بر این، نیرو را بر اساس قانون دوم نیوتون، میتوان به شکل زیر تعریف کرد:
$${\displaystyle \mathrm {force} = {\frac {\mathrm {mass} \times \mathrm {length} }{(\mathrm {time} ) ^ { 2 }}}}$$
در نتیجه، رابطه ثابت جهانی گازها به شکل زیر تبدیل میشود:
$${\displaystyle R = {\frac {\mathrm {mass} \times \mathrm {length} ^ {2}}{\mathrm {amount} \times \mathrm {temperature} \times (\mathrm {time} ) ^ { 2 }}}}$$
بنابراین، بر اساس واحدهای SI، مقدار عددی ثابت جهانی گازها به شکل زیر خواهد بود:
$$R = 8.314462618... kg⋅m^ 2 ⋅s^ { −2} ⋅ K^ { −1} ⋅ mol ^ { −1}$$

اندازهگیری ثابت جهانی گازها
در سال 2006، دقیقترین روش اندازهگیری ثابت جهانی گازها بوسیله اندازهگیری سرعت صوت $$c_a ( P , T )$$ در آرگون در دمای نقطه سهگانه آب بدست آمد.
به طوریکه مقادیر این سرعت را در فشارهای مختلف اندازهگیری کردند و به کمک برونیابی، به حد فشار صفر رساندند. در نهایت، رابطه زیر برای مقدار $$R$$ ارائه شد:
$${\displaystyle c _ {\mathrm {a} }(0 , T ) = { \sqrt {\frac {\gamma _ {0} R T } { A _ {\mathrm { r } }(\mathrm { A r } ) M _ {\mathrm {u} }}}}}$$
- $$γ_0$$: نسبت ظرفیت حرارتی است که برای گازهای تکاتمی همچون آرگون، برابر با $$\frac {5} {3}$$ است.
- $$T$$: دما بر حسب کلوین
- $$A_r (A r )$$: جرم اتمی نسبی آرگون
- $$M_u$$: برابر با $$10 ^ {− 3} kg⋅mol ^ {−1}$$
محاسبه ثابت جهانی گازها
همانطور که در مبحث گازهای واقعی بیان کردیم، تحت شرایط STP، یک مول از هر گازی، حجمی معادل 22/4 لیتر را اشغال میکند. با استفاده از این مقدار و مقادیر شرایط STP، مقدار عددی ثابت جهانی گازها به شکل زیر بدست خواهد آمد:
$$\begin{align} R & = \dfrac{ P V }{ n T } = \mathrm{\dfrac{1\: a t m\:\: 22.4\: L }{ 1 \: mol\:\: 273\: K }}\\ \\ & = \mathrm{0.08205\: \dfrac{L\: atm} {mol \cdot K}} \end{align}$$
زمانی که از واحدهای SI در محاسبه استفاده کنیم، اعداد و واحدها به صورت زیر تغییر پیدا میکنند:
$$\begin{align} R &= \mathrm{\dfrac {101325\: \dfrac{N} { m ^ 2 }\: 0.0224\: m ^ 3 } { 1\: mol\: 273\: K }}\\ \\ &= \mathrm{8.314\: \dfrac { J } { mol\cdot K }} \end{align}$$
همانطور که گفته شد، با توجه به اینکه انرژی را میتوان در واحدهای مختلفی بیان کرد، در نتیجه، ثابت جهانی گازها اعداد با واحدهای مختلفی را اختیار میکند که این مقادیر و واحدها در زیر آورده شدهاند:
$$\begin{align} R & = \mathrm{0.08205\: \dfrac{ L \: atm} {mol \cdot K }} &&\textrm{} \\ & = \mathrm{8.3145\: \dfrac { L \: k Pa} {mol \cdot K}} &&\mathrm{1 \: atm = 101.32\: k Pa } \\ &= \mathrm{ 8.3145 \: \dfrac{ J }{ mol \cdot K }} &&\mathrm{ 1\: J = 1\: L\: kPa} \\ &= \mathrm{1.987\: \dfrac{ cal }{ mol \cdot K }} &&\mathrm{ 1\: cal = 4.182\: J} \\ & = \mathrm{ 62.364\: \dfrac{ L\: torr}{mol \cdot K }} &&\mathrm{1\: atm = 760\: torr}\\ \end{align}$$
مثال
یک نمونه هوا که تنها شامل اکسیژن و نیتروژن است، در شرایط STP، چگالی برابر با $$1.3393 g / L$$ دارد. وزن و درصد مولی نیتروژن و اکسیژن را در نمونه پیدا کنید.
به کمک چگالی، جرم مولی متوسط را محاسبه میکنیم:
$$\begin{align} P M &= \rho R T\\ M &= 22.4 \times \rho\\ &= \mathrm{22.4\: L/mol \times 1.3393\: g/L}\\ &= \mathrm{30.0\: g / mol} \end{align}$$
فرض کنید که ۱ مول گاز داریم که $$x$$ مول آن نیتروژن و $$1-x$$ مول آن اکسیژن است. جرم مولی متوسط، حاصل متوسطگیری از مقدار مولها است. در نتیجه خواهیم داشت:
$$\mathrm{28.0\, x + 32.0 (1 - x) = 30.0}$$
$$\mathrm{- 4\, x = - 2}$$
با حل رابطه فوق درمییابیم که مقدار $$x$$ برابر با 0/5 میشود. در نتیجه، سهم اکسیژن و نیتروژن هرکدام برابر با نیم مول خواهد بود. حال برای پیدا کردن درصد جرمی، کافی است مقدار نیتروژن و اکسیژن را در یک مول (30 گرم) از این مخلوط پیدا کنیم:
$$\mathrm{ = 0.5 \times 28.0 = 14.0\: g}$$ جرم نیم مول نیتروژن
$$\mathrm{ = 0.5 \times 32.0 = 16.0\: g}$$ جرم نیم مول اکسیژن
$$\mathrm{ = 100 \times \dfrac{14.0}{30.0} = 46.7 \% }$$ درصد نیتروژن
$$\mathrm{ = 100 \times \dfrac{16.0}{30.0} = 100 - 46.7 = 53.3 \%}$$ درصد اکسیژن

ثابت ویژه گاز
ثابت ویژه گاز برای یک گاز یا مخلوطی از گازها $$(R_{ specific} ) $$ به صورت ثابت جهانی گازها تقسیم بر جرم مولی گاز یا مخلوط تعریف میشود:
$$R _ {{{\rm {specific}}}} = {\frac { R }{ M }}$$
این رابطه را میتوان به شکل ثابت بولتزمن تقسیم بر جرم مولی گاز نیز نشان داد:
$$R _ {{{\rm {specific}}}} = {\frac { R }{ M }}$$
رابطه دیگری که در این خصوص مطرح میشود، رابطه «مایر» (Mayer) است که ثابت ویژه گاز را به گرمای ویژه برای گاز کامل طبق رابطه زیر مرتبط میکند که در این رابطه، $$c_p$$، ظرفیت گرمایی ویژه در فشار ثابت و $$c_v$$، ظرفیت گرمایی ویژه در حجم ثابت است:
$$R _ {{{\rm {specific}}}} = c _ {{{\rm { p }}}} - c _ {{{\rm { v }}}}\ $$
به طور معمول، در متون مهندسی، ثابت ویژه گاز را با نماد $$R$$ نشان میدهند. در چنین مواردی، برای جلوگیری از گمراهی خواننده، ثابت جهانی گازها را با نماد $$\overline{R}$$ نشان میدهند.
اگر این مطلب برای شما مفید بوده است، آموزشها و مطالب زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس شیمی
- مجموعه آموزشهای مهندسی شیمی
- آموزش ترمودینامیک مهندسی شیمی
- فوگاسیته چیست؟ — به زبان ساده
- انرژی آزاد هلمهولتز — به زبان ساده
- جدول تناوبی — از صفر تا صد
^^










باسلام برای محاسبه ثابت عمومی گازها مقدار p چقدر باید لحاظ شود؟
با سلام؛
همانطور که در داخل متن نوشته شده است، برای محاسبه این ثابت باید از فشار یک atm کمک بگیرید.
با تشکر از همراهی شما با مجله فرادرس
سلام ، آیا در معادله گاز کامل میتوان از سلسیوس استفاده کرد و ثابت دیگری بجای R بکار برد؟
با سلام؛
همانطور که در داخل متن و در بخش اثبات آورده شده، در تمامی موارد از کلوین استفاده میشود و نمیتوان واحدهای دیگری را استفاده کرد.
با تشکر از همراهی شما با مجله فرادرس
سلام ، میخواستم بپرسم n.R.T همون انرژی درونی هم میشه؟؟؟؟؟
با سلام؛
برای آشنایی بیشتر با این موضوع بویژه انرژی درونی گاز ایدهآل پیشنهاد میکنیم مطلب «انرژی درونی — از صفر تا صد» را مطالعه کنید.
با تشکر از همراهی شما با مجله فرادرس