مخلوط گازها — به زبان ساده

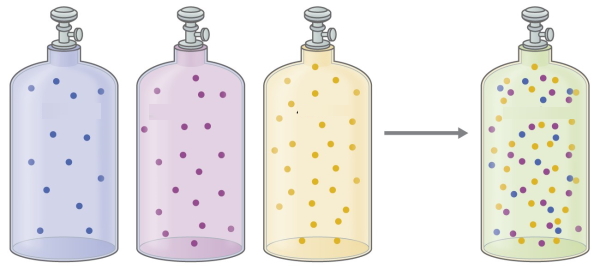
یکی از خواص گازها این است که میتوان آنها را با یکدیگر مخلوط کرد. با انجام این کار، یک مخلوط همگن خواهیم داشت. در این آموزش قصد داریم تا در خصوص مخلوط گازها یا مخلوطهای گازی صحبت کنیم. خوب است بدانید که در صورت داشتن ترکیب گازها در مخلوط، برخی از خواص مخلوط گازها به سادگی تعیین میشوند.
مقدمه
در مخلوط گازها، هر جزء از ترکیب را میتوان به طور جداگانه مورد بررسی قرار داد. هر جزء در مخلوط گازها حجم و دمای یکسان با سایر اجزا دارد چراکه گازها، بر اثر انبساط، ظرف حاوی خود را پر میکنند که این امر برای مخلوطهای گازی نیز یکسان است. البته هر گاز، فشار خود را دارد. در این خصوص، برای هر گاز، فشار جزئی تعریف میشود.
فشار جزئی در مخلوط گازها
فشار جزئی یک گاز که آنرا با نشان میدهند، فشاری است که یک گاز، در یک مخلوط گازی دارد. فشار جزئی را همچون سایر واحدهای فشار، با واحدهای «تور» (Torr)، میلیمتر جیوه یا اتمسفر نشان میدهند. زمانی که در خصوص گازهای خالص صحبت میکنیم، واژه فشار و زمانی که در خصوص مخلوط گازها صحبت میکنیم، واژه فشار جزئی را بکار میبریم.

قانون دالتون در فشارهای جزئی
قانون دالتون در فشارهای جزئی بیان میکند که فشار کلی یک مخلوط گازی، برابر با مجموع فشارهای جزئی هر جزء است.
با وجود اینکه این قانون، در ظاهر قانون سادهای به نظر میرسد اما دلیلی است بر اینکه گازها رفتاری مستقل از هم دارند. برای درک بهتر این موضوع، چند مثال را مطرح میکنیم.
مثال 1
مخلوطی از در فشار 2/33 اتمسفر و در فشار 0/77 اتمسفر در یک محفظه قرار دارند. فشار کل محفظه چقدر است؟
بر اساس قانون فشارهای جزئی دالتون، فشار کل برابر با مجموع فشارهای جزئی است. بنابراین به سادگی، با جمع این دو فشار، فشار کل محفظه بدست میآید:
مثال 2
یک محفظه ۲ لیتری حاوی در فشار 2/5 اتمسفر، به محفظه ۵ لیتری از گاز اکسیژن با فشار 1/9 اتمسفر متصل شده است. با اتصال این دو محفظه، هر دو گاز با یکدیگر مخلوط میشوند. فشار نهایی چقدر خواهد بود؟
با توجه به اینکه گازها رفتاری مستقل از یکدیگر دارند، فشار جزئی هرکدام را با استفاده از قانون بویل محاسبه کنیم و در نهایت، با جمع این دو فشار، به مقدار نهایی فشار در محفظه خواهیم رسید. در ابتدا از قانون بویل برای محسابه فشار جزئی گاز هیدروژن استفاده میکنیم:
با حل رابطه بالا برای خواهیم داشت:
بنابراین، فشار جزئی گاز هیدروژن برابر با 0/714 اتمسفر خواهد بود. حال، مانند روش قبل، فشار جزئی را برای گاز اکسیژن محاسبه میکنیم:
بر اساس قانون فشارهای جزئی دالتون، فشار کل، برابر با مجموع فشارهای جزئی است. در نتیجه، خواهیم داشت:

جمع آوری گاز
یکی از دلایی که از قانون فشارهای جزئی دالتون بهره میگیریم این است که گازها را به طور معمول از طریق حبابدهی به آب، جمعآوری میکنند. مایعات به طور پیوسته در حال تبخیر شدن هستند و این روند تا زمانی ادامه مییابد که بخار، به فشار جزئی ماده مورد نظر برسد. به این فشار جزئی، فشار بخار میگویند. توجه داشته باشید زمانی که یک ماده در شرایط مشخصی، به شکل گاز وجود داشته باشد، از واژه فشار جزئی استفاده میکنیم اما اگر مادهای در شرایط معمول، به صورت مایع باشد، واژه فشار بخار را برای بیان شکل گازی آن در نظر میگیریم.
هر زمانی که گازی بالای آب جمع شود، فشار کل برابر است با مجموع فشار جزئی گاز و فشار بخار آب. در نتیجه، مقدار گاز جمع شده، کمتر از مقدار متناظر با فشار کل خواهد بود. برای درک بهتر این موضوع، مثالی ارائه میکنیم.
مثال
گاز هیدروژن در اثر واکنش نیتریک اسید و آهن تولید میشود. برای جمع آوری این گاز، یک مخزن ۲ لیتری را به صورت وارونه در حوضچهای از آب با دمای ۲۲ درجه سانتیگراد قرار میدهیم. در انتهای فرآیند، فشار جزئی داخل مخزن، برابر با است. در این فرآیند، چه مقدار گاز هیدروژن تولید شده است؟ (فشار بخار آب در دمای 22 درجه سانتیگراد برابر با است.)
برای حل این سوال باید توجه داشته باشیم که فشار کل، شامل فشار بخار آب هم هست. بر اساس قانون فشارهای جزئی دالتون، فشار کل، برابر با مجموع فشارهای جزئی است. بنابراین، خواهیم داشت:
حال، از قانون گازهای ایدهآل کمک میگیریم تا تعداد مولها را محاسبه کنیم. در این خصوص فراموش نکنید که دما باید به کلوین تبدیل شود.
در رابطه بالا، تمامی واحدها به غیر از مول، حذف میشوند. بنابراین خواهیم داشت:
کسر مولی در مخلوط گازها
کسر مولی در محاسبات مخلوط گازها کاربرد بسیاری دارد و عبارتست از نسبت تعداد مولهای جزء i در مخلوط به تعداد کل مولهای آن:
تعداد کل مولها / تعداد مول جزء i
توجه داشته باشید که کسر مولی را به صورت درصد بیان نمیکنند و مقدار آن بین صفر تا 1 است. به طور مثال، ترکیب 4 گرم هلیوم و 5 گرم نئون را در نظر بگیرید. اگر هر دو را به مول تبدیل کنیم، خواهیم داشت:
مجموع هر دو ماده برابر با 1/25 مول خواهد بود. برای محاسبه کسر مولی هر جزء، به صورت زیر عمل میکنیم. رابطه زیر بیان میکند که مجموع کسرهای مولی برابر با ۱ خواهد بود:
راه دیگری نیز برای تعیین کسر مولی در مخلوط گازها وجود دارد. با توجه به اینکه در مخلوط گازها حجم و دمای یکسانی برای هر گاز داریم، تعداد مول گازها با فشار جزئی آنها متناسب است. بنابراین، کسر مولی در مخلوط گازها را میتوان به کمک نسبت فشارهای جزئی هم محاسبه کرد:
این رابطه به ما کمک میکند تا بدون محاسبه تعداد مولها، کسر مولی را محاسبه کنیم.
گازهای ایدهآل و فشار جزئی
زمانی که مخلوطی از دو گاز ایدهآل داشته باشیم، به کمک قانون گازهای ایدهآل و فشارهای جزئی دالتون، رابطه زیر را برای محاسبه فشار کل خواهیم داشت:
به همین شکل، رابطه کلی زیر را میتوان برای فشار کل در مخلوط گازها نوشت:
رابطه بالا بیان میکند که برای یک گاز ایدهآل، فشار گاز تنها به تعداد کل گازهای موجود بستگی دارد، خواه این گاز به صورت خالص باشد خواه به صورت مخلوطی از گازها مختلف.
مثال
غواصها به همراه خود باید به جای هوای فشرده، کپسولی شامل مخلوطی از گازها داشته باشند تا دچار بیماری ناشی از کاهش ناگهانی فشار (DSC) نشوند. در اعماق حدود 350 فوت، این غواصها در معرض فشاری برابر با 10 اتمسفر قرار دارند. سیلندری که به طور معمول این افراد همراه خود دارند شامل 51/2 گرم و 326/4 گرم هلیوم و حجم آن، برابر با 10 لیتر است. فشار جزئی هر گاز را در دمای 20 درجه سانتیگراد محاسبه کنید. در این دما، فشار کل در سیلندر، چه میزان خواهد بود؟
برای حل این سوال، ابتدا تعداد مولهای هلیوم و اکسیژن را محاسبه میکنیم و سپس به کمک قانون گازهای ایدهآل، فشارهای جزئی هر گاز را بدست میآوریم. در نهایت، برای محاسبه فشار کل، بر اساس قانون فشارهای جزئی دالتون، این فشارها را با هم جمع میکنیم.
حال با داشتن مقادیر مولها، فشارهای جزئی را محاسبه میکنیم:
در نهایت، فشار کل، برابر با مجموع فشارهای جزئی است:
گازهای ایدهآل و کسر مولی
رابطه مشابهی را نیز میتوان برای مرتبط ساختن کسر مولی با تعداد مول در مخلوط گازها به کمک قانون گازهای ایدهآل بیان کرد.
با بازآرایی رابطه بالا، به معادله زیر میرسیم:
توجه داشته باشید که کسر مولی را میتوان با نماد هم نشان داد. رابطه بالا بیان میکند که فشار جزئی هر گاز در مخلوط گازها برابر است با حاصلضرب کسر مولی گاز در فشار کل. این رابطه، تاییدی است بر فرض رفتار ایدهآل در گازها. در نتیجه، فشار گاز در یک مخلوط، تنها به درصد ذرات آن گاز در مخلوط بستگی دارد و مستقل از خواص فیزیکی و شیمیایی آن خواهد بود. اتمسفر زمین شامل 78 درصد گاز نیتروژن، 21 درصد اکسیژن، 0/9 درصد آرگون و همچنین سایر گازهای دیگر همچون دیاکسید کربن و بخار آب است. بنابراین، کسر مولی نیتروژن را میتوان برابر با 0/78 دانست و بر اساس رابطه بالا، فشار جزئی نیتروژن نیز با فرض فشار اتمسفری 760 میلیمتر جیوه، 0/78 اتمسفر خواهد بود (البته مقادیر آزمایشگاهی ممکن است مقادیر دیگری را نشان دهند). به همین شکل میتوان فشار جزئی سایر گازهای تنفسی انسان را محاسبه کنیم.

مثال
جدول زیر، فشارهای اندازهگیری شده دم و بازدم انسان را نشان میدهند. کسر مولی گازهای بازدم را محاسبه کنید.
| نام گاز | فشار هوای دم (میلیمتر جیوه) | فشار هوای بازدم (میلیمتر جیوه) |
| 597 | 568 | |
| 158 | 116 | |
| 0/3 | 28 | |
| 5 | 48 | |
| 8 | 8 | |
| 767 | 767 |
برای محاسبه کسر مولی از رابطه زیر بهره میگیریم:
به طور مثال، برای محاسبه کسر مولی دیاکسید کربن، به صورت زیر عمل میکنیم:
جدول زیر، مقادیر کسر مولی محاسبه شده در هوای بازدم را نشان میدهند:
| نام گاز | کسر مولی |
| 0/741 | |
| 0/151 | |
| 0/037 | |
| 0/063 | |
| 0/010 |
غلظت گازها
راههای مختلفی برای بیان غلظت گازها جدا از فشار جزئی وجود دارد. این نوع غلظتها را به طور معمول از طریق نسبت ذرات، مولها، درصد مولی و کسر مولی بیان میکنند. برای غلظتهای بسیار کم، از واحدهایی همچون، غلظت در میلیون و غلظت در میلیارد استفاده میکنیم. توجه داشته باشید که ppm و ppb در مخلوط گازها به شکل دیگری و متفاوت با مایعات تعریف میشوند. برای یک مخلوط گازی، ppm برابر با تعداد ذرات (اتم، مولکول یا مول) یک جزء خاص در مخلوط، به ازای یک میلیون ذره در کل مخلوط است.
جمعبندی
در این آموزش، مطالبی را در خصوص مخلوط گازها بیان کردیم. فهمیدیم که فشار جزئی هر گاز در یک مخلوط، با کسر مولی آن تناسب دارد. همچنین، گفته شد که فشار اعمال شده هر گاز در یک مخلوط گازی، مستقل از فشار سایر گازهای موجود در مخلوط است. در نتیجه، فشار کل در یک مخلوط، برابر با مجموع فشارهای جزئی هر یک از اجزای مخلوط خواهد بود که این مفهوم را از طریق قانون فشارهای جزئی دالتون بیان کردیم. علاوه بر این، یاد گرفتیم که مقدار گاز موجود در یک مخلوط گازی را میتوان به شکل کسر مولی یا فشار جزئی بیان کرد. اما کسر مولی هر جزء در یک مخلوط عبارتست از نسبت تعداد مولهای آن جزء به کل مولهای مخلوط گازی. در نهایت، بیان کردیم که در مخلوط گازها، فشار جزئی هر گاز برابر با حاصلضرب فشار کل در کسر مولی آن گاز است.
اگر این مطلب برای شما مفید بوده است، آموزشها و مطالب زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس شیمی
- مجموعه آموزشهای مهندسی شیمی
- آموزش موازنه انرژی و مواد
- قانون شارل — به زبان ساده
- گاز واقعی (حقیقی) — از صفر تا صد
- جدول تناوبی — از صفر تا صد
^^











سلام
من یک سیلندر گاز ۱۰ لیتری که شامل co با غلظت ۰.۳Mol% با گاز بالانس N2 هست موجود دارم. فشار سیلندر ۱۵۰ بار میباشد.
میخام بدونم با چه فرمولی میشه این غلظت رو تبدیل به ppm کرد.
یعنی co چند ppm میباشد.
تشکر
سوال دارم برای جداسازی یک مخلوط دوجزئی گازی و یک مخلوط دو جزئی مایع چه راهکاری پیشنهاد می دهید ؟
استاد بحرکاظمی حتما جوابش بهم بدین سپاسگزارم از لطف تون
با سلام؛
برای آشنایی با روشهای جداسازی، مطالعه مطالب زیر را پیشنهاد میکنیم:
روشهای جداسازی مواد در شیمی — از صفر تا صد
فیلتراسیون در شیمی — از صفر تا صد
مخلوط گازها — به زبان ساده
با تشکر از همراهی شما با مجله فرادرس
نمیشه یکم ساده تر توضیح بدین حالا ماکه فهمیدیم بقیه چیکار کنن والا هنوز نخوندم دارم نظر میدم ?
سلام سوال بنده اینه <<<< ما ۱۰ عدد کپسول هوای ۲۰۰ بار با حجم 22 لیتر داریم و میخواهیم با اون یک کپسول ثانویه را به اندازه ۱۸۰ بار هوا که حجمش 43 لیتر است پر کنیم . حالا سوال اینه که با چند تا از کپسول های ۲۰۰ بار 22 لیتری میتوانیم این کپسول را به اندازه ۱۸۰ بار پر کنیم؟ فرمول نحوه محاسبه ریاضی آن را میخاستم و سوال دیگه اینکه هوای باقی مانده در هر کدان از 10 کپسولی که استفاده شده چقدر است؟؟فرمول نحوه محاسبه ریاضی
با سلام
ممنون میشوم در ارتباط با حل مسله ریز راهنمایی فرمایید.
دو ظرف داریم یکی حاوی گاز آرگون و دیگری حاوی مخلوط آرگون (85%) و دی اکسید کربن (15%) است. اگر از خروجی این ظروف به اندازه مساوی ( flow rate یکسان) گاز ها را به ظرف دیگری منتقل کنیم ترکیب نهایی مخلوط حاوی چند درصد آرگون و چند درصد دی اکسید کربن خواهد بود؟
اگر flow rate متغیر باشد چطور؟
دما و فشار اولیه برای هر دو ظرف یکسان است.
پیشاپیش از پاسخ شما سپاسگزارم
ارادتمند شما
با سلام
(راجع به مقاله مخلوط گازه -به زبان ساده نوشته:جناب مهندس سهیل بحر کاظمی)
ضمن تشکر از زحمتی که کشیده اید و متن بسیار خوبی که تهیه فرموده اید، خواهش میکنم اگر امکان داشته باشد یک مروری مجدد روی متن خوبتان بنمایید و برخی غلطهای تایپی را تصحیح نمایید، مطلب عالی شما بسیار عالی تر هم خواهد شد.
بعنوان نمونه در مثال مربوط به جمع آوری گاز هیدروژن در اثر واکنش نیتریک اسید و آهن، پس از حل رابطه بجای فشار هیدروژن مساوی 713تور نوشته شده فشار آب برابر 713تور.
اگرخواننده این مطلب دانش آموز باشد ممکن است گیج شده واصلاً از ادامه کل مطلب خودداری کند.
باتشکر مجدد از موضوع ارایه شده عالی شما
با سلام؛
از ارائه بازخورد شما بسیار سپاسگزاریم. متن مورد نظر بازبینی و اصلاح شد.
با تشکر