انبساط چیست؟ — با مثال و به زبان ساده

در این مطلب در مورد انبساط و ویژگی‌های آن صحبت می‌کنیم و انبساط خطی، سطحی و حجمی را توضیح می‌دهیم. همچنین تاثیر انبساط را بر پارامترهای دیگر جسم بررسی و تحلیل می‌کنیم. خواندن این مطلب برای دانش آموزان پایه پنجم و هفتم و والدین آن‌ها مفید خواهد بود.

انبساط چیست؟

انبساط حرارتی تمایل ماده به تغییر شکل، مساحت، حجم و چگالی خود در پاسخ به تغییر دما است که معمولاً شامل انتقال فاز نمی‌شود. دما تابع یکنواخت میانگین انرژی جنبشی مولکولی یک ماده است. هنگامی که یک ماده گرم می‌شود، مولکول‌ها شروع به ارتعاش و حرکت بیشتر می‌کنند و معمولاً فاصله بیشتری بین خود ایجاد می‌کنند. موادی که با افزایش دما منقبض می‌شوند غیرعادی هستند و فقط در محدوده دمایی محدودی رخ می‌دهند.

انبساط نسبی که تنش نیز نامیده می‌شود، تقسیم بر تغییر دما را ضریب انبساط حرارتی خطی ماده می‌گویند و به طور کلی با دما تغییر می‌کند. با افزایش انرژی در ذرات، آن‌ها شروع به حرکت سریعتر و سریعتر می‌کنند و نیروهای بین مولکولی بین آن‌ها را تضعیف می‌کنند و در نتیجه ماده را منبسط می‌کنند.

پیش بینی انبساط چگونه صورت می‌گیرد؟

اگر معادله حالت یک جسم در دسترس باشد، می‌توان از آن برای پیش بینی مقدار انبساط حرارتی در تمام دماها و فشارهای مورد نیاز، همراه با بسیاری از توابع حالت دیگر استفاده کرد.

انبساط حرارتی منفی چیست؟

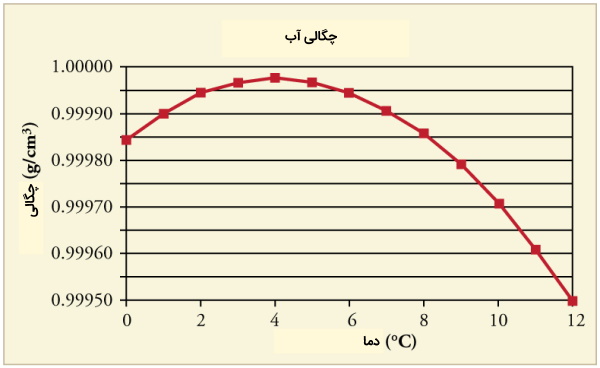
تعدادی از مواد در اثر گرم کردن در محدوده دمایی خاص منقبض می‌شوند. این حالت معمولاً به جای انقباض حرارتی انبساط حرارتی منفی نامیده می‌شود. به عنوان مثال، ضریب انبساط حرارتی آب با سرد شدن تا 3٫983 درجه سانتی گراد به صفر می‌رسد و سپس در زیر این دما منفی می‌شود.

این موضوع بدان معنا است که آب در این دما دارای حداکثر چگالی است و این باعث می شود که توده‌های آبی این دما را در اعماق پایین خود در دوره‌های طولانی هوای زیر صفر حفظ کنند. همچنین، سیلیکون نسبتاً خالص دارای ضریب انبساط حرارتی منفی برای دماهای بین 18 تا 120 کلوین است.

عوامل موثر بر انبساط چیست؟

برخلاف گازها یا مایعات، مواد جامد تمایل دارند شکل خود را هنگام انبساط حرارتی حفظ کنند. انبساط حرارتی عموماً با افزایش انرژی پیوند کاهش می‌یابد که بر نقطه ذوب جامدات نیز تأثیر می‌گذارد. بنابراین، مواد با نقطه ذوب بالا به احتمال زیاد انبساط حرارتی کمتری دارند. به طور کلی، مایعات کمی بیشتر از جامدات منبسط می‌شوند. انبساط حرارتی شیشه‌ها در مقایسه با کریستال‌ها کمی بیشتر است.

در دمای انتقال شیشه‌ای، باز آرایی‌هایی که در یک ماده بی شکل رخ می‌دهد منجر به ناپیوستگی مشخصه ضریب انبساط حرارتی و گرمای ویژه می‌شود. این ناپیوستگی‌ها امکان تشخیص دمای انتقال شیشه‌ای را فراهم می‌کند که در آن مایع فوق خنک شده به شیشه تبدیل می‌شود. یک اثر جالب «سرد شدن با گرم کردن» زمانی رخ می‌دهد که یک مایع شیشه‌ساز از بیرون گرم می‌شود و منجر به افت دما در عمق مایع می‌شود.

جذب یا دفع آب یا حلال‌های دیگر می‌تواند اندازه بسیاری از مواد ارگانیک را تغییر دهد. بسیاری از مواد آلی بیشتر به دلیل این اثر تغییر اندازه می‌دهند تا به دلیل انبساط حرارتی. پلاستیک‌های معمولی که در معرض آب قرار می‌گیرند، در درازمدت می‌توانند درصد زیادی منبسط شوند.

تاثیر انبساط بر چگالی چگونه است؟

انبساط حرارتی فضای بین ذرات یک ماده را تغییر می‌دهد، که در نتیجه حجم ماده تغییر می‌کند در حالی که جرم آن به میزان ناچیزی تغییر پیدا خواهد کرد (این مقدار ناچیز از معادله انرژی-جرم حاصل می‌شود)، در نتیجه چگالی آن را تغییر می‌دهد، که بر هر نیروی شناوری تأثیرگذار است. این موضوع نقش مهمی در جابجایی توده‌های سیال گرم شده غیریکنواخت ایفا می‌کند، به ویژه که انبساط حرارتی را تا حدی مسئول جریان‌های باد و اقیانوس می‌کند.

ضرایب در انبساط حرارتی

ضریب انبساط حرارتی توضیح می‌دهد که چگونه اندازه یک جسم با تغییر دما تغییر می‌کند. این کمیت به طور خاص، تغییر کسری در اندازه را به ازای هر درجه تغییر دما در یک فشار ثابت اندازه‌گیری می‌کند، به طوری که ضرایب پایین‌تر تمایل کمتر برای تغییر اندازه را توصیف می‌کنند. انواع مختلفی از ضرایب انبساط حرارتی وجود دارد که شامل ضریب انبساط حجمی، ضریب انبساط سطحی و ضریب انبساط خطی هستند. انتخاب ضریب بستگی به کاربرد خاص آن و اینکه کدام ابعاد مهم در نظر گرفته می‌شوند، دارد. به عنوان مثال برای جامدات، ممکن است فقط به تغییر در طول یا در یک منطقه مشخص توجه داشته باشیم.

ضریب انبساط حرارتی ابتدایی ترین ضریب انبساط و مرتبط‌ترین آن برای سیالات است. به طور کلی، مواد با تغییر دمای آن‌ها منبسط یا منقبض می‌شوند و انبساط یا انقباض در همه جهات رخ می‌دهد. به موادی که در هر جهت با سرعت یکسانی منبسط می‌شوند، همسانگرد می‌گویند. برای مواد همسانگرد، مساحت و ضریب انبساط حرارتی حجمی به ترتیب تقریباً دو برابر و سه برابر بزرگتر از ضریب انبساط حرارتی خطی است. تعاریف ریاضی این ضرایب در زیر برای جامدات، مایعات و گازها آورده شده است.

ضریب انبساط حرارتی به صورت کلی

در حالت کلی ضریب انبساط حرارتی گاز، مایع یا جامد برابر است با:

$${\displaystyle \alpha =\alpha _{\text{V}}={\frac {1}{V}}\,\left({\frac {\partial V}{\partial T}}\right)_ {p}}$$

زیرنویس $$p$$ برای مشتق نشان می‌دهد که فشار در طول انبساط ثابت نگه داشته می‌شود و زیرنویس V تاکید می‌کند که انبساط حجمی است و وارد این تعریف کلی می‌شود. در مورد گاز، ثابت نگهداشتن فشار مهم است زیرا حجم گاز به میزان قابل توجهی با فشار و همچنین دما تغییر می‌کند. برای گازی با چگالی کم این را می‌توان از گاز ایده آل مشاهده کرد

انبساط در جامدات چگونه است؟

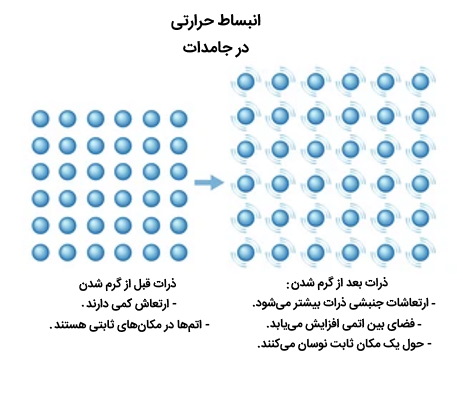
هنگام محاسبه انبساط حرارتی باید در نظر گرفت که آیا جسم آزاد است یا محدود است. اگر جسم آزاد باشد و منبسط شود، انبساط یا تنش ناشی از افزایش دما را می‌توان به سادگی با استفاده از ضریب انبساط حرارتی محاسبه کرد. اگر جسم به گونه‌ای محدود شود که نتواند منبسط شود، آن گاه تنش درونی با تغییر دما ایجاد می‌شود یا تغییر می‌کند. این تنش را می‌توان با در نظر گرفتن کششی که در صورت آزاد بودن جسم برای انبساط رخ می‌دهد و تنش لازم برای کاهش آن کشش به صفر، از طریق رابطه تنش/کشش که با مدول الاستیک یا یانگ مشخص می‌شود، محاسبه کرد.

در مورد خاص مواد جامد، فشار محیط خارجی معمولاً بر اندازه یک جسم تأثیر محسوسی ندارد و بنابراین معمولاً نیازی به در نظر گرفتن تأثیر تغییرات فشار نیست. در مهندسی جامدات، معمولاً ضرایب انبساط حرارتی به طور قابل توجهی در محدوده دماهایی که برای استفاده طراحی شده‌اند تغییر نمی‌کنند، بنابراین در مواردی که دقت بسیار بالایی لازم نیست، محاسبات عملی را می‌توان بر اساس یک مقدار ثابت و متوسط ​​از ضریب انبساط انجام داد.

انبساط خطی در جامدات چگونه است؟

انبساط خطی به معنای تغییر در یک بعد (طول) در مقابل تغییر حجم (انبساط حجمی) است. برای اولین تقریب، تغییر در اندازه گیری طول یک جسم به دلیل انبساط حرارتی به تغییر دما توسط ضریب انبساط حرارتی خطی (CLTE) مرتبط است. این تغییر کسری طول به ازای درجه تغییر دما است. با فرض اینکه تاثیر فشار ناچیز است، می‌توانیم بنویسیم:

$$\alpha_{L}=\frac{1}{L}\frac{dL}{dT}$$

که در معادله بالا $${\displaystyle L}$$ اندازه‌ طول ویژه است و $${\displaystyle \mathrm {d} L/\mathrm {d} T}$$ نرخ تغییر بُعد خطی در واحد تغییر دما است. تغییر در بُعد خطی را می‌توان به صورت زیر تخمین زد:

$$\frac{\Delta L}{L}=\alpha_{L} \Delta T$$

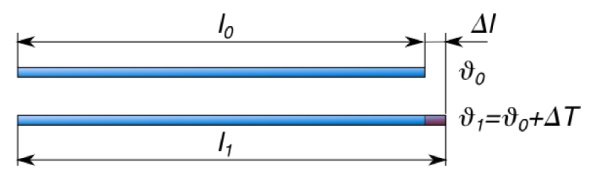
این تخمین تا زمانی که ضریب انبساط خطی تغییر چندانی در تغییر درجه حرارت یعنی $${\displaystyle \Delta T}$$ نداشته باشد خوب عمل می‌کند و در این حالت تغییر طول یعنی $${\displaystyle \Delta L/L\ll 1}$$ کوچک است. اگر هر یک از این شرایط برقرار نباشد، معادله دیفرانسیل دقیق (با استفاده از $${\displaystyle \mathrm {d} L/\mathrm {d} T}$$) باید توسط انتگرال محاسبه شود.

اثرات بر کشش در جامدات چگونه است؟

برای مواد جامد با طول قابل توجه، مانند میله‌ها یا کابل‌ها، تخمینی از میزان انبساط حرارتی را می‌توان با کشش ماده توصیف کرد که توسط $${\displaystyle \epsilon _{\mathrm {thermal} }}$$ و به این صورت تعریف می‌شود:

$${\displaystyle \epsilon _{\mathrm {thermal} }={\frac {(L_{\mathrm {final} }-L_{\mathrm {initial} })}{L_{\mathrm {initial} }}}}$$

که در آن $${\displaystyle L_{\mathrm {initial} }}$$ طول جسم قبل از تغییر دما و $${\displaystyle L_{\mathrm {final} }}$$ طول بعد از تغییر دما است. برای بیشتر جامدات، انبساط حرارتی متناسب با تغییر دما است و داریم:

$${\displaystyle \epsilon _{\mathrm {thermal} }\propto \Delta T}$$

بنابراین، تغییر در کشش یا دما را می‌توان با موارد زیر تخمین زد:

$${\displaystyle \epsilon _{\mathrm {thermal} }=\alpha _{L}\Delta T}$$

که

$${\displaystyle \Delta T=(T_{\mathrm {final} }-T_{\mathrm {initial} })}$$

تفاوت دمای بین دو سر جسم که بر حسب درجه فارنهایت، درجه رانکین، درجه سانتیگراد یا کلوین اندازه گیری می شود و $${\displaystyle \alpha _{L}}$$ ضریب خطی انبساط حرارتی بر حسب یک بر روی درجه فارنهایت، یک بر روی رانکین، یک بر روی درجه سانتیگراد یا یک بر روی کلوین است که به ترتیب با $$^{\circ}F^{-1}, R^{-1}, ^{\circ}C^{-1}$$ یا $$K^{-1}$$ نشان داده می‌شوند. در زمینه مکانیک پیوسته، انبساط حرارتی و اثرات آن به عنوان کشش ویژه و تنش ویژه در نظر گرفته می‌شوند.

انبساط سطحی در جامدات چگونه است؟

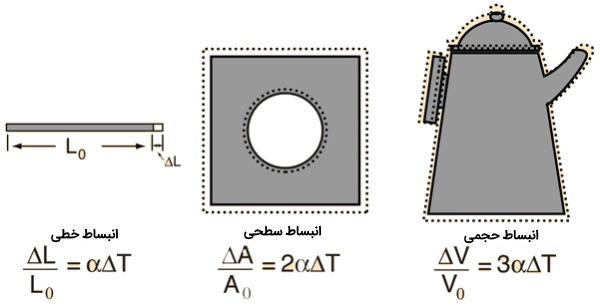
ضریب انبساط حرارتی سطح، تغییر در ابعاد سطح یک ماده را به تغییر دما مرتبط می‌کند. این تغییر کسری در سطح به ازای درجه تغییر دما است. با فرض اینکه تغییرات فشار ناچیز است، داریم:

$${\displaystyle \alpha _{A}={\frac {1}{A}}\,{\frac {\mathrm {d} A}{\mathrm {d} T}}}$$

که در آن $$A$$ مساحت ناحیه مورد نظر روی جسم است و $$\frac{dA}{dT}$$ نرخ تغییر آن ناحیه در واحد تغییر دما است. تغییر در سطح را می‌توان به صورت زیر تخمین زد:

$${\displaystyle {\frac {\Delta A}{A}}=\alpha _{A}\Delta T}$$

این معادله تا زمانی که ضریب انبساط سطح نسبت به تغییرات دما یعنی $$\Delta T$$ تغییر چندانی نداشته باشد و تغییرات در اندازه مساحت یعنی $${\displaystyle \Delta A/A\ll 1}$$ کوچک باشد به خوبی شرایط را توضیح می‌دهد. اگر یکی از این شرایط برقرار نباشد، باید از معادله انتگرال گرفت.

انبساط حجمی در جامدات چگونه است؟

برای یک جامد، می‌توانیم اثرات فشار روی ماده را نادیده بگیریم و ضریب انبساط حرارتی حجمی (یا مکعبی) را می‌توان به صورت زیر نوشت:

$${\displaystyle \alpha _{V}={\frac {1}{V}}\,{\frac {\mathrm {d} V}{\mathrm {d} T}}}$$

که در آن V حجم ماده و $${\frac {\mathrm {d} V}{\mathrm {d} T}}$$ سرعت تغییرات حجم با دما است. این بدین معنی است که حجم یک ماده به مقدار کسری ثابت تغییر می‌کند. به عنوان مثال، یک بلوک فولادی با حجم 1 متر مکعب ممکن است زمانی که دما 50 کلوین افزایش یابد تا 1٫002 متر مکعب منبسط شود، این انبساط $$0.2\ %$$ است. اگر یک بلوک فولادی با حجم 2 متر مکعب داشتیم، در همان شرایط به 2٫004 متر مکعب افزایش می‌یافت که باز هم 0٫2 درصد افزایش می‌یابد. ضریب انبساط حجمی برای دمای ۵۰ درجه کلوین $$0.2\%$$ یا $$0.004\%$$ یک بر روی درجه کلوین خواهد بود. بدین ترتیب اگر از قبل ضریب انبساط را بدانیم، می‌توانیم تغییر حجم را محاسبه کنیم و داریم:

$${\displaystyle {\frac {\Delta V}{V}}=\alpha _{V}\Delta T}$$

که در آن $${\displaystyle \Delta V/V}$$ تغییر کسری در حجم (مثلاً 0٫002) و $${\displaystyle \Delta T}$$ تغییر دما (50 درجه سانتیگراد) است. مثال بالا فرض می‌کند که ضریب انبساط با تغییر دما تغییر نکرده و افزایش حجم در مقایسه با حجم اولیه کم است. این موضوع همیشه درست نیست، اما برای تغییرات کوچک دما، تقریب خوبی است. اگر ضریب انبساط حجمی به میزان قابل توجهی با دما تغییر کند یا افزایش حجم قابل توجه باشد، معادله فوق به شکل زیر نوشته می‌شود:

$$\begin{aligned}
&\ln \left(\frac{V+\Delta V}{V}\right)=\int_{T_{i}}^{T_{f}} \alpha_{V}(T) \mathrm{d} T \\
&\frac{\Delta V}{V}=\exp \left(\int_{T_{i}}^{T_{f}} \alpha_{V}(T) \mathrm{d} T\right)-1
\end{aligned}$$

که $$\alpha_{V}(T)$$ ضریب انبساط حجمی به عنوان تابعی از دما یعنی $$T$$ است و همچنین $$T_i$$ و $$T_f$$ به ترتیب دمای اولیه و نهایی هستند.

مواد ایزوتروپیک یا همسانگرد در انبساط چگونه رفتار می‌کنند؟

برای مواد همسانگرد یا ایزوتروپیک ضریب انبساط حرارتی حجمی سه برابر ضریب انبساط حرارتی خطی است و داریم:

$$\alpha_V=3\alpha_L$$

این نسبت به این دلیل به وجود می آید که حجم از سه جهت متعامد متقابل تشکیل شده است. بنابراین، در یک ماده همسانگرد برای تغییرات دیفرانسیل کوچک، یک سوم انبساط حجمی مقدار آن در یک راستا یا محور است. به عنوان مثال، مکعبی از فولاد را در نظر بگیرید که اضلاع آن به طول L است. حجم اصلی $$V=L^3$$ خواهد بود و حجم جدید، پس از افزایش دما برابر است با:

$$V+\Delta V=(L+\Delta L)^{3}=L^{3}+3 L^{2} \Delta L+3 L \Delta L^{2}+\Delta L^{3}\\ \approx L^{3}+3 L^{2} \Delta L=V+3 V \frac{\Delta L}{L}$$

ما به راحتی می‌توانیم جملاتی که در آن مجذور تغییرات طول وجود دارد را نادیده بگیریم زیرا مقدار آن‌ها بسیار کوچک است، در نتیجه داریم:

$${\displaystyle {\frac {\Delta V}{V}}=3{\Delta L \over L}=3\alpha _{L}\Delta T}$$

تقریب بالا برای تغییرات دما و ابعاد کوچک صادق است (یعنی زمانی که $${\displaystyle \Delta T}$$
و $${\displaystyle \Delta L}$$ کوچک هستند). اما اگر بخواهیم با استفاده از مقادیر بزرگ $${\displaystyle \Delta T}$$ این رابطه را برقرار کنیم، این نسبت باقی نمی‌ماند. در این حالت‌ها، جمله سوم و گاهی اوقات حتی جمله چهارم در عبارت فوق باید در نظر گرفته شود. به طور مشابه، ضریب انبساط حرارتی سطح دو برابر ضریب خطی است و داریم:

$${\displaystyle \alpha _{A}=2\alpha _{L}}$$

این نسبت را می‌توان به روشی مشابه با مثال خطی بالا و با توجه به اینکه مساحت یک سطح روی مکعب برابر با $$L^2$$ است، یافت. همچنین در ضریب انبساط سطحی نیز در هنگام مواجهه با مقادیر بزرگ $$\Delta T$$ باید ملاحظات یکسانی در نظر گرفته شود. به بیان ساده تر، اگر طول یک جامد از 1 متر به 1٫01 متر منبسط شود، مساحت از 1 متر مربع به 1٫0201 متر مربع و حجم از 1 متر مکعب به 1٫030301 متر مکعب افزایش می‌یابد.

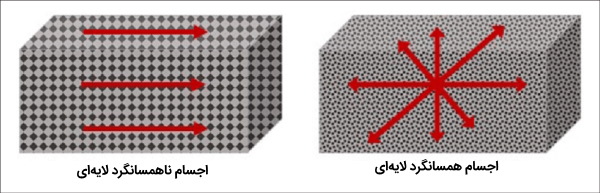
مواد ناهمسانگرد در انبساط چگونه رفتار می‌کنند؟

مواد با ساختارهای ناهمسانگرد، مانند کریستال‌ها (با تقارن کمتر از مکعب، برای مثال فازهای مارتنزیتی) و بسیاری از کامپوزیت‌ها، عموماً دارای ضرایب انبساط خطی متفاوتی در جهات مختلف هستند. در نتیجه، انبساط حجمی کل به طور نابرابر بین سه محور توزیع می‌شود. اگر تقارن کریستالی مونوکلینیک یا تری کلینیک باشد، حتی زوایای بین این محورها نیز در معرض تغییرات حرارتی هستند.

در چنین مواردی لازم است ضریب انبساط حرارتی را به عنوان یک تانسور با حداکثر شش عنصر مستقل در نظر گرفت. یک راه خوب برای تعیین عناصر تانسور، مطالعه انبساط توسط پراش پرتو ایکس است. تانسور ضریب انبساط حرارتی برای موادی که دارای تقارن مکعبی هستند (به عنوان مثال FCC، BCC) همسانگرد است.

انبساط هم فشار در گازهای ایده آل چگونه است؟

از آنجایی که گازها کل ظرفی را که اشغال می‌کنند پر خواهند کرد، فقط ضریب انبساط حرارتی حجمی در فشار ثابت، $${\displaystyle \alpha _{V}}$$ مورد توجه است. برای یک گاز ایده آل، می‌توان به راحتی رابطه $${\displaystyle pV_{m}=RT}$$ را با دیفرانسیل قانون گاز ایده آل به دست آورد. این معادله منجر به رابطه زیر می‌شود و داریم:

$${\displaystyle p\mathrm {d} V_{m}+V_{m}\mathrm {d} p=R\mathrm {d} T}$$

در معادله بالا $$p$$ فشار، $$V_{m}$$ حجم مولی و برابر با $${\displaystyle V_{m}=V/n}$$ است که n تعداد کل مول‌های گاز است، T دمای مطلق و R برابر با ثابت گاز است. برای یک انبساط حرارتی هم فشار $${\displaystyle \mathrm {d} p=0}$$ است به طوری که $${\displaystyle p\ \mathrm {d} V_{m}=R\ {d} T}$$ است و ضریب انبساط حرارتی هم فشار برابر است با:

$${\displaystyle \alpha _{V}\equiv {\frac {1}{V}}\left({\frac {\partial V}{\partial T}}\right)_{p}={\frac { 1}{V_{m}}}\left({\frac {\partial V_{m}}{\partial T}}\right)_{p}={\frac {1}{V_{m}}} \left({\frac {R}{p}}\right)={\frac {R}{pV_{m}}}={\frac {1}{T}}}$$

که تابعی از دما است و بدین ترتیب دو برابر شدن دما ضریب انبساط حرارتی را به نصف کاهش می‌دهد.

انبساط در مایعات چگونه است؟

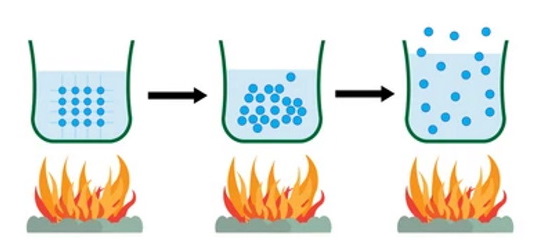
انبساط حرارتی مایعات معمولاً بیشتر از جامدات است زیرا نیروهای بین مولکولی موجود در مایعات نسبتاً ضعیف هستند و مولکول‌های تشکیل دهنده آن حرکت بیشتری دارند. از نظر تئوری، ضریب انبساط خطی را می‌توان از ضریب انبساط حجمی ($$\alpha_V \approx 3\alpha_L$$) یافت. مایعات برخلاف جامدات شکل مشخصی ندارند و شکل ظرف را به خود می‌گیرند و در نتیجه، مایعات طول و مساحت مشخصی ندارند. بنابراین انبساط خطی و سطحی مایعات اهمیتی ندارد. با این حال، $$\alpha_L$$ گاهی اوقات از مقدار تجربی $$\alpha_V$$ محاسبه می‌شود.

مایعات به طور کلی در گرما انبساط می‌یابند. با این حال، آب یک استثنا برای این رفتار کلی است. آب در دمای زیر 4 درجه سانتیگراد در اثر گرما منقبض می‌شود که منجر به ضریب انبساط حرارتی منفی می‌شود. در دماهای بالاتر، آب رفتار معمولی‌تری با ضریب انبساط حرارتی مثبت نشان می دهد. انبساط حرارتی جامدات معمولاً وابستگی کمی به دما به جز در دماهای پایین نشان می‌دهد، در حالی که مایعات می‌توانند با سرعت‌های مختلف در دماهای مختلف منبسط شوند.

مثال‌های انبساط

پرسش: یک برگه استیل در دمای ۲۰ درجه سانتیگراد دارای سایزی است که در شکل زیر نمایش داده شده است.

اگر ضریب انبساط خطی $$10^{-5}\ ^{\circ}C^{-1}$$ باشد، تغییرات در سطح در دمای ۶۰ درجه سانتیگراد چه قدر است؟

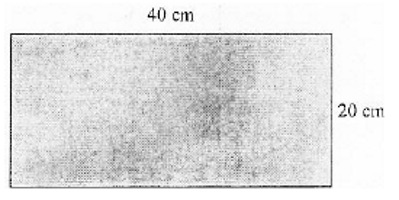
پاسخ: برای محاسبه سطح برگه استیل بعد از افزایش دما باید در ابتدا مساحت صفحه استیل را در دمای بیست درجه سانتیگراد به دست آوریم. بدین ترتیب داریم:

$$A_0=(40) \times (20)=800\ cm^2$$

همچنین ضریب انبساط خطی برابر با $$10^{-5}\ C^{-1}$$ است، بدین ترتیب ضریب انبساط سطحی برابر با $$2 \times 10^{-5}$$ است. تغییرات دما نیز برابر با تفاضل دمای نهایی از دمای اولیه است و داریم:

$$\Delta T=60^{\circ}C-20^{\circ}C=40^{\circ}C$$

بدین ترتیب تغییرات سطح صفحه استیل برابر است با

$$\Delta \mathrm{A}=\beta \mathrm{A}_{0} \Delta \mathrm{T}$$

در رابطه بالا $$\Delta A$$ افزایش سطح، $$\beta$$ ضریب افزایش سطح، $$A_0$$ مساحت اولیه صفحه و $$\Delta T$$ تغییرات دما است. بدین ترتیب $$\Delta A$$ برابر است با:

$$\Delta A=2 \times 10^{-5} \times 800 \times 40=0.64\ cm^2$$

پرسش: ظرفی شیشه‌ای به حجم 4 لیتر را با آب پر کرده و تا دمای 20 درجه سانتی گراد گرم کنید. مقداری آب روی زمین می‌ریزد. ضریب انبساط خطی برای شیشه $$9 \times 10^{-6}\ C^{-1}$$ و ضریب انبساط حجمی برای آب $$2.1 \times 10^{-4}\ C^{-1}$$ است. حجم آب ریخته شده را تعیین کنید.

پاسخ:حجم اولیه ظرف ۴ لیتر و تغییرات دمایی ۲۰ درجه سانتیگراد است. ضریب انبساط خطی برای شیشه را داریم و با توجه به آن می‌توانیم ضریب انبساط حجمی شیشه  را به دست آوریم و داریم:

$$\gamma =3\ \alpha=27 \times 10^{-6}\ ^{\circ}C^{-1}$$

معادله انبساط حجم برابر است با:

$$\begin{aligned}
&\mathrm{V}=\mathrm{V}_{0}+\gamma \mathrm{V} \circ \Delta \mathrm{T} \\
&\mathrm{V}-\mathrm{V}_{0}=\gamma \mathrm{V}_{0} \Delta \mathrm{T} \\
&\Delta \mathrm{V}=\gamma \mathrm{V}_{0} \Delta \mathrm{T}
\end{aligned}$$

بدین ترتیب برای تغییرات حجم محفظه شیشه‌ای داریم:

$$\Delta \mathrm{V}=\gamma \mathrm{V}_{0} \Delta \mathrm{T}=\left(27 \times 10^{-6}\right)(4)(20)=\\
260 \times 10^{-6}=2.160 \times 10^{-3}=0.002160 \text { liters }$$

همچنین تغییرات حجم آب برابر است با:

$$\Delta \mathrm{V}=\gamma \mathrm{V}_0 \Delta \mathrm{T}=\left(2.1 \times 10^{-4}\right)(4)(20)=168 \times 10^{-4}=0.0168 \text { liters }$$

همان طور که مشخص است تغییرات حجم آب از تغییرات حجم محفظه شیشه‌ای بزرگتر است.  بدین ترتیب حجم آب ریخته شده برابر است با:

$$0.0168 \text { liters }-0.002160 \text { liters }=0.01464 \text { liters }=0.015 \text { liters }$$

پرسش: برج ایفل از آهن ساخته شده است و ارتفاع آن حداکثر به ۳۰۰ متر می‌رسد. در طول زمستان دما در فرانسه به ۲ درجه سانتی‌گراد و در تابستان به ۲۵ درجه سانتی‌گراد می‌رسد. تغییرات ارتفاع برج ایفل را بین تابستان تا زمستان محاسبه کنید با توجه به اینکه ضریب انبساط خطی آهن برابر با $$\alpha=10^{-5}\ \frac{1}{^{\circ}C}$$ است.

پاسخ: تغییرات طول در یک جسم برابر با طول اولیه در ضریب انبساط خطی در تغییرات دما است. با توجه به داده‌های اولیه مسئله می‌توان تغییرات طول را به راحتی محاسبه کرد و داریم:

$$\begin{aligned}
& \frac{\Delta L}{L}=\alpha_{\mathrm{L}} \Delta \mathrm{T} \\
& \Delta \mathrm{L}=\alpha_{\mathrm{L}} \mathrm{L} \Delta \mathrm{T} \\
\Delta \mathrm{L}=& 10 \times 10^{-6} \times 300 \times 23=0.69 \mathrm{~m}=69 \mathrm{~cm}
\end{aligned}$$

در این مطلب در مورد انبساط و ویژگی‌های آن صحبت کردیم. همچنین به بررسی ضرایب انبساط خطی، سطحی و حجمی پرداختیم و پارامترهای تاثیر گذار بر آن‌ها را بررسی کردیم.