فرآیندهای ترمودینامیکی — به زبان ساده

در مجموعه مقالات مجله فرادرس با علم ترمودینامیک، و تعاریف آن آشنا شدید. در این مقاله قصد داریم تا با فرآیندهای ترمودینامیکی آشنا شویم و به طور خاص ۴ فرآیند مهم و عمومی را که غالباً در صنعت از آنها استفاده میشود را بررسی کنیم. این چهار فرآیند عبارت هستند از:
- فرآیند هم حجم
- فرآیند هم فشار
- فرآیند هم دما
- فرآیند بی دررو یا آدیاباتیک
با ما در ادامه این مقاله همراه باشید تا با زبانی ساده به تشریح چهار فرآیند فوق، بپردازیم.

تعاریف اولیه
قبل از اینکه به سراغ فرآیندهای مذکور برویم، نیاز است به صورت مختصر با برخی از تعاریف آشنا شویم. توجه داشته باشید که در اینجا جهت دور نشدن از موضوع اصلی، تنها به ارائه تعاریف بسنده کردهایم.
سیستم
به هر جسمی نظیر مایع یا گاز که تحولات گرمایی آن را مطالعه میکنیم، سیستم میگوییم. همچنین هر چیزی که در پیرامون سیستم وجود داشته باشد که با آن در حال تعامل باشد و تبادل انرژی کند، محیط نام دارد.
ترمودینامیک
کمیتهایی که در مقیاسهای بزرگ حالت یک ماده یا سیستم را توصیف میکنند، کمیتهای ماکروسکوپی نام دارند. مجموعه قوانینی که در فرآیندهای گرمایی، کمیتهای ماکروسکوپی را برای یک سیستم به یکدیگر مربوط میکند، علم ترمودینامیک نامیده میشود.
علم ترمودینامیک خود از دل علمی جامعتر به نام فیزیک و مکانیک آماری نتیجه میشود که به مطالعه سیستم، توسط کمیتهای میکروسکوپی میپردازد. در واقع در فیزیک و مکانیک آماری، قوانین ترمودینامیکی از نگاه ریزتر کمیتهای میکروسکوپی نتیجه میشوند.
معادله حالت
رفتار حرارتی یک سیستم توسط متغیرهای (کمیت) ترمودینامیکی توصیف میشود. برای یک گاز ایدهآل، متغیرهای فشار، حجم، دما و تعداد مولکولهای گاز (مول) برای توصیف آن استفاده میشوند. در مقاله «گاز ایده آل — به زبان ساده» دیدیم که معادله حالت یک گاز ایدهآل که در تعادل ترمودینامیکی است به صورت زیر است:
در رابطه فوق، فشار سیستم (گاز)، حجم سیستم، دمای سیستم، تعداد مولهای گاز و ثابت عمومی گازها با مقدار () است. از علوم شیمی پایه به یاد داریم که تعداد مول یک گاز، نسبت جرم گاز به جرم مولی آن تعریف میشود (). منظور از تعادل ترمودینامیکی این است که سیستم به مدت نسبتاً طولانی در یک وضعیت خاص قرار داشته باشد. مشخص است که وضعیت یک سیستم در نتیجه تعامل با محیط بیرون، میتواند تغییر کند. این تغییر وضعیت میتواند سریع، آهسته، زیاد و یا کوچک صورت گیرد.
روش یا چگونگی تغییر وضعیت حالت یک سیستم ترمودینامیکی به وضعیت جدید را فرآیند ترمودینامیکی مینامند. برای تحلیل فرآیندهای ترمودینامیکی، بهتر است که فرآیندها را به صورت شبه استاتیک (ایستاوار) یا غیر شبه استاتیک تقسیمبندی کنیم.
فرآیندهای شبه استاتیک و غیر شبه استاتیک
یک فرآیند شبه استاتیک (ایستاوار یا آرمانی) به یک فرآیند ایدهآل اشاره دارد که در آن تغییر حالت سیستم، بسیار آرام صورت میگیرد. در واقع تغییر وضعیت سیستم آنقدر آرام است که در هر لحظه میتوان سیستم را در تعادل ترمودینامیکی با خود و محیط فرض کرد.
به طور مثال فرض کنید که قصد داریم دمای آب را در فشار ثابت ا اتمسفر () به برسانیم. اگر ظرف حاوی آب را در حمامی بزرگ قرار داده و دمای حمام را به به صورت خیلی آهسته از به افزایش دهیم، توانستهایم دمای آب مذکور را توسط فرآیندی شبهاستاتیک افزایش دهیم. حال اگر ظرف آب را یکباره در حمام قرار دهیم، دمای آب یکباره افزایش پیدا کرده و لذا فرآیندی که طی میکند غیر شبهاستاتیک است.
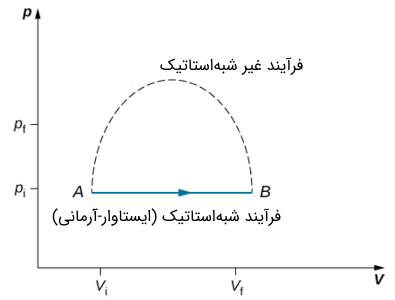
جهت تحلیل راحتتر فرآیندهای ترمودینامیکی، فرآیندهای شبهاستاتیک از اهمیت زیادی برخوردار هستند. چرا که این فرآیندها انقدر آهسته انجام میشوند که با وجود گذشت زمان، میتوان در هر لحظه سیستم را در حال تعادل فرض کرد. تعادل ترمودینامیکی سیستم در هر لحظه از این جهت مهم است که میتوان کمیتهای ماکروسکوپی نظیر دما، فشار و حجم را در هر لحظه از فرآیند محاسبه کرد. بنابراین میتوان فرآیندهای شبه استاتیک را به عنوان مسیری تعریف شده در فضای حالت سیستم نشان داد.
در طبیعت اکثر فرآیندهای ترمودینامیکی که سیستم طی میکند، از نوع غیر شبهاستاتیک است. در واقع بسیاری از فرآیندها را نمیتوان شبهاستاتیک فرض و تحلیل کرد. شکل (1) نمونه یک فرآیند شبه استاتیک و غیر شبه استاتیک را نشان میدهد. از آنجایی که مزیت فرآیندهای شبهاستاتیکی، حل و بررسی تحلیلی است، ما در ادامه این مقاله به فرآیندهای شبهاستاتیک میپردازیم. فرآیند های ترمودینامیکی همحجم، همفشار، همدما و بیدررو را میتوان شبهاستاتیک در نظر گرفت. از قانون اول ترمودینامیک دیدیم که کاری که گاز در یک فرآیند شبه استاتیک انجام میدهد به صورت است.
برای فرآیندهای شبهاستاتیک میتوانیم به راحتی با مشخص کردن کمیتهای ماکروسکوپی حجم، فشار و دما برای چند حالت مختلف، نمودار فرآیند را رسم کرد.
کار
در مقاله «قضیه کار و انرژی — آموزش سریع و ساده» دیدیم که مقدار کاری که یک نیرو طی جابهجایی انجام میدهد به صورت زیر است.
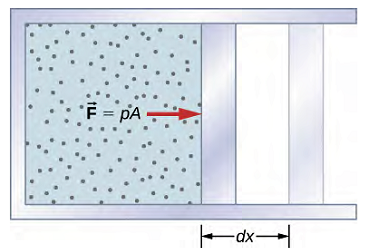
مطابق با شکل فوق، با استفاده از تعریف فشار (نیرو وارد بر سطح ) و در نظر گرفتن () داریم:
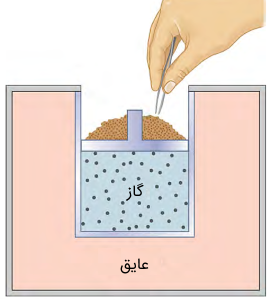
از رابطه فوق مشخص است که سطح زیر منحنی در یک نمودار فشار - حجم برابر با کار انجام شده است. در شکل (3) با کاهش یا افزایش ساچمههای فلزی میتوانیم بر وزن ظرف حاوی ساچمهها تاثیر گذاشته و در نتیجه فشاری که بر سطح پیستون وارد میشود را کنترل کرد. با این کار حجم محفظه داخلی پیستون تغییر کرده و طبق رابطه فوق، کار انجام میشود.
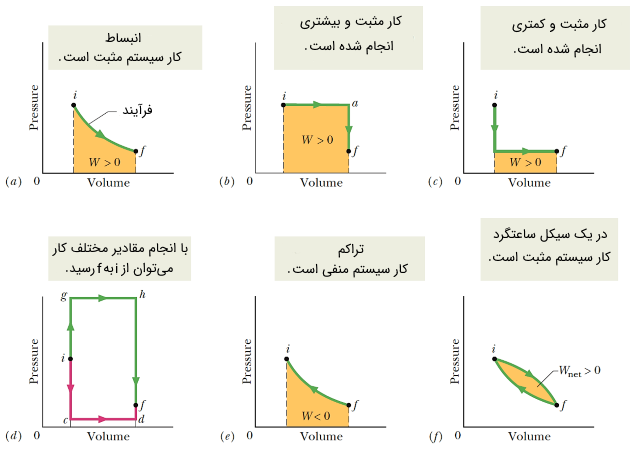
در خصوص علامت کار انجام شده، در بخش فرآیند همفشار توضیحات لازم را ارائه میکنیم. از قوانین پایستگی انرژی میدانیم که کار انجام شده توسط محیط روی سیستم یا سیستم روی محیط از نظر قدرمطلق برابر است و تنها در یک علامت منفی تفاوت دارند. شکل (4) نمودار فشار-حجم را برای فرآیندهای مختلفی نشان میدهد. علامت کار در این شکلها مربوط به کار انجام شده توسط سیستم روی محیط است و کار انجام شده توسط محیط روی سیستم قرینه این مقدار است.
فرآیندهای ترمودینامیکی
همانطور که در مقدمه متن بیان کردیم، معروفترین فرآیندهایی که میتوانیم آنها به صورت شبهاستاتیک بررسی کرده و برای آنها معادله حالت بنویسیم، چهار فرآیند زیر است. شایان ذکر است که این چهار فرآیند در صنعت از اهمیت بسیار زیادی برخوردار هستند.
- فرآیند همحجم
- فرآیند همفشار
- فرآیند همدما
- فرآیند بیدررو (آدیاباتیک)
در ادامه به بررسی فرآیندهای ترمودینامیکی معرفی شده در فوق میپردازیم.
فرآیند هم حجم
همانطور که از نام این فرآیند مشخص است، در طول انجام فرآیند، حجم سیستم ثابت باقی میماند. از رابطه کار مشخص است که در صورت ثابت بودن حجم، سیستم کاری روی محیط (یا محیط روی سیستم) انجام نمیدهد.
از آنجا که فرآیند همحجم فرآیندی شبهاستاتیک است، در هر لحظه میتوان برای آن معادله حالت را به کار برد. از نوشتن معادله حالت برای دو حالت از فرآیند همحجم داریم:
رابطه فوق در سال 1802 میلادی توسط «ژوزف لويس گیلوساک» (Joseph Louis Gay-Lussac) بررسی شد. از قانون اول ترمودینامیک برای یک فرآیند همحجم نتیجه میگیریم:
رابطه فوق بیانگر این است که سیستم (گاز) در فرآیند همحجم تنها با محیط مبادله گرمایی انجام میدهد. پس تغییر انرژی درونی گاز، فقط برابر با گرمای مبادله شده با محیط است.
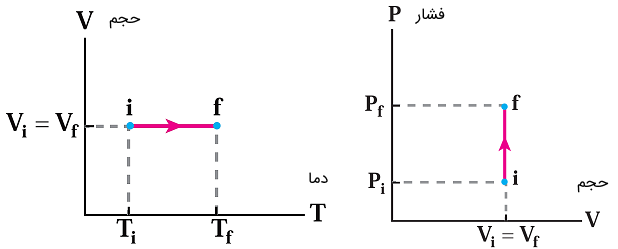
نمودار فرآیند هم حجم
حال به بررسی ۳ نمودار مختلف فرآیند همحجم میپردازیم. در شکلهای فوق نمودار حجم-دما و فشار-حجم برای فرآیند همحجم رسم شدهاند. در این نمودارها دما و فشار افزایش پیدا کرده است. در صورت افزایش دما و فشار یک سیستم در فرآیند هم حجم واضح است که سیستم از محیط گرما گرفته است. اگر سیستم گرمایش را به محیط میداد فشار و دمای آن کاهش پیدا میکرد.
به عنوان مثال، فرآیند پخت غذا در زودپز را میتوان فرآیند همحجم به حساب آورد. از آنجایی که حجم درون زودپز تغییری نمیکند و در آن محکم است، زودپز با گرفتن گرما از محیط (شعله آتش) باعث افزایش خیلی زیاد دما و فشار میشود و در نتیجه غذا سریعتر میپزد. سوپاپ زودپز نیز از این جهت طراحی شده که به هنگام افزایش بیشاز حد فشار، از ترکیدن زودپز جلوگیری کند. حال به نظر شما به چه علت روی قوطیهای اسپری، علامت هشدار دور از گرما و یا هشدار در آتش انداختن ثبت شده است؟

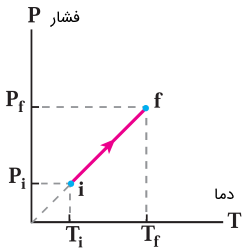
برای رسم نمودار فشار-دمای یک فرآیند همحجم میتوانیم از معادله حالت (فرآیند شبهاستاتیک) استفاده کنیم. از آنجایی که حجم ثابت است، میتوانیم فشار را به صورت زیر، ضریبی از دما (خطی) بنویسیم. در نتیجه نمودار فشار-دما در فرآیند همحجم یک خط با شیب است.
ظرفیت گرمایی مولی در حجم ثابت
در این قسمت میخواهیم مقدار گرمایی را که یک سیستم در فرآیند همحجم با محیط مبادله میکند را به دست آوریم. در مقاله «تعریف گرما و دما در ترمودینامیک — به زبان ساده» دیدیم که مقدار گرمای لازم جهت افزایش دمای کیلوگرم از مادهای در دمای به دمای از رابطه زیر به دست میآید:
با توجه به رابطه که در آن تعداد مول و جرم مولی است، میتوانیم حاصل ضرب را ظرفیت گرمایی مولی تعریف کنیم. در خصوص گازها، بسته به نوع فرآیند، ظرفیت گرمایی مولی میتواند متفاوت باشد. ظرفیت گرمایی مولی (گرمای ویژه مولی) یک گاز در حجم ثابت، برابر با مقدار گرمایی است که باید به یک مول از گاز در حجم ثابت داده شود تا دمای آن به اندازه افزایش پیدا کند. در نتیجه برای یک فرآیند همحجم داریم:
از رابطه فوق، میتوانیم واحد را در سیستم بینالمللی SI، تعریف کنیم. معمولاً میتوان گرمای ویژه در حجم ثابت در فرآیندهای شبه استاتیک (آرمانی یا ایستاوار)، برای گازهای تک اتمی و برای اکثر گازهای دواتمی در نظر گرفت.
فرآیند هم فشار
همانطور که از نام این فرآیند مشخص است، فرآیندی است که تغییر حالت سیستم (گاز) در فشار ثابت رخ میدهد. از آنجایی که فرآیند همفشار را شبهاستاتیک در نظر میگیریم، با نوشتن معادله حالت برای دو حالت مختلف از فرآیند داریم:
رابطه فوق توسط «ژاک شارل» (Jacques Charles) بررسی شد. در یک فرآیند همفشار واضح است که حجم سیستم تغییر میکند. در نتیجه در این فرآیند کار انجام میشود. دقت داشته باشید که کار سیستم روی محیط و کار محیط روی سیستم از نظر عددی برابر است و تنها در یک علامت منفی با یکدیگر تفاوت دارند.
کار محیط (مثلاً پیستون) روی سیستم (گاز) = منفی کار سیستم (گاز) روی محیط (پیستون)
پس کاری که محیط روی سیستم انجام میدهد را میتوانیم به صورت زیر بنویسیم:
در رابطه فوق اگر حجم سیستم افزایش پیدا کند، علامت کار محیط روی سیستم منفی است و اگر حجم کاهش پیدا کند، علامت کار محیط روی سیستم مثبت است. این مطلب را برای کار سیستم روی محیط هم میتوان به کار برد، اما معمولاً در صنعت، منظور از کار، کار محیط روی سیستم است. در ادامه این مقاله نیز، کار محیط روی سیستم را در نظر میگیریم.
نمودار فرآیند هم فشار
در شکل (8) نمودارهای فشار-حجم و فشار-دما برای حالت انبساط یک فرآیند همفشار () رسم شده است.
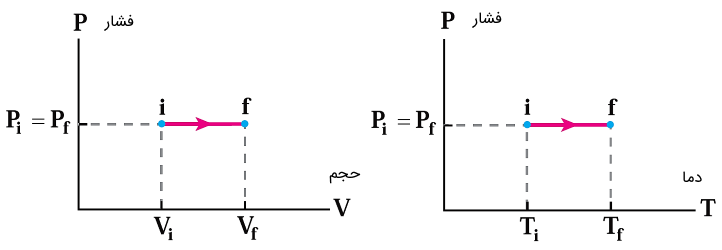
از رابطه انتگرالی کار ()، نتیجه میشود که سطح زیر منحنی نمودار فشار-حجم برابر با کار انجام شده است.
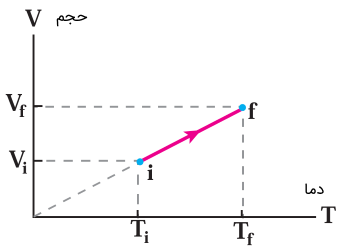
برای رسم نمودار حجم-دما نیز از معادله حالت استفاه میکنیم. طبق این معادله، از آنجایی که فشار سیستم ثابت است، حجم به صورت خطی با دما تغییر میکند.
ظرفیت گرمایی مولی در فشار ثابت
حال میخواهیم مقدار گرمای مبادله شده بین سیستم و محیط را در فرآیند فشار ثابت بررسی کنیم. در اینجا نیز از معادله و تعریف کمیت ظرفیت گرمایی مولی در فشار ثابت، این کار را انجام میدهیم. همانند روندی که در ظرفیت گرمایی مولی در حجم ثابت طی کردیم، در اینجا نیز کمیت را ظرفیت گرمایی مولی نامیده که در فرآیند هم فشار آن را به نشان میدهیم. پس مقدار گرمایی که لازم است تا دمای یک گاز در فرآیند همفشار به اندازه تغییر کند به صورت زیر است:
ظرفیت گرمایی مولی در فشار ثابت (گرمای ویژه مولی در فشار ثابت)، برای گازهایی در فرآیند شبهاستاتیک (آرمانی یا ایستاوار)، برای گازهای تکاتکی و برای گازهای دواتمی است.
از قانون اول ترمودینامیک مشخص است که در فرآیند همفشار، گرما و کار هر دو مبادله میشوند.
با استفاده از تغییر انرژی درونی سیستم (قانون اول ترمودینامیک) میتوانیم نتیجه بگیریم، برای سیستم مشخصی که بتواند از هر دو فرآیند همفشار و همحجم از دمای به دمای برسد، رابطه برقرار است.
فرآیند هم دما
در این فرآیند که آن را همانند دو فرآیند قبلی شبهاستاتیک فرض میکنیم، در طول تغییر وضعیت سیستم (روند فرآیند)، دمای آن ثابت باقی میماند.
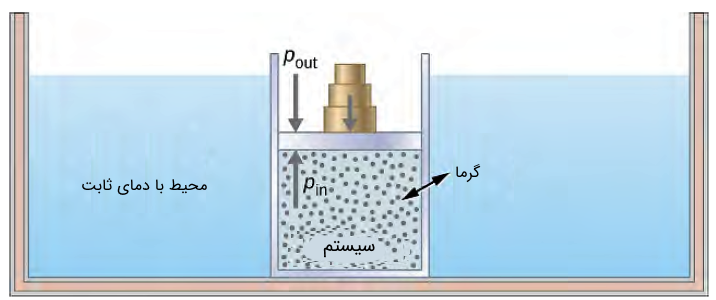
میدانیم که از قانون اول ترمودینامیک، انرژی درونی یک سیستم تابعی از دمای آن است. پس انرژی درونی سیستم برای یک فرآیند شبهاستاتیک همدما صفر است. در نتیجه:
علامت کار انجام شده مطابق با مطلبی که در فرآیند همفشار توضیح داده شد، تعیین میشود. در نتیجه در یک فرآیند تراکمی () همدما، محیط (مثلاً یک پیستون) روی سیستم (گاز) کار انجام داده و در نتیجه مثبت و منفی میشود. منفی بدین منزله است که سیستم (گاز) گرما از دست میدهد. حال اگر یک فرآیند انبساطی () همدما داشته باشیم، سیستم روی محیط کار انجام داده که در نتیجه آن، علامت منفی و علامت مثبت میشود. در یک انبساط همدما، سیستم از محیط گرما می گیرد.
نمودار فرآیند هم دما
نمودارهای فشار-دما و حجم-دما برای یک فرآیند شبهاستاتیک همدما به شکل زیر است:
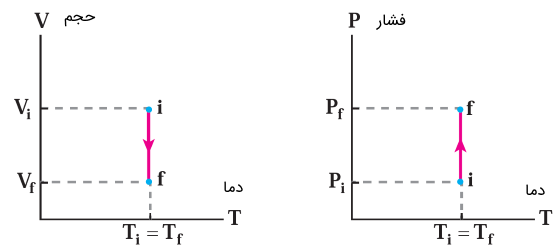
نمودار فشار-حجم برای یک فرآیند شبهاستاتیک همدما فرمی شبیه به شکل نمودار تابع () دارد. چرا که از معادله حالت داریم:
شکل (12) نمودار فرآیند فشار-حجم را برای چهار فرآیند شبه استاتیک همدمای مختلف نشان میدهد.
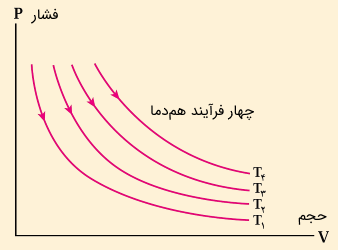
به نظر شما دمای کدام یک از چهار فرآیند فوق بیشتر است؟ برای پاسخ به این سوال میتوانیم از معادله حالت استفاده کنیم. اگر خطی عمود بر محور حجم رسم کنیم که از هر چهار نمودار بگذرد (یک حجم ثابت برای هر چهار فرآیند)، از معادله حالت مشخص است که فرآیندی که فشار بیشتری دارد، دمایش بیشتر است. برای شکل فوق داریم:
از رابطه انتگرالی کار و در نتیجه از مساحت زیر منحنی فشار - حجم میتوان مقدار کار انجام شده را محاسبه کرد. در یک تغییر حجم معین در ۴ فرآیند همدمای شکل (12)، از نظر قدرمطلق کار، کار انجام شده توسط فرآیند همدمای بیشتر است. توجه داشته باشید از آنجایی که در اینجا انبساط () داریم، علامت کاری که محیط روی سیستم انجام میدهد منفی و علامت کاری که سیستم روی محیط انجام میدهد، مثبت است.
فرآیند بی دررو
در مقاله «فرآیند آدیاباتیک — به زبان ساده» به تفصیل آشنا شدید. به طور خلاصه در فرآیند شبهاستاتیک بیدررو یا «آدیاباتیک» (Adiabatic process)، مقدار گرمای مبادله شده بین سیستم و محیط صفر است. فرآیند بیدررو در سیستمهایی که به خوبی عایقبندی (ایزوله) شدهاند رخ میدهد. البته اگر فرآیند آنچنان سریع انجام شود (انبساط یا تراکم) که سیستم (گاز) فرصت تبادل گرما با محیط را پیدا نکند، میتوان فرآیند را بیدررو در نظر گرفت. البته اگر فرآیند خیلی سریع رخ دهد نمیتوان آن را شبهاستاتیک بیدررو در نظر گرفت.
از آنجایی که در فرآیند بیدررو مقدار صفر است، از قانون اول ترمودینامیک برای انرژی درونی سیستم داریم:
از رابطه فوق پی میبریم که اگر حجم سیستم کاهش یابد، یعنی علامت کار انجام شده توسط محیط روی سیستم مثبت باشد، انرژی درونی سیستم به اندازه کار انجام شده افزایش پیدا میکند و اگر فرآیند انبساطی بیدررو داشته باشیم، علامت کار انجام شده توسط محیط روی سیستم منفی و در نتیجه انرژی درونی سیستم به اندازه کار انجام شده کاهش مییابد.
از آنجایی که انرژی درونی یک سیستم تابعی از دما است، با کاهش آن دما کاهش و با افزایش آن دما افزایش پیدا میکند. پس در یک فرآیند بیدررو تراکمی، دما افزایش و در انباسط بیدررو، دما کاهش مییابد. به عنوان مثال، آیا تا به حال در بطری نوشابهای خیلی سرد را خیلی سریع باز کردهاید؟ اگر این کار را کرده باشید مشاهده میکنید که با باز کردن در بطری، نوشابه داخل آن یخ میزند. دلیل این امر را میتوان در مطالب گفته شده در بالا یافت. از آنجایی که در بطری را سریع باز میکنیم، میتوانیم فرآیند انجام شده روی سیستم (نوشابه گازدار) را بی دررو فرض کنیم. از آنجایی که با باز کردن در بطری، حجم سیستم افزایش مییابد، مطابق با قانون اول ترمودینامیک برای فرآیند بیدررو، انرژی درونی آن کاهش پیدا کرده و در نتیجه دما کاهش مییابد.

نمودار فشار-حجم فرآیند بیدررو
نمودار فشار-حجم برای فرآیند بیدرو منحنی شبیه به نمودار فشار-حجم فرآیند همدما است. مطابق با شکل زیر در یک انبساط بیدررو که دما در آن از به کاهش پیدا میکند، منحنی فشار-حجم آن زیر منحنی فشار-حجم فرآیندی همدمایی است که در دمای انجام میشود.
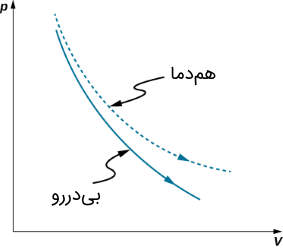
از نمودار شکل فوق مشخص است که سطح زیر منحنی که مصداق کار تلقی میشود، برای فرآیند همدما بیشتر است.
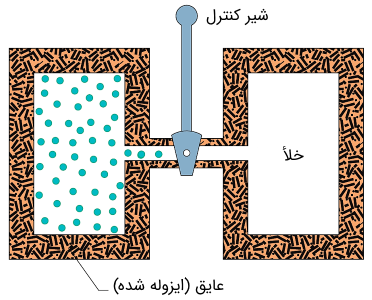
انبساط آزاد
فرآیند انبساط آزاد را میتوان فرآیندی بیدررو به حساب آورد که کار انجام شده در آن نیز صفر است. برای اینکه درک بهتری از این فرآیند داشته باشید، به شکل (۱۵) دقت کنید. در اینجا سیستمی داریم که به شدت از محیط بیرون ایزوله بوده و حجم کل آن ثابت است. با باز کردن شیر، گاز در سراسر سیستم پخش میشود. دقت داشته باشید که در اینجا تنها فشردگی گاز درون محفظه کمتر شده و حجم سیستم در قبال محیط تغییری نداشته و در نتیجه کاری انجام نمیشود.
انرژی درونی
از قانون اول ترمودینامیک آموختیم که انرژی درونی یک سیستم به صورت است. حال شکل (16) را در نظر بگیرید. هر چهار فرآیند ab، ac، ad و ae دمای سیستم را از به تغییر دادهاند. میتوان ثابت کرد که تغییر انرژی درونی در تمامی چهار فرآیند فوق یا هر فرآیند دیگری که دمای سیستم را از به تغییر دهد، برابر با مقدار زیر است:
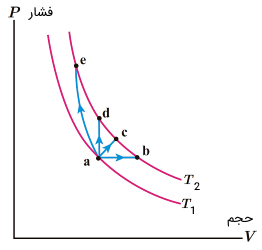
برای اثبات رابطه فوق، از نتیجه قانون اول ترمودینامیک استفاده میکنیم. میدانیم که انرژی درونی یک سیستم (گاز) در فرآیندی شبهاستاتیک تنها تابعی از دمای آن است. از آنجایی که در هر چهار فرآیند شکل (16) دماهای اولیه و نهایی یکسان است، پس کافی است تغییر انرژی درونی یکی از فرآیندها را محاسبه و آن را برای دیگر فرآیندها نیز استفاده کنیم. سادهترین فرآیندی که میتوان آن را انتخاب کرد، فرآیند همحجم است، چرا که کار () در آن صفر است و گرمای () به راحتی از رابطه زیر به دست میآید:
از رابطه فوق نتیجه میشود که کار انجام شده در فرآیند شبهاستاتیک بیدررو برابر با مقدار فوق است. یادآور میشویم که در فرآیند بی دررو، گرمایی مبادله نمیشود و است. پیشتر گفتیم که برای یک سیستم که فرآیندی شبهاستاتیک را طی میکند، رابطه برقرار است. از مطلب فوق میتوانیم برای اثبات آن به شکل زیر استفاده کنیم (فرآیند همفشار، انبساطی در نظر گرفته میشود):
از آنجایی که دو فرآیند فوق شبهاستاتیک در نظر گرفته میشوند، از معادله حالت داریم:
در نتیجه:
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:













سلام،
همه صحبت ما این بود که فرآیند بی در رو شبه استاتیک است. در متن پاراگراف اول فرآیند بی در رو آیا این دو جمله متناقض نیستند؟
“البته اگر فرآیند آنچنان سریع انجام شود (انبساط یا تراکم) که سیستم (گاز) فرصت تبادل گرما با محیط را پیدا نکند، میتوان فرآیند را بیدررو در نظر گرفت. البته اگر فرآیند خیلی سریع رخ دهد نمیتوان آن را شبهاستاتیک بیدررو در نظر گرفت.”
با سلام،
به این نکته توجه داشته باشید که فرایند بیدررو را در برخی مواقع، به خصوص دینامیک سیالات، میتوانیم به صورت فرایند شبهاستاتیک در نظر بگیریم.
با تشکر از همراهی شما با مجله فرادرس
جسارتا یک مشکل در یکی از تصاویر بود که گفته بود در نمودار P_V کار انجام شده در سیکل ساعتگردمثبت است اما اینطور نیست
با سلام،
در فیزیک، علامت کار انجام شده روی سیستم در چرخه ترمودینامیکی ساعتگرد در نمودار PV بستگی به قرارداد تعیین شده دارد. در برخی کتابهای درسی، علامت قراردادی و مورد توافق برای کار به گونهای تعریف میشود که کار انجام شده روی سیستم مثبت در نظر گرفته شود. در مقابل، کار انجام شده توسط سیستم را منفی در نظر میگیرند. از این قرارداد به طور معمول در فیزیک استفاده میشود.
بنابراین، اگر از این قرارداد استفاده کنید، در چرخه ترمودینامیکی ساعتگرد در نمودار PV، کار انجام شده روی سیستم را منفی در نظر خواهیم گرفت. گرچه، توجه به این نکته مهم است که کتابهای درسی متفاوت قرارداهای مختلفی دارند.
عالی بود.ممنونم
سلام و عرض ادب
میشه توضیح بدید چرا نمودار فرایند همدما بالاتر از فرایند بی دررو قرار میگیره؟شکل 14منظورمه
سلام یه سوال داشتم ممنون میشم جواب بدید.
چگونه میتوان ضریب عملکرد یخچال را افزایش داد.برای ترمودینامیکه.
سلام. یک سوال. دقیقا متن سوال همین بود.
در تحول …… تمام گرما به کار تبدیل میشود.
۱) آدیباباتیک
۲) فشار ثابت
۳) دما ثابت
۴) حجم ثابت
سلام و روز شما به خیر؛
پاسخ سوال شما فرآیند هم دما است زیرا تغییرات انرژی درونی سیستم با تغییرات دما مرتبط است و در یک فرآیند همدما، تغییرات دما برابر با صفر است و در نتیجه طبق رابطه ΔU=W+Q مقدار ΔU یا تغییرات درونی جسم صفر است و تمام گرما به کار تبدیل میشود.
از اینکه با فرادرس همراه هستید، خرسندیم.
بسیارجامع وخلاصه بود دست خوش
سلام
وقتتون بخیر
میشه راجع به نمودار v_t و p_t فرایند آدیاباتیک هم توضیح بدین