لگاریتم و ویژگی های آن – به زبان ساده

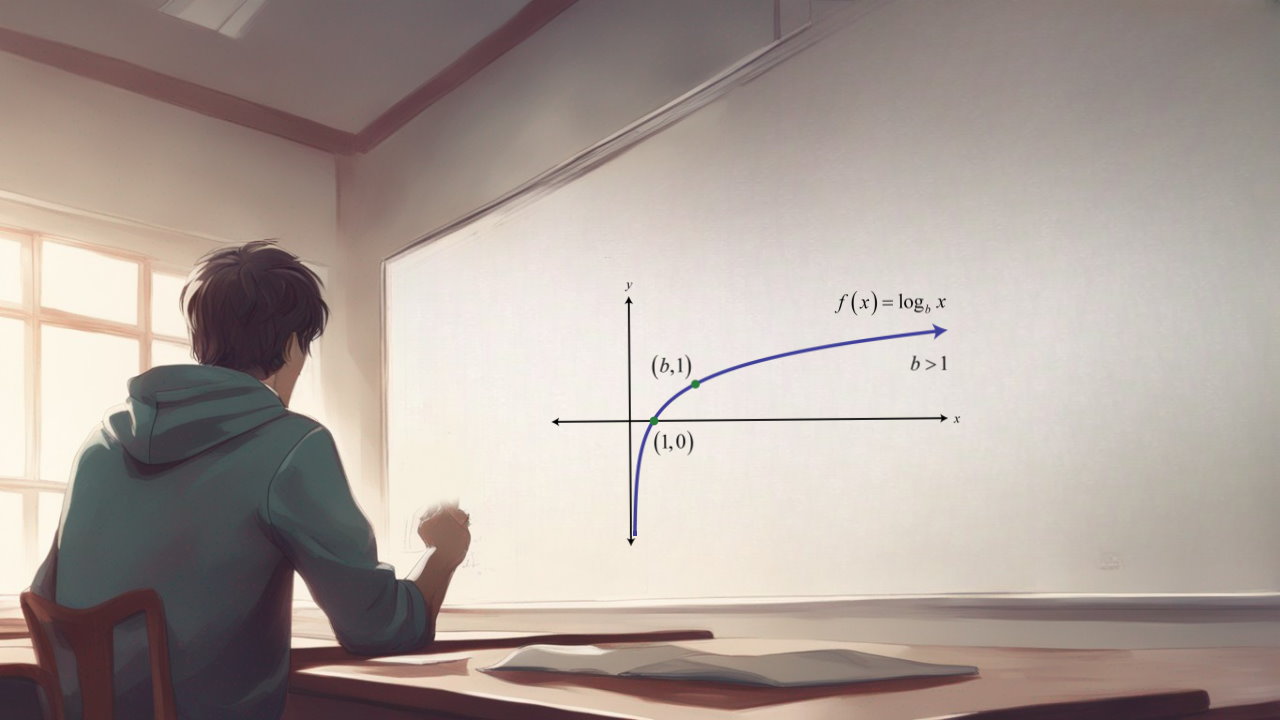
لگاریتم، تابع وارون عبارت نمایی است. توابع لگاریتمی، کاربرد زیادی در حوزه ریاضی و علوم کاربردی مرتبط با آن دارند. این توابع معمولا با فرم ساده و به صورت f(x)=logax نمایش داده میشوند. a، مبنای لگاریتم است. در حالت پیشفرض، این مبنا برابر با 10 است. اگر مبنای لگاریتم برابر با ۲/۷۱۸۲۸ (عدد اویلر) باشد، به آن لگاریتم طبیعی میگوییم و با فرم f(x)=lnx نمایش میدهیم. توابع لگاریتمی، خصوصیات و ویژگیهای زیادی دارند. در این مقاله از مجل فرادرس قصد داریم به معرفی این ویژگیها و حل چندین مثال متنوع بپردازیم.
هدف از تعریف تابع لگاریتم چیست ؟
انگیزهٔ ساخت لگاریتم، داشتن وارون تابع توان است. برای نمونه، توان سوم ۲، ۸ است چون ۸ = ۲ × ۲ × ۲ = ۲۳ پس لگاریتم ۸ در پایهٔ ۲، ۳ میشود.
مفهوم امروزی لگاریتم در نتیجه کارهای اویلر در قرن ۱۸ میلادی توسعه یافته است. اویلر نخستین کسی بود که مفهوم لگاریتم را به مفهوم تابع نمایی پیوند داد. در سادهترین حالت، یک لگاریتم پاسخ سوال زیر را می دهد:
چه تعداد از یک عدد را باید در خودش ضرب کنیم تا عدد دیگری را به دست آوریم؟
مثال: چه تعداد از عدد 2 را باید در هم ضرب کنیم تا عدد 8 به دست بیاید؟
پاسخ: 8 = 2 × 2 × 2، پس باید 3 بار 2 را در خود ضرب کنیم تا عدد 8 بدست آید. پس لگاریتم برابر 3 است.
کلمه لگاریتم
«لگاریتم» عبارتی است که ریاضیدان اسکاتلندی، جان نپر (1617 - 1550) آن را ساخته است. در زبان یونانی کلمه لوگوس به معنی «نسبت، میزان یا واژه» و آریتموس به معنی «عدد» است، ترکیب این دو واژه با هم به معنی «نسبت - عدد» میشود.
چگونه لگاریتم را بنویسیم
دانستیم که بدین جهت لگاریتم 8 برابر با 3 است که تعداد دفعاتی که باید 2 را در خودش ضرب کنیم تا عدد 8 به دست آید، 3 است. این مفهوم را به شکل زیر مینویسیم:
log2(8) = 3
پس این دو عمل باهم برابرند:
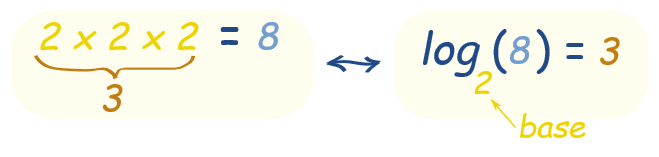
عددی که ضرب میکنیم، همان «پایه» است. پس میشود گفت:
- لگاریتم 8 با پایه 2 برابر است با 3
- یا لگاریتم پایه دو 8 برابر است با 3
- یا پایه 2 لگاریتم 8 برابر است با 3
دقت کنید که در موضوع لگاریتم با سه نوع عدد سر و کار داریم:
- پایه یعنی عددی که ما ضرب میکنیم (در این مثال 2 بود)
- تعداد دفعاتی که عدد پایه را در خود ضرب میکنیم (3 بار، که همان لگاریتم است)
- عددی که میخواهیم در انتها بگیریم (عدد 8)
مثال های بیشتر
مثال: لگاریتم زیر را حساب کنید.
log5(625)
سوال میپرسد: چه تعداد 5 باید در هم ضرب شوند تا عدد 625 به دست آید؟ پاسخ چنین است:
625 = 5 × 5 × 5 × 5
پس ما به 4 تا پنج نیاز داریم. بنابراین:
log5(625) = 4
مثال: لگاریتم زیر را حساب کنید:
log2(64)
سوال میپرسد: چه تعداد 2 باید در هم ضرب شوند تا عدد 64 به دست آید؟ برای محاسبه داریم:
64 = 2 × 2 × 2 × 2 × 2 × 2
پس ما به 6 تا دو نیاز داریم:
log2(64) = 6
توانها
توانها و لگاریتمها مرتبط هستند، در ادامه نحوه ارتباط این دو را بررسی میکنیم.

صورت سوال یک لگاریتم به این شکل است:
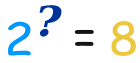
و پاسخ آن نیز به صورت زیر است:
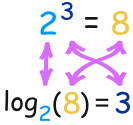
لگاریتم برایمان مشخص میکند که توان چه عددی است. در مثال ذکر شده پایه برابر 2 و توان برابر 3 است:

پس لگاریتم دپاسخ سوال زیر را نیز میدهد که به چه توانی برای یک عدد احتیاج داریم تا آن به عدد مشخص دیگری تغییر یابد. به طور کلی رابطه توان و لگاریتم به شکل زیر است:
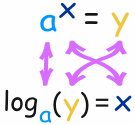
مثال: لگاریتم زیر را بیابید:
log10(100)
پاسخ:
102 = 100
پس توانی به مقدار 2 نیاز است که عدد 10 را به 100 تغییر دهیم:
log10(100) = 2
مثال: لگاریتم زیر را پیدا کنید:
log3(81)
پاسخ:
34 = 81
پس توانی به اندازه 4 نیاز است که عدد 3 به 81 تغییر یابد:
log3(81) = 4
لگاریتمهای معمولی: پایه 10
گاهی اوقات یک لگاریتم را بدون پایه مینویسند، مانند:
log(100)
این معمولاً به این معنی است که پایه برابر 10 است.
به این لگاریتم، یک «لگاریتم معمولی» گفته میشود، مهندسان به این لگاریتم علاقه خاصی دارند. این لگاریتم در ماشینحسابها با عبارت log مشخص میشود.

این لگاریتم نشان میدهد که چند بار باید عدد 10 را در خود ضرب کنیم، تا عدد مورد نظرمان به دست آید.
مثال:
log(1000) = log10(1000) = 3
لگاریتمهای طبیعی: لگاریتم در پایه e
پایه دیگری که معمولاً مورد استفاده قرار میگیرد، عدد اویلر (e) است، که مقدار آن حدوداً برابر با 2.71828 است.
به این لگاریتم «لگاریتم طبیعی» گفته میشود. ریاضیدانان از این لگاریتم استفاده فراوانی میکنند. این لگاریتم بر روی یک ماشین حساب، با کلمه ln مشخص میشود.
این لگاریتم یعنی چند بار باید عدد e در خودش ضرب شود تا عدد مورد نظرمان به دست آید.
مثال:
ln(7.389) = loge(7.389) ≈ 2
چون که
2.718282 ≈ 7.389
موارد سردرگم کننده
ریاضی دانان از «log» (به جای «ln») به عنوان لگاریتم طبیعی استفاده میکنند. این مسئله ممکن است ما را گمراه کند:

پس، مراقب باشید که اگر با log برخورد داشتید، بدانید پایه مورد استفاده چیست.
لگاریتمهای اعشاری
ما تا اینجا در تمامی مثالهای خود از لگاریتم های اعداد صحیح استفاده کردیم (مانند 2 یا 3)؛ اما لگاریتمها میتوانند مقدار اعشاری مانند 2.5، یا 6.081، و غیره نیز داشته باشند.
مثال:مقدار لگاریتم زیر را پیدا کنید:
log10(26)
از ماشین حساب استفاده کنید، عدد 26 را وارد کرده، دکمه log را فشار دهید.
پاسخ برابر است با: ...1.41497
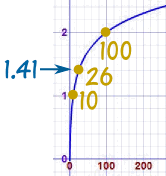
لگاریتم به ما می گوید که 26 = ...101.41497 (10 با توان ...1.41497 برابر 26 است)
این لگاریتم روی نمودار به شکل زیر است، دقت کنید که چگونه خط به شکل منحنی و ناشکسته است.
لگاریتمهای منفی
شاید از خود بپرسید لگاریتم منفی به چه معنی است. چون تا آنجا که آموختیم لگاریتم ها به ضرب مربوط هستند. پاسخ این است که باید توجه کنید در مقابل ضرب چه داریم؟ مفهوم معکوس ضرب، تقسیم است.
در مورد لگاریتم نیز میتوانیم یک تقسیم داشته باشیم. یک لگاریتم منفی به این معنی است که یک عدد را چند بار باید بر خود تقسیم کنیم تا عدد مورد نظر به دست آید.
مثال: لگاریتم زیر را بیابید:
log8(0.125)
میدانیم که:
1 ÷ 8 = 0.125
پس:
log8(0.125) = −1
یا می توانیم چندین تقسیم داشته باشیم:
مثال: لگاریتم زیر را پیدا کنید:
log5(0.008)
پاسخ:
1 ÷ 5 ÷ 5 ÷ 5 = 5−3
پس:
log5(0.008) = −3
همه اینها منطقی هستند
ضربها و تقسیمها همگی قسمتهایی از یک الگوی ساده است. بیایید به چند لگاریتم پایه 10 بعنوان مثال نگاه کنیم:
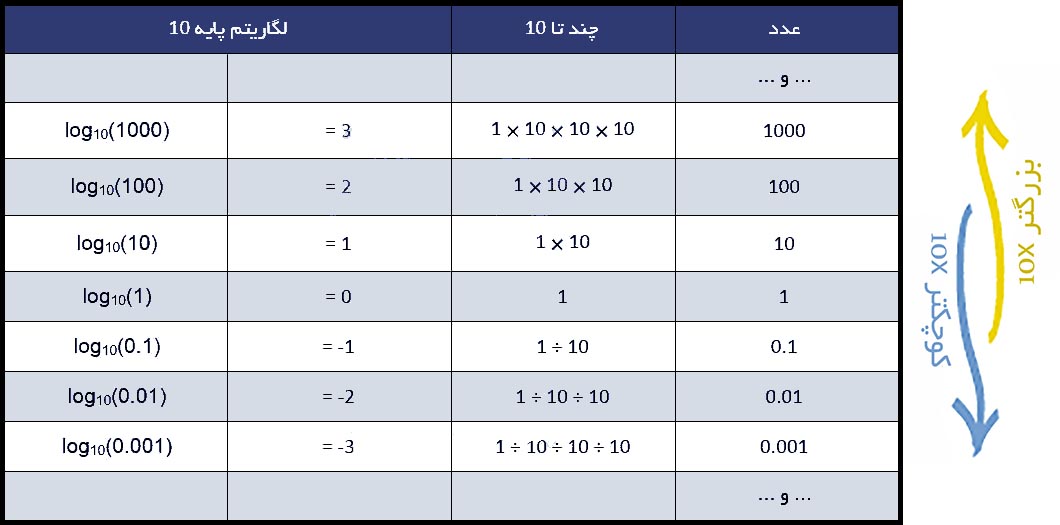
با نگاه به جدول، ببینید که لگاریتم های مثبت، صفر و یا منفی همگی از روی یک الگوی ساده محاسبه میشوند.
==












در متن در مورد لگاریتم منفی گفته شده:”ک لگاریتم منفی به این معنی است که یک عدد را چند بار باید بر خود تقسیم کنیم تا عدد مورد نظر به دست آید.”
اما در واقع مطلب این هست که چند بار عدد 1 به پایه تقسیم شده. به نظر من گیج کننده بود این قسمت.
توی اولین تقسیم مقدارش میشه ۱ مثلا ۵/۵ میشه ۱ که طبق قرارداد این رو همون عدد به توان ۰ در نظر میگیریم از دومی که تقسیم میکنیم مقدارش منفی میشه. برای راحتی و اشتباه نشدن از همون اول ۱ رو تقسیم میکنیم که تعداد تقسیم ها رو درست بشماریم
عالی. مفهوم را خیلی خوب توضیح دادید.
سلام واقعا عالی بود.
سلام
لگاریتم بدون توان رو چطور حساب کنیم مثلا میگه log(10 .
سلام عالی بود برای اولین بار بالگاریتم آشنا شدم ولی کاملا متوجه شدم
تشکر فراوان
عالی علی
ممنونم توضیحات به زبان ساده و روان گفته شده بود
ممنونم خیلی قابل فهم بود
از مقاله بسیار کاربردی و در عین حال ساده شما بسیار بسیار ممنونم.
موفق باشید
و حتما ادامه دهید
با سلام بسیار عالی و روان بود. تنها نکته این که در قسمت جدول موارد گمراه کننده به نظر میرسد در خانه مثال سطر اول به جای Log بایدLn نوشته شود.
با سلام،
متن بازبینی و ایرادی مشاهده نشد،
با تشکر از همراهی شما با مجله فرادرس
سلام من مبحث رو در سال کنکور یادمه که استاد فراهانی به ما تدریس میکردن به روش داستانی ،هنوز ک هنوزه مگ این مبحث رو به خاطر دارم ،واقعا قدر دان تدریس ایشون و اموزشگاه فرزانه ۲چ هستم
سلام و سپاس
– در قسمت “لگاریتمهای طبیعی”، در آخرین خط، توان 2 جا افتاده.
– در قسمت “لگاریتمهای اعشاری”، فکر میکنم نمودار لگاریتم ایراد داره.نباید محور yها رو قطع کنه.
سلام.
مورد اول اصلاح شد. اما مورد دوم، نمودار تقریبی رسم شده و آن را قطع نکرده است. نمودار در منفی بینهایت به محور عمودی میرسد.
سپاس از همراهی و بازخوردتان.
خیلی مفید و مختصر و با زبان ساده توضیح داده شده . خیلی ممنونم
عالی بود
خیلی ممنون واقعا عالی و مفهومی????❤??
سلام
واقعا مفید بود و خیلی عالی توضیح داده بودید
خیلی ممنون
خیلی عالی و مفهومی ✨
سلام.
عالی توضیح دادید.
سپاسگزارم.
ممنونم خیلی بهم کمک شد
کلا ریاضیات رو فراموش کرده بودم
ولی با کمک شما ب سادگی همه رو یادم اومد ?
سلام ببخشید تو شیمی چطور حساب میشه
سلام
تا حالا ب این زیبای ریاضی یاد نگرفته بودم
این مولفین کتاب های ریاضی فکر میکنن چون خودشون بلد هستن بقیم راحت بلد میشن
اره والا
درود بی پایان
بسیار ممنونم و تشکر میکنم از وبسایت عالیتون که مطالب ره به زبانی ساده و روان توضیح میدهید.
موفق باشید
ممنون متوجه داستان شدم و مشکلم حل شد.
بسیار عالی لذت بردم خدا خیرتون بده الهی
بسیار عالی و مفید ، سپاسگزارم
با سلام و دروود به شما اساتید عزیز فرادرس .
در ارائه مطالب علمی نسبت به دیگر منابع ، بسیار مفهومی و مستدل عمل کردید، دروود فراوان به شما.
برای تفهیم چگونگی بدست آوردن لگاریتمهای منفی حتما باید ابتدا از تقسیم عدد ۱ بر مبنا استفاده کرد تا تعداد اعداد توان ( توان منفی ) مشخص شود …. کمی برای من و امثال من نامفهومه . ممنون میشم قسمت توانهای منفی لگاریتمی را کمی بیشتر باز کنید
درود برشما-بارها یا همان روش قدیمی که بما در 60 سال قبل لگاریتم دوپویی(مدارس فرانسه ان زمان) را اموخته بودند سعی کردم برای سئوالات نوه ام توضیح دهم ولی احساس می کردم موضوع برایش ابهاماتی دارد.برحسب تصادف این سایت مفید را دیدم .چقدر سلیس وروان (برخلاف ان لغات ناما”نوس دوره ما) وزیبا گفته اید.ونوه ام فقط با یکبار خواندن متن شما- بجای 4 بار توضیحات من متوجه شد.خواستم تشکر نمایم.موفق وپیروز باشید.
سلام خیلی عالی بود ولی اگر از لگاریتم های رادیکالی و کسری هم مثال می زدید بهتر بود با تشکر
با سلام و تشکر از توجه شما به مجله فرادرس،
برای آشنایی با نحوه محاسبه لگاریتم برای کسرها و عبارتهای تواندار نوشتار لگاریتم و خصوصیات آن — به زبان ساده را مطالعه فرمایید.
از اینکه همراه مجله فرادرس هستید بسیار سپاسگزاریم.
سربلند و پاینده باشید.
واقعا يه همچين مواقعی معلوم ميشه که در سيستم آموزش و پرورش چقدر داره وقت و عمر و سرمايه و استعداد و انگيزه و … بچه های اين مملکت به آسانی به باد ميره.
من فوق ليسانسم و در طول 18 سال درس خوندن، تعداد کمی معلم بدرد بخور داشتم. اگر اکثر معلمها اينجوری مطالب رو برامون ساده و به زبان آدميزاد توضيح ميدادن، الان دوباره کشورمون به راحتی به همون درخشندگی علمی اش در تاريخ دست پيدا ميکرد.
واقعا درست ميگن اگر ميخواهيد کشوری رو بسازيد، معلمهاش رو بسازيد.
استاد مسعود عبدالرحیمی، دست شما درد نکنه با اين روش عاليتون. خداوند متعال عمر طولانی و با عزت به شما معلمان با دانش عطا فرمايد
سلام
حق باشماست اما توجه کنید
که مطالب فوق که به بهترین و جذاب ترین وآسان ترین شکل لگاریتم را آموزش داده ترجمه یک سایت خارجی است.که منبعش هم ذکر شده
با این وجود ترجمه سلیس و روان جای تقدیر وتشکر دارد.
در مورد سیستم آموزشی:
متاسفانه در سال های اخیر به جای توضیح مسائل درسی از روش فعالی وحل مسأله استفاده شده است که یعنی نمی توان فقط به کتاب درسی بسنده کرد،اگر به کتاب های درسی دهه ۶۰ و۷۰ نگاه کنید مبینید که بیشتر مفهومی هستند
خدا خیرتان بده . خیلی برام مفید بود. حالا می فهمم ریاضی درس شیرینیه یعنی چی.
سلام. واقعا ممنون. خیلی عالی و مفهومی توضیح دادید. (برعکس ویکیپدیا). تصاویری هم که طراحی کردید، خیلی کمک کرد. همیشه موفق و پیروز باشید. :)))
سلام خیلی ممنون از آموزش خوب صریح و شیوا ،خیلی مشکلم تو قسمت ریاضی درس هام با شما حل شد ممنونم از شما و سایت خوبتون
تمامی اموزش های شما که در اینترنت قرار داده شد وفقط با یک سرچ کردن راحت بصورت رایگان از سایت فرادرس بالا می یاد واقعا زیبا و اسان هستند واقعا فن بیان بالایی را بکار می برید و خیلی زیبا توضیح ممنون خداخیرتون بده من که زبان برنامه نویسی را از این سایت خریداری کردم همش یک جا هایی برای اینکه ریاضی ها ومفاهیم از یادم رفته این آموزش ها کمک شایانی بهم کرده ممنون
آدم خندش میگیره که این سایت از کتابای چرت و آموزش و پرورش خیلی بهتره ..ممنونم اجرتان با خدا
خیلی خوب .
خدا خیرتون بده . اینهمه ریاضی خوانده ایم در دبیرستان و دانشگاه هیچ کدوم اینقدر قشنگ توضیح نداده اند.
نذری آموزشی تون هم قبول باشه اساتید محترم. خیلی استفاده کردم.
همیشه توی ریاضی ضعیف بودم، ضعیف که چه عرض کنم اصلا نمیفهمیدمش. به این میگند توضیح به این میگند روش درس دادن. کارتون حرف نداره.
راستی اگه یه افزونه تست مثل سایت بریلیانت که انگلیسی هست رو این مجله و آموزش ها بزارید دیگه فوق العاده میشه
سلام.عالی هستید. به کارتون افتخار کنید و با قدرت برید جلو. محمد.
سلام و درود، نحوه اموزش واقعا عالی بود.
خدا قوت
سلام دوستان، واقعا عالی بود و استفاده کردم. چطور میتونم جزوه ها و کلیپهای آموزشی تون رو تهیه کنم؟
بسیار عالی توضیح داده، و واقعا درک مطلب رو آسان کرده،
يني 25 ساله از لگاريتم هيچي نميفهميدم تازه فهميدم چيه!!! چقدرم ساده محاسبه ميشه…
فقط لگاريتم منفي رو كاش مثل عاديش تفهيم ميكردين
مدرسه اگر از اول اگر مفهوم اشو درس ميدادن ميگرفتيم
هيچموقع معني اعمال رياضي رو نميگن و دوست دارن مثل كتب ديني فقط ربات وار يك چيزايي رو محاسبه كنيم…
سلام مطالب خیلی خوبی بود
من چندتا تمرین حل کرد یه حایی دیدم به جایی تساوی زیر را دیدم که نفهمیدم جطوری شده اکه توضیح بدید ممنون میشم
log5=1-log2
سلام.
با توجه به رابطه log(x/y)=logx-logy میتوان نوشت: log(10/2)=log10-log2 و ازآنجاییکه log10=1، خواهیم داشت: log5=1-log2.
سلام
عالی بود
توضیحات مربوط به کلید مرتبط با لگاریتم در ماشین حساب ایده جالبی بود
با درود و وقت بخیر ! بسیار سپاسگزارم ! ریاضیات را فراموش کرده بودم و مطلب آموزشی شما درباره لگاریتم برایم یادآوری کرد و دوباره آموزی نمودم.
بسیار عالی و مفهومی
خسته نباشید……
عالی بود متشکرم
سلام. عالی بود. مرسی
سلام .بسیار عالی بود. شما هم مثال پارامتری زدین .هم مثال عددی که تفهیم رو بسیار ساده کرده .عالی
خدا خيرتون بده واقعا ممنونم ازتون
خدا خیرتون بده چند وقتی بود کلا همه مفاهیم یادم رفته بود..تو سایت شما خوب یاداوری و تفهیم شد…
سلام عالی هستین…… اجرکم من الله…
سلام ممنون خیلی خوب اموزش دادید خیلی خوب میشه آموزش های بیشتری تو مباحث ریاضی ، کامپیوتر و الگوریتم منتشر کنید
LOL
خدایی دمتون گرم بعد 12 سال بالاخره پایه لگاریتمو متوجه شدم ینی حالا میفهمم این سیستم آموزشی به ما تو دبیرستان هیچی یاد نداده! همه میگن دانش آموزا درس نمیخونن اما کیه كه ندونه اشتیاق و انگیزه و محرکی ندارن! اگه به ما هم اینجوری درس میدادن لازم نبود سه سال واسه ریاضی معطل مدرک دیپلم باشیم آخرشم با درس جایگزین تو شبانه پاس کنیم!
خیلی عالی بود . ممنون
واقعا عالی بود
واقعاااا ممنوووون عالی بود.کاش به ما هم ریاضی رو اینجوری یاد داده بودن
من صبح امتحان ریاضی داشتم و هرچی جزوه میخوندم و کتابو میخوندم حالیم نمیشد:)) الان با یه نگاه ساده به اینجا یجورایی فهمیدم و برگم رو سفید نمیدم^_^ ممنونم
سلام لگاریتم 80001 چجوری به دست می آید
خدا اجرتون بده من نمیدونم ما نمیفهمیدیم یا معلما حالیشون نبود خلاصه بعد چند سال بلاخره یزره از لوگاریتم فهمیدم
سلام ، توان یه اسمی داره ، اسمش چیه؟
این همه سال کتاب و جزوه خوندیم اندازه این چند صفحه تفهیممون نکرد. حیف این همه سال، حیف این همه وقت! ممنون
خیلی مفید و اموزنده بود با تشکر از زحمات شما
ممنون از آموزش بسیار پایه ای شما .
با تشکر از شما
من در مدرسه ریاضی میخوندم ولی هیچ وقت نفهمیدم میتونه مطالب ریاضی به این سادگی باشه
بعد از بیست سال فاصله از درس به دلایلی تحقیقی مجبورم رو فیزیک و ریاضی مطالعه داشته باشم که این مقدمات بسیار به من کمک کردند.
باز هم ممنون