نظریه جنبشی گاز‌ها — از صفر تا صد

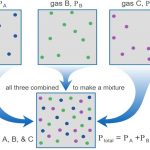
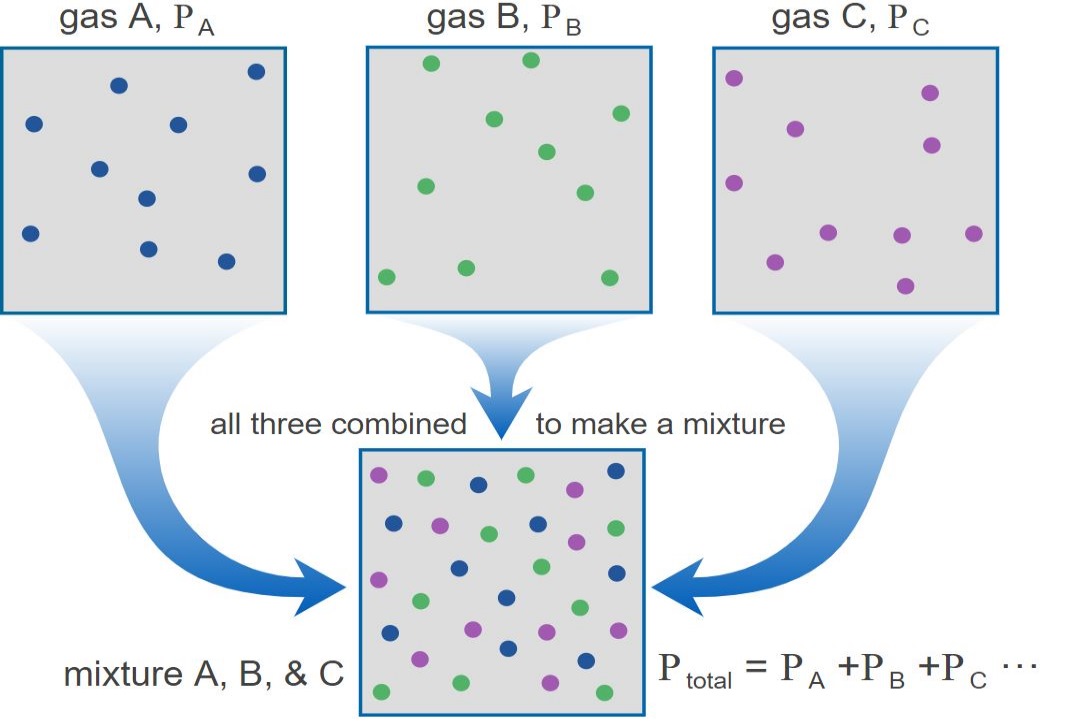
در مکانیک نیوتنی، فشار به صورت نیروی عمود وارد به سطح تعریف می‌شود. حال این سوال مطرح می‌شود که فشار در گاز‌ها به چه صورت تعریف می‌شود؟ در این مطلب قصد داریم تا با استفاده از نظریه جنبشی گاز‌ها به این پرسش پاسخ دهیم.

فشار از دیدگاه مولکولی

فشار در گاز‌ها با استفاده از نظریه جنبشی گاز‌ها تعریف می‌شود. این نظریه می‌گوید، فشار معادل با میانگین نیرو‌یی است که مولکول‌های یک گاز به دیواره مخزن وارد می‌کنند. در ابتدا همانند شکل زیر، مخزنی را در نظر بگیرید که حاوی N مولکول از یک گاز است.

فیلم آموزش فیزیک پایه 3 – جامع و کاربردی در فرادرس

کلیک کنید

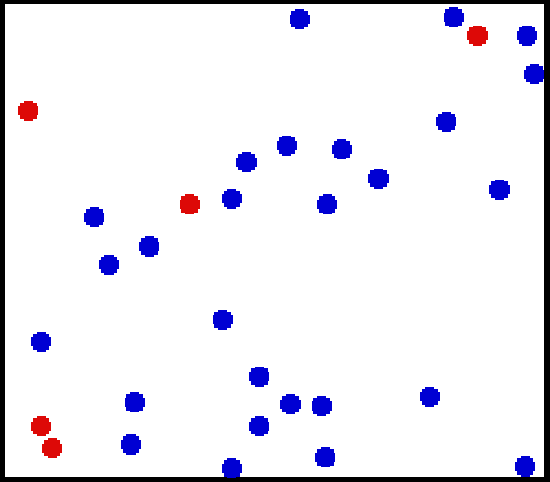
فرض کنید حجم مخزن برابر با V=L³ بوده و جرم هریک از مولکول‌ها برابر با m است. هم‌چنین در نظر بگیرید که این جرم‌ها به صورت الاستیک به دیواره برخورد می‌کنند و دقیقا با سرعت برخورد، در جهت مخالف بر می‌گردند. در این صورت افزایش مومنتوم ناشی از برخورد برابر است با:

$$\triangle p=p_ {i\,x }−p _ { f\,x }=p_ {i\,x } −(−p_ { i\,x }) \\ =2p _ {i\,x } =2mv_ x$$

در رابطه فوق، v_x مولفه‌ی افقی سرعت قبل از برخورد به دیواره است. فرض بر این است که ذره در هر زمانِ $$\large \mathrm { Δ t = \frac { 2 L } { v _ x } }$$ یک برخورد با دیواره دارد. توجه داشته باشید که L برابر با فاصله دو دیواره‌ای است که روبروی هم قرار گرفته‌اند. با توجه به مفاهیم تکانه نیروی وارد شده در نتیجه‌ی این ضربه، برابر است با:

$$\large \mathrm { F = \dfrac { Δ p } { Δ t } = \dfrac { m v _ x ^ 2 } { L } }$$

با فرض این‌که N ذره در مخزن موجود باشد، نیروی وارد شده ناشی از کل آن‌ها برابر خواهد بود با:

$$\large \mathrm { F = \dfrac { N m \bar { v ^ 2 _ x } } L }$$

توجه داشته باشید که علامت بار قرار گرفته روی v، میانگین مقادیر روی تمامی ذره‌ها را نشان می‌دهد. بنابراین اگر جهات حرکت را به صورت ۳ جهتِ عمود بر هم در نظر بگیریم، میانگین اندازه برداری (جذرِ جمع توان دوم‌ در هر جهت) در هر سه جهت با هم برابر است. با توجه به این فرض سرعت x را می‌توان به صورت $$\large \mathrm { \bar { v _ x ^ 2 } = \frac { \bar { v ^ 2 } } { 3 } }$$ در نظر گرفت. بنابراین فشار وارد شده به سطح L² برابر است با:

$$\large \mathrm { P = \dfrac { F } { L ^ 2 } = \dfrac { N m \bar { v ^ 2 } } { 3 V } = \dfrac { n m \bar { v ^ 2 } } { 3 } \, }$$

در رابطه بالا حجم برابر با V=L³ است. هم‌چنین کسر $$\large n= \frac { N } { V }$$ نشان دهنده چگالی گاز است. رابطه بدست آمده در بالا اولین نتیجه نظریه جنبشی است. رابطه فوق ارتباطی بین انرژی جنبشی و خاصیتی مولکولی همچون فشار را برقرار می‌کند.

توزیع سرعت مولکول‌ها

در نظریه جنبشی گازها سرعت مولکول‌های یک گاز را می‌توان با استفاده از توزیع ماکسول-بولتزمن توصیف کرد. توجه داشته باشید که جهت و اندازه سرعت برای یک مولکول، عددی تصادفی است. با این حال، حرکت مجموعه ذرات یک گاز را می‌توان با استفاده از توزیع ماکسول-بولتزمن توصیف کرد. فرض کنید v_rms نشان دهنده میانگین سرعت کل مولکول‌ها باشد. نمودار زیر توزیع ماکسول-بولتزمن را برای حرکت مولکول‌ها در دو دمای مختلف نشان می‌دهد.

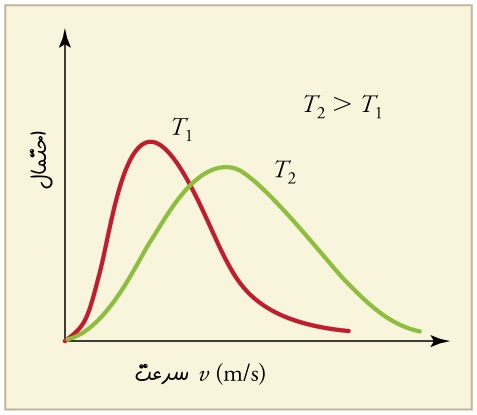
توجه داشته باشید که همواره بیشترین سرعت یا همان v_p کمتر از v_rms خواهد بود. البته در ادامه این توزیع را به صورت کمی توضیح خواهیم داد.

توزیع ماکسول-بولتزمن

توزیع ماکسول-بولتزمن توزیعی احتمالی است. این توزیع می‌تواند حرکت مولکول‌های یک گاز ایده‌آل قرار گرفته در شرایط تعادل ترمودینامیکی را توصیف کند. کمیتی تحت عنوان f_v یا تابع چگالی احتمال به صورت زیر بیان می‌شود.

$$\large \mathrm { f _ v ( v _ x \, v _ y \, v _ z ) = ( \dfrac { m } { 2 π k T } ) ^ { 3 / 2 } \exp ⁡[−dfrac { m ( v _ x ^ 2 + v _ y ^ 2+ v _ z ^ 2) } { 2 k T } ] }$$

تابع فوق نشان می‌دهد که میزان احتمال یافتن ذره‌ای در دیفرانسیلِ $$\large [ d v _ x \, d v _ y \, d v _ z ]$$ که در سرعت $$\large [ v _ x \, v _ y \, v _ z ]$$ قرار دارد، برابر است با:

$$\large \mathrm { f _ v ( v _ x \, v _ y \, v _ z ) d v _ x dv _ y d v _ z }$$

توزیع تنها در یک جهت به صورت زیر بیان می‌شود:

$$\large \mathrm { f _ v ( v _ i ) = \sqrt { \dfrac { m } { 2 π k T } } \; \exp ⁡[ \dfrac { − m v _ i ^ 2 } { 2 k T } ] }$$

هم‌چنین احتمال یافتن ذره‌ای با سرعت برداری $$[ v _ x \, v _ y \, v _ z ]$$ برابر با ضربِ احتمال آن‌ها در هریک از جهات است.

$$\large \mathrm { f _ v ( v _ x \, v _ y \, v _ z ) = f _ v ( v _ x ) f _ v ( v _ y ) f _ v ( v _ z ) }$$

توزیع سرعت

معمولا ما به بزرگی سرعت مولکو‌ل‌ها نسبت به جهتشان علاقه‌مند‌تر هستیم. توجه داشته باشید که سرعت هر ذره را می‌توان به صورت زیر بیان کرد:

$$\large \mathrm { v = \sqrt { v _ x ^ 2 + v _ y ^ 2 + v _ z ^ 2 } }$$

افزایش دیفرانسیل حجم در مختصات کروی را می‌توان به صورت زیر بیان کرد.

$$\large \mathrm { d v _ x \; d v _ y \; d v _ z = v ^ 2 \sin ⁡ϕ \; d v \; d θ \; d ϕ \, }$$

با انتگرال‌گیری از رابطه بالا به عبارت زیر می‌رسیم (باز‌ه‌های انتگرال به شکلی تعیین می‌شود که کل حجم یک کره را در بر بگیرد).

$$\large \mathrm { f ( v ) = \sqrt { ( \frac { m } { 2 π k T } ) ^ 3 } 4 π v ^ 2 \; \exp⁡ ( \frac { − m v ^ 2 }{ 2 k T } ) }$$

توزیع بدست آمده در بالا را توزیع ماکسول می‌نامند.

دما

در یک گاز ایده آل، دما به طور مستقیم وابسته به انرژی جنبشی انتقالی مولکول‌ها است. برای نمونه می‌توان گفت، میانگین سرعت حرکت مولکو‌ل‌ها در هوای داغ بیشتر است. در ادامه رابطه‌ای را مطرح خواهیم کرد که در آن ارتباط بین دمای گاز و میانگین انرژی جنبشی مولکول‌ها مشخص می‌شود.

دید میکروسکوپی

فرض کنید ابعاد یک مولکول نسبت به فاصله آن‌ها عددی کوچک است. هم‌چنین برهمکنش مولکول‌ها نسبت به یکدیگر را نادیده در نظر بگیرید. در این صورت می‌توان برخورد مولکول‌ها را با دیواره‌ محفظه به صورت کاملا الاستیک در نظر گرفت. در شکل زیر محفظه‌ای نشان داده شده که در آن جهت حرکت یک ذره نیز ترسیم شده است.

فیلم آموزش فیزیک 3 – حل تمرین در فرادرس

کلیک کنید

با توجه به شکل، جهت نیروی وارد شده به ذره در هنگام برخورد به سطح، فقط در راستای x است. با توجه به رابطه بدست آمده در بالا داریم:

$$\large \mathrm { P = \dfrac { N m \bar { v ^ 2 } } { 3 V } }$$

همان‌طور که پیش‌تر نیز بیان شد، در رابطه فوق P برابر با فشار، m نشان دهنده جرم و N تعداد کل مولکول‌ها را نشان می‌دهد. البته توجه داشته باشید که v و V به ترتیب نشان دهنده سرعت مولکول و حجم محفظه هستند.

البته رابطه فوق را می‌توان به صورت زیر نیز بیان کرد.

$$\large \mathrm { P V = \dfrac { 1 } { 3 } N m \bar { v ^ 2 } \; }$$

در رابطه بالا عبارت $$\large m \bar { v ^ 2 }$$ را می‌توان به صورت ضریبی خطی از انرژی جنبشی در نظر گرفت. بنابراین رابطه فوق به صورت زیر قابل بیان خواهد بود.

$$\large \mathrm { P V = N k T \; }$$

نهایتا از دو رابطه بالا، رابطه زیر بدست می‌آید.

$$\large \mathrm { \dfrac { 1 } { 3 } m \bar { v ^ 2 } = k T }$$

انرژی گرمایی

توجه داشته باشید که میانگین انرژی جنبشی یک مولکول در یک سیستم را می‌توان به صورت زیر بیان کرد:

$$\large \mathrm { \dfrac { 1 } { 3 } m \bar { v ^ 2 } = k T }$$

با توجه به روابط قسمت دید میکروسکوپی، انرژی جنبشی را می‌توان به صورت زیر بیان کرد:

$$\large \mathrm { \bar { K E } = \dfrac { 1 } { 2 } m \bar { v ^ 2 } = \dfrac { 3 } { 2 } k T }$$

توجه داشته باشید که به میانگین انرژی جنبشی مولکول‌ها، انرژی گرمایی نیز گفته می‌شود. با توجه رابطه بالا، سرعت میانگین مولکول‌ها را نیز می‌توان بر حسب انرژی گرمایی، به شکل زیر بدست آورد.

$$\large \mathrm { \bar { v ^ 2 } = v _ { r m s } = \sqrt { \dfrac { 3 k T } { m } } }$$

گاز‌های تک‌اتمی و چند اتمی

گاز تک اتمی به گازی گفته می‌شود که در آن پیوندی وجود ندارد. برای نمونه گاز‌های نجیب همچون هلیوم، آرگون و غیره، جزء گاز‌های نجیب محسوب می‌شوند.

در شکل زیر نمونه‌ای از کاربرد گاز نجیب را می‌توان دید. در حقیقت در کشتی‌های هوایی از گاز هیدروژن برای به پرواز در آوردن آن استفاده می‌کنند.

در گاز‌های نجیب، انرژی مولکول‌ها فقط انرژی جنبشی انتقالی را شامل می‌شود. در این گاز‌ها بدلیل مرتعش نبودن مولکول‌ها، می‌توان از انرژی دورانی و لختی دورانی مولکول‌ها صرف نظر کرد. در مورد گاز‌های تک‌اتمی نیز می‌توان رابطه زیر را بیان کرد.

$$\large \mathrm { U = \dfrac { 3 } { 2 } N k T }$$

با توجه به رابطه فوق کل انرژی داخلی گاز تک اتمی را نیز می‌توان به شکل زیر بیان کرد.

$$\large \mathrm { U = \dfrac { 3 } { 2 } N k T }$$

در رابطه بالا N برابر با تعداد اتم‌ها در گاز است. توجه داشته باشید که در گاز‌های تک‌اتمی سه درجه آزادی وجود دارد. در حقیقت هر اتم‌ می‌تواند در جهت y ،x یا z حرکت کند.

در گاز‌های چند اتمی هم‌چون $$\large O _ 2 \, H _ 2$$ هر مولکول علاوه بر حرکت در سه راستای اصلی، می‌تواند به دو صورت دوران نیز کند؛ بنابراین در این گاز‌ها درجه آزادی برابر با ۵ است. از این رو انرژی داخلی در گاز‌های چند اتمی برابر با $$\large \mathrm { U = \frac { 5 } { 2 } N k T }$$ در نظر گرفته می‌شود.

نکات کلیدی

• با استفاده از نظریه جنبشی گاز‌ها می‌توان به درک بهتری از تعریف فشار دست یافت.
• فشار که خاصیتی ماکروسکوپیک محسوب می‌شود را می‌توان با استفاده از انرژی جنبشی مولکول‌ها که خاصیتی میکروسکوپی هستند، معرفی کرد.
• از آنجایی که فرض بر این است که ذرات در جهات مختلف به صورت تصادفی حرکت می‌کنند، بنابراین می‌توان توان دوم سرعت‌ مولکول‌ها را در جهات مختلف، برابر و به صورت $$\large \mathrm { \bar { v _ x ^ 2 } = \bar { v _ y ^ 2 } = \bar { v _ z^ 2 } = \bar { v ^ 2 } / 3 }$$ در نظر گرفت.
• انرژی جنبشی انتقالی میانگین برای یک اتم را می‌توان برابر با $$\large \mathrm { \frac { 3 } { 2 } k T }$$ در نظر گرفته که معادل با انرژی حرارتی است.
• سرعت میانگین هر مولکول در یک گاز برابر با $$\large \mathrm { \sqrt { \frac { 3 k T } {m } } }$$ در نظر گرفته می‌شود.
• هر درجه آزادی معادل با $$\large \mathrm { \frac { 1 } { 2 } k T }$$ انرژی به ازای هر اتم است.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک و مهندسی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های مهندسی مکانیک
• مجموعه آموزش‌های فیزیک
• گاز ایده‌ آل — به زبان ساده
• معادله اویلر لاگرانژ — به زبان ساده
• طیف اتمی — از صفر تا صد