گاز کامل — از صفر تا صد
در علم شیمی و فیزیک، یک گاز کامل در حقیقت، مدلی از یک گاز نظری به شمار میآید که به کمک این مدل، محاسبات مربوط به گازها سادهتر خواهد شد. همچنین، نسبت به گاز ایدهآل، رفتار یک گاز کامل نیز سادهسازی میشود. مدل گاز کامل، نیروهای بین مولکولی را در نظر نمیگیرد و به همین دلیل، مباحث پیچیده مربوط به این مبحث، به هنگام بررسی گاز کامل در نظر گرفته نمیشوند.
مقدمه
در سطح ماکروسکوپی، برای توضیح فیزیکی نمونهای از یک گاز، به چهار کمیت زیر نیاز داریم:
متغیرهای بالا، هیچکدام متغیر مستقلی نیستند و اگر از این چهار متغیر، سه متغیر را داشته باشیم، میتوانیم متغیر چهارم را محاسبه کنیم و به این ترتیب، توصیفی فیزیکی از یک گاز داشته باشیم. حجم محفظه و تعداد ذرات گاز، مفاهیم مشخصی هستند اما برای درک گاز کامل باید توضیح مختصری از دما و فشار ارائه کنیم.
فشار
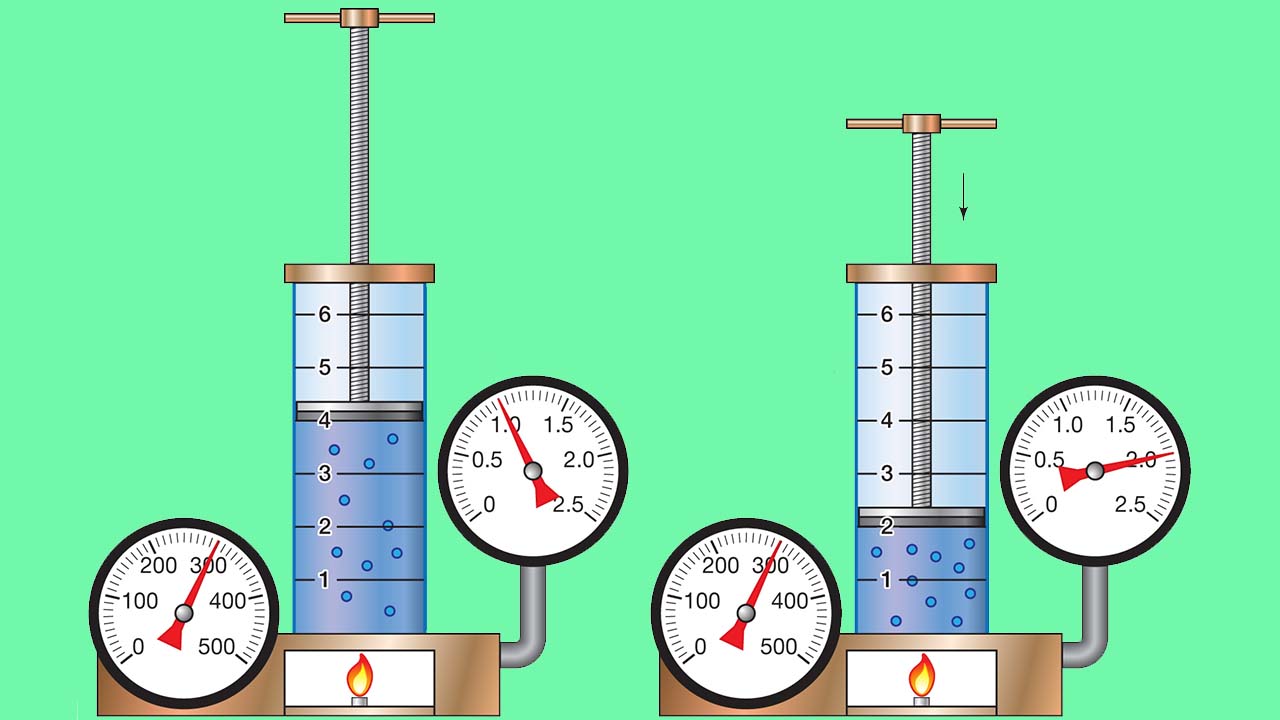
هر جسمی که با سطحی در تماس باشد، بر این سطح نیرویی وارد میکند. اگر سطح نیز به همان میزان، بر جسم نیرو وارد کند، جسم و سطح در تعادل مکانیکی قرار میگیرند. به طور مثال، هوای موجود در یک بالن، بر سطح داخلی بالن نیرو وارد میکند و این نیرو با مجموع نیروی هوای خارج و تنس کششی دیواره بالن برابر است. اگر هوای داخل بالن گرم شود، افزایش انرژی جنبشی گاز سبب انبساط آن میشود چرا که در نتیجه این کار، فشار گاز داخل بالن، افزایش پیدا کرده است. این فشار، برابر با نیرو به ازای واحد سطح بالن است که با رابطه زیر نشان داده میشود:
سطح/نیرو = فشار (P)
با توجه به رابطه بالا، فشار به نیروی اعمال شده و اندازه سطح بستگی دارد. با این تعریف در مییابیم که اعمال مقدار مشخصی نیرو بر سطحی کوچکتر، فشار بیشتری را نتیجه میدهد. واحد فشار، بر اساس واحدهای نیرو و سطح تعریف میشود. به طور مثال، واحد SI فشار از واحدهای SI نیرو و سطح بوجود میآید و برابر با نیوتون بر متر مربع ($$N / m ^ 2$$)، موسوم به پاسکال (Pa) است. تبدیل واحد فشار بین پاسکال و نیوتون بر متر مربع را در زیر مشاهده میکنید.
$$\rm 1\; P a = 1 \; N /m^2$$
فشار بارومتری
همانطور که به دلیل گرانش، بر روی سطح نیرو وارد میکنیم، اتمسفر (جو) نیز بر ما نیرو وارد میکند. در حقیقت، ما در اعماق اقیانوسی از گازهایی زندگی میکنیم که چگالی آنها با افزایش ارتفاع، کاهش پیدا میکنند. به طور تقریبی، حدود 99 درصد جرم اتمسفر، در 30 کیلومتری سطح زمین قرار دارد. هر نقطهای در سطح زمین، تحت فشاری موسوم به فشار بارومتری قرار دارد. فشاری که توسط اتمسفر اعمال میشود، مقدار قابل توجهی دارد. ستونی با سطح یک متر مربع که از سطح دریا تا بالای اتمسفر امتداد داشته باشد، جرمی برابر با 10000 کیلوگرم خواهد داشت که فشاری معادل 101 کیلوپاسکال ایجاد میکند.
فشار بارومتری را میتوان به کمک یک فشارسنج (بارومتر) اندازهگیری کرد. دستگاه بارومتر توسط یکی از شاگرادان گالیله به نام توریچلی اختراع شد. این دستگاه را میتوان به کمک لوله شیشهای بلند و سربسته تهیه کرد. این لوله شیشهای را با جیوه پر میکنیم و به صورت برعکس در ظرفی شامل جیوه قرار میدهیم به گونهای که هوایی به داخل آن وارد نشود. در اثر این اتفاق، مقداری جیوه از داخل لوله خارج میشود اما بخش زیادی از آن در داخل آن باقی میماند.
گرانش، نیرویی به سمت پایین در لوله ایجاد میکند اما هوای اتمسفر نیز، نیرویی بر جیوه داخل ظرف وارد خواهد کرد. در اثر این نیروی وارد شده، جیوه در داخل لوله به طرف بالا حرکت میکند. با توجه به اینکه هیچ هوایی در داخل لوله پرشده از جیوه وجود ندارد (شرایط خلا)، هیچ فشاری نیز به جیوه برای حرکت به پایین لوله وجود نخواهد داشت. در نتیجه، جیوه در لوله تا زمانی پایین میرود که فشار ستون جیوه با فشار اتمسفر برابر شود و میتوان گفت در این نقطه، فشار ستون جیوه در تعادل مکانیکی با فشار اتمسفر قرار دارد. فشار حاصل از ستون جیوه با رابطه زیر نشان داده میشود:
$$P =\dfrac {F} {A}= \dfrac {m g} {A} =\dfrac {\rho V\cdot g} {A} =\dfrac { \rho \cdot Ah\cdot g} {A} = \rho gh\; kPa$$
از بارومتر جیوهای بمنظور سنجش فشار بارومتری تا مدتها استفاده میشد که واحد آن میلیمتر جیوه (mmHg) بود و به طور معمول به دلیل نام توریچلی، «تور» (Torr) خوانده میشد. فشار استاندارد بارومتری، فشار مورد نیاز برای تامین ارتفاع ستون جیوه به میزان 760 میلیمتر جیوه ذکر میشود که معادل ۱ اتمسفر است. تمامی این واحدهای فشار، به صورت زیر با تبدیل واحد مناسب به واحد پاسکال مرتبط میشوند:
$$\rm 1\; a t m = 760 \; m m H g = 760 \; t o r r = 1.01325 \times 10^5 \; P a = 101.325 \; k Pa$$
فشار گاز
در بررسی یک گاز کامل باید به بیان مفهوم فشار اعمال شده توسط گاز هم پرداخت. یک بارومتر، فشار ستون مایع یا فشار بارومتری را اندازهگیری میکند اما برای سنجش فشار گاز محبوس، از مانومتر بهره میگیرند. ویژگی اصلی یک مانومتر، داشتن لولهای Uشکل حاوی جیوه است. این لوله Uشکل میتواند به صورت یکسر باز یا بسته باشد که این نوع از مانومترها در تصویر زیر نشان داده شدهاند.
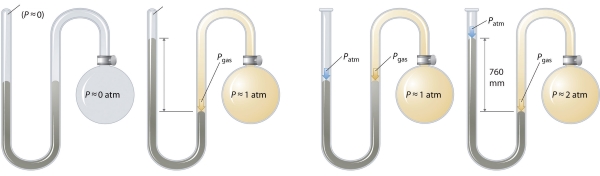
زمانیکه محفظه حبابی شامل هیچ گازی نباشد، ارتفاع دو ستون در لوله، یکسان است زیرا فضای بالای ستون جیوه در سمت چپ، برابر با خلا و تنها شامل مقادیر کمی از بخار جیوه است. اگر گاز موجود در محفظه حبابی آزاد شود، بر ستون جیوه سمت راست فشار اعمال میکند و در این حالت، دو طرف ستون با یکدیگر برابر نخواهند بود. فشار گاز، برابر با اختلاف ارتفاع ستون جیوه در دو طرف است.
اگر یک طرف مانومتر باز باشد، در اینصورت، تنها زمانی دو طرف ستون جیوه یک ارتفاع خواهند داشت که فشار محفظه حبابی، برابر با فشار بارومتری (فشار اتمسفر) باشد. اگر گاز داخل محفظه، فشار بیشتری داشته باشد، ستون سمت چپ، توسط این فشار اضافی بالا میرود. بنابراین، فشار گاز در محفظه، برابر با مجموع فشار بارومتری بعلاوه اختلاف ارتفاع دو ستون جیوه خواهد بود. اگر محفظه، فشاری کمتر از اتمسفر داشته باشد، اینبار، ارتفاع ستون جیوه در سمت راست بالاتر میرود و فشار گاز برابر با فشار بارومتر منهای اختلاف ارتفاع دو ستون است.
بارومتر و مانومتر، فشارسنجهای هیدرواستاتیک به شمار میآیند که در سنجش خود از ستون مایع کمک میگیرند. فشارسنجهای مکانیکی بدون مایع، به طور معمول از سطحی همچون لوله، سیم، دیافراگم یا نیمههادی بهره میگیرند که در اثر تغییر فشار، تغییر شکل میدهند.
دما
مفهوم دیگر در بررسی یک گاز کامل را باید به دما اختصاص داد. بسیاری از افراد، دما و گرما را با یکدیگر اشتباه میگیرند. دما معیاری برای سنجش میزان گرما یا سرمای یک جسم نسبت به جسمی دیگر است درحالیکه گرما (حرارت)، به جریان انرژی بین دو جسم با دمای متفاوت میگویند. سه مقیاس متفاوت برای اندازهگیری دما به نامهای فارنهایت (درجه)، سانتیگراد (درجه) و کلوین بکار میرود.
معادله حالت برای گاز کامل
یک معادله حالت، رابطهای است که متغیرهای مورد نیاز برای توصیف کامل حالت ماده را به یکدیگر مرتبط میکند. از نمونههای معادله حالت میتوان به رابطه $$V = f(p,T, n)$$ اشاره کرد که بیان میکند حجم یک نمونه از ماده، تابعی از فشار، دما و تعداد ذرات آن نمونه است. معادله دقیق برای یک گاز گامل یا قانون گاز کامل را در ادامه متن اثبات میکنیم.
طبق تعریف، گاز کامل به گازی میگویند که بین ذرات آن هیچ برهمکنشی وجود نداشته باشد. نمونهای از یک گاز که در آن، تمامی برهمکنشها یکسان باشند را با نام گاز ایدهآل میشناسند. بنابراین، یک گاز کامل را میتوان نوعی گاز ایدهآل دانست اما همه گازهای ایدهآل، گاز کامل نیستند.

اثبات قانون گاز کامل
رابطه بین کمیتی همچون حجم با سایر متغیرها (فشار، دما و تعداد ذرات) را به کمک ترکیب سه رابطه زیر و تبدیل آنها به یک رابطه بدست میآوریم. این معادله به طور همزمان، سه رابطه زیر را توصیف میکند.
قانون بویل: تناسب معکوس حجم با فشار در دما و تعدا ذرات ثابت
$$V \propto \dfrac{1}{P} \;\; \text{@ constant n and T}$$
قانون شارل: تناسب حجم با دما در فشار و تعداد ذرات ثابت
$$V \propto T \;\; \text{@ constant n and P}$$
اصل آووگادرو: تناسب حجم با تعداد ذرات در دما و فشار ثابت
$$V \propto n \;\; \text{@ constant T and P}$$
با ترکیب سه رابطه بالا، به رابطه زیر میرسیم:
$$V \propto \dfrac {n T} {P}$$
این رابطه نشان میدهد که حجم یک گاز به صورت مستقیم با دما و تعداد مولهای گاز و به صورت معکوس با فشار آن تناسب دارد. در نتیجه، با اضافه کردن یک ضریب به تناسب بالا، تناسب را به تساوی تبدیل میکنیم:
$$V = {\rm Cons.} \left ( \dfrac {n T } { P } \right)$$
به طور معمول، این ثابت تناسب، موسوم به ثابت جهانی گازها است که با R نشان داده میشود. با جایگذاری R، به رابطه زیر میرسیم.
$$V = \dfrac {n R T } {P} $$
برای حذف کسر، دو طرف معادله را در $$P$$ ضرب میکنیم.
$$P V = n R T$$
مقدار R را به کمک ضرب ثابت بولتزمن $$(N _ A)$$ در ثابت آووگادرو (k) بدست میآوریم.
$$R = N _ A k$$

استفاده از قانون گاز کامل
درصورتیکه سه متغیر از چهار متغیر مورد نیاز برای توصیف یک گاز کامل را داشته باشیم، محاسبه متغیر چهارم به کمک قانون گاز کامل بدست میآید. همچنین، به کمک این قانون، پیشبینی حالت نهایی یک نمونه گاز (دما، فشار، حجم و مقدار نهایی) به دنبال تغییر شرایط اولیه، امکانپذیر خواهد بود. برخی از کاربردهای قانون گاز کامل را در مثال زیر بررسی میکنیم. روش حل اینگونه سوالات همواره به اینصورت است که با نوشتن معادله گاز کامل شروع و مقادیر معلوم و مجهول را مشخص میکنیم. در مثالهای زیر، سه متغیر معلوم و یک متغیر مجهول داریم.
مثال بکارگیری قانون گاز کامل
بالنی به حجم 31150 لیتر داریم، اگر دما در سطح برابر با ۳۰ درجه سانتیگراد و فشار اتمسفری برابر با 745 میلیمتر جیوه باشد، چه تعداد مول گاز هیدروژن برای پر کردن بالون نیاز داریم.
برای حل این سوال، مراحل زیر را دنبال میکنیم:
- رابطه گاز کامل را برای متغیر مجهول، حل کنید.
- به واحد هر کمیت توجه داشته باشید و تبدیل واحد مناسب را برای جایگذاری در فرمول، بکار بگیرید.
مقادیر فشار، دما و حجم داده شده است و باید مقدار $$n$$ را محاسبه کنیم. با حل قانون گاز کامل برای $$n$$ خواهیم داشت:
$$n = \dfrac { P V } { R T }$$
واحدهای فشار و دما در این سوال باید به واحد مناسب در رابطه تبدیل شوند تا با واحد ثابت جهانی گازها مطابقت داشته باشند. در نتیجه، باید دما را به کلوین و فشار را به اتمسفر تبدیل کنیم.
$$T = 273+30 = 303 {\rm K}$$
$$\rm745\; m m H g \times \dfrac {1\;atm} {760\; m mH g }= 0.980\; a t m$$
با جایگذاری این دو رابطه در رابطه قبل برای $$n$$، تعداد مول هیدروژن مورد نیاز را بدست میآوریم:
$$n = \dfrac {P V } {R T } = \rm \dfrac {0.980\; atm \times 31150\; L } {0.08206 \dfrac {atm \cdot L} {\rm mol \cdot K}\times 303\; K } = 1.23$$
معادله عمومی گاز
زمانیکه یک نمونه گاز را در دو حالت مختلف بررسی میکنیم، باید در هر حالت به طور جداگانه، قانون گاز ایدهآل را در نظر بگیریم. در نتیجه، ۲ حالت اولیه (i) و نهایی (f) باید بررسی شوند. در هر حالت، ثابت جهانی گازها عدد مشخصی خواهد بود و در نتیجه، با حل رابطه گاز ایدهآل برای R و تساوی حالت اول و نهایی در رابطه بدست آمده، به معادله زیر میرسیم:
$$\dfrac {P _ i V _ i} {n_ i T _ i} = \dfrac { P _ f V_ f} {n_f T _ f }$$
رابطه بالا به معادله عمومی گاز یا «قانون ترکیبی گاز» (Combined Gas Law) معروف است. این رابطه زمانی کاربرد دارد که در دوحالت مختلف، یک یا دو خاصیت گاز، ثابت نگهداشته شوند، در چنین شرایطی، رابطه را با حذف مقادیر ثابت از دو طرف، ساده میکنیم.
مخلوط گاز کامل و قانون فشارهای جزئی دالتون
قانون گاز کامل فرض میکند که تمامی گازها، رفتاری مشابه دارند و این رفتار، مستقل از نیروهای جاذبه و دافعه است. اگر دما و حجم، ثابت نگه داشته شوند، معادله گاز کامل را میتوان به گونهای بازآرایی کرد که نشان دهد، فشار نمونهای از گاز به طور مستقیم با تعداد مولهای گاز موجود، مرتبط است:
$$P = n \left (\dfrac {R T } {V } \right ) = n \times \rm const.$$
با این شرایط، فرض میکنیم که مخلوطی از دو گاز کامل با مقادیر یکسان داشته باشیم. فشار کل این مخلوط، چه میزان خواهد بود؟ با توجه به اینکه فشار، تنها به تعداد کل ذرات گاز موجود بستگی دارد، فشار کل مخلوط گاز کامل به صورت ۲ برابر فشار هر جزء تعریف میشود. به طور کلی، فشار کل ناشی از مخلوط گازها در دما و حجم معلوم، برابر با مجموع فشارهای حاصل هرکدام از گازها است. علاوه بر این، اگر مقدار حجم، دما و تعداد مولهای هر گاز در مخلوط را داشته باشیم، میتوانیم فشار هر گاز را به طور مجزا محاسبه کنیم که با نام فشار جزئی شناخته میشود.
به طور خلاصه، فشار کل حاصل از مخلوط گازها برابر با مجموع فشارهای جزئی اجزای گاز است. این قانون در ابتدا توسط جان دالتون کشف شد. این قانون را با نام قانون فشارهای جزئی دالتون میشناسند که به صورت زیر نوشته میشود.
$$P _{tot} = P_1+ P_2+ P_3+ P_4 \; ... = \sum_ {i=1} ^ n {P_ i}$$
در رابطه بالا، $$P _{tot}$$ برابر با فشار کل و سایر عبارات، نشانگر فشارهای جزئی هستند.
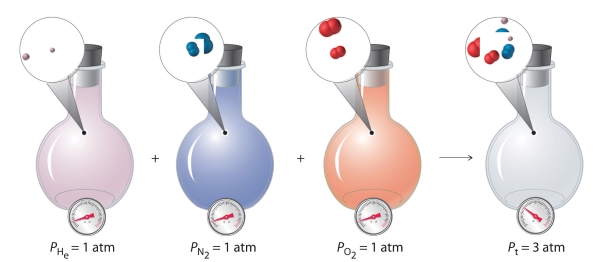
در مخلوط دو گاز کامل A و B، میتوان رابطهای را برای فشار کل مخلوط گاز کامل به صورت زیر نوشت:
$$P _ {tot} =P _A + P_B = n _ A \bigg (\dfrac {R T} { V } \bigg) + n _B \bigg (\dfrac {R T } {V} \bigg) = (n _A+ n_B) \bigg (\dfrac {R T } { V } \bigg )$$
در حالت کلی، برای مخلوطی با n جزء، فشار کل برابر است با:
$$P _ {tot} = ( P_1+ P_2+ P_3+ \; \cdots +P _n ) \bigg(\dfrac{ R T }{V }\bigg)$$
$$P _ {tot} = \sum _ {i=1} ^n {n _ i}\bigg(\dfrac{RT}{V}\bigg)$$
رابطه بالا، قانون فشارهای جزئی دالتون را به شکل عمومیتری نشان میدهد و به طور صریح بیان میکند که در دما و حجم ثابت، فشار حاصل از یک گاز، تنها به تعداد مول گاز موجود بستگی دارد، خواه این گاز، خالص یا مخلوطی از هزاران ذره مختلف باشد. در حقیقت، برای درستی رابطه بالا، ماهیت ذرات موجود نباید تاثیری داشته باشند.
بنابراین، یک گاز کامل به گازی میگویند که خواص آن متاثر از اندازه یا برهمکنشهای بین مولکولی نباشد چراکه این دو عامل، هر دو از یک گاز به گاز دیگر تغییر میکنند. در مثال زیر، محاسبات فشارهای جزئی و فشار کل را برای مخلوط گازها مورد بررسی قرار میدهیم.
مثال محاسبه فشار جزئی
غواصان آبهای عمیق باید به جای هوای فشرده، از کپسولی شامل مخلوطی از گازها استفاده کنند تا دچار بیماری «بندز» (Bends) یا تقلیل فشار ناگهانی نشوند. در عمق 350 فوتی از سطح دریا، فشاری معادل با 10 اتمسفر به این غواصها وارد میشود. کپسول گازی که در این عمق به طور معمول استفاده میشود، حاوی ۵۱/۲ گرم $$O _ 2$$ و 326/4 گرم هلیوم است و حجمی برابر با 10 لیتر دارد. فشار جزئی هر گاز در دمای ۲۰ درجه سانتیگراد را به همراه فشار کل کپسول در این دما حساب کنید.
برای حل این سوال، مراحل زیر را دنبال میکنیم:
تعداد مول هلیوم و گاز اکسیژن را محاسبه خواهیم کرد.
از قانون گاز کامل برای محاسبه فشار جزئی هر گاز بهره میگیریم. سپس این فشارهای جزئی را با یکدیگر جمع میکنیم تا فشار کل مخلوط گازی بدست بیاید.
تعداد مول هلیوم: $$n _ {\rm H e } = \rm \dfrac {326.4\;g} {4.003\;g /mol}= 81.54\; mol$$
تعداد مول گاز اکسیژن: $$n_ {\rm O_2}= \rm \dfrac {51.2\;g} {32.00\; g/ mol } =1.60\;mol$$
حال از قانون گاز کامل کمک میگیریم تا فشار جزئی هر گاز را محاسبه کنیم:
$$P _ {\rm He}=\dfrac {n _ {\rm He} R T }{V } = \rm \dfrac {81.54\;mol \times0.08206\;\dfrac {atm \cdot L } {mol \cdot K} \times293.15\;K } {10.0\;L} =196.2\;atm$$
$$P _ {\rm O _2} =\dfrac {n_ {\rm O_ 2} R T }{ V}= \rm \dfrac {1.60\;mol \times0.08206\;\dfrac {atm \cdot L} {mol \cdot K} \times 293.15\;K } {10.0\;L } = 3.85\;atm\
$$
در نهایت، برای بدست آوردن فشار کل، فشارهای جزئی بدست آمده را با یکدیگر جمع میکنیم.

کسر مولی مخلوط گازها
در بررسی یک گاز کامل باید کسر مولی مخلوط گازها را نیز مورد بررسی قرار دهیم. کسر مولی $$(X)$$ هر جزء از یک مخلوط، برابر با نسبت تعداد مولهای آن جزء به تعداد کل مولهای ذرات موجود در مخلوط $$(n _ {tot})$$ است که با رابطه زیر نشان داده میشود:
$$x _ A = \dfrac {\text {moles of A}} {\text {total moles}}= \dfrac {n _ A } {n_{tot}} = \dfrac {n _ A } {n_ A + n_ B+\cdots}$$
کسر مولی، کمیتی بدون است که مقداری بین ۰ تا ۱ دارد. اگر $$x_A = 1.0$$ باشد، نمونه خالصی حاوی ماده A داریم و اگر $$x_A = 0$$ باشد، هیچ مادهای از A در نمونه نخواهیم داشت. مجموع کسرهای مولی تمامی اجزا باید برابر با ۱ باشد.
برای اینکه فهم دقیقی از کسرهای مولی در بررسی خواص مخلوطهای گازی داشته باشیم، نسبت فشار گاز A را به فشار کل مخلوط گازی حاوی A میسنجیم. میتوانیم از قانون گاز کامل استفاده کنیم تا به توصیف فشار گاز A و فشار مخلوط بپردازیم.
$$P _ A = n _ A R T/ V$$
$$P _ {tot} = n_ t R T/ V$$
نسبت این دو مقدار برابر است با:
$$\dfrac {P _ A} {P_ {tot}} = \dfrac {n _ A R T / V} {n_{tot}RT/V} = \dfrac{n_A}{n_{tot}}=x_A$$
با بازآرایی رابطه بالا، به معادله زیر میرسیم:
$$P _ A = x _ A P _{tot}$$
این رابطه بیان میکند که فشار جزئی هر گاز در یک مخلوط، برابر با فشار کل ضربدر کسر مولی گاز است. این امر، نتیجه مستقیم قانون گاز کامل است که فرض میکند تمامی ذرات گازها، رفتاری ایدهآل دارند. در نتیجه، فشار یک گاز در مخلوط، تنها به درصد ذرات در مخلوط بستگی دارد و به خواص فیزیکی یا شیمیایی آن وابسته نیست.
به لحاظ حجمی، اتمسفر زمین شامل 78 درصد گاز نیتروژن، ۲۱ درصد گاز اکسیژن و 0/9 درصد گاز آرگون به همراه مقادیر کمی از گازهایی همچون دیاکسید کربن، بخار آب و ... است. این یعنی 78 درصد ذرات موجود در اتمسفر را گاز نیتروژن $$(N _ 2)$$ تشکیل میدهد.










چرا تو رابطه قانون گازهای ارمانی باید دما رو بر حسب کلوین جایگذاری کنیم حتی تو رابطه ی نسبیش؟
با سلام؛
برای اینکه دیمانسیون (ابعاد) این رابطه به طور صحیح نوشته شوند باید دما بر حسب کلوین نوشته شود. با دقت در ابعاد «ثابت جهانی گازها» نیز میتوانید این مورد را بررسی کرد. برای آشنایی بیشتر با این موضوع، مطالعه مطالب زیر پیشنهاد میشود.
ثابت جهانی گازها — از صفر تا صد
دیمانسیون — هر آنچه باید بدانید
با تشکر از همراهی شما با مجله فرادرس