مباحث کاربردی ریاضیات پایه برای علم داده

ریاضیات، پایه و اساس هر رشته علمی بخصوص در عصر حاضر است. جای تعجب نیست که تقریبا تمام تکنیک‌های «علم داده‌ مدرن» (Modern Data Science) بخصوص همه روش‌های «یادگیری ماشین» (Machine Learning) دارای برخی جنبه‌های عمیق ریاضیاتی هستند. در این مطلب، ما در مورد مباحث ریاضی ضروری در مقطع کارشناسی ارشد برای رشته علم داده می‌پردازیم که به نظر می‌رسد یک محقق پیشرو در علم داده باید از آن‌ها اطلاع داشته و یا حداقل با مفاهیم اولیه آن آشنا باشد.

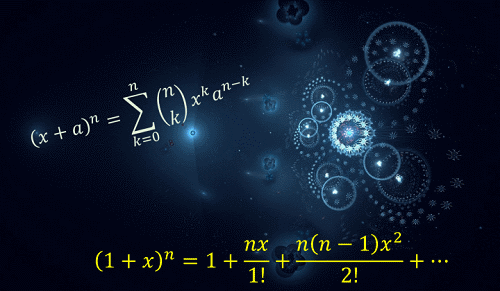
مقدمه

به عنوان یک «تحلیل‌گر داده» (Data Scientist) یا حتی به عنوان یک تحلیلگر جوان و تازه‌کار در تیم تحقیقاتی، باید از ریاضیات پایه آگاهی داشته باشید تا بتوانید از تکنیک‌های مربوط به روش‌های ریاضی به درستی استفاده کنید. در غیر این صورت بهتر است به فراگیری مباحثی که در ادامه معرفی خواهیم کرد بپردازید. البته بعد از این مرحله و فراگیری مباحث مربوطه، به راحتی به کمک الگوریتم‌ها و برنامه‌های آماده قادر به استفاده و تحلیل داده‌ها خواهید بود.

فیلم آموزش اف ایکس گراف – رسم نمودارهای ریاضی با FX Graph در فرادرس

کلیک کنید

درک درست از ریاضیاتی که در پشت چهره خشک و بی‌روح الگوریتم‌ها وجود دارد، نه تنها اتلاف وقت نیست بلکه شما را نسبت به نتیجه حاصل از تحلیل داده‌ها آگاه‌تر و قدرتمندتر می‌کند. در نتیجه بهتر می‌توانید محصول کار خود را به مشتریان ارائه دهید زیرا محصولتان پشتوانه قویی به نام ریاضیات دارد. به این ترتیب با اعتماد به نفس بیشتر نسبت به همکارانتان به فعالیت خواهید پرداخت. با فراگیری ریاضیات و مفاهیم آن، درست به مانند متخصص خودروی هستید که از همه فعالیت‌های آن آگاه است در حالیکه بدون دانش ریاضی تنها راننده‌ای خواهید بود که پشت فرمان نشسته و هیچ اطلاعاتی از نحوه کار خودرو ندارد.

بدون شک نیاز شما به همه جنبه‌های دانش وجود دارد، به کارگیری توانایی برنامه نویسی، آگاهی از وضیت بازار کسب و کار، تفکر تحلیلی و ذهنیت منحصر به فرد خود در مورد داده‌ها، همگی برای فعالیت در زمینه علم داده به کارتان خواهد آمد. ولی به هر حال، در اینجا به ریاضیات پایه‌ای اشاره خواهیم کرد که می‌تواند در رسیدن به مقامی مناسب در تحلیل داده‌ها به شما کمک شایانی کند.

اهمیت ریاضیات برای تازه‌کارها

آگاهی و شناخت از ریاضیات، پایه‌ای است برای حرفه‌ای شدن در زمینه‌های مختلف مانند مهندسین سخت‌افزار، عمده فروشی، فرآیندهای شیمیایی در صنعت، بهداشت و درمان، تجارت و... در نتیجه فراگیری آن بسیار اهمیت دارد. شاید به نظر برسد که انجام محاسبات ریاضی با استفاده از برنامه‌ها و «کاربرگ‌های الکترونیکی» (Spread Sheets)، به معنی استفاده از ریاضیات است. ولی به کارگیری ریاضیات، در علم داده، چیزی فراتر از حساب کردن بوسیله چهار عمل اصلی است.

چرا و چگونه اعداد با ریاضیات متفاوت است؟

پاسخ این است، ریاضیات علم است و به معنی داده نیست. یک برنامه نویس وب یا تحلیل‌گر بازار را در نظر بگیرید. هر کدام از این افراد، ممکن است در هر روز با داده‌ها و اطلاعات زیادی مواجه شوند و درگیر انجام محاسبات زیاد و پیچیده‌ای باشند. ولی هیچ یک از آن‌ها روی مدل‌سازی و درک الگویی که داده‌ها دارند متمرکز نیستند. البته محدودیت زمانی و احتیاج به آمار و ارقام سریع و به موقع ممکن است ذهن آن‌ها را از مدل‌سازی دور کند و اجازه تفکر عمیق در مورد رفتار داده‌ها را از آن‌ها بگیرید. ولی کاری که تحلیل‌گر داده انجام می‌دهد یک کار علمی است که در مسیر یک فرآیند صحیح اجرا می‌شود. از این جهت مراحل یک فرآیند علمی را می‌توان به صورت زیر طبقه‌بندی کرد:

• مدل‌سازی یک فرآیند (فیزیکی یا اطلاعاتی) با بررسی جنبه‌های پویای مسئله
• تشکیل فرضیات
• ارزیابی کیفیت منابع اطلاعاتی
• تعیین حدود اطمینان برای پیش‌بینی‌ها حاصل از داده‌ها
• شناسایی الگوهای پنهان موجود در داده‌‌ها
• تشخیص و تعیین محدودیت‌های مدل ارائه شده
• سعی در شناخت مراحل اثبات منطقی و ریاضی مسئله

چنین روشی به معنی استفاده از قدرت تحلیل و تفکر منطقی به جای به کارگیری از ابزارات محاسباتی است که باید در یک دوره چهارساله دانشگاهی آموزش داده شود. در اینجا منظورمان از ریاضیات، حساب دیفرانسیل و انتگرال نیست، بلکه ممکن است مسئله بسیار ساده‌تر باشد، مثل خود اعداد (مثلا ۲). فرض کنید در یک روزکاری پشت میزتان مشغول هستید. متوجه یک ای میل از رییس (یا دوست دانمشندتان) می‌شوید با موضوع: «در عرض ۲ دقیقه ثابت کن که ریشه ۲ عدد ۲ یک عدد گویا نیست.» این چه سوالی است؟ مگر اعداد گویا و ساکت هستند؟ از طرفی به نظر می‌رسد که عدد ۲ در عبارت بالا همیشه به یک معنی نیست. این سوال را چگونه باید درک کرد؟

راز موفقیت در چیست؟

مشکل در پیدا کردن راه صحیح و موفقیت‌آمیز است. متاسفانه برای همه مسائل نمی‌توان یک راه و روش ارائه داد. برای مثال عدد ۲ در متن بالا همیشه یه یک معنی نیست. به همین ترتیب نیز علم داده، براساس طبیعت و ماهیتش، در یک زمینه خاص به کار نمی‌رود و با پدیده‌های متنوع و زیادی درگیر است و تلاش می‌کند که آن‌ها را درک و مدلسازی کند. تنوع کار یک تحلیل‌گر داده از روش‌های تشخیص و درمان سرطان گرفته تا علوم اجتماعی و تحلیل رفتارهای فردی حتی در یک پروژه قابل تغییر و گسترده است. بنابراین چنین فردی با متغیرهای nبعدی با توزیع‌های آماری پیچیده، بهینه سازی توابع هدف و ... سر و کار خواهد داشت.

پس بهتر است این ابزارات ریاضی را بهتر بشناسیم.

تابع، متغیر، معادله و نمودار

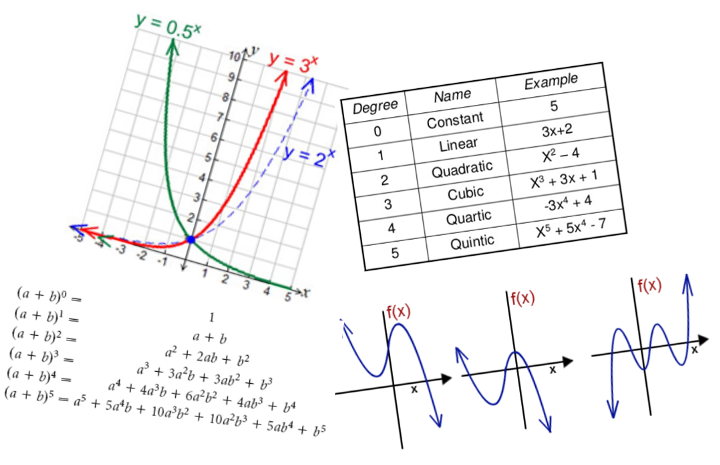
مفاهیمی مانند تابع، متغیر معادله و نمودار از ساده‌ترین مسائل (مانند تعیین معادله خط یا قضیه دو جمله‌ای) تا پیچیده‌ترین مباحث ریاضی به کار می‌روند. زمینه‌های که این مفاهیم در آن استفاده می‌شود را می‌توان در لیست زیر مشاهده کرد.

• توابع لگاریتمی، نمایی و چند جمله‌ای، اعداد گویا
• هندسه و قضیه‌های آن، مثلثات
• اعداد حقیقی و مختلط به همراه خصوصیات اصلی آن‌ها
• دنباله‌ها، مجموع آن‌ها و نامساوی‌ها
• ترسیمات و نمودارها، مختصات دکارتی و قطبی و مقاطع مخروطی

برای مثال اگر می‌خواهید علت اینکه یک جستجو در لیست مرتب شده از میلیون‌ها قلم کالا چگونه سریع‌تر از حالت بدون مرتب‌سازی است را دریابید، با مفهوم جستجوی دو دویی (Binary Search) برخورد خواهید کرد. اگر می‌خواهید سرعت آن جستجو را بسنجید باید از لگاریتم و معادلات برگشت‌پذیر مطلع باشید. یا اگر می‌خواهید یک تحلیل سری زمانی انجام دهید با مفاهیم مانند توابع تناوبی و یا نمایی نزولی مواجه خواهید شد.

آمار

اصلی‌ترین مبحثی که یک تحلیل‌گر داده باید بیاموزد، آمار است. آگاهی از اصول آمار و احتمال چیزی است که هرگز نمی‌توان از موارد ضروری یک تحلیل‌گر داده حذف کرد. بسیاری از مبتدیان که تازه به علم داده روی آورده‌اند، متوجه خواهند شد که یادگیری ماشین (به جز روش شبکه عصبی) همان مباحث مربوط به آمار و یادگیری آماری است.

فیلم آموزش مبانی جبر – حل تست كنكور ارشد در فرادرس

کلیک کنید

البته بحث در این زمینه و معرفی تکینک‌های آماری که در یادگیری ماشین کاربرد دارند، طولانی و زمان‌بر است به همین دلیل به معرفی چند مفهوم و تکنیک ضروری و اولیه آمار که در علم داده به کار گرفته می‌شود بسنده می‌کنیم.

• آمار توصیفی و شاخص‌های آماری، مانند شاخص‌های تمایل به مرکز (میانگین، میانه و نما) ،‌ واریانس و شاخص‌های پراکندگی، کوواریانس و ضریب همبستگی.
• احتمال و مفاهیم آن مانند، روش‌های شمارش، محاسبه احتمال، امید ریاضی، قضیه بیز و احتمال شرطی
• تابع توزیع احتمال، توزیع یکنواخت، نرمال، دو جمله‌ای، کای ۲، توزیع t و قضیه حد مرکزی
• نمونه‌گیری، مقیاس‌های اندازه‌گیری، خطا، تولید اعداد تصادفی
• آزمون فرض، فاصله اطمینان، مقدار احتمال
• تحلیل واریانس (ANOVA)، آزمون میانگین
• رگرسیون خطی، با قاعده سازی

در چه مواردی باید از این روش‌ها استفاده کرد؟ پاسخ ساده است. در مصاحبه‌های کاری. بله دقیقاً همینطور است. به عنوان یک تازه کار در حوزه کاری تحلیل داده، اگر به طور عمیق از مفاهیم گفته شده در بالا اطلاع داشته باشید، کاملا کسی که پشت میز نشسته و از شما سوال می‌پرسد را تحت تاثیر قرار داده و به سرعت او را وادار می‌کنید که شما را استخدام کند. بعد از این مرحله با استفاده از روش‌های آماری که فراگرفته‌اید می‌توانید وظایف و کارهای روزانه را به راحتی انجام دهید.

جبر خطی

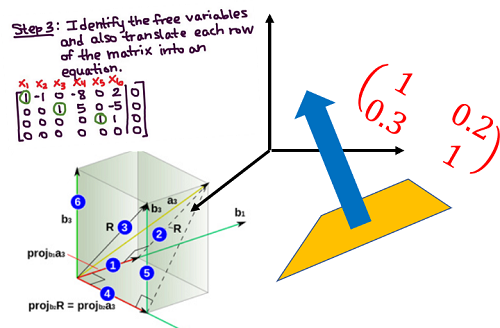
مثال‌های متعددی از محاسبات جبرخطی در علم داده، وجود دارد. پیشنهاد دوست جدید در «فیس‌بوک» (Face Book)، پیشنهاد موسیقی مورد علاقه‌تان در «اسپاتیفای» (Spotify)، تبدیل عکس سلفی شما به یک تابلو از «سالوادور دالی» (Salvador Dali) به کمک روش یادگیری عمیق و ... مثال‌هایی از استفاده از جبرخطی در علم داده محسوب می‌شوند. چیزی که در این مثال‌ها مشترک است وجود یک ماتریس و انجام محاسبات برمبنای آن است. جبرخطی شاخه‌ای از ریاضیات است که به درک عملیات و محاسبات صورت گرفته در یادگیری ماشین کمک می‌کند. الگوریتم‌های یادگیری ماشین به کمک جبر خطی قادر هستند که اطلاعات درون داده‌ها را استخراج کرده و به دانش تبدیل کننند. مباحث ضروری در این شاخه از ریاضیات در ادامه، فهرست شده‌اند.

• خصوصیات اصلی و محاسبات پایه روی بردارها و ماتریس‌ها، ضرب مقدار عددی در بردار و ماتریس، تبدیلات خطی، ترانهاده، مزدوج، رتبه و دترمینان
• ضرب داخلی و خارجی بردارها، قواعد ضرب ماتریس و الگوریتم‌های آن، ماتریس معکوس
• مفاهیم مربوط به تجزیه ماتریس، حل سیستم معادلات خطی
• فضای برداری، پایه، پوشش، تعامد،‌ کمترین مربعات خطی
• مقادیر ویژه، بردار ویژه و قطری سازی، تجزیه مقدارهای تکین (SVD)

برای مثال اگر می‌خواهید ابعاد یک مسئله با تعداد متغیرهای زیاد را کاهش دهید، تکنیک PCA یا تجزیه به مولفه‌های اصلی (Principal Component Analysis) که یک روش تجزیه مقدارهای تکین (SVD) است به کار می‌آید. در بیشتر الگوریتم‌های شبکه عصبی نیز روش‌های جبرخطی به منظور بیان یا پردازش ساختار شبکه و عملیات یادگیری به کار می‌روند.

حسابان

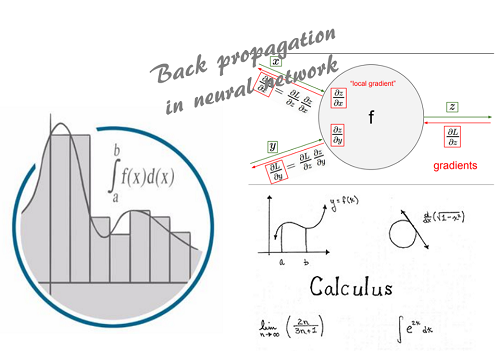
اگر چه ممکن است در دوره دانشگاه از حسابان (حساب دیفرانسیل و انتگرال) دل خوشی نداشته باشید، ولی به عنوان یک واقعیت سر و کله حسابان در بسیاری از رشته‌ها و زمینه‌های کاری علم داده یا یادگیری ماشین، پیدا خواهد شد. برای مثال روش پیدا کردن پارامترهای مدل در رگرسیون خطی ساده، استفاده از مشتق است که در حسابان آموخته می‌شود. همینطور در پس محاسبات شبکه عصبی هنگام یادگیری یک الگوی جدید، حسابان قرار دارد. به همین علت یادگیری حساب دیفرانسیل و انتگرال می‌تواند رشد شما به عنوان یک تحلیل‌گر داده را تسریع بخشد. در ادامه به سرفصل‌هایی از حسابان که می‌تواند برایتان مفید باشد می‌پردازیم.

• تابع یک متغیره، حد،‌ پیوستگی و مشتق‌پذیری
• قضیه مقدار میانگین، قاعده مقدار میانی
• نقاط اکستریمم (کمینه و بیشینه سازی تابع)
• قانون زنجیره‌ای مشتق
• سری تیلور، جمع دنباله‌ها
• قضیه اصلی حساب دیفرانسیل و انتگرال، محاسبه انتگرال معین و ناسره
• تابع توزیع بتا و گاما
• توابع چند متغیره، حد و پیوستگی آن‌ها، مشتقات جزئی
• اصول حل معادلات دیفرانسیل با مشتقات جزئی (مقدماتی)

به عنوان مثال می‌توان رگرسیون لجستیک اشاره کرد که در آن از مباحث حسابان استفاده می‌شود و در علم داده بخصوص یادگیری نظارت شده نیز کاربرد فراوان دارد. به عنوان کاربرد مشتق در علم داده می‌توان به الگوریتم گرادیان نزولی اشاره کرد که براساس کمینه‌سازی یک «تابع زیان» (Loss Function) عمل می‌کند. برای درک بهتر این الگوریتم باید با مفاهیم مشتق، گرادیان، حد و قاعده زتجیره‌ای مشتق آشنای داشته باشید.

ریاضیات گسسته

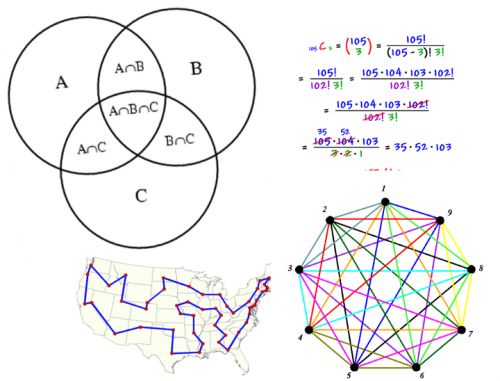
در بحث ریاضیات مربوط به علم داده، کمتر به ریاضیات گسسته اشاره شده است. ولی در حقیقت در علم داده مدرن، باید از محاسبات و ریاضیات گسسته در قلب سیستم‌های محاسباتی استفاده شود. به عنوان یک کارآموز علم داده، بهتر است با مبانی الگوریتم‌ها و ساختار داده‌ها آشنا باشید. برای معرفی مباحثی که در ریاضیات گسسته لازم به نظر می‌رسد لیستی تهیه شده که در ادامه می‌توانید ببینید.

• مجموعه، زیر مجموعه و مجموعه توانی
• توابع شمارشی، ترکیبیات و اصول شمارش
• روش‌های استنتاج و استنباط منطقی، مثال نقض
• مبانی ساختمان داده‌ها شامل: پشته، صف،‌ گراف، برداری، جدول‌های درهم سازی، درخت
• مفاهیم اولیه در نظریه گراف شامل: اجزای مرتبط، درجه گراف، بیشترین جریان/کمترین برش و رنگ‌آمیزی گراف
• روابط برگشتی و معادلات مربوطه
• رشد توابع و نماد $$O(n)$$

در بیشتر تحلیل‌های شبکه‌‌های اجتماعی، مباحث مربوط به ریاضیات گسسته بخصوص نظریه گراف به کار گرفته می‌شود. همچنین الگوریتم‌هایی که در نظریه گراف مطرح است می‌تواند ابزاری برای تجزیه و تحلیل این گونه شبکه‌ها باشد. از طرف دیگر آگاهی از پیچیدگی زمانی و محاسباتی الگوریتم‌ها به کمک ریاضیات گسسته امکان‌پذیر است تا بر این اساس بتوان سرعت و اندازه حافظه را براساس حجم داده ورودی برای اجرای الگوریتم‌ها مقایسه و محاسبه کرد.

بهینه‌سازی و مباحت تحقیق در عملیات

این موضوعات، به نظر بسیار به زمینه‌های تخصصی ریاضیات نظیر تئوری‌های علوم کامپیوتر، نظریه کنترل یا تحقیق در عملیات نزدیک است. ولی آگاهی از مفاهیم اولیه و آشنایی با تکنیک‌های قدرتمند آن‌ها، در شروع کار علم داده بخصوص یادگیری ماشین سودمند است.

فیلم آموزش نرم افزار Cabri 3D برای مدل سازی اشکال هندسی و هندسه فضایی در فرادرس

کلیک کنید

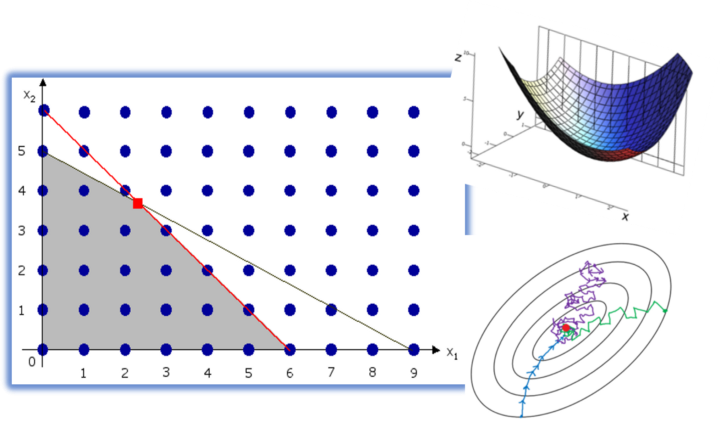
تقریبا همه الگوریتم‌های به کار رفته در روش‌های یادگیری ماشین، براساس «بهینه‌سازی» (Optimization) یک «تابع هدف» (Objective Function) کار می‌کنند که برحسب «تابع هزینه» (Cost Function) یا «تابع خطا» (Error Function) نوشته شده‌اند. پس در حقیقت در یادگیری ماشین،‌ با مسئله بهینه‌سازی مواجه هستیم. مواردی که در این زمینه‌ها بهتر است فرا گرفته شود در زیر فهرست شده‌اند.

• مفاهیم اولیه بهینه‌سازی،‌ فرموله کردن مسئله
• کمینه، بیشینه‌سازی توابع محدب، جواب‌های نسبی و مطلق
• برنامه‌ریزی خطی و الگوریتم سیمپلکس
• برنامه‌ریزی خطی عدد صحیح
• برنامه‌ریزی مقید و مسئله کوله‌پشتی
• روش بهینه‌سازی تصادفی و الگوریتم تپه نورد، الگوریتم تبرید شبیه‌سازی شده و الگوریتم ژنتیک

به عنوان مثال در بسیاری مواقع پاسخ‌های صریحی برای پارامترهای رگرسیون خطی ساده به روش کمترین مربعات خطا و یا رگرسیون لوجستیک وجود ندارد. در نتیجه استفاده از روش‌های بهینه‌سازی در چنین مواقعی ضرورری به نظر می‌رسد. مفهوم «تابع محدب (Convex Function) و بهینه‌سازی آن در این حالات کارساز است. به این ترتیب پاسخ‌های تقریبی برای مسائل یادگیری ماشین راه را برای تحلیل‌گر علم داده روشن می‌سازد. پس می‌توان نتیجه گرفت که آشنایی با این مباحث به زحمتش می‌ارزد.

نتیجه‌گیری نهایی

لیست‌های ارائه شده به نظر طولانی و مفصل هستند ولی باید توجه داشت که منابع یادگیری این مباحث به راحتی در اینترنت و در آموزش‌های فرادرس قابل مشاهده هستند. با صرف کمی زمان و حوصله با فراگیری یا حداقل آشنایی با مفاهیم گفته شده، درک شما را از مسائل تحلیلی که در یادگیری ماشین و علم داده با آن‌ها برخورد می‌کنید، بهبود می‌یابد و احتمالا ابزارهای متنوع و کارآمدی برای حل آن‌ها مسائل مختلف در اختیارتان قرار خواهد داد.

اگر به مباحث مرتبط به ریاضیات علاقه‌مند هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• گنجینه آموزش های محاسبات هوشمند
• گنجینه آموزش های بهینه سازی هوشمند و محاسبات تکاملی
• گنجینه آموزش های آمار و نرم افزارهای آماری
• آموزش خوشه بندی تفکیکی با نرم افزار R
• آموزش آمار و احتمال مهندسی
• آموزش آنالیز واریانس با SPSS
• خوشه بندی سلسله مراتبی (Hierarchical Clustering) — به همراه کدهای R
• ٰاعتبار سنجی متقابل (Cross Validation) — به زبان ساده
• رگرسیون را به سادگی و با مجموعه مقالات وبلاگ فرادرس یاد بگیرید

^^