ماتریس چیست؟ | ماتریس در ریاضی — به زبان ساده
در این مطلب از مجله فرادرس قصد داریم با مفهومی پرکاربرد تحت عنوان ماتریسها را توضیح دهیم. البته در آینده ضرب ماتریسها، ترانهاده ماتریس و معکوس ماتریسها را نیز توضیح خواهیم داد. ماتریس، آرایشی منظم از اعداد است که در سطر و ستونهای مشخصی مرتب شدهاند. برای مثال در تصویر زیر یک ماتریس با 2 سطر و 3 ستون مشاهده میکنید که ماتریس 3×2 نامیده میشود:
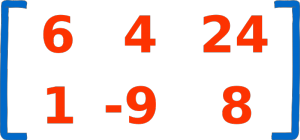
ماتریسها کاربردهای زیادی در محاسبات شاخههای مختلف دانش دارند و در واقع کارهای بسیاری را می شود با ماتریس ها انجام داد. برای نمونه میتوان با استفاده از آنها معادلات با درجه ۳، ۴ و بالاتر را تحلیل و پاسخهای آنها را بدست آورد. حتی میتوان معادله صفحه و یا خط را با استفاده از آرایش ماتریسی توصیف کرد. در تمامی شاخههای فیزیک، شامل مکانیک کلاسیک، نورشناسی، الکترومغناطیس، مکانیک کوانتوم و الکترودینامیک کوانتومی، ماتریس برای مطالعهی پدیدههای فیزیکی به کار میرود.
سطر ها و ستون های ماتریس
هر ماتریس از یک یا چند سطر و ستون تشکیل یافته است.
- سطر ها از چپ به راست هستند.
- ستون ها از بالا به پایین هستند.
باید توجه داشته باشید که در هر عملیاتی بر روی ماتریس، سطرها بر ستونها مقدم هستند.
دَرایه
ماتریس معمولا با یک حرف بزرگ انگلیسی (مانند A یا B) نمایش داده می شود. به هر یک از اعداد درون ماتریس یک عنصر یا درایه ماتریس گفته می شود. برای مشخص کردن هر درایه در ماتریس عدد ردیف و ستون آن را به ترتیب بصورت زیرنویس حرف کوچک نام ماتریس می نویسیم. برای نمونه اگر یک ماتریس A نام دارد، درایه ای که در سطر دوم و ستون سوم آن قرار دارد به صورت a23 مشخص میشود.
مثال:
ماتریس B برابر است با:
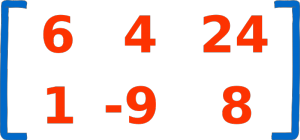
برخی از درایه های نمونه عبارتند از:
- b1,1 = 6 (درایه ماتریس در سطر 1 و ستون 1 برابر 6 است)
- b1,3 = 24 (درایه ماتریس در سطر 1 و ستون 3 برابر 24 است)
- b2,3 = 8 (درایه ماتریس در سطر 2 و ستون 3 برابر 8 است)
مرتبه ماتریس
به تعداد سطرها و ستونهای ماتریس که به صورت (ستون×سطر) نوشته میشود، مرتبه ماتریس می گوییم. برای مثال مرتبه ماتریس تصویر فوق 3×2 است و می گوییم این یک ماتریس 2 در 3 است. ماتریسی که تنها یک سطر داشته باشد، ماتریس سطری و ماتریسی که تنها یک ستون داشته باشد، ماتریس ستونی نامیده میشود. البته ماتریس تهی هم داریم، که ماتریسی است که هیچ درایهای ندارد. به ماتریسی که تعداد سطر ها و ستونهایش برابر باشند ماتریس مربعی گفته می شود.

عملیات ماتریسها
در ادامه به انواع مختلف عملیات ریاضی در مورد ماتریسها می پردازیم.
جمع ماتریسها
برای جمع دو ماتریس، اعداد هم مرتبه آنها را با هم جمع کنید:
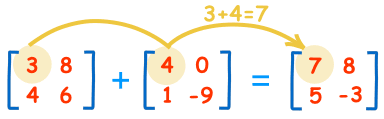
محاسبات به حالت زیر است:
3+4=7 8+0=8
4+1=5 6-9=-3
دو ماتریس برای جمع شدن باید هممرتبه باشند، یعنی باید تعداد سطرها و همچنین تعداد ستون های دو ماتریس با هم برابر باشند.
مثال: یک ماتریس با 3 سطر و 5 ستون می تواند با یک ماتریس دیگر که 3 سطر و 5 ستون دارد جمع شود؛ اما این ماتریس نمی تواند با یک ماتریس که 3 سطر و 4 ستون دارد جمع شود؛ چون اندازه ستون ها برابر نیست.
منفی کردن ماتریس
به دست آوردن منفی یک ماتریس کار سادهای است:
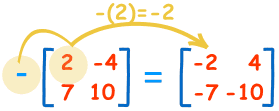
:محاسبات به نحو زیر است
-(2) = -2 -(-4) = +4
-(7) = -7 -(10) = -10
تفریق ماتریسها
:برای تفریق دو ماتریس می بایست اعداد هم مرتبه ماتریس ها را از هم تفریق کنید
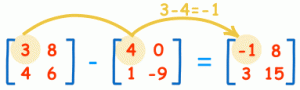
:محاسبات به نحو زیر است
3-4 = -1 8-0 = 8
4-1 = 3 6-(-9) = 15
در واقع عمل تفریق ماتریس به صورت جمع کردن ماتریس با منفی یک ماتریس دیگر تعریف میشود، یعنی A + (−B).
ضرب عدد ثابت در ماتریس
ما می توانیم یک عدد ثابت را در ماتریس ضرب کنیم. در مثال زیر عدد 2 در یک ماتریس ضرب شده است:
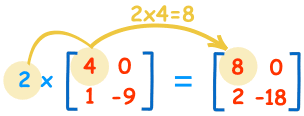
:محاسبات به نحو زیر است
2 × 4 = 8 2 × 0 = 0
2 × 1 = 2 2 × -9 = -18
این مضرب ثابت «اسکالر» (Scalar) نام دارد و این روش ضرب نیز اصولاً به نام «ضرب اسکالر» یا «ضرب نرده ای» نامیده میشود.
ضرب یک ماتریس در ماتریس دیگر
با توجه به این که عمل ضرب دو ماتریس در هم کمی متفاوت است، شما می توانید نوشته ضرب ماتریس ها را مطالعه کنید تا روش ضرب دو ماتریس در هم را یاد بگیرید.

تقسیم
در مورد تقسیم ماتریسها باید بگوییم که ما در واقع ماتریس ها را تقسیم نمی کنیم؛ بلکه به جای تقسیم، از روش زیر استفاده میکنیم:
A / B = A × (1 / B) = A × B -1
در عبارت فوق منظور از B -1، «معکوس ماتریس» B است. پس در واقع ما ماتریس ها را تقسیم نمیکنیم و به جای آن، ماتریس را در معکوس ماتریس دیگر ضرب میکنیم. اما معکوس ماتریس چیست و چگونه میتوان آن را محاسبه کرد. برای اطلاعات بیشتر در مورد معکوس یک ماتریس می توانید به نوشته «معکوس ماتریسها – به زبان ساده» مراجع کنید.
ترانهاده ماتریس
برای یافتن «ترانهاده» (Transpose) یک ماتریس، جای سطر ها و ستون ها را عوض کنید. از حرف " T " در سمت بالا و راست ماتریس، به عنوان نماد ترانهاده استفاده میضود.
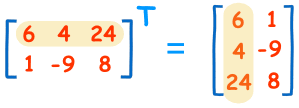













سلام ، من هنوز یک چیزی رو متوجه نشدم ، مگر یک مرتب مختصه یک نقطه رو در دستگاه مختصات به ما نشون نمیده؟! خب ماتریس در دستگاه مختصات (مثلا ماتریس 3×3) چی رو بما نشون میده ؟ اگه برداره نمایشش به چه صورته درک نمیکنم
سلام.مرسی از آموزش خوبتون.چطوری میشه با استفاده از ضرب ماتریس،جای بردار رو عوض کرد؟
سلام وقت بخیر
من یک کتاب به زبان ساده از ماتریس میخوام که راحت تر بتونم بفهمم.
تو سایت مطالب پخشه
کاش یه کتابی معرفی کنید که pdfش رو دانلود کنم.
من خارج از کشور هستم و درسی در مورد ماتریس دارم.ولی مطالب استاد رو به زبان انگلیسی متوجه نمیشم.
به نظرتون چیکار کنم؟
به روش وزبان سادهبود مناستفادهکردم
سلام فرادرس. یک سوال داشتم. عدد به توان ماتریس چطور حساب می شود. مثلا عدد 2 به توان ماتریس [4 2:3 1]؟
2 1
4 3
2
ممنون از آموزش روان و عالیتون.
در متن توضیح داده شده در قسمت تفریق ماتریسها، چرا
۱۵=(۹-)-۶
؟
یا درود و سپاس از مطالب مفید شما
فقط خواستم یاد آوری کنم که کلمه عمل یک کلمه عربی هست و جمع آن عملیات است. بنابراین دیگر نیازی به اضافه کردن “ها” بعنوان نشان ندارد.
سلام، وقت شما بخیر؛
از تذکر به جای شما بسیار سپاسگزاریم، مطلب بر همین اساس مورد بازبینی و اصلاح قرار گرفت.
از همراهی شما با مجله فرادرس و ارائه بازخورد ممنونیم.
چون منفی در منفی میشه مثبت و میشه 6 به علاوه 9 که میشه 15
سلام
یه سوال داشتم
با فرض ماتریس [A=[a1 a2 a3 a4 a5 و
ماتریس [B=[b1 b2 b3 b4 b5
در یک نرم افزار مثل متلب چگونه میتونم ماتریس
[c=[ a1*b1*a2*b2*…*a5*b5 * را محاسبه کنم؟
ممنون
واقعا عالی. سپاس از سایتتان که قطب اصلی آموزشی دانش است.
بسیار ممنون از آموزش خوبتون
عالی بود ممنون.
سلام وقت بخیر، a=b*c ماتریس aوb را داریم، a ستونی 1*3 هست و b 3*3 هست ، ماتریس c را چگونه باید بدست آورد؟
سلام. با توجه به رابطه A3×1=B3×3C3×1، ماتریس C ستونی و ۳ در ۱ است. برای به دست آوردن C، معموس ماتریس B را از چپ در دو طرف تساوی ضرب میکنیم. بنابراین، B−1A=B−1BC. از آنجا که B−1B=I، ماتریس C برابر خواهد بود با C=B−1A.
خوشحالیم که همراه مجله فرادرس هستید.
سلام اگه ماتریسی به نامAداشته باشیم ماتریس Aبه توان دوچطوری محاسبه میشه
به راحتی
سلام و با تشکر از همراهی شما با فرادرس!
منظور از توان دوم یک ماتریس، ضرب ماتریس در خودش است. البته به شرطی که ماتریس مربعی باشد، میتوان این کار را صورت داد. ولی اگر ماتریس nxn نباشد معمولا برای محاسبه مربع ماتریس A نتیجه حاصل ضرب ماتریس در ترانهاده آن در نظر گرفته خواهد شد.
باز هم از اینکه به نوشتههای مجله فرادرس توجه دارید سپاسگزاریم.
بسیار عالی و جامع
با سلام به تمامی دست اندرکاران سایت پر محتوا و مفید فرادرس من مدتی است که از آموزشها و مقالات شما استفاده میکنم ناسپاسی و دور از انصاف است که بخاطر تلاش اثرگذار شما مراتب قدردانی و تشکر خودم را اعلام ننمایم
عالی بود
بسیار علی بود ممنون از زحمتتون
مطالب سایت خیلی زیاد ساده و مفید….تشکرات فراوان
وبلاگتون عالیه. ولی هنوز جای کار داره. مثلاً میتونین برای هر مطلب، یه بخش جدید به عنوان نمونه سوالات اضافه کنین.
ضمن تشکر از مطالب ارزشمندتان احتمالا دو جمله اول نیاز به اصلاح دارند و جای سطر و ستون بایست تعویض گردد:
سطر ها از چپ به راست هستند.
ستون ها از بالا به پایین هستند.
سلام
دو ماتریس دارم به ابعاد 8×8 و 8×2 که میخوام باهم جمعشون کنم . ولی هر کاری میکنم error میده . میشه لطفا یه پیشنهاد بدید که چیکار کنم.
تشکر …
با درود و سپاس از اینکه همراه فرادرس هستید.
متاسفانه برای جمع دو ماتریس باید آنها دارای تعداد سطر و ستونهای یکسانی باشند. بنابراین جمع دو ماتریس ۸×۸ با ۸×۲ امکان پذیر نیست. بعضی از نرمافزارهای محاسباتی مانند پایتون با تکرار مولفههای ماتریس کوچکتر آن را هم اندازه با ماتریس بزرگتر کرده تا قابل جمع باشند. ولی در بقیه مواقع ممکن است انجام این کار در نرمافزارهای محاسباتی دیگر با پیغام خطا همراه باشد.
موفق و سربلند باشید.
توضیحات و نحوه تدریس در این سایت عالی هستش،بخصوص تدریسهایی که توسط خانم مریم دانیالی ارائه شدند،از ایشون و تمام مدرسان این سایت متشکرم?
سلام اگر ممکنه در مورد بدست آوردن ماتریس همنهشت و ماتریس متشابه آموزش ارائه کنید ممنون
ممنون عالی بود
یعنی واقعا ممنونم خیلی خوب بود معلم هرچی میگفت نمیفهمیدم ولی خدایی با مطالعه سایت شما مبحث ماتریس هارو در عرض ۵ دقیقه کامل فهمیدم همشو خیلی قشنگ و ب زبان ساده بیان کردین همه قسمت هارو واقعا ممنونم
به زبانی ساده سلیس و روان
درود بر شما
سلام خيلي ممنون از زحماتتون .ولي چرا در مورد ضرب ماتريس ها مطلب نگذاشته بودين ؟؟؟؟در حقيقت اشكال من در مورد ضرب ماتريس ها بود كه رفع نشد .
به دلیل اهمیت مبحث ضرب ماتریسها، این موضوع در نوشته جداگانهای تنظیم شده است که می توانید در اینجا بخوانید.
عالیه، عالی اموزش سریع و جذاب این سایت قابل تقدیره ممنونم واقعا
سلام عالی بود مشکلاتم حل شد ممنون از سایت خوبتون
سلام خسته نبااشید.عالی بود.سپاسگذارم ……
اگر میشه واسه من یکی توضیح بده که چرا ماتریس تقسیم نمیشه ؟ممنونم
عالی بود…با بیانی ساده و قابل فهم توضیح دادید…
سرکار خانم مریم دانیالی و مسئولین محترم سایت وزین فرادرس عالی بود. مشکلی در مورد ماتریسها داشتم که با توضیحات سایت شما کاملا مشکلم حل شد. همواره موفق باشید
با سلام
چطور دو ماتریس غیر هم سطح مثلا ۲در۲ را منهای ماتریس ۱ در ۱ کنیم؟
سلام.
دو ماتریس را تنها زمانی میتوانیم جمع یا تفریق کنیم که ابعاد یکسانی داشته باشند.
موفق باشید.
از توضیحات ساده و عالی شما سپاسگذارم
درود بر شما که در جهت علم آموزی رایگان قدم برمیدارید و درود بر آن هایی که با یادگرفتن این مطالب از زحماتتان سپاسگزاری میکنند 🙂