الگوها و دنباله های متداول عددی — به زبان ساده

اعداد در ریاضیات میتوانند الگوهای جالبی داشته باشند. این الگوها، شامل دنبالههای حسابی، هندسی، فیبوناچی و اعداد مثلثی هستند. در این مطلب از مجله فرادرس ما الگوها و دنباله های متداول عددی و نحوه تشکیل آنها را مورد بررسی قرار میدهیم. حاصل جمع یک دنباله یک سری را تشکیل میدهد که میتواند همگرا یا واگرا باشد.
دنبالههای حسابی
یک «دنباله (تصاعد) حسابی (عددی)» (Arithmetic Sequence) از جمع عددی ثابت در هر مرحله بهدست میآید. این عدد ثابت میتواند از مجموعه اعداد حقیقی انتخاب شود. در ادامه به حل چند مثال از این نوع دنباله های متداول عددی میپردازیم.
مثال ۱
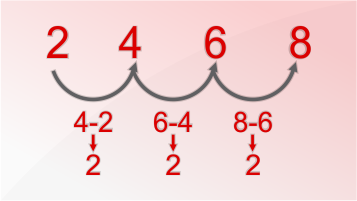
$$ 1, 4, 7, 10, 13, 16, 19, 22, 25, ... $$
در این دنباله، اختلاف هر دو عدد متوالی برابر با ۳ است. در واقع هر عدد این دنباله به اندازه ۳ واحد از عدد قبلی خود بیشتر و به اندازه ۳ واحد از عدد بعدی خود کمتر است.
این الگو با اضافه کردن 3، هر بار به آخرین عدد دنباله ادامه مییابد. این موضوع در شکل زیر به تصویر کشیده شده است.
مثال 2
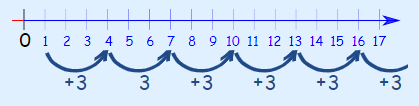
3, 8, 13, 18, 23, 28, 33, 38, ...
در این دنباله، اعداد نسبت به هم 5 عدد اختلاف دارند.
این الگو با اضافه کردن عدد 5، هر بار به آخرین عدد دنباله ادامه مییابد. این الگو در شکل زیر به خوبی نشان داده شده است.
مقدار اضافه شده در هر مرحله را «قدر نسبت« (Common Difference) مینامند. این مقدار، قدر نسبت حسابی نیز نامیده میشود.
برای مثال، قدر نسبت در مجموعه اعداد زیر چند است؟
19, 27, 35, 43, ...
این بار پاسخ را شما بگویید!
توجه کنید که قدر نسبت میتواند منفی باشد. مثال زیر به بیان این موضوع پرداخته است.
مثال 3
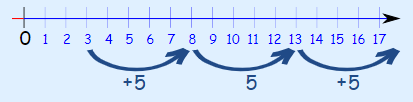
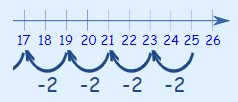
25, 23, 21, 19, 17, 15, ...
همانطور که مشاهده میشود، در این مثال قدر نسبت برابر با 2- است.
این الگو همچنان با تفریق 2 در هر مرحله از آخرین عدد دنباله ادامه مییابد، مانند:
برای تمرین، دنباله حسابی بنویسید که از 1 شروع شود و قدر نسبت آن برابر با قدر مطلق قدر نسبت مثال 3 باشد (توجه شود که قدر مطلق عدد 2- برابر 2 است). مشاهده میشود که دنباله حسابی شما، دقیقا معکوس مثال ۳ است.
دنبالههای هندسی
یکی دیگر از دنباله های متداول عددی، دنباله هندسی است که آن را تصاعد هندسی نیز مینامند. یک دنباله هندسی با ضرب یک عدد در هر مرحله تشکیل میشود. این موضوع در مثال زیر به صورت کامل بررسی شده است.
مثال 1
1, 3, 9, 27, 81, 243, ...
با دقت به دنباله بالا متوجه میشویم که این دنباله، یک ضریب 3 بین هر دو عدد متوالی خود دارد. در واقع اگر هر عدد این دنباله را در ۳ ضرب کنیم، عدد بعدی بهدست میآید. این موضوع در شکل زیر به خوبی نشان داده شده است.
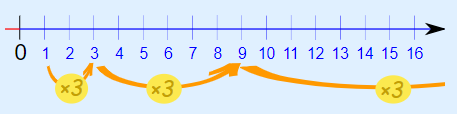
عددی که در هر مرحله ضرب میکنیم، قدر نسبت یا قدر نسبت هندسی نامیده میشود.
در مثال قبلی، قدر نسبت هندسی برابر با 3 بود.
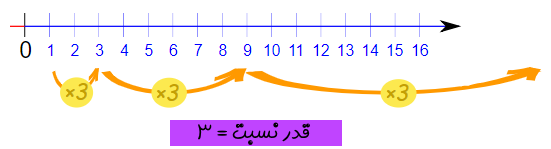
توجه شود که برای نوشتن یک تصاعد هندسی، میتوانیم با هر عدد دلخواهی، دنباله را شروع کنیم:
مثال 2
تصاعد هندسی بنویسید که قدر نسبت آن 3 است و با عدد ۲ شروع میشود.
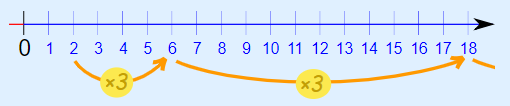
2, 6, 18, 54, 162, 486, ...
قدر نسبت این دنباله، مانند مثال قبل، مقداری برابر با 3 دارد، اما این بار، این دنباله با 2 شروع شده است.
مثال 3
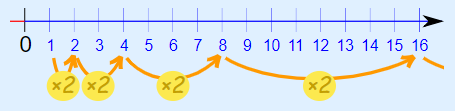
1, 2, 4, 8, 16, 32, 64, 128, 256, ...
این دنباله با عدد 1 شروع میشود و دارای قدر نسبت 2 است. هر مرحله از این دنباله، با ضرب مرحله قبل در عدد ۲ بهدست میآید. این موضوع در شکل زیر نشان داده شده است.
توجه شود که قدر نسبت میتواند کمتر از 1 نیز باشد. مثال زیر به بررسی این موضوع میپردازد.
مثال 4
10, 5, 2.5, 1.25, 0.625, 0.3125, ...
این دنباله با 10 شروع شده و قدر نسبت آن برابر با 0.5 است.
این الگو با ضرب اعداد در 0.5 در هر مرحله ادامه مییابد. در واقع هر عدد در این الگو، با ضرب عدد قبلی در 0.5 بهدست میآید.
نکته بسیار مهمی که باید به آن توجه کرد این است که قدر نسبت نمیتواند برابر با صفر باشد. در صورت صفر بودن قدر نسبت هندسی، دنبالهای مانند دنباله زیر خواهیم داشت!
1, 0, 0, 0, 0, 0, ...
دنبالههای ویژه
علاوه بر دنبالههای هندسی و حسابی که در قسمتهای قبل بیان شدند، دنباله های متداول عددی جذاب و کاربردی دیگری نیز در ریاضیات موجود هستند.
این بخش به بررسی این دنبالهها میپردازد.
دنباله اعداد مثلثی
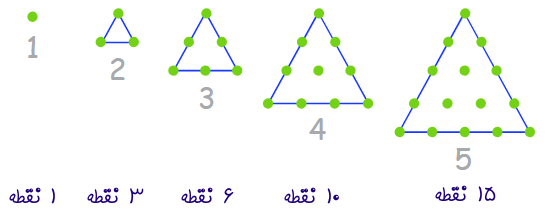
1, 3, 6, 10, 15, 21, 28, 36, 45, ...
دنباله مثلثی اعداد، با استفاده از الگوی نقاطی تشکیل میشود که یک مثلث را تشکیل میدهند. در هر مرحله از این دنباله، یک ردیف به نقاط مثلث اضافه میشود و با شمارش تعداد نقاط مثلث جدید، میتوانیم عدد بعدی دنباله را بهدست بیاوریم. شکل زیر به بررسی شیوه محاسبه این دنباله میپردازد.
اعداد مربع
0, 1, 4, 9, 16, 25, 36, 49, 64, 81, ...
اعداد دنباله بالا، مربع اعداد صحیح را نمایش میدهند و به آن الگوی مربعی میگویند. روابط زیر به بررسی شیوه محاسبه دنباله بالا میپردازند.
0 -> ( = 0 × 0 )
1 -> ( = 1 × 1 )
4 -> ( = 2 × 2 )
9 -> ( = 3 × 3 )
16 -> ( = 4 × 4 )
و ...
اعداد مکعب
1, 8, 27, 64, 125, 216, 343, 512, 729, ...
این دنباله اعداد، مکعب تمامی اعداد طبیعی را نشان میدهد (توجه شود که اعداد طبیعی از یک شروع میشوند).
1 -> ( = 1 × 1 × 1)
8 -> ( = 2 × 2 × 2)
27 -> ( = 3 × 3 × 3)
64 -> ( = 4 × 4 × 4)
و ...
اعداد فیبوناچی
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
دنباله فیبوناچی با جمع دو عدد پیشین در هر مرحله بهدست میآید. برای مثال، عدد 2 با جمع دو عدد پیشین خود محاسبه شده (1 + 1 = 2) و عدد 21 این دنباله با جمع دو عدد پیشین خود بهدست آمده است (13 + 8 = 21).
عدد بعدی این دنباله یعنی عدد بعد از 34 برابر با 55 خواهد بود (34 + 21 = 55).
می توانید اعداد بعدی را نیز حساب کنید؟
آزمون سنجش یادگیری دنباله های متداول عددی
در این بخش از مجله فرادرس، سطح اطلاعات شما در مبحث دنباله های متداول عددی را با طرح سوالهای چندگزینهای میسنجیم. پس از جواب دادن به تمام سوالها، نتیجه آزمون برای شما به نمایش درمیآید.
اگر اولین عدد مربعی مثبت برابر با 1 باشد ($$ 1 ^ 2 = 1 \times 1 = 1 $$)، دهمین عدد مربعی مثبت چه خواهد بود؟
20
81
100
1000
بر اساس توضیحات صورت سوال، دهمین عدد مربعی با استفاده از رابطه زیر به دست میآید:
$$ 10 ^ 2 = 10 \times = 100 $$
بنابراین، این عدد برابر با 100 است.
اگر اولین عدد مکعبی برابر با 1 باشد ($$ 1 ^ 3 = 1 \times 2 \times 1 = 1 $$)، دهمین عدد مکعبی چند خواهد بود؟
300
1000
3000
10000
با توجه به اطلاعات سوال، دهمین عدد مکعبی برابر است با:
$$ 10 ^ 3 = 10 \times 10 \times 10 = 1000 $$
بنابراین، دهمین عدد مکعبی برابر با 1000 است.
عدد بعدی در دنباله $$ 1,3,7,15,31,... $$ چیست؟
47
48
62
63
دنباله $$ 1,3,7,15,31,... $$، از یک قانون ساده پیروی میکند. این قانون، «دو برابر کردن عدد قبلی و جمع آن با عدد 1» است:
$$
\begin{aligned}
& 2 \times 1+1=2+1=3 \\
& 2 \times 3+1=6+1=7 \\
& 2 \times 7+1=14+1=15 \\
& 2 \times 15+1=30+1=31
\end{aligned}
$$
بر اساس قانون دنباله بالا، عدد بعدی عبارت است از:
$$ 2 \times 31 + 1 = 62 + 1 = 63 $$
عدد بعدی دنباله $$ 2, 6 , 12, 20, ... $$ چیست؟
25
28
30
32
دنباله مورد سوال از قانون زیر پیروی میکند:
$$
\begin{aligned}
& 1 \times 2=2 \\
& 2 \times 3=6 \\
& 3 \times 4=12 \\
& 4 \times 5=20
\end{aligned}
$$
عدد اول این دنبال 1 است. عدد دوم از ضرب عدد 2 در عدد 1 و عدد سوم از ضرب عدد 3 در عدد 2 به دست میآید. در واقع، شماره هر عدد در عدد بعدی ضرب میشود. به این ترتیب برای عدد بعدی (عدد پنجم)، خواهیم داشت:
$$ 5 \times 6 = 30 $$
البته امکان پیروی دنباله از قوانین دیگر نیز وجود دارد. به عنوان مثال میتوان با استفاده از قانون زیر به جواب رسید:
$$
\begin{aligned}
& 2 + 4=6 \\
& 6 + 6=12 \\
& 12 + 8=20 \\
\end{aligned}
$$
در این جا، عدد دوم از جمع عدد اول (2) با عدد 4 به دست میآید. سپس، حاصل این عدد با عدد 6 (جمع عدد 4 و 2) برابر میشود. حاصل این عدد (12) نیز با جمع آن با عدد 8 (جمع عدد 6 و 2) برابری میکند. بنابراین، عدد بعدی، برابر خواهد بود با:
$$
\begin{aligned}
& 2 + 4=6 \\
& 6 + 6=12 \\
& 12 + 8=20 \\
& 20 + 10=30
\end{aligned}
$$
اعداد 0، 1، 1 و 2، اعداد اول تا چهارم دنباله فیبوناچی هستند؟ عدد دوازدهم از این دنباله کدام است؟
55
77
88
89
اعداد سوم به بعد در فیبوناچی، از جمع دو عدد قبلی خود به دست میآیند:
$$
\begin{aligned}
& 0 \\
& 1\\
& 1 + 0 = 1 \\
& 1 + 1 = 2 \\
& 2 + 1 =3 \\
& 3 + 2=5 \\
& 5 + 3=8 \\
& 8 + 5=13\\
& 13 + 8=21\\
& 21 + 13=34\\
& 34 + 21=55\\
&55 + 34=89\\
\end{aligned}
$$
بنابراین، عدد دوازدهم در دنباله فیبوناچی برابر با 89 است.
سایر دنبالهها
توجه کنید که در ریاضیات، دنبالههای بسیار زیادی وجود دارند و شما حتی میتوانید برای خود یک دنباله درست کنید! البته در آینده در مورد سریهای بینهایت نیز صحبت خواهد شد.










سلام فرمول ۱ ۲ ۴ ۸ ۱۶ …..چی میشه
سلام دوست عزیز.
ببین باید با چند فرمولیستیشن خاص بری
ضابطه این عدد باید با هندسی بری یعنی:
بهش توان میدی همین n_1که پایین نوشتم توان r هست با هندسی یعنی تقسیم.
«an= a1 r «n_1.
و ضابطه بازگشتی: anکه پایین گذاشتم با خط کسری تقسیم بر an+1 سمت راستش میکنی همین اینم ضابطه بازگشتی..
an+1= an ,an+1
2^n
2 به توان عدد
رابطه این دو الگو چیست؟
21_25_28_30
و
18_25_32
-1
-2
-3
-4
الگو …,3,6,11چی میشه؟؟
کسی میدونه عدد بعدیه این دنباله چی میشه دو ، چهار ، نه ، پانزده ، بیست و هشت ، پنجاه و دو ، ؟
۹۵
این چه الگویی هست. (…_۲۶_۱۵_۷_۲)
و رابطه اش چی هست؟
درجه دو
1.5n2+0/5n
سلام رابطه 2 و 6 و 15 و 64 و ؟ ادامه چند هستش؟
سلام لطفا فرمول اين الگو چيه؟ 2.6.14.24.؟
درالگوی۹،۱۰،۲۰،۱۲۰ ادامه الگو چی میشه
میشه جواب الگو های 1,4,10
جمله n ام الگوی زیر چیه ؟؟
۶۴،۳۲،۱۶،۸،۴،۲
سلام ببخشید فرمول این الگو چیه
۴،۹،۱۵
یه دنباله که برای بسته بندی اجسام گرد یا حتی مکعب و… میشه بکار برد دنباله ای که خودم کشفش کردم و اسمشو گذاشتم دنباله تخم مرغی هست که از مضرب ۳و ۴ درست میشه به این شکل که اگه به این دو عدد تقسم پذیر باشه میشه تو یه بسته جاشون داد
3-7-8-21-49-76-224-467-514
کسی میتونه ادامه این و بدست بیاره؟؟یا فرمول شو
میشه الگوی۱۳.۱۹.۲۵ رو بگید
5-10-19-31-32-9-10
سلام وقتتون بخیر
ممنون میشم اگر براتون مقدور هست الگو این و بگید سپاس از شما
سلام میشه6n+7
الگو …1.1.4.3.9.6.16.1
میشه حل کنید لطفا
عالی بود
دنباله ۴ ۴ ۱۰ ۲۸ .. رو توضیح بدید
این الگو …1.1.4.3.9.6.16.16
ممنون می شم این الگو رو حل کنی
کسی میدونه ادامه این دنباله چی میشه
۱، ۲ ، ۶ ، ۲۱ ، ۸۸،….
۵×۵=۲۵الگوهای مربعی با فرمولn,n
سلام ببخشید ادامه ی الگوی عددی زیر رو میگید ممنون:۴،۹،۱۴،۱۹
سلام وقتتون بخیر
کسی میدونه جمله عمومی دنباله …،۲،۳،۵،۷ چی میشه؟
سلام میشه لطفا رابطه ی الگوی زیر رو بگید؟:
۶،۱۹،۲۱،۴۲…
۴و۸و۱۵و۲۸و….فرمول محاسبه
5+
ِِan=a1+(n-1) d
a1=4
d=5
جمله عمومی
5n-1
سلام و روز شما به خیر؛
به نظر میرسد هر جملهای در دنباله شما از جمع عدد ۵ با عدد قبلی دنباله حاصل میشود. در حقیقت داریم: $$a_{n+1}=a_{n}+5$$
از همراهی شما با فرادرس خرسندیم.
۱ بعلاوه ۲ بعلاوه ۳ بعلاوه چهار الگوش چی میشه
اگه میشه الگوی
1,5,12,22
چی میشه لطفا سریع
سلام دوستان . این دنباله اعداد فرمول خاصی داره . مثلا بخواییم عدد 25 ام رو حساب کنید . فرمول داره ؟ 8.20.36.56
میشه لطفا رابطه ۳،۵،۸،۱۱،۱۷،۲۶،۴۱ رو بگید
ببخشید میشه رابطه ی ۳،۸،۱۳،۱۸روبگید؟؟برای کلاس ششم
خوبه سوالی ندارم
دنباله ی (۵,۵,۵,۵,…) چه دنباله ایه…؟؟؟؟
کسی میدونه؟؟؟؟؟
دنباله -1 2 5 8 11 رو میشه پیدا کنید
سلام اگه دقت کنیم همه به اضافه سه شدن یعنی الگوی منظمه و نکتش هم اینه شماره شکل ضرب در فاصله به اضافه منها یا هیچکدوم حالا این چطور رفته جلو گفته منفی سه به اضافه سه میشه دو اگه امسال پایه شش باشی میخونی درباره ی منفی و دو به اضافه سه شده پنج و همینطوری ادامه پیدا کرده.
سلام من یه سوال داشتم
عدد بعدی این دنباله چی میشه (جواب 110 نیست)
101-102-103-104-105-106-107-108-109
۱۰۱۰
?,۱,۷,۱۹,۶۱
جوابش بصورت زیر میشه
1+6*1
2+5*7
3+4*19
4+3*61=247
میشه ۱۰۱۰
سلام. به نظرتون جوابش ۱۰۱۰ نمی شه؟
سلام وقت بخیر لطفا در صورت امکان حل نمایید ؟
?,1,7,19,61
جواب ۲۴۷ هست فقط روش بدست آوردن رو نمی دانم .
پاسخ روپیدا کردین؟
پس فرمواشون کجاست؟
مثلا اگه بگن جمله n ام این الگو چیه؟
آیا میشه اینطوری جواب رو پیدا کرد؟
رابطه ی بین
۲ و ۹ و ۶۴ و ۶۲۵
چیست؟
معمولا جمله ی ان امش کار خاصی نداره
فقط باید جمله ی اول و قدر نسبت رو داشته باشی…
برای دنباله های حسابی جمله انم میشه: a¹+(n-1)d
دی قدرنسبته-_-
برای دنباله های هندسی هم جمله انم میشه جمله اول ضربدر قدر نسبت به توان ان منهای یک….
اگه بازم باشه من نمیدونم
ヽ(ˇヘˇ)ノ
الگوی …1,6,11,16
رو نمیتونم پیدا کنم میشه کمکم کنید
سلام.
فرمول الگوی زیر چی میشه؟
1_4_8_13_19_26_34
ریاضی کلاس چهارم
a¹=1
d=a²-a¹=5
جمله عمومیش هم میشه : an= a¹+d(n-1)
خب ببین خیلی سادس گفته 16 11 6 1 الان یک به اضافه پنج شده بعد شش به اضافه پنج شده شده یازده بعد هم یازده به اضافه پنج شده اگه متوجه شده باشی این الگوی منظم هستش و نکتش هم اینه شماره شکل ضرب در فاصله به اضافه منها یا هیچکدوم یعنی نه به اضافه منها میکنیم نههیچی فقط شماره شکل ضرب در فاصله حالا اگه میخوای کامل یاد بگیری که چطور بدونیم به اضافه منها بکنیم یا نه.
شماره عدد ضربدر پنج منهای چهار
۵ تا ۵ تا میره جلو
بعدش میشه ۲۱ بعد ۲۶
الگوی …1,6,11,16
رو نمیتونم پیدا کنم میشه کمکم کنید
الگوی آن بدین صورت است:
y = 5x – 4
که در آن x شماره عنصر مدنظر و y مقدار آن می باشد.
اگر دقت کنید ، می بینید که اعداد در این الگو ۵ تا ۵ تا اضافه می شوند ، پس ضریب x برابر ۵ می شود و اینک اگر مقدار عنصر اول را جایگزین y کنیم و سپس معادله را حل کنیم ، جواب معادله ۴- می شود که آنرا در کنار 5x می نویسیم.
سلام من دنبال یه رابطه کلی هستم ، مثلا برای الگوهای جمع یه رابطه ضرب وجود داره ،
یعنی اگه دنباله ما این شکلی باشه : ۱,۶,۱۱,۱۶,۲۱
هر عدد به علاوه ۵ شده
فرمول کلیش میشه5n+?
و کافیه n رو اولین عدد دنباله قرار بدیم . حالا برای الگو های چند طبقه هم هست ولی هرچی میگردم پیداش نمیکنم ، ولی مطمعنم ، مثلا برای دنباله ضرب ، توان وجود داره ، همچنین از این فرمول ها میشه تو الگو های که اول جمع شدن بعد ضرب شدن بعد نمیدونم تقسیم شدن و.. بطور کلی الگو های پیچیده تری استفاده کرد اما کاملش رو پیدا نمیکنم !
۲۳،۱۵،۲۲،۵۸،۲۲۴،…..،…..
سلام لطفاً فرمول این الگو را بدید
سلام
۵،۷،۱۴،۱۶،۳۲
این دنباله حساب میشه یا ن؟
اگر میشه چ نوع دنباله ایه
سلام.
در این دنباله، عدد ۲ یکیدرمیان با عدد جمع و در آن ضرب میشود:
$$ \begin {align*}
5 + 2 &= 7 \\
7 \times 2 &= 14 \\
14 + 2 &= 16 \\
16 \times 2 &= 32 \\
32 + 2 &= 34 \\
34 \times 2 & = 68 \\
\vdots
\end {align*} $$
موفق باشید.
خب ببین این الگوی منظمه پس باید برای اینکه عدد های بعدی رو پیدا کنیم یه نکته دداشته باشیم که میشه شماره شکل ضرب در فاصله به اضافه منها یا هیچکدوم برای اندیا توضیح دادم.
لطفاً لطفاً لطفاً این را بگید
1 4 7
لطفاًجواب این الگوها رابفرمایید
،…..،۸،۱۴،۲۶
،….،۴،۵،۸
الگو بین
1.4.10.20.35 و…
چیه؟
میشه کمکم کنین
سلام
من یه مسئله دارم که میگه
الگوریتمی بنویسیدکه یکعددازnوردی گرفته و nجمله اول دنباله ی زیرراتولید و نمایش دهد
0,1,3,6,10,15,…..
اگر جمله اول a باشه
و جمله دوم برابر s1+b=s2
و جمله سوم برابر s2+c=s3 که در تمام جملات بعدی مقدار c-b عددی ثابت و برابر d باشد خواهیم داشت
sn=An^2+Bn+C
که A=d/2
B=b-3d/2
C=d+a-b
ببخشید این چه الگویی هستش و عدد بعدش چه عددیه؟
…,1,1,2,2
میشه ۴
سلام رابطه این الگو چیست؟؟
۱۲و۶و۴و۳
باسلام
لطفاً رابطه الگوی زیر را بفرمائید.
1 5 14 30 ۵۵ ۹۱ و…..
شکل پانزدهم ۱۲۴۰ میشه. رابطه را میخوام.
ممنون
میشه 36 گلم
بعد الگوی ۱،۲،۴،۱۲،۱۵،۶۰ چیه لطفا بگید
لطفا بگید چطور {…،۵،۱۰،۱۵،۲۰} را به زبان ریاضی بنویسم
با سلام اگ میشه عدد بعدی این دنباله و الگوشو بگین چی میشه با تشکر
۵-۸-۱۲-۱۶-۲۲-۲۶-۳۲
۹،۱۴.۲۰،…..
سلام ما یه فرمول کلی داشتیم که طولانی بود ولی برای همه الگو ها صدق میکرد و چیزایی که ازش یادمه اینه که یه بار اختلاف بین اعداد رو به دست میاوردیم و دوباره اختلاف بین اونها رو به دست میاوردیم و تو یه معادله هایی میزاشتیم و حل میکردیم اگه از اون فرمول آگاهی دارین میشه توضیح بدینش من اینو چند سال پیش خونده بودم و الان به کلی درسای اون موقع رو یادم رفته
سلام جمله ی عمومی دنباله ی۵،۸،۱۵،۲۴و…چطوری بدست میاد؟
الگوی
۲،۷،۱۵،۳۱،بعدیش؟؟؟
سلام ببخشید ادامه الگوی زیر چی می شه
۴۱_۲۱_۱۱_۶
ضربدر 2 منها 1
یکی مدیر سایت باشه که بتونه به سوالا جواب بده!!!! فقط به یه یوال ساده تونستی جواب بدی
سلام ممنون از راهنمایی های خوبتون
اگر در الگوی مثلثی یا مربعی، اعداد از عددی غیر از 1 شروع شود، فرمول چه تغییری خواهد کرد؟
مثل
3،6،10،15
یا
9،16،25
لطفا الگوی عددی زیر را ادامه دهید؟
5 19 16 39 49
سلام
ممنون، استفاده کردم
سلام،لطفاا الگوی عددی زیر رو بفرمایید
۲،۶،۹،۲۷
سلام و روز شما به خیر؛
به نظر میرسد دنباله یکی در میان در سه ضرب و برای عدد بعد با سه جمع میشود. در حقیقت $$2\times 3=6$$ُ، $$6+3=9$$ و $$9 \times 3 =27 به دست میآید، یا می توان گفت اعداد با جایگاه فرد با ۳ جمع شده و اعداد در جایگاه زوج در ۳ ضرب میشوند.
از همراهی شما با فرادرس خرسندیم.
سلام
این دنباله از چه نوعیه و جمله عمومیش چیه؟ممنون
3-5-14-55-274
لطفا جواب بدید الگوی ،۱،۴،۱۳،۴۰
عدد قبلی ضربدر ۳ بعلاوه یک عدد بعدی ۱۲۱ میشه
عزیزم جواب این دنباله????
(شماره ی شکل × فاصله)
سلام. الگوی این دنباله به صورت زیر است:
$$ \begin{align*}
0+3^0 &= 1\\
1 + 3^1 &= 4\\
4+ 3^2 &= 13 \\
13 + 3^3&=40 \\
& \vdots
\end{align*}$$
یک روش برای جمع این دنباله می خوام
۳۱_ ، ۳۷_ ، ۰۰۰ ، ۱۸۱_ ، ۱۸۷_ ، ۱۹۳_
ممنون از توضیحات . ولی چرا برای هر دنباله فرمولی مشخص نکردید. مثلا جمله پانصدم یک دنباله چند هست؟
جمله عمومی 1 و 2 و 3 و 5 و…
چیه؟
یا حالا همون فرمولش
سلام پاسخ الگوی زیر رو میتونید بهم بگید
3،5،14،55
سلام
لطفا راهنمایی کنید جواب چیه ممنون
533. .1.1.2.4.11
جواب داخل این عدداد هستش
83.90.123.161.48
سلام
لطفا راهنمایی کنید:عدد بعدی این دنباله چیست؟
0 , 1 , 3 , 4 , 12 , 13 , ?
سلام
فرمول کلی دنباله ی -2,,-2,,0,,4 چیه؟
۵.۱۱.۸.۳۱.۱۱اینو اگه میشه جواب بدین عدد بعدیش چی میشه.چطوری بدست میاد
سلام ممکن است در ساخت این سری به من کمک کنید فرمول ساخت این سری را نمی توانم بدست اورم
۱-۱/۲+۱/۳_۱/۴….
۵،۳،۶،۹،۹ عدد بعدی این دنباله چیه
چ فرمولی داره
میشه لطفا به من بگید جواب این چی میشه خیلی سریع فقط
81 یکمین عدد در الگوی زیر
1 و 2 و 2 و 3 و 3 و 3 و …….
الگوی عددی ۴،۹،۱۵ رو خیلی حل کردم ولی فرمولی پیدا نکردم میشه لطفا اگه فرمولش رو فهمیدید بگید؟
n^2+7n)÷2).
توضیح:
اولین عدد مساویست با ۴ ((۴×۱)+۰).
دومین عدد مساویست با ۹((۴×۲)+۱).
سوم: ۱۵((۳×۴)+۳).
همانطور که ملاحظه می کنید هر عدد برابر است با ۴n به علاوه اعدادی دیگر که به این ترتیب هستند:
۱) ۰ = 0
۲) ۰+۱ = 1
۳) ۰+۱+۲ = 3
که همان الگوی مثلثی است با این تفاوت که یک صفر به آن اضافه شده که باید به اندازه شماره شکل از آن کم کنیم (((n(n+1))÷2)-n).
در نتیجه جمله عمومی به این شکل به دست می آید (4n+(((n(n+1))÷2)-n) که با عملیات ساده جبری همان n^2+7n)÷2) به دست می آید.
این الگوی مثلثی هست که توی پایه پنجم هست یکی یکی اضافه میشه منظورم چچیه الان چهار به اضافه پنج شده میشه نه و نه هم به اضافه شش میشه پانزده و حالا به الگو یعنی عدد
هایی که اضافه میشن یکی یکی بهشون اضافه میشه پنج به اضافه یک شده و میشه ششو نکتش هم اینه شماره شکل ضرب در شماره شکل به اضافه یک تقسیم بر دو
خب در واقع فرمول اینه که شماره الگو هر عدد به علاوه یک(n+۱) به توان ۲
عدد چهار شماره اگوی یکمه پس یک به علاوه یک میشه دو وقتی به توان دو برسه میشه چهار
عدد نه شماره دومه الگو هس پس به علاوه یک میشه سه وقتی به توان دو برسه میشه نه
عدد شونزده شماره سه اگو هس پس به علاوه یک میشه چهار وقتی به توان دو برسه میشه شونزده
عدد الگو چهارم رو نداریم برا به دست اومدنش چهار به علاوه یک می کنیم که میشه پنج و وقتی به توان دو برسه میشه بیست و پنج
و همین جور الی آخر
محیط مستطیلی ۳۷۰ است اگر طول آن از دو برابر ارزش ۴۰ واحد کمتر باشد مساحت آن چه قدر است
سلام مخاطب گرامی؛
مطلب «مستطیل و محاسبات آن — به زبان ساده» به صورت دقیق به بیان روابط محیط و مساحت مستطیل پرداخته است.
سلام ببخشید خیلی وقت هست که دارم دنبال جواب این دنباله می گردم اگه می شه بهم بگید مرسی:…،۱،۲،۲،۳،۳،۳،۴،۴،۴،۴
اگه بهم ایمیل کنید ممنون می شم:shirbanshahia@gmail.com
سلام ببخشید فرمول این الگو چیه?
۱،۳،۳،۲،۲،۴،۴
عدد بعدی رو نمیخوام فراموش رو میخوام
به تعداد عدد ،عدد اضافه میشه مثلا عدد ۵ را پنج دفعه مینویسیم
بعدش میشه ۵این ک خیلیدساده است بعدش میشه پنج
فرمول کلی برای عددn: عدد فرضی در (عدد فرضی+1) تقسیم بر2 به علاوه عدد دیگر
مثلا عدد 121ام مساوی 15در16 تقسیم بر2 +1=پس جز اعداد 15 است یکی بشتر یعنی اولین پانزده نه دومین پانزده
خب این
یکی یکی میره
از عدد یک، یه دونه هست از عدد دو ،دو تا از عدد سه ،سه تا
اما اگه بگه صدمینش چیه رو نمیدونم