توزیع های آماری F و T — مفاهیم و کاربردها

در این نوشتار به بررسی توزیع‌هایی می‌پردازیم که براساس یک نمونه تصادفی حاصل می‌شوند و در آزمون‌های مربوط به پارامترهای جامعه کاربرد دارند. برای مثال از توزیع نمونه‌ای F برای آزمون نسبت واریانس دو جامعه استفاده می‌شود و همچنین از توزیع T نیز برای آزمون‌هایی که مربوط به میانگین جامعه است بهره می‌برند.

از آنجایی که در این نوشتار از متغیر تصادفی و تابع احتمال صحبت به میان خواهد آمد بهتر است ابتدا مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال را مطالعه کرده باشید. همچنین اگر به مباحث مربوط به آزمون فرض که توسط آماره‌هایی با توزیع F و T صورت می‌پذیر علاقه‌مندید بهتر است مطلب آزمون‌های فرض و استنباط آماری — مفاهیم و اصطلاحات را بخوانید تا با آمادگی کامل به بررسی این توزیع‌ها بپردازیم.

توزیع F یا F- Distribution

توزیع F یا توزیع فیشر-سندکور (Fisher-Snedecor) یک توزیع احتمال پیوسته است که بیشتر برای آزمون‌های فرض مربوط به تحلیل واریانس (ANOVA) به کار می‌رود. این توزیع براساس تحقیقات «رونالد فیشر» (Ronald Fisher) و «جورج سندکور» (George Snedecore) ابداع و خصوصیات آن بررسی و ارائه شد.

فیلم آموزش مفاهیم آماری در داده کاوی و پیاده سازی آن در پایتون Python در فرادرس

کلیک کنید

تعریف توزیع F

اگر X دارای توزیع F با پارامترهای $$d_1$$ و $$d_2$$ باشد، می‌نویسیم $$X\sim F(d_1,d_2)$$ در این حالت تابع احتمال این متغیر تصادفی X با مقدارهای مثبت (x>0) به صورت زیر خواهد بود:

$$\large \displaystyle f(x;d_1,d_2)=\frac{\sqrt{\frac{(d_1x)^{d_1}d_2^{d_2}}{(d_1x+d_2)^{d_1+d_2}}}}{xB(\frac{d_1}{2},\frac{d_2}{2})}$$

که منظور از B همان تابع بتا است. مقدار پارامترهای $$d_1$$ و $$d_2$$ نیز اغلب صحیح و نامنفی هستند. ولی در بعضی از مواقع ممکن است که به جای اعداد صحیح، پارامترهای توزیع مقدارهای حقیقی مثبت باشند. اغلب این پارامترها را درجه آزادی توزیع F می‌نامند.

نکته: با توجه به تعریف ارائه شده، مشخص است که تکیه‌گاه متغیر تصادفی F مجموعه اعداد حقیقی مثبت است.

در تصویر زیر نمودار مربوط به تابع چگالی این توزیع ترسیم شده است. همانطور که در تصویر مشخص است تابع چگالی احتمال این متغیر تصادفی برای درجه‌های آزادی کوچک، دارای میزان چولگی (Skewness) زیادی است ولی با افزایش درجه آزادی $$d_1$$ و $$d_2$$، منحنی تابع چگالی به شکل توزیع نرمال با میانگین و واریانس که در زیر معرفی شده، نزدیک می‌شود.

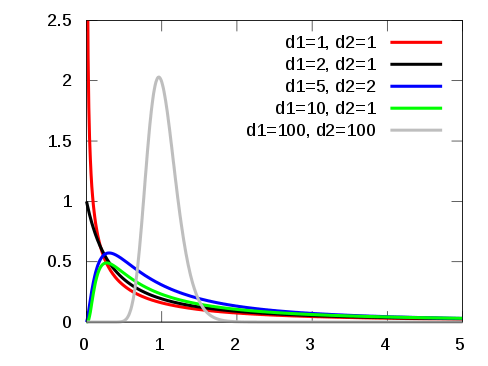
امید ریاضی و واریانس

بر اساس تابع چگالی و توزیع متغیر تصادفی، می‌توان امید ریاضی و واریانس متغیر تصادفی F را برحسب پارامترهای آن محاسبه کرد.

$$\large E(X)=\dfrac{d_2}{d_2-2}$$

البته این امید ریاضی را به شرطی می‌توان محاسبه کرد که $$d_2>2$$ باشد (اگر $$d_2=2$$ باشد که مخرج صفر خواهد شد و اگر هم مقدارش برابر با ۱ باشد امید ریاضی مقدارهای مثبت، عددی منفی بدست می‌آید که به نظر صحیح نخواهد بود). همانطور که دیده می‌شود، امید ریاضی متغیر تصادفی با توزیع F فقط به درجه آزادی دوم یعنی $$d_2$$ وابسته است و $$d_1$$ در آن نقشی ندارد.

$$\large Var(X)=\dfrac{2d_2^2(d_1+d_2-2)}{d_1(d_2-2)^2(d_2-4)}$$

البته رابطه مربوط به محاسبه واریانس، به شرطی برقرار است که $$d_2>4$$ باشد زیرا اگر درجه آزادی $$d_2$$ برابر با ۲ یا ۴ باشد مخرج صفر خواهد شد و اگر از ۴ نیز کوچکتر باشد، مخرج منفی شده و باعث می‌شود که واریانس مقداری کوچکتر از صفر بدست آید. در تصویر زیر نمودار تابع توزیع تجمعی متغیر تصادفی F ترسیم شده است. باز هم مشخص است که با افزایش درجه‌های آزادی توزیع F، شکل تابع توزیع تجمعی به نرمال نزدیک خواهد شد.

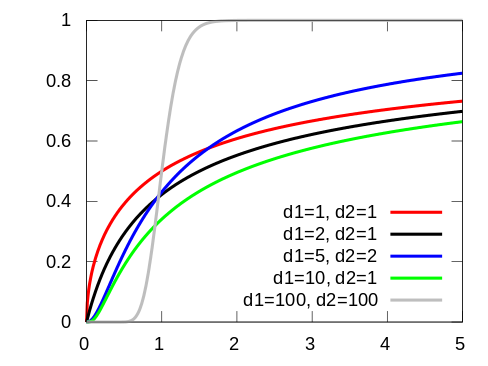
خصوصیات توزیع F

اگر $$U_1$$ و $$U_2$$ دو متغیر تصادفی با توزیع کای-۲ (Chi Square) باشند، آنگاه X که به صورت زیر معرفی شده است دارای توزیع F با پارامترهای $$d_1$$ و $$d_2$$ است.

$$\large X=\dfrac{U_1/d_1}{U_2/d_2}$$

نکته: در اینجا فرض شده است که متغیرهای تصادفی $$U_1$$ و $$U_2$$‌ مستقل از یکدیگرند. در غیر اینصورت نمی‌توان توزیع این نسبت را F در نظر گرفت.

از طرف دیگر با توجه به واریانس نمونه‌ای و واریانس جامعه می‌توان متغیر تصادفی F را براساس دو جامعه نرمال، تقسیم نسبت واریانس نمونه‌ای به واریانس جامعه برای توزیع اول به نسبت واریانس نمونه‌ای به واریانس جامعه برای توزیع دوم در نظر گرفت. پس:

$$\large X=\dfrac{s_1^2}{\sigma_1^2}/\dfrac{s_2^2}{\sigma_2^2}$$

نکته: در اینجا نیز باید $$s_1^2=\dfrac{S_1^2}{d_1}$$ و $$s_۲^2=\dfrac{S_۲^2}{d_۲}$$ باشد. زیر می‌دانیم که براساس واریانس نمونه‌ای $$S^2$$:

$$\large (n-1)S^2/\sigma^2\sim \chi^2_{(n-1)}$$

به این معنی که سمت چپ دارای توزیع کای-۲ با n-1 درجه آزادی است.

با توجه به تعریفی که برای متغیر تصادفی F در این قسمت ارائه شد، مشخص است که برای آزمون نسبت واریانس دو جامعه نرمال باید از توزیع F استفاده کرد.

از خصوصیات دیگر این توزیع می‌توان به موارد زیر اشاره کرد.

• اگر X دارای توزیع بتا با پارامترهای $$(d_1/2,d_2/2)$$ باشد، یعنی داشته باشیم $$X\sim Beta(d_1/2,d_2/2)$$، آنگاه :

$$\large \dfrac{d_2X}{d_1(1-X)}\sim F(d_1,d_2)$$

• اگر متغیر تصادفی $$X\sim F(d_1,d_2)$$ آنگاه، $$X^{-1}=\dfrac{1}{X}\; \sim F(d_2,d_1)$$
• اگر X دارای توزیع T با درجه آزادی n باشد، آنگاه $$X^2\sim F(1,n)$$ و $$X^{-2}=\dfrac{1}{X^2}\;\sim F(n,1)$$ خواهد بود.

استفاده از جدول تابع احتمال متغیر تصادفی F

برای محاسبه مقدار احتمال یا احتمال تجمعی یک متغیر تصادفی با توزیع F از جدول‌های بخصوصی استفاده می‌شود. برای مثال اگر بخواهیم به ازاء مقدارهای مختلف درجه آزادی‌های توزیع F مقدار تابع چگالی احتمال را در نقطه X=0.5 محاسبه کنید، جدول زیر مناسب به نظر می‌رسد.

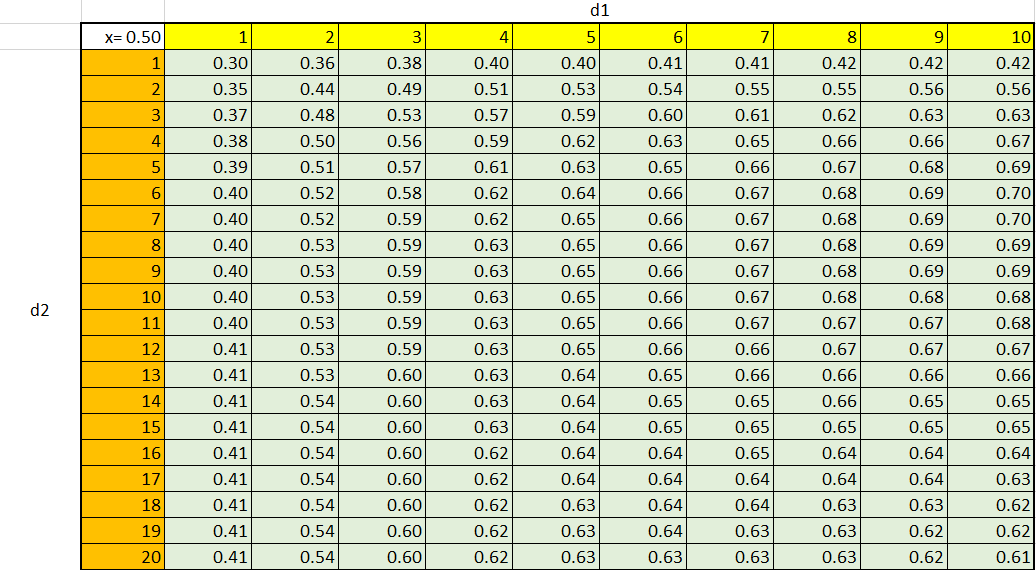
ولی گاهی باید برعکس عمل کنیم و بخصوص برای انجام آزمون‌های آماری به صدک‌های توزیع F احتیاج داریم. برای این منظور نیز می‌توان از جدول‌هایی استفاده کرد که برحسب صدک‌ها و محاسبه احتمال تجمعی بالایی یا پایینی ایجاد شده‌اند. در تصویر زیر میزان احتمال صدک 9۵ام دیده می‌شود. (در اینجا $$\alpha=0.05$$ به معنی P(X>x)=0.05 است.)

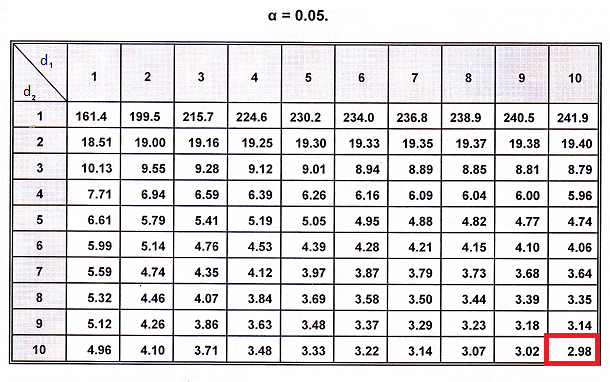
تصویر زیر، سطح زیر منحنی توزیع F را که مطابق با جدول بالا است را نمایش می‌دهد.

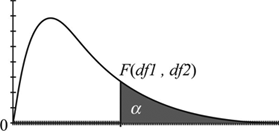
البته برای محاسبه مقدار تابع چگالی و یا صدک‌های توزیع F‌ از اکسل نیز می‌توان کمک گرفت. در ادامه به بررسی توابعی که این کار را انجام می‌دهند می‌پردازیم.

فرض کنید بخواهیم صدک 95ام توزیع F را برای $$d_1=10,d_2=10$$ بدست آوریم. کافی است تابع F.INV را با پارامترهای میزان آلفا ($$\alpha$$) و درجه‌های آزادی اجرا کنید.

$$\large F.INV(0.95,10,10)=2.9782$$

همانطور که دیده می‌شود، این مقدار با جدول بالا که مربوط به صدک‌هایی بالایی است مطابقت دارد. در اینجا منظور از صدک ۹۵ام مقداری است که احتمال بزرگتر از آن مقدار برابر با 0.95-1=0.05 باشد. برای محاسبه تابع توزیع احتمال یا تابع توزیع احتمال تجمعی نیز از تابع F.Dist با پارامترهای x و درجه‌های آزادی می‌توان استفاده کرد. برای مثال برای محاسبه تابع احتمال تجمعی تا نقطه 2.9782، برای توزیع F با درجه‌های آزادی ۱۰ و ۱۰، تابع را به صورت زیر می‌نویسیم:

$$\large F.DIST(2.9782,10,10,True)=0.9499$$

که نشان می‌دهد مقدار 2.9782 تقریبا همان صدک 95 است زیرا احتمال محاسبه شده بسیار به 0.95 نزدیک است.

نکته: توجه داشته باشید که پارامتر True نشان می‌دهد که اکسل باید تابع احتمال تجمعی را محاسبه کند. با در نظر گرفتن مقدار False برای این پارامتر، تابع احتمال (تابع چگالی) در نقطه x محاسبه می‌شود. جدول زیر توابع مرتبط با توزیع F در اکسل را معرفی کرده است.

نکته: با توجه به شکلی تابع توزیع F می‌توان گفت که با جابجایی درجه‌های آزادی می‌توان نوشت:

$$\large F_{\alpha}(d_1,d_2)=\dfrac{1}{F_{1-\alpha}(d_2,d_1)}$$

به این معنی که صدک $$\alpha$$ام برای توزیع F با درجه آزادی $$d_1$$ و $$d_2$$ با عکس صدک $$1-\alpha$$ام توزیع F با درجه آزادی $$d_2$$ و $$d_1$$ برابر است. برای مثال به رابطه زیر توجه کنید:

$$\large F_{0.05}(5,3)=0.1849=\dfrac{1}{F_{1-0.05}(3,5)}=\dfrac{1}{5.0495}=0.1849$$

توزیع student's-t

در آمار و احتمالات، توزیع و آماره T بسیار کاربرد دارد. بخصوص هنگامی که می‌خواهیم در مورد میانگین جامعه نرمال، آزمون فرض انجام دهیم ولی واریانس جامعه مشخص نیست. در این وضعیت آماره آزمون جدیدی به نام آماره T انتخاب شده و آزمون براساس آن صورت می‌گیرد. همچنین اگر اندازه نمونه کوچک باشد و نتوان از قضیه حد مرکزی استفاده کرد، توزیع جایگزین به جای توزیع نرمال می‌تواند توزیع t باشد.

فیلم آموزش نمایش اطلاعات آماری و توزیع ها در متلب (رایگان) در فرادرس

کلیک کنید

این توزیع براساس تحقیقات عملی دانشمند آمار، «ویلیام گُست» (William Sealy Gosset) معرفی گردید ولی از آنجایی که علاقه نداشت مقالاتش به اسم خودش باشد از اسم مستعار student استفاده می‌کرد. به همین دلیل این توزیع به نام student شهرت دارد.

تعریف توزیع نمونه‌ای t

اگر متغیر تصادفی X دارای توزیع t با $$\nu$$ درجه آزادی باشد می‌نویسیم: $$X\sim t(\nu)$$. فرض کنید $$X_1,X_2,\ldots,X_n$$ و iid با توزیع نرمال با پارامترهای $$\mu$$ و $$\sigma^2$$ باشند (شرط استقلال و هم توزیعی را با iid نشان می‌دهیم)، آنگاه اگر میانگین نمونه‌ای $$\overline{X}$$ و واریانس نمونه‌ای $$S^2$$ را به صورت زیر تعریف کنیم:

$$\large \overline{X}=1/n\sum_{i=1}^nX_i$$

$$\large S^2=\dfrac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2$$

خواهیم داشت:

$$\large \dfrac{\overline{X}-\mu}{S/\sqrt{n}}\sim t(n-1)$$

این متغیر تصادفی دارای توزیع t با n-1 درجه آزادی خواهد بود. شکل تابع چگالی احتمال این متغیر تصادفی به صورت زیر است:

$$\large {\displaystyle f(x)={\frac {\Gamma ({\frac {\nu +1}{2}})}{{\sqrt {\nu \pi }}\,\Gamma ({\frac {\nu }{2}})}}\left(1+{\frac {x^{2}}{\nu }}\right)^{\!-{\frac {\nu +1}{2}}}}$$

مشخص است که منظور از $$\Gamma$$، تابع گاما و $$\nu$$ نیز درجه آزادی توزیع t است.

نکته: به مانند توزیع نرمال، توزیع t نیز متقارن است زیرا در رابطه مربوط به تابع چگالی احتمال از $$X^2$$ استفاده شده است. همچنین باید توجه داشت که تکیه گاه متغیر تصادفی t، همه اعداد حقیقی است.

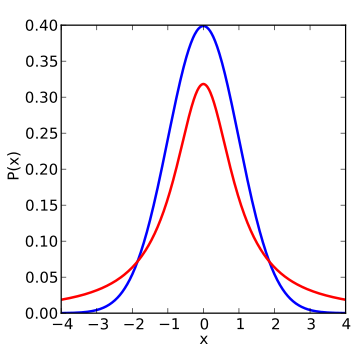
شکل منحنی تابع احتمال این متغیر تصادفی در زیر ترسیم شده است. منحنی آبی رنگ توزیع نرمال استاندارد و منحنی قرمز تابع احتمال متغیر تصادفی t را نشان می‌دهد. همانطور که دیده می‌شود به نظر می‌رسد دم‌های این توزیع نسبت به دم‌های انتهای توزیع نرمال استاندارد کمی کلفت‌تر است. به همین علت توزیع t را جز دسته توزیع‌های «دم سنگین» (Heavy Tail) قرار می‌دهند.

در تصاویر بعدی، منحنی‌هایی که به رنگ سبز متمایز شده‌اند، نمودار تابع احتمال در مرحله قبلی است که دارای درجه آزادی کمتری هستند.

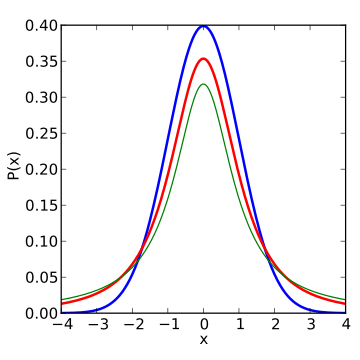
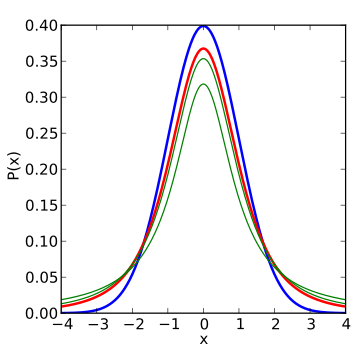
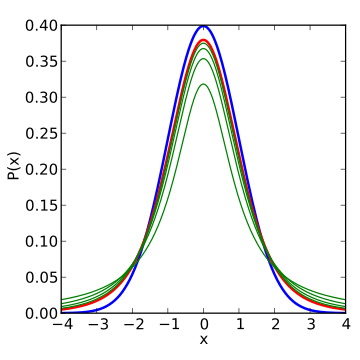
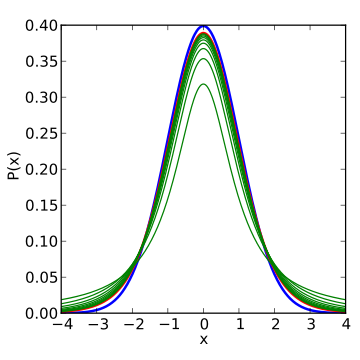
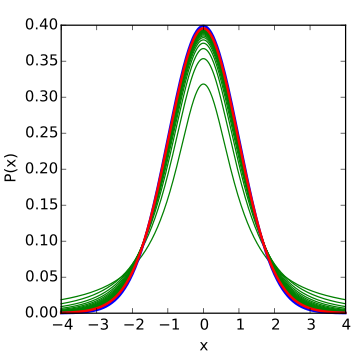
کاملا مشخص است که با افزایش درجه آزادی توزیع t، شکل نمودار احتمال به توزیع نرمال نزدیک خواهد شد. به همین علت برای زمانی که درجه آزادی بیشتر از ۳۰ باشد، می‌توان نمونه را برگرفته از جامعه نرمال در نظر گرفت. در تصویر زیر نیز شکل تابع توزیع تجمعی احتمال برای این متغیر تصادفی نمایش داده شده است.

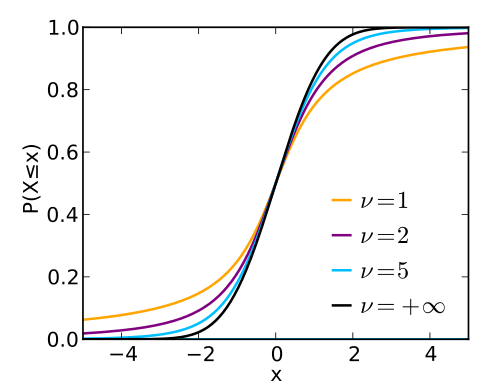
امید ریاضی و واریانس

با توجه به تقارن و مشابهت این توزیع با نرمال استاندارد مشخص است که میانگین، میانه و نما برای این توزیع نیز برابر با صفر خواهد بود.

فیلم آموزش مسائل تشریحی توزیع های گسسته و پیوسته در آمار و احتمال (رایگان) در فرادرس

کلیک کنید

پس امید ریاضی برای متغیر تصادفی با توزیع t برابر با صفر است (البته زمانی که درجه آزادی کمتر یا مساوی با ۱ باشد امید ریاضی تعریف نشده).

$$\large E(X)=\begin{cases}0 & \nu >1\\undefined & otherwise\end{cases}$$

واریانس نیز براساس درجه آزادی محاسبه شده و برابر است با

$$\large Var(X)=\begin{cases}\dfrac{\nu}{\nu-2} & \nu >2\\undefined & 1<\nu\leq 2 \end{cases}$$

خصوصیات توزیع t

فرض کنید:

• اگر Z یک متغیر تصادفی نرمال استاندارد (توزیع نرمالی که میانگین برابر با صفر و واریانس آن نیز برابر با ۱ باشد).
• V نیز یک متغیر تصادفی با توزیع کای ۲ با درجه آزادی $$\nu$$ باشد.
• ٰV مستقل از Z باشد.

در این صورت اگر داشته باشیم: $$\large T=\dfrac{Z}{(V/\nu)^{1/2}}$$ آنگاه $$\large T=\dfrac{Z}{(V/\nu)^{1/2}}\sim t(\nu)$$. همانطور که قبلا اشاره شد، می‌دانیم که متغیر تصادفی V که در پایین به آن اشاره شده است، دارای توزیع کای-۲ با n-1 درجه آزادی است.

$$\large{\displaystyle V=(n-1){\frac {S_{n}^{2}}{\sigma ^{2}}}}$$

از طرف دیگر نیز مشخص است که متغیر تصادفی Z که در رابطه زیر معرفی شده نیز دارای توزیع نرمال استاندارد است.

$$\large {\displaystyle Z=\left({\overline {X}}_{n}-\mu \right){\frac {\sqrt {n}}{\sigma}}}$$

نکته: توجه داشته باشید که تعریف $$S^2_n$$ و $$\overline{X}$$ در اینجا با تعریف ارائه شده در قسمت قبل به عنوان $$\overline{X}$$ و $$S^2$$ یکی است.

بنابراین با توجه به تعریفی که برای متغیر تصادفی با توزیع t ارائه شد، می‌توان گفت T که نسبت یک توزیع نرمال استاندارد به توزیع کای-۲ است دارای توزیع t با n-1‌ درجه آزادی است. این رابطه در زیر نشان بیان شده است.

$$\large {\displaystyle T\equiv {\frac {Z}{\sqrt {V/\nu }}}=\left({\overline {X}}_{n}-\mu \right){\frac {\sqrt {n}}{S_{n}}}}$$

از آنجایی که این آماره برحسب پارامتر مجهول جامعه ($$\mu$$) نوشته شده ولی توزیع آن به $$\mu$$ بستگی ندارد، می‌توان از آن به عنوان کمیت محوری برای ایجاد فاصله اطمینان استفاده کرد. از دیگر خصوصیات این توزیع می‌توان به موارد زیر نیز اشاره کرد:

• اگر $$X\sim t(\nu)$$ آنگاه $$X^2\sim F(1,\nu)$$ خواهد بود.
• اگر درجه آزادی برای توزیع t برابر با ۱ باشد، این توزیع را «کوشی» (Cauchy) با پارامترهای مرکزی (Location) برابر با ۰ و مقیاس (Scale) برابر با ۱ می‌نامند. از طرف دیگر اگر درجه آزادی به $$\infty$$ میل کند، توزیع متغیر تصادفی نرمال استاندارد خواهد بود.
• اگر Z با مقدار ثابتی جمع شده باشد، متغیر تصادفی حاصل را t-غیرمرکزی (Non-Centeral t Distribution) با مقدار پارامتر $$\mu$$ می‌نامند. در این حالت با توجه به تعریف گذشته می‌گوییم:

$$\large {\displaystyle (Z+\mu )(\frac {\nu }{V})^{1/2}\sim t_{\mu}(\nu)}$$

استفاده از جدول تابع احتمال متغیر تصادفی t

برای بدست آوردن مقدار تابع چگالی متغیر تصادفی t می‌توان از جدول‌های آماده استفاده کرد. در زیر یک نمونه از این جدول‌ها دیده می‌شود.

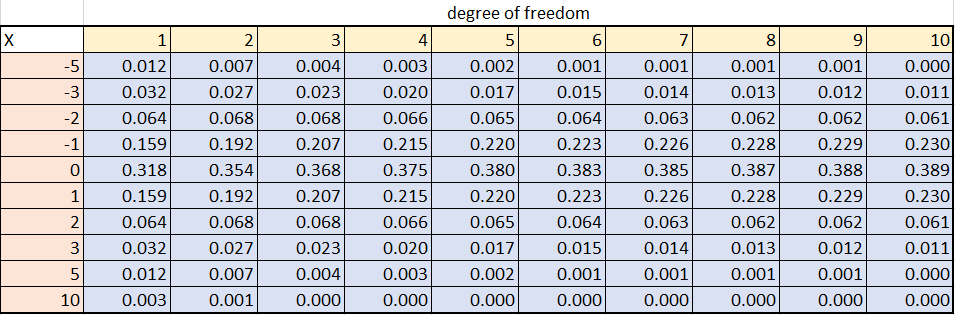
از طرفی برای انجام آزمون‌های آماری و یا تشکیل فاصله اطمینان برای میانگین جامعه احتیاج به صدک‌های توزیع t‌ است. استخراج این مقدارها به واسطه جدول‌های مانند جدول زیر امکان‌پذیر است.

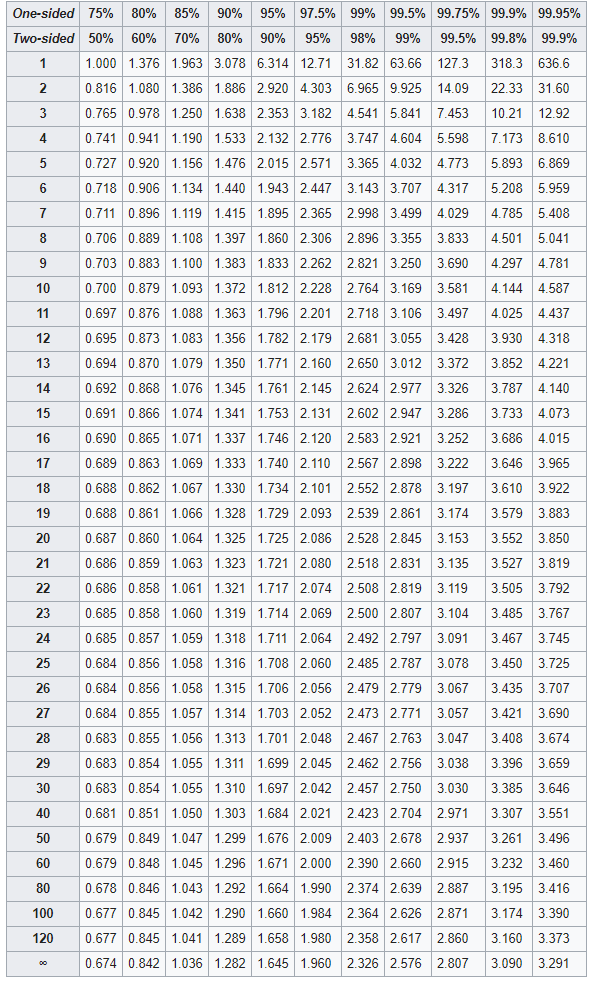
برای مثال، صدک 75ام برای توزیع t با درجه آزادی 30 برابر است با 0.683 که با مقایسه با همین صدک با توزیع نرمال استاندارد که برابر با 0.6744 است اختلاف اندکی وجود دارد. به همین ترتیب با افزایش درجه آزادی مشخص می‌شود که صدک‌های توزیع t به صدک‌های توزیع نرمال استاندارد نزدیک و نزدیک‌تر خواهند شد.

نکته: سطر اول این جدول مربوط به احتمال صدک‌ها است ولی سطر دوم بیانگر سطح اطمینان برای ایجاد فاصله اطمینان است.

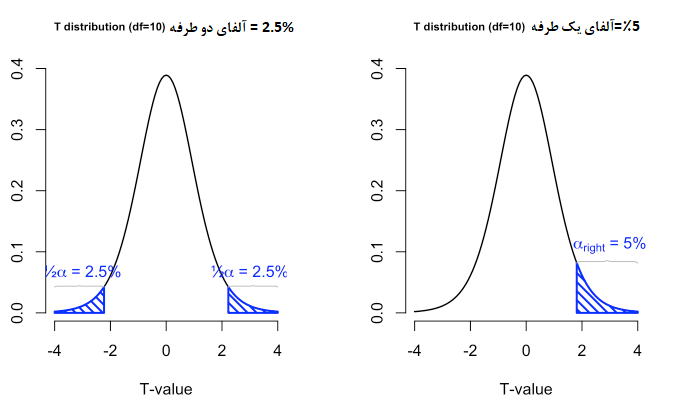
برای محاسبه مقدار تابع چگالی توزیع t و همچنین صدک‌های آن می‌توانید از اکسل کمک بگیرید. در ادامه به بررسی توابعی در این زمینه می‌پردازیم. فرض کنید که می‌خواهید مقدار چگالی احتمال متغیر تصادفی t با ۵ درجه آزادی را در نقطه x=2 محاسبه کنید. کافی است تابع T.DIST را با پارامترهای 2 و 5 , False اجرا کنید.

$$\large T.DIST(2,5,False)=0.06509$$

همانطور که در راهنمای این تابع می‌توان مشاهده کرد، مقدار بدست آمده با توجه به ناحیه سمت چپ منحنی چگالی استخراج شده است. همچنین برای محاسبه صدک ۵۰ام توزیع t با ۵ درجه آزادی کافی است تابع زیر را به کار برید:

$$\large T.INV(0.5,5)=0$$

از آنجایی که صدک ۵۰ام همان میانه است، مشخص می‌شود که برای توزیع t که تقارن نیز دارد، باید حاصل این تابع برابر با صفر باشد زیرا باید میانه را محاسبه کند. جدول زیر به معرفی توابعی از اکسل می‌پردازد که با توزیع t ارتباط دارند.

نکته: باید توجه داشت که برای تابع T.DIST.2T مقدار x باید مثبت باشد، در غیراینصورت، نتیجه فرمول با خطا مواجه خواهد شد.

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آزمایش تصادفی، پیشامد و تابع احتمال
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های SPSS
• مجموعه آموزش‌های نرم‌افزارهای آماری
• آموزش آزمون های فرض مربوط به میانگین جامعه نرمال در SPSS
• آموزش آزمون آماری و پی مقدار (p-value)
• جامعه آماری — انواع داده و مقیاس‌های آن‌ها
•  تحلیل‌ها و آزمون‌های آماری — مفاهیم و اصطلاحات
• آزمون فرض میانگین جامعه در آمار — به زبان ساده
• فاصله اطمینان (Confidence Interval) — به زبان ساده

^^