تعیین علامت عبارت های جبری و نامساوی ها – به زبان ساده

در این مطلب از مجله فرادرس در مورد تعیین علامت عبارت های جبری و نامساوی ها صحبت می‌کنیم. ریاضیات همیشه در مورد معادلات و تساوی‌ها نیست. گاهی نیز باید با نامعادلات یا نامساوی‌های که به صورت کوچکتر یا بزرگتر نوشته می‌شوند، محاسبات را انجام داد. با استفاده از تعیین علامت عبارت‌های جبری، پیدا کردن دامنه بعضی از توابع امکان پذیر می‌شود. بهتر است ابتدا با نمادهایی که در چنین حالاتی با آن‌ها سروکار داریم، آشنا شویم.

نکته: علامت $$\leq$$ هرگز نباید به صورت کوچکتر و مساوی خوانده شود، زیرا نمی‌توان تصور کرد که عدد x هم کوچکتر از y باشد و هم با آن مساوی باشد. بنابراین هنگام خواندن این نامساوی‌ها دقت کنید تا عبارت صحیح خوانده شود. این مورد برای علامت $$\geq$$ نیز صادق است و هرگز نباید به صورت بزرگتر و مساوی خوانده شود، بلکه باید به صورت بزرگتر یا مساوی گفته شود.

برای مثال اگر بنویسیم: «سن علی $$\leq$$ سن حسن» به این معنی است که علی سنش بیشتر یا مساوی با سن حسن است یا به بیان دیگر حسن سنش کوچکتر یا مساوی با سن علی است.

استفاده از نمادهای گفته شده در جدول، یک رابطه ترتیبی بین اعداد ایجاد می‌کند و می‌توانیم لیست‌های مرتب شده از آن‌ها ایجاد کنیم. در این حالت می‌توان این نمادها را معرف رابطه‌های ترتیبی روی اعداد در نظر گرفت.

نکته: برای اینکه علامت‌ یا نمادهای نامساوی و جهتشان را فراموش نکنید بهتر است از تصویر زیر کمک بگیرید.

نامساوی‌ و تعیین علامت عبارت‌های جبری

همانطور که در ابتدا متن دیده شد، نامساوی‌ها در ریاضیات بخصوص در محاسبات جبری بر روی عبارت‌های ریاضی، کاربردهای زیادی دارند. همانطور که در نوشته‌ قبلی فرادرس با عنوان معادله و نامعادله در ریاضی — پیدایش و کاربردها خواندید، منظور از حل یک معادله یا تساوی، پیدا کردن مقداری برای متغیر x است که تساوی به ازاء آن برقرار شود.

به همین ترتیب منظور از حل یک نامعادله یا نامساوی،‌ پیدا کردن مجموعه مقدارهایی برای متغیر x است که نامساوی برای آن‌ها برقرار باشد. از آنجایی که در حل نامساوی‌ها با علامت‌ها و محاسبات براساس آن‌ها سروکار داریم، بهتر است ابتدا قواعد کار با نامساوی‌ها را فرا بگیریم و سپس به تعیین علامت عبارت‌های جبری و حل نامساوی یا نامعادلات بپردازیم.

قواعد مربوط به نامساوی‌ها

برای حل یک نامساوی باید محاسبات جبری روی آن صورت گیرد. همانطور که می‌دانید، عملیات زیر تغییری در نامساوی‌ها ایجاد نخواهد کرد:

• اضافه کردن یک عبارت یا عدد به دو طرف نامساوی
• کم کردن یک عبارت یا عدد از دو طرف یک نامساوی
• ضرب کردن یک عبارت یا عدد مثبت به دو طرف یک نامساوی
• تقسیم کردن یک عبارت یا عدد مثبت به دو طرف یک نامساوی

ولی انجام هر یک از محاسبات زیر باعث تغییر در جهت نامساوی می‌شود.

• ضرب یک عبارت یا مقدار منفی به دو طرف نامساوی
• تقسیم دو طرف یک نامساوی به یک عبارت یا مقدار منفی.
• جابجایی عبارت‌های دو طرف نامساوی
• معکوس کردن عبارت‌های دو طرف نامساوی به شرطی که هر دو عبارت یا منفی یا هر دو مثبت باشند

برای درک بهتر به مثال‌هایی زیر توجه کنید:

مثال: فرض کنید باید نامساوی x+3<7 را حل کنید. اگر به دو طرف این نامساوی مقدار ۳- را اضافه کنیم، تغییری در آن بوجود نمی‌آید. بنابراین خواهیم داشت:

$$x+3<7\rightarrow x+3-3<7-3\rightarrow x+0<4\rightarrow x<4$$

نمایش عملیات بر روی محور اعداد نیز به درک روش حل مسئله کمک می‌کند.

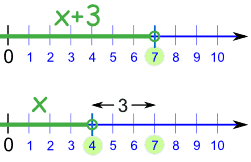
همانطور که مشخص است ناحیه مربوط به x+3<7 با کاهش ۳ واحد به سمت چپ (اضافه کردن عبارت ۳-) ناحیه مربوط به خود x را نشان می‌دهد.

توجه داشته باشید که اگر عبارت به صورت $$12$$ باشد، باز هم از همین روش می‌توان استفاده کرد. یعنی مراحل را به صورت زیر طی کنیم:

$$12$$

به این ترتیب با جابجا کردن دو عبارت این نامساوی می‌دانیم که علامت نیز تغییر خواهد کرد پس داریم $$x<7$$.

مثال: فرض کنید نامساوی به صورت $$3y<15$$ نوشته شده است. برای حل آن کافی است که دو طرف نامساوی را به ۳ تقسیم کنیم تا عبارت مجهول (y) به تنهایی در یک طرف نامساوی قرار گیرد.

$$3y<15\rightarrow 3y/3<15/3\rightarrow y<5$$

مثال: این بار ضریب مجهول را منفی در نظر می‌گیریم. نامساوی به صورت $$-2y<-8$$ است. برای حل آن مراحل را به صورت زیر انجام می‌‌دهیم.

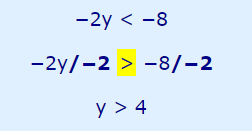
همانطور که مشخص است در مرحله دوم جهت نامساوی تغییر کرده است. زیرا دو طرف آن بر یک مقدار منفی تقسیم شده‌ است.

شاید برای شما این سوال پیش بیاید که چرا هنگام ضرب یا تقسیم دو طرف یک نامساوی در یک مقدار منفی، جهت تغییر می‌کند. پاسخ این است، بین دو عدد منفی x و y، عددی بزرگتر است که قدر مطلق آن کوچکتر از دیگری باشد. دو عدد ۳ و ۷ را در نظر بگیرید. این دو عدد هر دو مثبت هستند و داریم $$3<7$$ ولی زمانی که این دو عدد را در قرینه کنیم (در ۱- ضرب کنیم) دو مقدار ۳- و ۷- ایجاد می‌شود که نامساوی $$-7<-3$$ برایشان صادق است. همانطور که دیده می‌شود جهت نامساوی برعکس می‌شود.

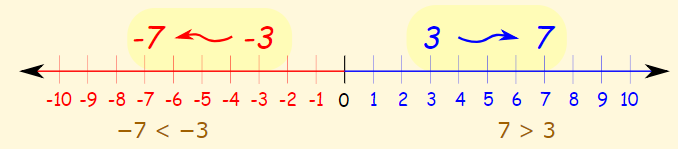
ضرب و تقسیم نامساوی در یک مقدار نامعلوم

فرض کنید که نامساوی به صورت $$bx<3b$$ باید حل شود. طبق معمول روال حل تساوی را در پیش می‌گیریم. باید متغیر x را به تنهای در یک طرف نامساوی قرار دهیم. پس دو طرف را به b تقسیم می‌کنیم. در نتیجه خواهیم داشت:

$$bx<3b\rightarrow bx/b<3b/b\rightarrow x<3$$

ولی این راه حل به تنهایی کافی نیست. در مراحل حلی که انجام شد، فرض بر این است که b مقدار مثبتی است. به همین دلیل جهت نامساوی تغییر نکرد. حال اگر b منفی در نظر گرفته شود، خواهیم داشت:

$$bx<3b\rightarrow bx/b>3b/b\rightarrow x>3$$

به نظر شما کدام جواب صحیح است؟ پاسخ این است، هر دو جواب صحیح هستند. انتخاب هر یک از آن‌ها بستگی به مثبت یا منفی بودن b دارد. پس پاسخ را به صورت زیر خواهیم نوشت:

$$\begin{cases}x<3 & b> 0\\x>3 & b < 0\end{cases}$$

توجه: هنگام تقسیم یا ضرب کردن یک نامساوی در مقداری که مثبت یا منفی بودن آن مشخص نیست، باید یکبار نامساوی را با فرض مثبت بودن و یکبار با فرض منفی بودن آن مقدار حل کرد و در نهایت پاسخ را برای هر دو شکل نمایش داد.

مثال: پاسخ نامساوی $$\dfrac{x-3}{2}<-5$$ چیست؟ منظور از پاسخ یک نامساوی، پیدا کردن مقدار یا فاصله از مقادیر است که با جایگزینی در x نامساوی برقرار باشد. پس در این مسئله به دنبال xهایی هستیم که با تفضلشان از ۳ و تقسیم نتیجه بر مقدار ۲، از ۵- کوچکتر باشند.

برای آنکه این نامساوی را به حالت ساده‌تری در بیاوریم، هر دو طرف نامساوی را در ۲ ضرب می‌کنیم تا کسر از بین برود. از آنجایی که مقدار ۲ مثبت است، تغییری در جهت نامساوی ایجاد نمی‌شود.

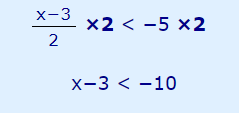
حال با اضافه کردن مقدار ۳ به دو طرف نامساوی، می‌توان ناحیه جواب برای نامساوی را پیدا کرد.

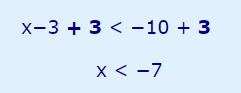
حل دو نامساوی بطور همزمان

اگر قرار باشد یک عبارت جبری را با دو نامساوی در نظر بگیریم، روش حل چنین نامساوی چگونه خواهد بود؟ شاید راحت‌ترین راه، شکستن یک نامساوی دوتایی به دو نامساوی باشد. به مثال زیر توجه کنید.

فیلم آموزش ریاضی صنف هفتم – ویژه دانش آموزان افغانستانی (رایگان) در فرادرس

کلیک کنید

مثال: پاسخ نامساوی $$-2<\dfrac{6-2x}{3}<4$$ چیست؟

برای پاسخ دادن به این سوال و پیدا کردن مجموعه مقدارهایی از x که هر دو نامساوی را پوشش دهند، ابتدا این نامساوی‌ها را تک به تک حل می‌کنیم. یعنی ابتدا نامساوی زیر را حل می‌کنیم:

$$-2<\dfrac{6-2x}{3}\rightarrow -2\times 3 <3\times \dfrac{6-2x}{3} \rightarrow -6<6-2x-6$$

$$\rightarrow -6-6<6-2x-6\;\;\rightarrow-12>2x\rightarrow \;\;12/2>2x/x\rightarrow 6>x\rightarrow x<6$$

سپس ناحیه جواب را برای نامساوی دوم تعیین می‌کنیم.

$$\dfrac{6-2x}{3}<4\rightarrow 3\times \dfrac{6-2x}{3}<3 \times 4 \rightarrow 6-2x<12$$

$$\rightarrow 6-2x-6<12-6\;\; \rightarrow -2x<6 \rightarrow\;\; -2x/-2>6/-2 \rightarrow x>-3$$

حال با در نظر گرفتن هر دو جواب، پاسخ نهایی به صورت زیر نوشته می‌شود:

$$-3$$

تعیین علامت عبارت‌های جبری

حال که قادر به حل نامساوی‌ها هستیم، می‌توانیم عبارت‌هایی جبری را نیز تعیین علامت کنیم. البته در مرحله اول، عبارت‌های مورد نظر ما از ضرب یا تقسیم چند جمله‌هایی مرتبه ۱ ساخته شده‌اند.

تعیین علامت یا حل نامساوی‌ها بسیار شبیه به حل معادلات یا تساوی‌ها است. با این تفاوت که برای پاسخ دادن به مسئله تعیین علامت یا نامساوی به مجموعه‌ای از مقدارها یا فاصله‌ای از اعداد حقیقی خواهیم رسید. بنابراین روال حل چنین مسئله‌هایی به صورت زیر نوشته می‌شود:

• پیدا کردن ریشه یا ریشه‌های معادله یا تساوی حاصل از چند جمله‌ای‌ها
• تعیین نقاط مجانبی یا مقدارهایی از متغیر x که به ازاء آن‌ها تساوی یا معادله تعریف نشده است.
• استفاده از یک محک برای تعیین مثبت با منفی بودن عبارت جبری

برای مشخص شدن این موضوع و انجام روال محاسبات مربوط به تعیین علامت عبارت جبری به مثال زیر توجه کنید.

مثال: نامساوی $$(x+2)(x-3)<0$$ را حل کنید.

مشخص است که برای آنکه حاصلضرب این دو پرانتز منفی باشد، باید یکی از آنها منفی باشند. بنابراین مسئله به تعیین علامت هر یک از عبارت‌ها شکسته می‌شود. هر یک از حالات را می‌نویسیم. ابتدا فرض می کنید که اولین عبارت منفی و دومین عبارت مثبت است. بعنی داشته باشیم:

$$(x+2)<0\; و\; (x-3)>0$$

سپس فرض می‌کنیم که اولین عبارت مثبت و دومین عبارت منفی است. بنابراین می‌نویسیم:

$$(x+2)>0\; و\; (x-3)<0$$

حالت اول:

$$x+2<0\rightarrow x+2-2<0-2\rightarrow x<-2$$

$$x-3>0\rightarrow x-3+3>0+3\rightarrow x>3$$

پس زمانی که x<-2 و x>3 باشد، حاصلضرب دو عبارت منفی است.

حالت دوم:

$$x+2>0\rightarrow x+2-2>0-2\rightarrow x>-2$$

$$x-3<0\rightarrow x-3+3<0+3\rightarrow x<3$$

پس زمانی که x>-2 و x<3 باشد، حاصلضرب دو عبارت باز هم منفی است. حال این دو حالت را بوسیله یک جدول، مقایسه می‌کنیم.

سطر آخر این جدول براساس حاصلضرب نتایج منفی و مثبت نوشته شده است و از قاعده معروف «منفی در منفی، مثبت» و همچنین «منفی در مثبت،‌ منفی» در آن استفاده شده است.

از آنجایی که به دنبال مقدارهایی می‌گشتیم که عبارت $$(x+2)(x-3)$$ منفی باشد، مشخص است ناحیه جواب به صورت زیر خواهد بود:

$$x>-2 , x<3 \rightarrow -2$$

از طرف دیگر اگر این دو عبارت را در یکدیگر ضرب کنیم به یک چند جمله‌ای درجه ۲ خواهیم رسید که به صورت $$x^2-x-6$$ نوشته می‌شود. منحنی رسم شده برای این چند جمله‌ای به صورت زیر است:

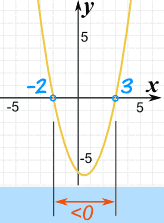
کاملا مشخص است که اگر $$-2$$ باشد، این چند جمله‌ای منفی است و منحنی مربوط به آن زیر محور افقی قرار می‌گیرد.

مثال: پاسخ نامساوی $$\frac{(x-2)}{(x-4)}>0$$ را بدست آورید.

از آنجایی که منفی یا مثبت بودن x-4 مشخص نیست، نمی‌توان با ضرب کردن دو طرف نامساوی روش حال معمول برای نامساوی را دنبال کرد. پس بهتر است ابتدا صورت و مخرج را تعیین علامت کنیم و سپس به مانند جدول بالا به تعیین علامت کل عبارت بپردازیم.

برای تعیین علامت نیز به همان شیوه قبل عمل می‌کنیم. برای آنکه حاصل کسر مثبت باشد باید یا هر دو عبارت صورت و مخرج مثبت یا هر دو منفی باشند.

حالت اول:

$$x-2>0 , x-4>0$$

در این حالت هر دو عبارت را تعیین علامت می‌کنیم.

$$x-2>0 \rightarrow x-2+2>0+2 \rightarrow x>2 \rightarrow x<2$$

همینطور

$$x-۴>0 \rightarrow x-۴+۴>0+۴ \rightarrow x>۴$$

حالت دوم:

$$x-2<0 , x-4<0$$

در این حالت هر دو عبارت را تعیین علامت می‌کنیم.

$$x-2<0 \rightarrow x-2+2<0+2 \rightarrow x<2$$

همینطور

$$x-۴<0 \rightarrow x-۴+۴<0+۴ \rightarrow x<۴$$

حال جدول را برای تعیین علامت جمله اصلی و حل نامساوی ترسیم می‌کنیم.

از آنجایی که اگر x=4 باشد، مخرج کسر برابر با صفر می شود، عبارت کسری نامعین می‌شود. این حالت را با نوشتن نامعین برای ریشه مخرج در جدول نشان داده‌ایم. این نقطه یعنی x=4 همان نقطه مجانبی است. در نهایت جواب برای این نامساوی به صورت فاصله $$(-\infty , 2)$$ یا $$(4,+\infty)$$ نوشته می‌شود.

نمودار این رابطه در زیر ترسیم شده است. همانطور که دیده می‌شود منحنی در نقطه x=2 محور افقی را قطع می‌کند پس این نقطه ریشه است. تا قبل از ریشه صورت و مخرج کسر مثبت هستند. از ریشه صورت تا ریشه مخرج نیز کسر منفی است زیرا صورت منفی و مخرج مثبت است. زمانی که به نقطه ریشه مخرج نزدیک می‌شویم، منحنی دارای یک مجانب عمودی می‌شود که به سمت منفی بی‌نهایت می‌رود. یعنی در این فاصله منفی است. بعد از ریشه مخرج (یعنی مقدار x=4) منحنی از مثبت بی‌نهایت شروع شده و کاهش پیدا می‌کند ولی همواره مثبت است زیرا در این فاصله هم صورت و هم مخرج کسر مثبت هستند.

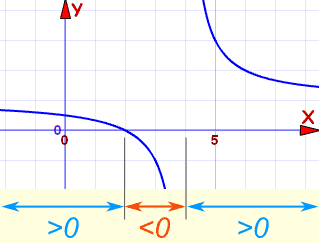
مثال: نامساوی $$\dfrac{(3x-10)}{(x-4)}>2$$ را حل کنید.

تا اینجا به بررسی نامساوی‌هایی پرداختیم که مثبت یا منفی بودن آن‌ها، مورد نظر بود. ولی این جا می‌خواهیم یک عبارت را با مقدار ۲ مقایسه کنیم. ابتدا باید عبارت بالا را ساده کنیم. بهتر است ۲ را به طرف دیگر نامساوی ببریم تا عبارت‌ها، چهره‌ای آشناتر پیدا کنند.

$$(3x-10)/(x-4)-2>0$$

سپس با ضرب و تقسیم کردن $$(x-4)$$ در ۲، عبارت ساده‌تر خواهد شد.

$$\dfrac{(3x-10)}{(x-4)}-2\dfrac{(x-4)}{(x-4)}> 0$$

$$\dfrac{(3x-10)}{(x-4)}-\dfrac{(2x-8)}{(x-4)}>0$$

حال صورت کسر را به شکل ساده‌تری می‌نویسیم.

$$\dfrac{(۳x-۲x-10+8)}{(x-4)}>0$$

$$\dfrac{(x-2)}{(x-4)}>0$$

همانطور که دیده می‌شود این عبارت مطابق مثال قبل می‌تواند تعیین علامت شود و ناحیه پاسخ برای نامساوی این مثال، مطابق با همان مثال قبل است.

ناحیه پاسخ برای نامساوی براساس چند جمله‌ای درجه ۲

همانطور که می‌دانید، یک چند جمله‌ای درجه ۲ به فرم $$ax^2+bx+c$$ نوشته می‌شود. البته با فرض اینکه $$a\neq0$$. حال به بررسی نامساوی‌هایی می‌پردازیم که ممکن است به فرم $$ax^2+bx+c>0$$ یا $$ax^2+bx+c<0$$ نوشته شوند. در اینجا هم برای پیدا کردن ناحیه جواب ابتدا ریشه‌های چندجمله‌ای را تعیین می‌کنیم.

فیلم آموزش برنامه نویسی متلب برای علوم و مهندسی در فرادرس

کلیک کنید

همانطور که در مطلب وبلاگ فرادرس با عنوان معادله درجه دو — به زبان ساده بیان شده است، برای پیدا کردن ریشه معادلات درجه ۲ باید از دلتا یا $$\Delta$$ و تعیین علامت آن استفاده کنیم.  در اینجا هم به همین شکل ناحیه پاسخ برای نامساوی برمبنای چندجمله‌ای را برحسب $$\Delta$$ تعیین می‌کنیم.

یادآوری می‌کنیم که دلتا به کمک رابطه زیر محاسبه می‌شود:

$$\Delta=b^2-4ac$$

جدول زیر به درک به کارگیری $$\Delta$$ برای تعیین علامت و حل نامساوی‌های چند جمله‌ای درجه ۲ کمک می‌کند.

 مثال: چند جمله‌ای $$x^2-x-6$$ را تعیین علامت کنید.

برای تعیین نواحی که این چند جمله‌ای منفی، مثبت یا صفر است، کافی است $$\Delta$$ و ریشه‌ها را بدست آوریم. بنابراین خواهیم داشت:

$$a=1, b=-1, c=-6$$

 با انجام محاسبات متوجه می‌شویم که مقدار دلتا برابر است با $$\Delta=(-1)^2-4(1)(-6)=1+24=25>0$$ در نتیجه برای چنین معادله‌ای دو ریشه حقیقی وجود دارد. از طرفی می‌توانیم مقدار ریشه‌ها را نیز محاسبه کنیم.

$$x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-(-1)+\sqrt{25}}{2(1)}=\dfrac{1+5}{2}=\frac{6}{2}=3$$

$$x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-(-1)-\sqrt{25}}{2(1)}=\dfrac{1-5}{2}=\frac{-4}{2}=-2$$

پس می‌توان طبق جدول زیر چند جمله‌ای  $$x^2-x-6$$ را تعیین علامت کرد.

همانطور که دیده می‌شود بین دو ریشه یعنی فاصله $$(-2,3)$$ عبارت چند جمله‌ای، منفی، یعنی مخالف علامت a است و در ناحیه خارج از دو ریشه موافق علامت a (مثبت) است.