احتمال شرطی (Conditional Probability) — اصول و شیوه محاسبه

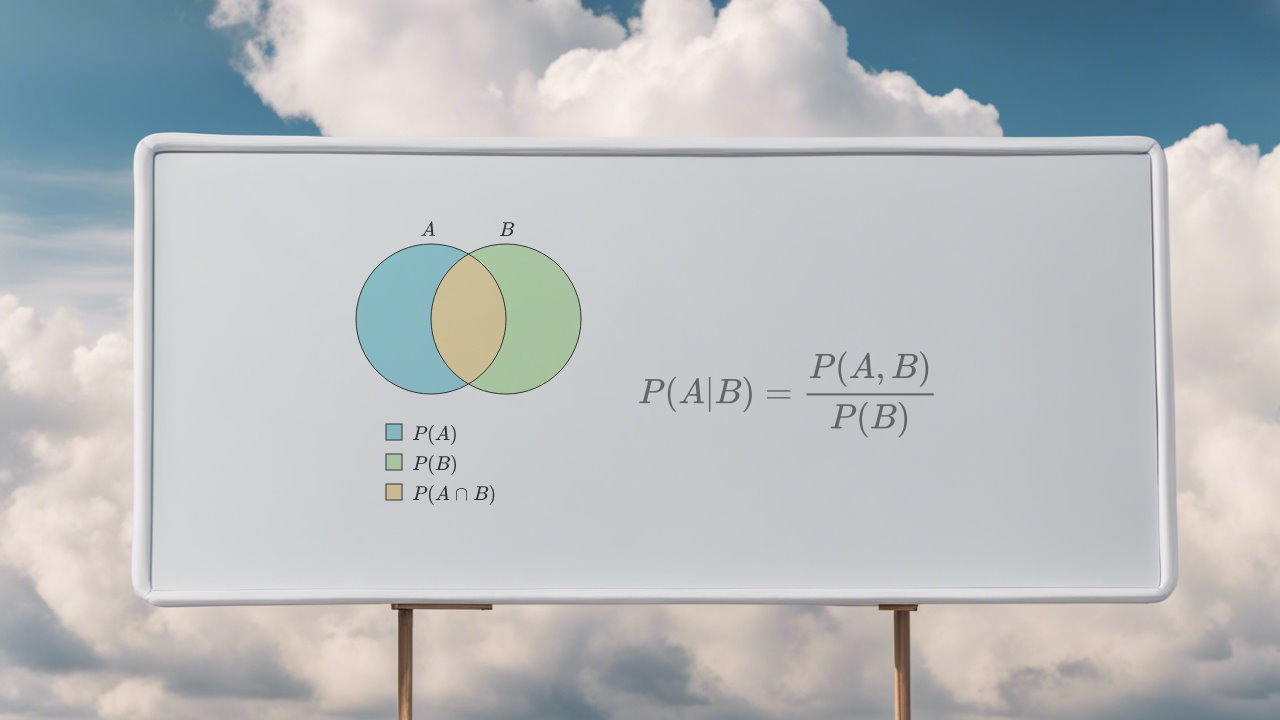
در مبحث احتمال، وقوع یا عدم وقوع یک پیشامد، می‌تواند در رخداد پیشامدهای دیگر تاثیرگذار باشد. به این ترتیب ممکن است احتمال رخداد پیشامد A تحت تاثیر رخداد پیشامد B کاهش یا افزایش یابد. برای مثال، ممکن است اطلاع از ابری بودن آسمان در فردا، احتمال بارندگی در صبح فردا را افزایش دهد. پس لازم است ارتباط و تاثیر دو پیشامد بریکدیگر را برای محاسبه احتمال هر یک مشخص کنیم. در چنین حالتی بحث احتمال شرطی (Conditional Probability) بوجود می‌آید.

فرض کنید سکه‌ای را دو بار پرتاب کرده‌ایم. فضای نمونه برای این آزمایش تصادفی به صورت $$\Omega=\{HH,HT,TH,TT\}$$ است. بنابراین با توجه به فضای نمونه $$\Omega$$، پیشامد مشاهده حداقل یک شیر، برابر است با:

$$A=\{HH,TH,HT\}$$

اگر براساس مفهوم احتمال به کمک فراوانی نسبی بخواهیم احتمال پیشامد A را محاسبه کنیم، کافی است نسبت تعداد اعضای پیشامد A را به تعداد اعضای فضای نمونه تقسیم کنیم. به این ترتیب مقدار احتمال برابر خواهد بود با:

$$P(A)=\dfrac{|A|}{|\Omega|}=\dfrac{3}{4}$$

حال فرض کنید از قبل می‌دانیم که سکه اول شیر آمده است. در نتیجه فضای نمونه به  $$\Omega=\{HH,HT\}$$ تقلیل پیدا می‌کند. اکنون پیشامد مشاهده حداقل یک شیر برابر است $$A=\{HH,HT\}$$  و احتمال آن برابر خواهد بود با:

$$P(A)=\dfrac{|A|}{|\Omega|}=\dfrac{۲}{۲}=۱$$

همانطور که دیده می‌شود، آگاهی از یک پیشامد می‌تواند مقدار احتمال برای پیشامد دیگر را تغییر دهد. برای اطلاع از مباحث مربوط به تابع احتمال بهتر است ابتدا مطلب آزمایش تصادفی، پیشامد و تابع احتمال را مطالعه کنید.

احتمال شرطی

فرض کنید پیشامد B با احتمال مثبت رخ داده است. احتمال پیشامد A به شرط B را به صورت $$P(A|B)$$ می‌نویسیم و می‌خوانیم احتمال A به شرط B. این احتمال به صورت زیر تعریف می‌شود.

$$P(A|B)=\dfrac{P(A\cap B)}{P(B)};\;\;\;\ P(B)>0$$

فیلم آموزش آمار و احتمال – پایه یازدهم

اینجا کلیک کنید

با توجه به این تعریف، اگر P(B)=0، احتمال شرطی تعریف نشده است.

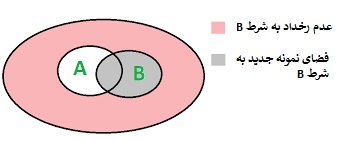
همانطور که در تصویر دیده می‌شود، به نظر می‌رسد، با اطلاع از وقوع پیشامد B، فضای نمونه از $$\Omega$$ به B تقلیل پیدا کرده است و احتمال پیشامد A باید براساس فضای نمونه جدید محاسبه شود.

می‌توان نشان داد که احتمال شرطی نیز یک تابع احتمال است. یعنی در اصول تابع احتمال که توسط کولموگروف معرفی شد، صدق می‌کند. گفتنی است که اصول احتمال در مطلب آزمایش تصادفی، پیشامد و تابع احتمال معرفی شده‌اند.

برای نشان دادن موضوع یاد شده این اصول را برای احتمال شرطی بررسی می‌کنیم:

اصل اول- احتمال شرطی نامنفی است. بنا به تعریف احتمال شرطی، مشخص است که در رابطه ذکر شده، مخرج نامنفی و صورت نیز نامنفی است. در نتیجه نسبت این دو قسمت نیز نامنفی خواهد بود.

اصل دوم- مقدار احتمال شرطی برای فضای نمونه باید برابر با ۱ باشد. یعنی:

$$P(\Omega |B)=\dfrac{P(\Omega \cap B)}{P(B)}=\dfrac{P(B)}{P(B)}=1$$

زیرا می‌دانیم که $$B\subset \Omega$$. پس $$\Omega \cap B= B$$.

اصل سوم- احتمال شرطی اجتماع هر دنباله از پیشامدهای دو به دو ناسازگار، برابر با مجموع احتمال شرطی پیشامدهای این دنباله است. یعنی باید نشان دهیم که:

$$P(\cup_{i=1}^\infty A_i|B)= \sum_{i=1}^\infty P(A_i|B)$$

براساس تعریف احتمال شرطی می‌توان نوشت:

$$P(\cup_{i=1}^\infty A_i|B)=\dfrac{P((\cup_{i=1}^\infty A_i)\cap B)}{P(B)}=\dfrac{P(\cup_{i=1}^\infty (A_i\cap B))}{P(B)}$$

چون $$A_i$$ها دو به دو ناسازگار هستند پس اشتراکشان با B نیز دو به دو ناسازگار است. یعنی $$(A_i\cap B) \cap (A_j\cap B)=(A_i\cap A_j)\cap B=\emptyset$$. در نتیجه خواهیم داشت:

$$\dfrac{P(\cup_{i=1}^\infty (A_i\cap B))}{P(B)}=\dfrac{\sum_{i=1}^\infty P(A_i\cap B)}{P(B)}=$$

$$\sum_{i=1}^\infty \dfrac{P(A_i\cap B)}{P(B)}$$

که درنهایت برابر است با:

$$\sum_{i=1}^\infty {P(A_i|B)}$$

به این ترتیب نشان دادیم که تابع احتمال شرطی، در اصول احتمال صدق می‌کند.

مثال ۱

دو تاس نااریب را پرتاب کرده‌ایم. متوجه شده‌ایم که جفت ظاهر شده است. احتمال اینکه هر دو عدد‌ ۶ باشند به صورت زیر محاسبه می‌شود:

در چنین حالتی فضای نمونه به صورت $$\Omega=\{(x,y);x=1,2,\ldots,6; y=1,2,\ldots,6\}$$ است.

فرض کنید که A‌ پیشامد مشاهده عدد شش در یکی از تاس‌ها باشد. همچنین پیشامد مشاهده جفت را نیز با B نشان دهیم:

$$A=\{(1,6),(6,1),(2,6),(6,2),(3,6),(6,3),(4,6),(6,4),(5,6),(6,5),(6,6)\}$$

$$B=\{(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)\}$$

پس $$A\cap B = \{(6,6)\}$$. در نتیجه مقدار احتمال شرطی $$P(A|B)$$ به صورت زیر محاسبه می‌شود:

$$P(A|B)=\dfrac{P(A \cap B)}{P(B)}=\dfrac{\dfrac{1}{36}}{\dfrac{6}{36}}=\dfrac{1}{6}$$

در حالیکه اگر بدون شرط B احتمال A را محاسبه کنیم خواهیم داشت:

$$P(A)=\dfrac{11}{36}>P(A|B)=\dfrac{1}{6}$$

این مسئله نشان می‌دهد که آگاهی از پیشامد B احتمال رخداد پیشامد A را کاهش داده‌ است.

قانون ضرب احتمال

اگر طرفین رابطه احتمال شرطی را در یکدیگر ضرب کنیم، رابطه‌ای به صورت زیر حاصل می‌شود:

$$P(A\cap B)=P(A|B)P(B)$$

این رابطه به نام قانون ضرب احتمال معروف است.

مثال ۲

در یک کیوسک بانکی یک کولر گازی به همراه یک دستگاه خودپرداز کار می‌کند. احتمال اینکه کولر گازی خراب شود، برابر است با 10٪ و احتمال اینکه دستگاه خودپرداز در اثر گرمای زیاد (عدم کارکرد کولرگازی) از سرویس خارج شود، 50٪ است. احتمال اینکه هر دو خراب شوند به صورت زیر محاسبه می‌شود:

$$P(A\cap B)=P(A|B)P(B)=0.5\times 0.1=0.05$$

مثال ۳

برای آنکه $$P(A|B)=P(B|A)$$ باشد،‌ چه رابطه‌ای بین A و B باید وجود داشته باشد؟ (با فرض اینکه $$P(A)\neq 0$$ و $$P(B)\neq 0$$)

با توجه به تعریف احتمال شرطی، هر دو طرف تساوی را دوباره می‌نویسیم:

$$P(A|B)=\dfrac{P(A\cap B)}{P(B)},\;\;\;\; P(B|A)=\dfrac{P(B\cap B}{P(A)}$$

حال با مساوی قرار دادن دو رابطه اخیر خواهیم داشت:

$$\dfrac{P(A\cap B)}{P(B)}=\dfrac{P(B\cap A)}{P(A)}$$

از آنجایی که $$P(A\cap B)=P(B\cap A)$$، تساوی بالا زمانی برقرار است که $$P(A)=P(B)$$. پس در صورتی که $$P(A)=P(B)$$ می‌توان نوشت:  $$P(A|B)=P(B|A)$$

استقلال دو پیشامد

اگر در بحث احتمال شرطی، رخداد پیشامد B در احتمال رخداد پیشامد A هیچ تاثیری نداشته باشد، آنگاه پیشامد A را مستقل از B می‌گویند. در این حالت براساس رابطه شرطی می‌توان نوشت:

$$P(A|B)=P(A)$$

فیلم آموزش احتمال شرطی و پیشامد های مستقل در ریاضی ۲ – پایه یازدهم علوم تجربی (رایگان)

اینجا کلیک کنید

البته این رابطه را براساس قانون ضرب احتمال به صورت زیر نیز می‌توان نمایش داد:

$$P(A\cap B)=P(A)P(B)$$

مثال ۴

فرض کنید در پرتاب دو سکه پیشامد A را رخداد دو شیر در نظر بگیریم و B‌ نیز رخداد دو خط باشد. این دو پیشامد ناسازگار هستند ولی از هم مستقل نیستند، زیرا:

$$P(A\cap B)=P(\emptyset)=0\neq P(A)P(B)=\dfrac{1}{4}\times \dfrac{1}{4}=\dfrac{1}{16}$$

اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزش‌هایی که در ادامه آمده‌اند نیز برایتان کاربردی خواهند بود.

• مجموعه آموزش های برنامه نویسی متلب برای علوم و مهندسی
• متغیر های تصادفی – میانگین، واریانس و انحراف معیار – به زبان ساده
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش آمار و احتمال مهندسی
• آزمایش تصادفی، پیشامد و تابع احتمال

^^