ضرب خارجی بردارها – به زبان ساده

در مطالب گذشته مجله فرادرس، مفاهیم مربوط به بردارها را مطرح کردیم. هم‌چنین در مطلبی مجزا، نحوه بدست آوردن ضرب داخلی دو بردار را توضیح دادیم. در این قسمت قصد داریم تا نوع دیگری از ضرب دو بردار را بررسی کنیم.

تعریف ضرب خارجی

ضرب خارجی، به عملیاتی در ریاضیات گفته می‌شود که با استفاده از آن می‌توان دو بردار را در فضایی دو یا چند بعدی در هم ضرب کرد. بر خلاف ضرب داخلی، حاصل این نوع ضرب، کمیتی برداری خواهد بود.

ضرب خارجی دو بردار a و b را به صورت زیر نشان می‌دهند.

a×b = ضرب خارجی دو بردار a و b

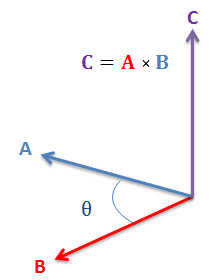
مطابق شکل بالا حاصل‌ضرب خارجی دو بردار a و b در یکدیگر، بر هر دوی آن‌ها عمود شده است.

محاسبه ضرب خارجی

همانند شکل زیر دو بردار a و b را تصور کنید.

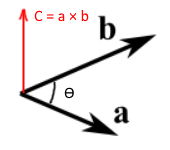
حاصلضرب خارجی این دو بردار برابر با مقدار زیر است.

فیلم آموزش ریاضی عمومی 2 – جامع و کاربردی در فرادرس

کلیک کنید

در این معادله |a| و |b| به ترتیب برابر با اندازه‌های بردار a و b هستند. همچنین $$\theta$$، زاویه بین این دو بردار است. بایستی توجه داشته باشید که n، بردار واحد است که بر هر دو بردار اولیه (a و b) عمود شده. بنابراین جهت این بردار در راستای n و اندازه آن برابر با حاصلضرب اندازه a در b در سینوس زاویه بین آن‌ها است.

اگر بردارهای a و b در دستگاه مختصات کارتزینی و به صورت $$a=(a_x,a_y,a_z)$$ و $$b=(b_x,b_y,b_z)$$ بیان شوند، حاصل‌ضرب خارجی را می‌توان به شکل محاسبه کرد.

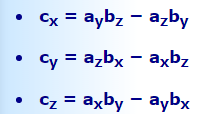
معادلات بالا در حقیقت دترمینان یک ماتریس هستند. به منظور درک بهتر، دو بردار $$a=(a_1,a_2,a_3)$$ و $$b=(b_1,b_2,b_3)$$ را در نظر بگیرید. همان‌طور که در بالا نیز بیان شد حاصل‌ضرب خارجی دو بردار، کمیتی برداری است؛ برای محاسبه حاصل‌ضرب خارجی این دو بردار می‌توان از دترمینان ماتریس زیر استفاده کرد.

$$\begin{aligned} \overrightarrow{\mathbf{c}} &=\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}=\left|\begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{array}\right|=\\ &=\left(a_{2} b_{3}-a_{3} b_{2}\right) \overrightarrow{\mathbf{i}}+\left(a_{3} b_{1}-a_{1} b_{3}\right) \overrightarrow{\mathbf{j}}+\left(a_{1} b_{2}-a_{2} b_{1}\right) \overrightarrow{\mathbf{k}} \end{aligned}$$

توجه داشته باشید که سطر اول این ماتریس حاوی بردارهای واحد در سه جهت مختصاتی است $$({\overrightarrow i},{\overrightarrow j},{\overrightarrow k})$$.

مثال

حاصلضرب خارجی دو بردار (۲,۳,۴)=a و (5,6,7)=b را بیابید. با توجه به فرمول بالا می‌توان گفت:

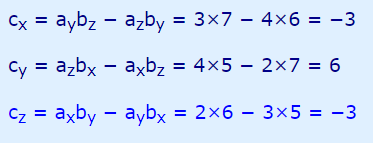
بنابراین با محاسبه عبارات بالا، پاسخ مد نظر برابر با مقدار زیر است.

$$\large a×b=(-3,6,-3)$$

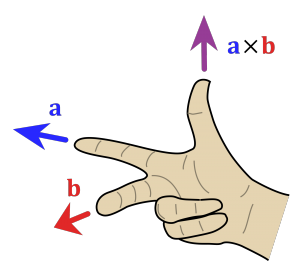
جهت بردار حاصل از یک ضرب خارجی

برای تعیین جهت پاسخ ضرب خارجی یک بردار می‌توان مطابق با شکل زیر از قانون دست‌ راست استفاده کرد. در حقیت در این روش انگشتان دست راست را در راستای بردار a قرار داده و سپس انگشت وسط را به سمت بردار b می‌چرخانیم. در این حالت جهت شست دست، بردار a×b را نشان می‌دهد. در شکل زیر این قانون تشریح شده.