ضرب داخلی بردارها — به زبان ساده

پیشتر در وبلاگ فرادرس، مفهوم اساسی بردارها را معرفی کردیم. در قسمتی از مطلب مذکور در مورد نحوه انجام اعمال ریاضی روی آنها بحث شد. در این مطلب قصد داریم تا یکی از روشهای ضرب بردارها، تحت عنوان «ضرب داخلی» را مورد توجه قرار دهیم.
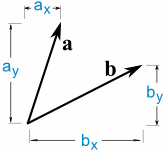
بردار، کمیتی است که دارای اندازه و جهت است. در شکل زیر دو بردار را میبینید.

این دو بردار را میتوان با استفاده از ضرب داخلی در یکدیگر ضرب کرد.
ضرب داخلی به چه معنا است؟
حاصل ضرب داخلیِ دو بردار که به صورت زیر نشان داده میشود، یک عدد اسکالر است.
a · b
این عبارت به صورت «حاصل ضرب داخلی بردار a در بردار b» خوانده میشود. مقدار این حاصلضرب با استفاده از فرمول زیر محاسبه میشود.
(a · b = |a| × |b| × cos(θ
اجزاء این فرمول به ترتیب زیر هستند:
|a|: اندازه (طول) بردار a
|b|: اندازه (طول) بردار b
θ: زاویه بین بردار a و b
بنابراین بهمنظور محاسبه ضرب داخلی، ابتدا اندازه دو بردار a و b، در یکدیگر ضرب شده، سپس مقدار بدست آمده، در کسینوس زاویه بین دو بردار ضرب میشود.
اگر بردارهای مذکور در مختصات کارتزینی بیان شده باشند [(a=(ax,ay و (b=(bx,by]، ضرب داخلی را میتوان بهصورت زیر نوشت.
a · b = (ax × bx) + (ay × by)
بنابراین مولفههای x دو بردار در یکدیگر و مولفههای y آنها نیز در هم ضرب شده و نهایتا با یکدیگر جمع میشوند.
مثال ۱
ضرب داخلی دو بردار a و b را که در شکل زیر آمده، محاسبه کنید.
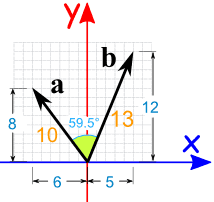
روش اول: با استفاده از معادله (a · b = |a| × |b| × cos(θ و جایگذاری کردن اندازه بردارهای مفروض در این معادله، داریم:
a · b = 10 × 13 × cos(59.5°)
a · b = 10 × 13 × 0.5075...
a · b = 65.98... = 66 (گرد شده)
روش دوم: میتوان مولفههای دو بردار مفروض را در معادله (a · b = (ax × bx) + (ay × by قرار داد. بنابراین داریم:
a · b = -6 × 5 + 8 × 12
a · b = -30 + 96
a · b = 66
توجه داشته باشید که ax منفی در نظر گرفته شده، چراکه جهت آن خلاف جهتِ مثبتِ محور x است. همانطور که میبینید مقدار بدست آمده در بالا یک عدد است. بنابراین بر خلاف ضرب خارجی دو بردار، حاصل ضرب داخلی عددی اسکالر (نردهای) است.
چرا (Cos (θ ؟
اگر دو بردار در یک راستا باشند، ضرب داخلی آنها در واقع همان ضرب طولشان است؛ بنابراین ضرب دو بردار در چنین شرایطی قابل درک است. در نتیجه بهمنظور انجام ضرب داخلی تحت هر شرایطی، دو بردار را بایستی در یک جهت قرار داد.
در حقیقت ضرب داخلی، معادل با ضرب طول تصویر شده یکی از بردارها در طول دیگری است.
همچنین برای تصویر کردن یک بردار روی برداری دیگر، بایستی بردار اول را در Cos زاویه بینشان ضرب کرد.

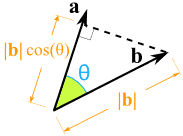
همانطور که در دو شکل بالا دیده میشود، حاصلضرب طول تصویر شده هر کدام از بردارها در طول دیگری برابر است با:
|a| × |b| × cos(θ) = |a| × cos(θ) × |b|
همانطور که میبینید معادله حاصل شده، همان ضرب داخلی است که در دو حالتِ تصویر شده، با یکدیگر برابر هستند.
دو بردار عمود بر هم
ضرب داخلی دو بردار عمود بر هم، صفر است.
مثال ۲
ضرب داخلی دو بردار شکل زیر را محاسبه کنید.
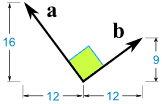
a · b = |a| × |b| × cos(90°)
a · b = |a| × |b| × 0
a · b = 0
و یا با استفاده از روش دوم میتوان بیان کرد:
a · b = -12 × 12 + 16 × 9
a · b = -144 + 144
a · b = 0
همانطور که میبینید ضرب داخلی دو بردار عمود بر هم، صفر است.
ضرب داخلی بردارها در ابعاد بالاتر
بهمنظور محاسبه ضرب داخلی در سه یا چند بعد، مشابه با روشهای بیان شده در بالا عمل میشود.
مثال ۳
زاویه میان دو بردار رسم شده در شکل زیر را بیابید.
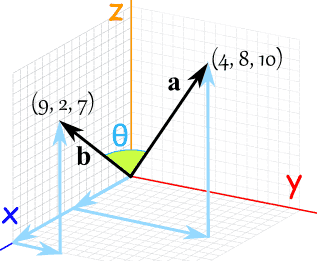
در این مثال مولفه z نیز وجود دارد، بنابراین بایستی تاثیر آن را هم در نظر گرفت. در واقع در این حالت، فرمول ضرب داخلی به صورت a · b = ax × bx + ay × by + az × bz در نظر گرفته میشود. بنابراین با جایگذاری مولفههای بردارها در این فرمول خواهیم داشت:
a · b = 9 × 4 + 2 × 8 + 7 × 10
a · b = 36 + 16 + 70
a · b = 122
از طرفی با استفاده از فرمول (a.b=|a| × |b| × cos(θ نیز می توان ضرب داخلی را حساب کرد. ولی قبل از محاسبه، بایستی اندازه دو بردار مفروض، محاسبه شوند. بنابراین مطابق با قانون فیثاغورث نتیجه میشود:
بر همین مبنا اندازه بردار b برابر است با:
از طرفی در بالا نیز مقدار a.b برابر با ۱۲۲ محاسبه شد. با جایگذاری این مقدار و اندازههای بردار a و b در فرمول (a.b=|a| × |b| × cos(θ، کسینوس زاویه بین دو بردار بهصورت زیر محاسبه میشود.
122 = √180 × √134 × cos(θ)
cos(θ) = 122 / (√180 × √134)
cos(θ) = 0.7855...
θ = cos-1(0.7855) = 38.2°
در مطلب آینده در مورد نوع دیگری از ضرب بردارها، تحت عنوان ضرب خارجی را توضیح خواهیم داد.
در صورتی که به مباحث مرتبط در زمینه ریاضیات پایه علاقهمند هستید، احتمالا میتوانید از آموزشهای زیر استفاده کنید.
- مجموعه آموزشی دروس دبیرستان
- مجموعه آموزشهای ریاضی و فیزیک
- بردار و اسکالر -- به زبان ساده
- علائم هندسی در ریاضیات — به زبان ساده
- مجموعه ها در ریاضیات – مفاهیم پایه
^^













خیلی کامل و مفید بود خیلی ممنون
درود
سپاس فراوان از روان و ساده بودن شیوه آموزش . فقط اگر با ذکر مثال بین سه بردار را هم کامل تر توضیح میدادید دیگه بی نظیر میشد. بازم سپاس
سلام و عرض خسته نباشید خدمت شما
خیلییی عالی و مختصر و مفید بود
دستتون درد نکنه
ایول دمت گرم توضیحات خیلی عالی وقابل فهم بود
خیلی مفید بود
خیلی عالی بود
بسیار آموزنده ومفید بود.🌹
اوکی
مفهوم این جمله چیست؟ضرب داخلی دو بردار عمود بر هم، صفر است
سلام و روز شما به خیر؛
جمله مد نظر شما به این معنی است که اگر دو بردار a و b با یکدیگر زاویه 90 درجه بسازند، حاصل a.b برابر با صفر میشود.
از همراهی شما با فرادرس خرسندیم.
سلام
این اموزش کوتاه
خیلی بهتر از اموزش فیزیک ۱ فرادرس بود
بسیار عالی و مفید بود سپاسگزارم.
با سلام و تشکر
کارکرد ضرب داخلی بردار چیست؟
عالی بود خیلی ممنون من چند ساله بین لیسانسو و فوق لیسانسم فاصله افتاده وبلاگ شما خیلی در یاداوری چیزایی که یادم رفته موثر بود متشکرم
سلام این بخش نفهمیدیم cos(θ) = 122 / (√180 × √134) یه توضیح کوچیک میدین مشکلم این حساب √180 × √1۳۴
شکل مثال سه فکر نمیکنم ابعاد بالاتر رو نشون بده لطفا چک کنین
سلام.
تصویر صحیح جایگزین شد.
از توجه شما سپاسگزاریم.
ممنون از مطالب مفیدتون