بردار ویژه و مقدار ویژه — از صفر تا صد

در این مطلب از مجله فرادرس در مورد بردار ویژه و مقدار ویژه به طور کامل صحبت می‌کنیم. مقدار ویژه و بردار ویژه، از مباحث مهم و کاربردی جبر خطی است که کاربردهای مختلفی در مباحث گوناگون ریاضیات، فیزیک، مکانیک، عمران، برق و... مانند دینامیک سیالات محاسباتی، تئوری الاستیسیته، علم داده‌ها و یادگیری ماشین و سیستم‌های کنترل دارد.

یک ماتریس مربعی $$3\times3$$ را در نظر بگیرید که در یک بردار $$3\times1$$ ضرب می‌شود. نتیجه، یک بردار $$3\times 1$$ است. ماتریس $$3\times 3$$ موردنظر را می‌توان به‌عنوان یک اپراتور یا عملگر درنظر گرفت که به بردار اعمال می‌شود و بردار جدیدی را می‌سازد. نمونه‌های زیادی در ریاضیات و فیزیک وجود دارد که می‌خواهیم بردار با اعمال ماتریس ذاتاً بدون تغییر باقی بماند.

به طور خاص، می‌خواهیم بردار v در رابطه $$Av=\lambda v$$‌ صدق کند که A یک ماتریس مربعی و $$\lambda$$ یک عدد حقیقی است. بردار v که در این معادله صدق می‌کند، «بردار ویژه» (Eigenvector) ماتریس A و ثابت $$\lambda$$، «مقدار ویژه» (Eigenvalue) یا مقدار مشخصه (Characteristic value) نامیده می‌شود.

فیلم آموزش ریاضی فیزیک ۱ در فرادرس

کلیک کنید

از نظر هندسی، اعمال (ضرب) یک ماتریس در یکی از بردار ویژه‌هایش، سبب بزرگ، کوچک و یا معکوس شدن جهت آن می‌شود.

برای یافتن مقادیر ویژه ماتریس A با ابعاد $$n\times n$$، باید معادله $$Av=\lambda v$$ را برای اسکالر(های) $$\lambda$$ حل کنیم. با کمی جابه‌جایی معادله، داریم: $$Av-\lambda v=0$$. می‌توانیم رابطه $$\lambda v=\lambda Iv$$ را نیز بنویسیم که در آن، I یک ماتریس یکه یا همانی $$n\times n$$ است:

بنابراین،

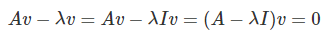
این معادله، یک سیستم همگن با n معادله و n مجهول است. معادله فوق، یک حل غیرصفر برای v دارد، اگر و فقط اگر دترمینان $$(A-\lambda I)$$ صفر باشد. بنابراین، با یافتن ریشه‌های چندجمله‌ای $$\lambda$$ از معادله مشخصه (characteristic equation) $$det(A-\lambda I)=0$$، می‌توان مقادیر ویژه ماتریس A را به دست آورد.

مثال زیر، نحوه محاسبه مقادیر و بردارهای ویژه‌ و برخی از اصطلاحات مربوط به آن‌ها را بیان می‌کند.

مثال 1

ماتریس A را در نظر بگیرید:

فیلم آموزش جبر خطی – مرور و حل مساله در فرادرس

کلیک کنید

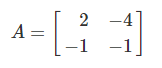
معادله مشخصه ($$p(\lambda)$$) این ماتریس، به‌صورت زیر است:

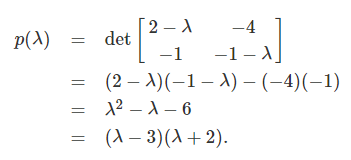
در نتیجه، $$\lambda _1=3$$ و $$\lambda _2=-2$$، مقادیر ویژه ماتریس A هستند. برای پیدا کردن بردارهای ویژه متناظر با مقادیر ویژه $$\lambda$$، باید معادلات خطی زیر را حل کنیم:

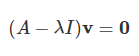
که در آن، v، ویژه متناظر با مقدار ویژه $$\lambda$$ است:

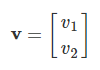
می‌خواهیم بردار ویژه متناظر با $$\lambda _1=3$$ را محاسبه کنیم. معادله $$(A-3I)v=0$$، به‌صورت زیر است:

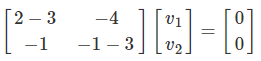
رابطه بالا، به دو معادله زیر می‌انجامد:

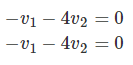
که با هم برابر هستند. بنابراین، اگر $$v_2=t$$ قرار دهیم، $$v_1=-4t$$ خواهد شد. تمام بردار ویژه‌های متناظر مقدار ویژه $$\lambda _1=3$$، از ضرایب بردار زیر هستند:

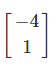
بنابراین، فضای ویژه (eigenspace) متناظر با $$\lambda _1=3$$، اسپن (Span) این بردار است. درنتیجه، بردار زیر، یک پایه (basis) برای فضای ویژه متناظر با $$\lambda _1=3$$ است.

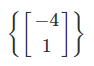
به‌طریق مشابه، یک پایه برای مقدار ویژه $$\lambda _2=-2$$، به‌شکل زیر است:

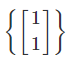
در ادامه، چند مثال دیگر بیان می‌شود که در آن‌ها، k نشان دهنده مقدار ویژه است.

مثال 2

برای یافتن مقادیر ویژه ماتریسِ زیر، آن را در معادله $$det(A-kI)=0$$ قرار داده و برای k حل می‌کنیم.

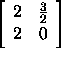
ماتریس $$A-kI$$ به صورت زیر است:

بنابراین، دترمینان آن برابر $$k^2-2k-3$$ خواهد بود. با حل این معادله درجه دو $$k^2-2k-3$$، مقادیر $$k=3$$ و $$k=-1$$ به‌دست می‌آید. برای یافتن بردارهای ویژه مربوط به مقدار ویژه $$k=3$$، باید v را از مجموعه معادلات $$(A-3I)v=0$$ به‌دست آورد:

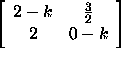
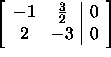
از آن‌جایی که معادله دوم، ضریبی از معادله اول است، این سیستم معادلات، به $$-x+(3/2)y=0$$ یا $$x=1.5y$$ کاهش می‌یابد. این معادله، بی‌نهایت حل دارد، برای مثال، با انتخاب y=2، بردار $$[3; 2]$$ به‌دست می‌آید که بردار ویژه مربوط به مقدار ویژه $$k=3$$ است. در حالت کلی، تمام بردار ویژه‌های متناظر با مقدار ویژه ۳، به‌شکل $$[3t ; 2t]$$ هستند که در آن، t یک عدد حقیقی دلخواه است. به‌طریق مشابه، بردارهای ویژه متناظر با مقدار ویژه $$k=-1$$ به‌صورت $$[-t ; 2t]$$ خواهند بود.

مثال 3

می‌خواهیم مقادیر ویژه و بردارهای ویژه ماتریس زیر را محاسبه کنیم:

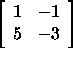
ابتدا، دترمینان $$A-kI$$ را به‌دست می‌آوریم:

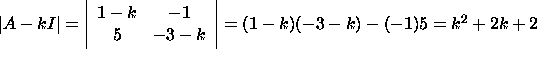
معادله مشخصه، دو ریشه مختلط $$k=-1+i$$ و $$k=-1-i$$ دارد. برای یافتن بردار ویژه‌های $$k=-1+i$$، باید معادله $$(A-(-1+i)I)v=0$$‌ را برای v حل کنیم:

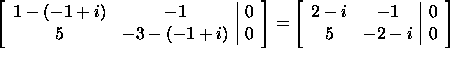
معادله دوم، ضریبی از معادله اول است، بنابراین، معادله $$(2i)x-y=0$$ یا معادل $$y=(2-i)x$$ را خواهیم داشت. در نتیجه، بردارهای ویژه ماتریس A برای مقدار ویژه $$k=-1+i$$ به‌شکل $$[t; (2-i)t]$$ است. به طریق مشابه، بردار ویژه $$[t; (2+i)t]$$، مربوط به مقدار ویژه $$k=-1-i$$ است.

با توجه به مثال‌های بالا، می‌توانیم یکی از ویژگی‌های مقادیر و بردارهای ویژه را معرفی کنیم. بردار ویژه‌های مقادیر ویژه مجزا، مستقل خطی هستند. مثال‌های زیر نشان می‌دهند این ویژگی هنگامی که مقادیر ویژه مجزا نباشند، با ابهام مواجه می‌شود.

مثال 4

ماتریس زیر، دو مقدار ویژه (۱ و 1) دارد که مجزا از هم نیستند.

فیلم آموزش ریاضی عمومی ۲ + حل مثال در فرادرس

کلیک کنید

از آن‌جایی که A یک ماتریس همانی است، برای هر بردار v داریم: $$Av=v$$، یعنی هر بردار دلخواهی می‌تواند بردار ویژه ماتریس A باشد. به‌عنوان مثال می‌توانیم دو بردار مستقل خطی $$[-2;1]$$ و $$[3;-2]$$ را برای هر کدام از مقادیر ویژه بنویسیم.

مثال 5

ماتریس زیر را در نظر بگیرید که مقادیر ویژه آن نیز 1 و 1 است.

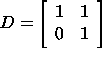
بردار ویژه‌های این ماتریس، از حل $$(A-I)v=0$$ به‌دست می‌آید که به فرم $$[t;0]$$ است. در نتیجه، دو بردار ویژه مستقل خطی برای دو مقدار ویژه 1 و 1 وجود ندارد.

محاسبه با متلب

با استفاده از دستور ساده eig در نرم‌افزار متلب می‌توان مقادیر و بردارهای ویژه یک ماتریس را به‌دست آورد:

فیلم آموزش جبر خطی با متلب در فرادرس

کلیک کنید

1>> A=[0 1;-2 -3]
2A =
3   0   1
4  -2  -3
5
6>> [v,d]=eig(A)
7v =
8   0.7071  -0.4472
9  -0.7071   0.8944
10  
11d =
12  -1   0
13   0  -2