فاکتوریل و اصول شمارش ترتیب و ترکیب – به زبان ساده

در این مطلب از مجله فرادرس با فاکتوریل و اصول شمارش ترتیب و ترکیب آشنا می‌شویم. به کمک «اصول شمارش» (Counting Rules)، می‌توانیم اعضای یک مجموعه را بشماریم. همچنین با کمک این اصول، محاسبات و مفاهیم دیگری مانند «فاکتوریل» (Factorial) شکل می‌گیرند که در انجام شمارش به ما یاری می‌رسانند. در این مطلب به معرفی اصول شمارش، پرداخته و سپس براساس آن‌ها به معرفی تابع فاکتوریل می‌پردازیم. این مفاهیم در محاسبات مربوط به «ترتیب» (Permutation) و «ترکیب» (Combination) که مرتبط به جایگشت‌ها است به کار گرفته می‌شود. در انتها نیز به کمک تابع گاما، مفهوم فاکتوریل را برای اعداد حقیقی معرفی خواهیم کرد.

اصول شمارش

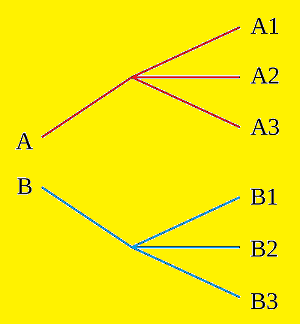
فرض کنید دو کار یا فعالیت به نام‌های A و B قرار است انجام شوند. عمل A به دو روش و عمل B به سه روش صورت می‌پذیرند. برای مثال فرض کنید که می خواهیم با استفاده از اعداد ۱ و ۲ و۳ همچنین حروف A و B ترکیبی دو بخشی از اعداد و حروف بسازیم که حتما با یک حرف شروع و با یک عدد نیز خاتمه یابند.

برای مشخص شدن تعداد حالت‌های ممکن، شاید لازم باشد که همه آن‌ها را بنویسیم.

$$Z=\{A1,A2,A3,B1,B2,B3\}$$

به این ترتیب مجموعه Z نتیجه همه حالت‌های قرارگیری حروف و اعداد در کنار یکدیگر است. ولی اگر تعداد اعداد و یا حروف زیاد باشند، در عمل نوشتن مجموعه‌ای که همه نوع ترکیبی را نشان دهد بسیار زمان‌بر خواهد بود و ممکن است که اشتباهی هم در نوشتن مجموعه Z رخ دهد. در نتیجه شمارش اعضای مجموعه Z دقیق نخواهد بود. یک راه حل مناسب برای این مسئله، استفاده از اصول و قواعد شمارش است. با توجه به این موضوع، به بررسی دو اصل مربوط به شمارش به نام‌های «اصل جمع» (Addition Rule) و «اصل ضرب» (Multiplication Rule) می‌پردازیم.

با توجه به مفاهیم منطقی و ذهنی انسان، می‌دانیم اصول قابل اثبات نیستند، ولی همگی (تقریبا همه انسان‌ها) نسبت به صحیح بودن گزاره‌های مربوط به اصول اتفاق نظر دارند. از این روی اثباتی نیز برای اصول شمارش ارائه نمی‌شود و در اینجا درستی این اصول را قبول کرده و فقط به معرفی بعضی از اصول مربوط به شمارش می‌پردازیم.

فیلم اصل شمارش بدون شمردن + روش‌های کاربردی با مثال (فیلم آموزش رایگان) در فرادرس

کلیک کنید

اصل جمع

با توجه به عمل A و B که در بالا اشاره شد، می‌خواهیم به یک عمل جدید مثل Z دست بزنیم که می‌تواند یکی از اعمال A یا B  (و نه هردو) باشد. با توجه به تنوعی که در انجام کارهای A و B‌ داریم، می‌خواهیم حساب کنیم که به چند طریق می‌توانیم کار Z را انجام دهیم. به نظر می‌رسد که همگی نسبت به عدد ۲+۳=۵ اتفاق نظر داریم. بنابراین اگر تعداد حالت‌های انجام عمل A را با |A| و تعداد حالت‌های انجام عمل B را با |B| نشان دهیم، برای تعداد حالت‌های انجام عمل Z‌، طبق اصل جمع داریم:

$$|Z|=|A|+|B|$$

برای مثال اگر برای رفتن از محل کار به خانه (کار Z) بتوان دو روش A (رفتن با دو خط اتوبوس) یا B (رفتن با تاکسی با سه خط مختلف) را انتخاب کرد، مشخص است که طبق اصل جمع، حالت‌های مختلف رسیدن به خانه برابر است با:

$$|Z|=|A|+|B|=2+3=5$$

اصل ضرب

فرض کنید عمل Z، به صورت انجام عمل A و سپس عمل B صورت می‌گیرد. یعنی این کارها باید متوالی و یکی پس از دیگری انجام شوند. اصل ضرب بیان می‌کند که عمل Z می‌تواند به تعداد $$|A|\times |B|$$ صورت مختلف انجام گیرد. زیرا برای هر یک از حالت‌های انجام عمل A، می‌توان به |B| طریق مختلف، عمل B را انجام داد. پس به کمک اصل جمع خواهیم داشت:

$$|Z|=|B|+|B|+|B|+\ldots+|B|$$

که در آن |B|ها به تعداد |A| بار با یکدیگر جمع می‌شوند. پس با استفاده از مفهوم ضرب می‌توان نوشت:

$$|Z|=|A|\times |B|$$

نکته: این دو اصل را می‌توان به k‌ عمل نیز تعمیم داد، در نتیجه می‌توان گفت اگر کار $$A_i$$ را بتوان به $$n_i$$ طریق انجام داد، آنگاه تعداد حالات انجام فقط یکی از کار‌ها طبق اصل جمع به صورت زیر خواهد بود:

$$\sum_{i=1}^k n_i$$

برهمین اساس طبق اصل ضرب، تعداد حالات مختلف برای انجام آن‌ کارها به صورت دنباله‌ای و پیاپی، برابر با رابطه زیر است:

$$\prod_{i=1}^k n_i$$

مثال

فرض کنید برای تشکیل هیئت مدیره یک مجتمع، لازم است که ۲ نفر انتخاب شوند. مجتمع دارای ۳ بلوک است. بلوک A دارای ۵ خانواده، بلوک B دارای ۴ و بلوک C نیز ۶ خانواده ساکن دارد. به چند طریق می‌توان هیت مدیره را تشکیل داد بطوری که اعضای هیئت مدیره همگی از یک بلوک نباشند؟

برای حل این مسئله می‌توان تعداد حالات مربوط به انتخاب هیئت مدیره از هر زوج بلوک را جداگانه محاسبه کرد:

• کار Z1، یعنی انتخاب هیئت مدیره از بلوک A و B: طبق اصل ضرب انتخاب نفر اول به 5 طریق و نفر دوم از هیئت مدیره به ۴ طریق، امکان‌پذیر است. در نتیجه خواهیم داشت: $$|AB|=4\times 5$$
• کار Z2، یعنی انتخاب هیئت مدیره از بلوک B و C: طبق اصل ضرب انتخاب نفر اول به 4 طریق و نفر دوم از هیئت مدیره به 6 طریق، امکان‌پذیر است. در نتیجه خواهیم داشت: $$|BC|=4\times 6$$
• کار Z3، یعنی انتخاب هیئت مدیره از بلوک A و C: طبق اصل ضرب انتخاب نفر اول به 5 طریق و نفر دوم از هیئت مدیره به 6 طریق، امکان‌پذیر است. در نتیجه خواهیم داشت: $$|AC|=5\times 6$$

از آنجایی که فقط یکی از کارهای Z1‌، Z2 یا Z3 صورت خواهد گرفت، طبق اصل جمع، روش‌های ممکن برای انتخاب هیئت مدیره برابر است با:

$$|Z1|+|Z2|+|Z3|=(4\times 5)+(4\times 6)+(5 \times 6)=20+24+30=74$$

همانطور که دیده می‌شود، تعداد حالات برای انجام این کارها، زیاد به نظر می‌رسد و گزینه‌های زیادی برای انتخاب وجود دارد. به این ترتیب، استفاده از اصل ضرب و جمع به ما کمک کردند بدون نوشتن تمامی حالت‌های ممکن برای انتخاب هیئت مدیره، گزینه‌های موجود را بشماریم.

جایگشت و فاکتوریل

فرض کنید می‌خواهید تعداد حالاتی را شمارش کنید که می‌توان یک عدد سه رقمی از ۱، ۲ و ۳ ساخت، بطوری که رقمی تکرار نشود. در این حالت سه کار باید صورت گیرد:

• انتخاب یک رقم برای یکان عدد مورد نظر: تعداد حالت‌ها مختلف برای انجام این کار با توجه به اینکه هر سه رقم امکان دارد در این محل قرار گیرند برابر است با ۳.
• انتخاب یک رقم برای دهگان عدد مورد نظر بطوری که قبلا به کار نرفته باشد: تعداد حالت‌های مختلف برای انجام این کار با توجه به اینکه فقط دو رقم باقی مانده است برابر است با ۲.
• انتخاب یک رقم برای صدگان عدد مورد نظر بطوری که قبلا به کار نرفته باشد: تعداد حالت‌های مختلف برای انجام این کار با توجه به اینکه فقط یک رقم از ارقام ۱ و ۲ و ۳ باقی مانده است برابر است با ۱.

از انجایی که ساختن عدد سه رقمی منوط به انجام کارهای قبلی بصورت دنباله‌ای است، طبق اصل ضرب، تعداد حالت‌هایی که برای ساختن چنین عددی وجود دارد برابر است با $$3\times 2\times 1=6$$

فیلم آموزش آزمون آلس ALES ترکیه – احتمال و هندسه در فرادرس

کلیک کنید

این محاسبه مقدار فاکتوریل ۳ است. به این ترتیب می‌نویسیم:

$$3!=3\times 2\times 1=6$$

این محاسبه نشان می‌دهد که تعداد حالت‌هایی که ارقام 1 , 2, 3 می توانند جابجا شوند (جایگشت داشته باشند)‌ تا یک عدد سه رقمی ایجاد کنند برابر است با ۶.

نکته: اگر در مسئله بالا تکرار مجاز باشد، تعداد حالاتی که می‌توان یک عدد سه رقمی با ارقام ۱ و ۲ و ۳ ساخت ، طبق اصل ضرب برابر است با $$3\times3\times3=3^3=27$$.

با توجه به نحوه قرارگیری اشیاء در کنار یکدیگر باید با دو اصطلاح که در ادامه به کار خواهیم برد آشنا باشیم. منظور از تشکیل صف، قرار گرفتن اشیاء به شکلی است که ترتیب قرارگیری مهم باشد. همانطور که می‌دانید در یک صف، نفر اول، دوم و ... معنی دارد در حالیکه در گروه یا دسته، ترتیب قرارگیری نفرات مهم نیست. پس هرگاه از اصطلاح صف استفاده شود، بیانگر وجود ترتیب در قرارگیری اشیاء است و در صورتی که گروه منظور نظر باشد، ترتیب در تشکیل آن مهم نخواهد بود.

ابتدا به تابع فاکتوریل پرداخته، سپس در مورد قواعد شمارش بیشتر صحبت خواهیم کرد.

فاکتوریل برای اعداد طبیعی

معمولا فاکتوریل را یک تابع در نظر می‌گیرند که دامنه آن مجموعه اعداد طبیعی و برد آن نیز مجموعه اعداد طبیعی است. شیوه محاسبه این تابع برای عدد طبیعی n به صورت زیر تعریف می‌شود:

$$n!=n\times (n-1) \times (n-2)\ldots \times 2\times 1=\prod_{k=1}^n k$$

این رابطه نشان می‌دهد که برای بدست آوردن $$n!$$ باید مقدار n را در همه اعداد طبیعی کوچکتر از خودش ضرب کرد. به این ترتیب مقدار این تابع برای n=5 برابر است با:

$$5!=5\times 4\times 3\times 2 \times 1=120$$

جدول زیر محاسبه فاکتوریل را برای اعداد طبیعی کوچکتر از 15 نشان می‌دهد. (برای محاسبه این مقدارها از تابع Fact اکسل کمک گرفته‌ایم.)

همانطور که قابل مشاهده است، میزان افزایش مقدار فاکتوریل از یک عدد به عدد دیگر رشد زیادی دارد، بطوری که ممکن است برای بیشتر اعداد محاسبه مقدار فاکتوریل حتی توسط کامپیوترها هم میسر نباشد. تصویر زیر  این رشد را در قالب یک نمودار نشان می‌دهد.

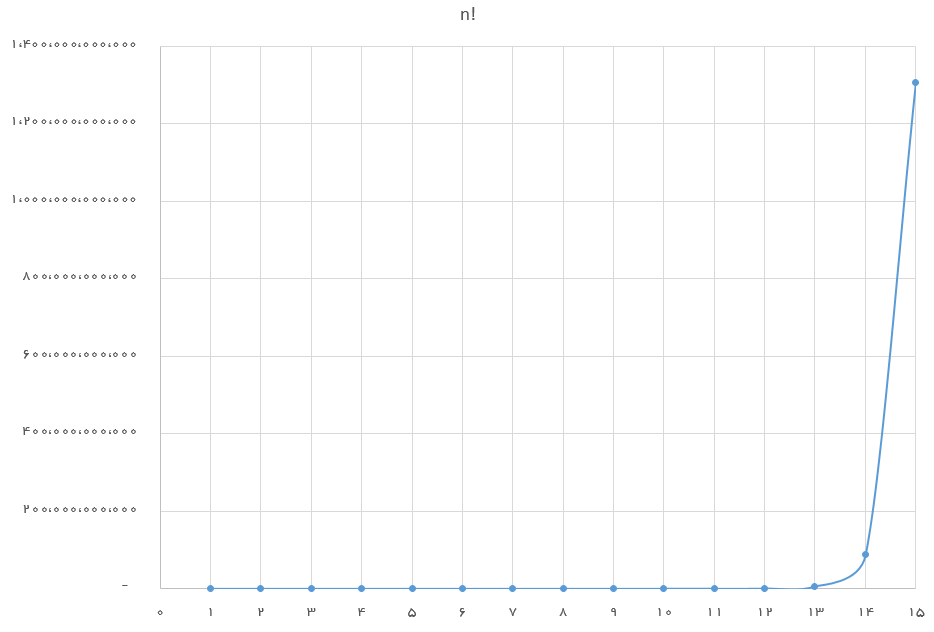
قواعد تابع فاکتوریل

با توجه به مفهومی که برای فاکتوریل مطرح شده، می‌توانیم قواعد زیر را برای محاسبه فاکتوریل در نظر بگیریم.

$$n!=n\times (n-1)!$$

$$n\times (n-1)\times \ldots \times (n-r)=\dfrac{n!}{(n-r-1)!},\;\;\;r$$

در رابطه آخر فرض کنید که r=n-1 باشد. به این ترتیب خواهیم داشت:

$$n\times (n-1)\times \ldots \times (n-(n-1))=\dfrac{n!}{(n-(n-1)-1)!}=\dfrac{n!}{(1-1)!}=\dfrac{n!}{0!}$$

طرف چپ این رابطه، همان !n است. پس به این علت باید فکری به حال !0 بکنیم، تا تساوی برقرار باشد. به همین دلیل طی یک قرارداد در محاسبات مربوط به فاکتوریل، !0=1 در نظر گرفته می‌شود تا محاسبات مربوطه نامفهوم نباشد.

در کل می‌توان رابطه بازگشتی زیر را برای محاسبه $$n!$$ در نظر گرفت

$$1!=1$$

$$n!=n\times(n-1)!$$

اغلب در آموزش برنامه نویسی در زبان‌های مختلف، از دانشجویان خواسته می‌شود برای درک رابطه «بازگشتی» (Recursive)،‌ برنامه‌ای برای محاسبه فاکتوریل اعداد بنویسند. بنابراین کدی که به صورت زیر طراحی شده باشد، برای این کار مناسب به نظر می‌رسد.

همانطور که دیده می‌شود، در این برنامه تابع fact_1 در خود تابع به کار رفته است. این شیوه محاسبه تابع را بازگشتی می‌گویند.

توجه: ممکن است در انجام محاسبات مربوط به فاکتوریل دچار اشتباه شویم. برای جلوگیری از این امر موارد زیر را یادآور می‌شویم:

1. $$(n+m)! \neq n!+m!$$
2. $$(n\times m)!\neq n!\times m!$$
3. $$a(n!)\neq (an)!$$
4. $$(n!)^k\neq (n^k)!$$
5. $$(\frac{n}{m})!\neq\frac{n!}{m!}$$

برای سنجش این نامساوی‌ها، کافی است از مثال‌های عددی کمک بگیرید تا متوجه شوید که این رابطه‌ها با علامت تساوی برقرار نیستند. مثلا برای اینکه نشان دهیم، رابطه ۱ نمی‌تواند بصورت تساوی نوشته شود کافی است $$5!$$ را به صورت زیر بازنویسی کنیم:

$$5!=(2+3)!=120\neq 2!+3!=2+6=8$$

همچنین نامساوی شماره ۵ را می‌توان براساس مثال زیر تایید کرد:

$$4!=(\frac{8}{2})!=24\neq \frac{8!}{2!}=\frac{40320}{2}=20160$$

قواعد ترکیبیاتی و جایگشت

با توجه به مفهوم صف و گروه که در بالا توضیح داده شد و به کمک اصول شمارش می‌خواهیم تعداد حالاتی که می‌توان n شئ متمایز را به صف کرد، بررسی کنیم. فرض کنید برای به صف کردن این اشیاء n جای خالی در نظر گرفته‌ایم. بنابراین تشکیل این صف به n کار تفکیک می‌شود. کار اول (پر کردن خانه اول صف) را می‌توان به n طریق انجام داد.

فیلم آموزش مبانی شمارش در ساختمان گسسته (رایگان) در فرادرس

کلیک کنید

خانه دوم صف نیز با توجه به تمایز اشیاء و قرارگیری یکی از آن‌ها در خانه اول به n-1‌ طریق امکان‌پذیر است. به همین ترتیب برای پر کردن خانه iام (کار در مرحله iام) می‌توان به n-i طریق مختلف اقدام کرد. پس طبق اصل ضرب این کارهای متوالی و پشت سر هم را می‌توان به $$n!$$ طریق انجام داد. پس

تعداد جایگشت‌های n شئ متمایز = $$n!$$

لازم به یادآوری است که تعداد حالات تشکیل گروه برای n شئ متمایز برابر با ۱ است، زیرا قرارگیری آن‌ها در گروه احتیاجی به ترتیب ندارد.

اگر در بین n شئ، تعداد m شئ یکسان (غیرمتمایز) باشند، تعداد حالت‌هایی که می‌توان با آن‌ها یک صف تشکیل داد برابر است با:

$$\dfrac{n!}{m!}$$

نکته: اگر همه این n شئ متمایز نبوده ولی به k گروه متمایز قابل تفکیک باشند، تعداد حالاتی که می‌توان آن‌ها را در یک صف قرار داد به صورت زیر قابل محاسبه است:

$$\dfrac{n!}{n_1!n_2!\ldots n_k!}$$

در اینجا فرض بر این است که $$n_i$$ تعداد اشیاء در گروه iام را نشان می‌دهد. مشخص است که مجموع $$n_i$$ ها برابر با n خواهد بود.

$$\sum_{i=1}^kn_i=n$$

به این ترتیب ابتدا همه اشیاء را متمایز در نظر گرفته‌ایم، سپس تعداد حالات تشکیل صف را شمارش کرده‌ایم (صورت کسر)، در مرحله بعدی تعداد حالاتی که با اشیاء هر گروه می‌توان صف تشکیل داد را شمرده‌ایم که مثلا برای گروه iام برابر با $$n_i!$$ خواهد بود. طبق اصل ضرب، این گروه‌ها می‌توانند به صورت $$n_1!n_2!\ldots n_k!$$ بین خودشان جایگشت داشته باشند. بنابراین نسبت تعداد کل حالت‌ها به جایگشت گروه‌ها، بیانگر تعداد جایگشت‌های مورد نظر ما خواهد بود.

مثال

با استفاده از ازقام ۱،۲،۲،۲،۳،۷،۷ تعداد اعداد ۷ رقمی که می‌توان ساخت برابر است با:

$$\dfrac{n!}{n_1!n_2!\ldots n_k!}=\dfrac{7!}{1!3!1!2!}=\dfrac{5040}{1\times 6\times 2}=420$$

مشخص است که منظور از $$3!$$ تعداد حالاتی است که ۲ ها را می‌توان به صف کرد (۳ همان تعداد تکرارهای رقم ۲ است). همچنین $$2!$$ نیز بیانگر تعداد حالاتی است که می‌توان از ۷ها صف تشکیل داد. از آنجایی که تعداد تکرارهای رقم ۱ و ۳ برابر با یک است، تعداد حالت تشکیل صف با هر یک از آن‌ها برابر با $$1!$$ محاسبه شده است.

ترتیب و ترکیب

از کاربردهای مهم فاکتوریل می‌توان به محاسبه «ترتیب» (Permutation) و «ترکیب» (Combination) اشاره کرد. به کمک این دو شیوه محاسباتی، زمانی که اشیاء درون یک مجموعه زیاد باشند، عمل شمارش حالت‌های مختلف قرارگیری آن‌ها در یک صف (ترتیب) و یا در یک گروه (ترکیب) به راحتی امکان‌پذیر می‌شود. معمولا ترتیب k شئ از n شئ را با $$P_k^n$$ و ترکیب را به صورت $$C_k^n$$ نشان می‌دهند. مشخص است که با توجه به مفهوم صف و گروه، ترتیب قرارگیری اشیاء در ترتیب مهم است ولی در ترکیب، ترتیب قرارگیری مهم نیست. در زیر روابط مربوط به محاسبه هر یک، دیده می‌شود.

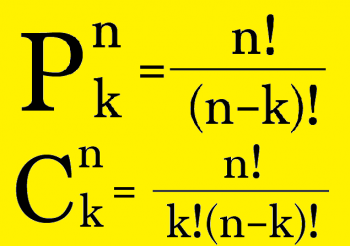
جدول زیر به منظور نمایش شیوه محاسبه تعداد جایگشت‌های n شئ با توجه به وجود تکرار یا عدم تکرار و همچنین انتخاب k شئ از n شئ مجزا را با در نظر گرفتن وجود ترتیب یا عدم ترتیب تنظیم شده است.

به عنوان مثال اگر قرار باشد که از بین ۵ نفر صف‌های ۳ نفری تشکیل دهیم،‌ می‌توان روابط مربوط به جدول بالا را محاسبه کرد.

همانطور که مشخص است، تعداد حالاتی که در آن‌ها تکرار مجاز است، بیشتر از حالاتی است که تکرار مجاز نیست. همچنین با توجه به اینکه در محاسبه ترکیب، بدون توجه به ترتیب قرارگیری اشیاء، آن‌ها را شمارش می‌کنیم، تعداد حالات کمتر از ترتیب است.

البته با توجه به رابطه ترتیب و ترکیب می‌توان تساوی‌های زیر را اثبات کرد.

• $$\left(\begin{array}{c}n\\ 1\end{array}\right) = n$$
• $$\left(\begin{array}{c}n\\ n\end{array}\right) = 1$$
• $$\left(\begin{array}{c}n\\ k\end{array}\right) = \left(\begin{array}{c}n\\ k-1\end{array}\right)$$
• $$\left(\begin{array}{c}n\\ k\end{array}\right) = \left(\begin{array}{c}n-1\\ k-1\end{array}\right)+ \left(\begin{array}{c}n-1 \\ k\end{array}\right)$$

بهتر است در مورد تساوی آخر بیشتر دقت کنیم. این تساوی نشان می‌دهد که انتخاب k شئ از بین n شئ متمایز برابر است با حاصل جمع انتخاب k شئ از n-1 شئ با انتخاب k-1 شئ از n-1 شئ. به نظر می‌رسد، عمل انتخاب می‌تواند براساس دو کار صورت گیرد و طبق اصل جمع، شمارش حالت‌های مختلف محاسبه شود. این توجیه را بواسطه انتخاب k مهره از بین n مهره، توضیح می‌دهیم.

ابتدا از بین n‌ مهره، یکی را خارج می‌کنیم. در نتیجه n-1 مهره باقی خواهد ماند. دو حالت در نظر می‌گیریم یا مهره خارج شده، یکی از k مهره انتخابی ما است یا این چنین نیست. در حالت اول، مشخص است که باید k-1‌ مهره از بین n-1‌ مهره باقی‌مانده، انتخاب شود. در حالت دوم باید k مهره را از بین n-1 مهره باقی‌مانده انتخاب کنیم. پس طبق اصل جمع، نتیجه حاصل خواهد شد.

نکته: گاهی ترتیب k شئ از n شئ را به صورت $$(n)_k$$ نیز نشان می‌دهند. همینطور ترکیب k شئ از n شئ نیز به صورت $${n \choose k}$$ قابل نمایش است.

فاکتوریل دوبل (Double Factorial)

فاکتوریل دوبل، یک عملگر ریاضی است که محاسبه آن شبیه محاسبه فاکتوریل عادی است با این تفاوت که برای اعداد فرد و زوج جداگانه محاسبه می‌شود. فاکتوریل دوبل عدد n را با $$n!!$$ نشان می‌دهند.

فرض کنید n عددی زوج باشد، منظور از $$n!!$$‌ حاصلضرب n در همه اعداد زوج کمتر از خودش است. به این ترتیب می‌توان نوشت:

$$\large n!! =\prod_{k=1}^{\frac{n}{2}}(2k)=n(n-2)(n-4)\cdots 4\times 2$$

برای مثال فاکتوریل دوبل ۶ برابر است با:

$$\large 6!! =6\times 4\times 2 = 48$$

به همین ترتیب اگر n عددی صحیحی و فرد باشد، فاکتوریل دوبل آن مطابق رابطه زیر قابل محاسبه است.

$$\large n!! =\prod_{k=1}^{\frac{n+1}{2}}(2k-1)=n(n-2)(n-4)\cdots \times 3\times 1$$

برای مثال فاکتوریل دوبل ۷ برابر است با:

$$\large 7!! =7\times 5\times 3 \times 1 = 105$$

این تعریف در حوزه‌های مختلف کاربرد داشته و برای مثال برای محاسبه مشتق مراتب بالاتر چندجمله‌ای‌ها به کار می‌رود.

تابع گاما و محاسبه فاکتوریل برای اعدادی حقیقی

همانطور که به یاد دارید، فاکتوریل به عنوان تابعی با دامنه و برد اعداد حقیقی شناخته شد. به کمک تابع گاما می‌توان مفهوم فاکتوریل را به اعداد حقیقی نامنفی نیز گسترش داد. دامنه این تابع، اعداد حقیقی (بدون اعداد صحیح منفی) و برد آن همه اعداد حقیقی است. تابع گاما به صورت زیر تعریف می‌شود.

$$\large \displaystyle \Gamma (z)=\int _{0}^{\infty }x^{z-1}e^{-x}\;dx$$

نمودار این تابع برای فاصله 5- تا ۵ در تصویر زیر دیده می‌شود. مشخص است که این تابع برای مقدارهای صحیح منفی قابل محاسبه نیست و برای مقدارهای صحیح مثبت مثل n نیز برابر با فاکتوریل n-1 خواهد بود. یعنی اگر n عدد صحیح مثبتی باشد، خواهیم داشت: $$\Gamma(n)=(n-1)!$$.

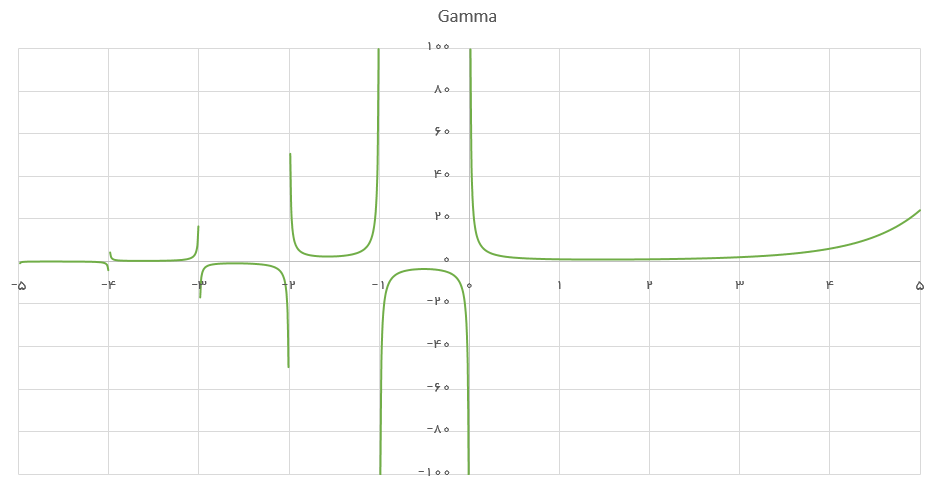
از خصوصیات جالب برای تابع گاما می‌توان به رابطه‌های زیر اشاره کرد:

• $$\Gamma(z+1)=z\Gamma(z)$$
• $$\Gamma(1)=1$$
• $$\Gamma(n)=(n-1)!$$
• $$\Gamma(\frac{1}{2})=\sqrt{\pi}$$

همانطور که دیده می‌شود، این خصوصیات در زمانی که 1+z، عددی از مجموعه اعداد طبیعی باشد، با خصوصیات فاکتوریل z یکسان است. همچنین آخرین تساوی نشان می‌دهد که می‌توان برای محاسبه تقریبی عدد $$\pi$$‌ نیز از انتگرال مربوط به تابع گاما استفاده کرد.