معادلات دیفرانسیل — به زبان ساده

در این مطلب در مورد یکی از مهم‌ترین مفاهیم تاریخ علم، یعنی «معادلات دیفرانسیل» (differential equation)، صحبت شده است. معادله دیفرانسیل، رابطه‌ای میان تابع، مشتقات آن و متغیرهای مستقل‌اش است. بنابراین ما خواهیم توانست، انواع محاسبات را انجام دهیم، از هر پدیده‌ای نموداری به منظور توصیف آن تهیه کنیم و حتی قادر خواهیم بود آینده را پیش بینی کنیم!

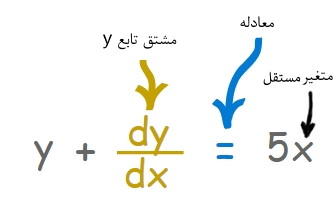
نمونه‌ای از یک معادله دیفرانسیل که شامل تابع y و مشتقش است.

اگر می‌خواهید خیلی سریع، راحت و اصولی، مفاهیم مرتبط با معادلات دیفرانسیل، نرم‌افزارهای مدل‌سازی معادلات دیفرانسیل و حتی کاربرد این نوع معادلات در مسائل واقعی را یاد بگیرید، فیلم‌های مجموعه آموزش معادلات دیفرانسیل – درس، تمرین، حل مثال و تست در فرادرس را مشاهده کنید.

حل شدن یک معادله دیفرانسیل به چه معناست؟

زمانی یک معادله دیفرانسیل حل شده است که تابع y بر حسب متغیر‌های وابسته‎‌اش پیدا شده باشد. به طور دقیق‌تر، یعنی اینکه بدانیم مثلا y که تابعی از متغیر x در نظر گرفته‌شده، طبق کدام رابطه توصیف می‌شود. روش‌های متفاوتی به منظور حل یک معادله دیفرانسیل وجود دارند، اما در ابتدا بایستی بدانیم که چرا معادلات دیفرانسیل مهم هستند.

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

برای آشنایی با نمونه سوالات معادلات دیفرانسیل، به مطلب «نمونه سوال معادلات دیفرانسیل + جواب و راه حل» مراجعه کنید.

چرا معادلات دیفرانسیل مفید هستند؟

در دنیایی زندگی می‌کنیم که پدیده‌ها دائماً در حال تغییر هستند. این در حالی است که می‌توان اکثر این دگرگونی‌ها را با استفاده از معادلات دیفرانسیل توصیف کرد. به عنوان مثال، آلبرت انیشتین به منظور توصیف نیروی گرانشی از معادلات دیفرانسیل استفاده کرد؛ او به کمک این معادلات هم این نیرو را توضیح داد و هم ثابت کرد که امکان سفر به آینده امکان‌پذیر است! در ادامه، دو مثال کاربردی از این معادلات ارائه می‌دهیم.

یکی از مهم‌ترین معادلات تاریخ علم فیزیک، معادله «ناویر-استوکس» (Navier-stokes) است که کاربرد بسیاری در طراحی اجسام پرنده دارد.

مثال ۱: رابطه بین جمعیت خرگوش‌ها و معادله دیفرانسیل

هرچه خرگوش بیشتری وجود داشته باشد، بچه خرگوش بیشتری نیز وجود خواهد داشت. این بچه‌ خرگوش‌ها نیز بزرگ خواهند شد و تولید مثل خواهند کرد. بنابراین با گذشت زمان تعداد خرگوش‌ها بیشتر و بیشتر خواهند شد. خب اجازه دهید ببینیم این روند زیاد شدن به چه شکل و با چه سرعتی اتفاق می‌افتد. به این منظور در ابتدا فرضیات زیر را در نظر می‌گیریم.

• N: تعداد خرگوش‌ها در زمان t
• r: نرخ تولد (منظور از نرخ تولد، تعداد خرگوش‌هایی است که یک خرگوش و در یک بازه‌ زمانی معین تولید می‌کند.)
• dN/dt: سرعت زیاد شدن تعداد کل خرگوش‌ها

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

حال این اعداد را در قالب یک مثال واقعی فرض کنید:

• در حال حاضر تعداد کل خرگوش‌ها برابر با N=1000 است.
• هر خرگوش در یک هفته r=0.01 بچه تولید می‌کند.

با دو فرض در نظر گرفته شده در بالا، می‌توان نتیجه گرفت که کل خرگوش‌ها در هر هفته، تعداد dN/dt=1000×0.01=10 بچه جدید به وجود می‌آورند. توجه کنید که این اعداد فقط با یک مقطع زمانی معین ارتباط دارند و به این معنی نیستند که خرگوش‌ها دائماً در حال افزایش هستند. بنابراین، بهتر است بگوییم که نرخ زیاد شدن تعداد خرگوش‌ها در هر لحظه برابر است با: dN/dt=rN. اگر خوب دقت کنید، این رابطه یک معادله دیفرانسل محسوب می‌شود چرا که در آن (N(t به صورت تابعی از مشتقاتش بیان شده است.

این جا است که به قدرت ریاضیات پی می‌بریم. این معادله می‌گوید: «نرخ رشد جمعیت خرگوش‌ها بر واحد زمان برابر با حاصل ضرب نرخ رشد در تعداد آن‌ها است.»

معادلات دیفرانسیل به ما می‌گویند که چگونه جمعیت زیاد می‌شود، حرکت گرما به چه شکل است، فنر طبق کدام الگو نوسان می‌کند و به همین ترتیب تجزیه شدن مواد رادیواکتیو و بسیاری دیگر از پدیده‌ها را توصیف می‌کنند. لازم به ذکر است که این معادلات، طبیعی‌ترین راه به منظور نشان دادن مکانیزم کارکرد کائنات هستند. در ادامه به بررسی مثالی کاربردی می‌پردازیم که ممکن است روزی به کمک‌تان بیاید.

مثال ۲: بهره مرکب

اندوخته پولی، منجر به ایجاد بهره خواهد شد؛ بهره این اندوخته را می‌توان سالانه، ماهانه و به شیوه‌های دیگر محاسبه کرد. نهایتا بهره محاسبه شده به مقدار اولیه اضافه خواهد شد. این مفهوم، بهره مرکب نامیده می‌شود.

زمانی که بهره به صورت دائمی وجود داشته باشد، میزان اندوخته انباشه شده در زمان نیز، پیوسته افزایش می‌یابد. این در حالی است که هرچه اندوخته بیشتر باشد، بهره به دست آمده نیز بیشتر خواهد بود. به منظور درک بهتر به مثال ارائه شده در ادامه توجه فرمایید. در این مثال از نماد‌های زیر استفاده می‌کنیم:

• t: زمان
• r: نرخ بهره
• V: مقدار سرمایه اندوخته شده

با توجه به فرض صورت گرفته، می‌توان میزان سرمایه ذخیره شده در واحد زمان را با استفاده از رابطه زیر توصیف کرد:

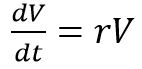
نکته جالب اینکه رابطه مورد اشاره بسیار شبیه به تفسیر معادلات دیفرانسیل در مورد زیاد شدن خرگوش‌ها است و فقط نماد‌ها هستند که تغییر کرده‌اند. بنابراین ریاضیات به ما نشان می‌دهد که چگونه دو پدیده می‌توانند مشابه یکدیگر رفتار کنند.

حل یک معادله دیفرانسیل

معادلات دیفرانسیل همواره در توضیح پدیده‌ها به ما کمک می‌کنند، اما استفاده از آن‌ها نیز معمولا مشکل به نظر می‌رسد. خوشبختانه معادله بیان شده در مثال قبلی - با استفاده از روش جداسازی متغیر‌ها - قابل حل است. پاسخ معادله نرخ بهره عبارت است از:

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

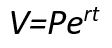
در این رابطه P مقدار سرمایه اولیه است. به عنوان مثال اگر ما ابتدا 1000 تومان در بانک ذخیره داشته باشیم و مقدار بهره آن %10 باشد، بعد از گذشت 2 سال، سرمایه ما به مقدار زیر خواهد بود.

بنابراین معادلات دیفرانسیل بسیار مفید و کاربردی خواهند بود، به شرط آنکه راه صحیح حل کردن آن‌ها را پیدا کنیم. برای آشنایی بهتر با معادلات دیفرانسیل و چگونگی حل انواع این معادلات می‌توانید به مجموعه آموزش ریاضیات دانشگاهی فرادرس مراجعه کنید.

بررسی بیشتر معادلات دیفرانسیل

در این قسمت به بررسی بیشتر مثال‌ ارائه شده در مورد تعداد خرگوش‌ها می‌پردازیم؛ هم‌چنین مثالی از کاربرد معادله دیفرانسیل در تحلیل حرکت نوسانی جرم و فنر ارائه خواهیم داد.

معادله ورهولست

همان‌طور که در بخش‌های قبل بیان شد، سرعت زیاد شدن خرگوش‌ها را می‌توان با استفاده از معادله زیر توصیف کرد.

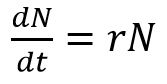
دقت شود که در واقعیت این رابطه برقرار نخواهد بود چرا که ممکن است همیشه برای تعداد N خرگوش، منبع تغذیه موجود نباشد. به منظور بهتر کردن این معادله، فرض می‌کنیم:

• K: بیشترین جمعیت خرگوش‌ها است که منبع غذایی برای آن‌ها وجود دارد.

با توجه به فرض در نظر گرفته شده، ریاضی‌دانی به نام «فردیناند ورهولست» (Ferdinand Verhulst)، این معادله را به شکل زیر بیان کرد:

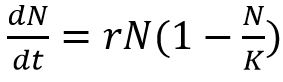
علت اضافه شدن عبارت N/K این است که نشان دهیم تا زمانی این رابطه برقرار است که جمعیت خرگوش‌ها به عدد k نرسیده باشد.

حرکت نوسانی ساده

در فیزیک، مبحثی به نام «حرکت دوره‌ای» (Periodic Motion) وجود دارد. ساده‌ترین نوع این حرکت، «حرکت نوسانی ساده» (Simple Harmonic Motion) است. به منظور تحلیل و بررسی سیستم جرم و فنر، آن را به صورت نوسانی ساده در نظر می‌گیرند. در چنین سیستمی نیروی ذخیره شده در فنر با افزایش طول آن زیاد می‌شود.

در ابتدا فنری را در نظر بگیرید که جرمی به آن متصل شده‌ است. با توجه به این فرض، نوسان جرم طی مراحل زیر اتفاق خواهد افتاد:

• این جرم به دلیل نیروی گرانشی به سمت پایین کشیده می‌شود.
• به دلیل زیاد شدن طول فنر، نیروی کششی در آن افزایش می‌یابد.
• به تدریج سرعت جرم، کم خواهد شد.
• نیروی کششی موجود در فنر، جرم را به سمت بالا می‌کشد.
• دوباره جرم به سمت پایین حرکت خواهد کرد و مرتبا این مراحل تکرار خواهند شد.

حال می‌خواهیم موارد بیان شده را در قالب ریاضیات بیان کنیم. در ابتدا جرم به سمت پایین کشیده می‌شود. هم‌چنین از قانون دوم نیوتن می‌دانیم که نیرو، برابر با حاصل ضرب شتاب در جرم است. بنابراین خواهیم داشت:

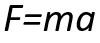
و یا به صورت دقیق‌تر می‌توان گفت که شتاب همان مشتق دوم جابه‌جایی نسبت به زمان است. در نتیجه:

در مرحله‌ بعد، فنر جرم را با استفاده از نیروی ذخیره شده در خود، به سمت بالا می‌کشد. برای هر فنر می‌توان پارامتری به نام k تعریف کرد که آن را «سختی فنر» (Spring Stiffness) می‌نامند. نیروی ذخیره شده در فنری که به اندازه x کِش آمده، برابر است با:

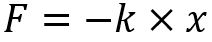
با فرض ناچیز بودن نیروی گرانش در مقابل نیروی کشش فنر، دو عبارت بیان شده در بالا همواره با هم برابر خواهند بود. در نتیجه می‌توان نوشت:

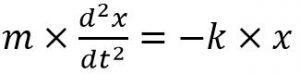
همان‌طور که در این معادله می‌بینید، تابع (x(t بر حسب مشتق دومش و نیز خودِ (x(t بیان شده است. بنابراین ما با یک معادله دیفرانسیل روبرو هستیم. توجه شود که در این معادله از نیروی اصطکاک صرف‌نظر شده است. با فرض وجود داشتن اصطکاک، عبارتی جدید به معادله بالا اضافه خواهد شد که آن را پیچیده‌تر می‌کند.

تولید صدا که در نتیجه ارتعاش بخش‌های مختلف وسایل حمل و نقل عمومی است با استفاده از مفهوم ساده جرم و فنر و به کارگیری معادلات دیفرانسل قابل توصیف است.

دسته‌بندی معادلات دیفرانسیل

چگونه یک معادله دیفرانسیل حل می‌شود؟ بدیهی است که همیشه پاسخ به این سوال آسان نخواهد بود. از سال‌های دور تاکنون افراد زیادی به دنبال راه‌حل‌های جدیدی به منظور حل این معادلات بوده‌اند. بنابراین به منظور تسلط بر موضوع بایستی با نوع یک معادله آشنا باشیم.

تصور کنید که می‌خواهید به مسافرت بروید. احتمالا با روش‌های مختلفی می‌توانید این کار را انجام دهید. مثلا سفر با هواپیما، خودرو شخصی و یا حتی ممکن است با پای خود قصد سفر کنید. البته اگر هدف شما سفر به کهکشان دیگری باشد احتمالا بایستی چند صد سال منتظر بمانید تا ابزار مناسب این سفر اختراع شود!

حل کردن معادلات دیفرانسیل نیز همانند سفر رفتن است و احتمال دارد با چند روش بتوانید یک معادله دیفرانسیل را حل کنید. بنابراین قصد داریم در این قسمت انواع مختلف معادلات دیفرانسیل را معرفی کنیم.

ساده یا پاره‌ای

قبل از حل معادلات دیفرانسیل مهم‌ترین کار این است که بدانیم این معادله ساده یا با مشتقات جزئی است.

فیلم آموزش معادلات دیفرانسیل با میپل Maple در فرادرس

کلیک کنید

• معادلات دیفرانسیل ساده (ODE)، به معادلاتی گفته می‌شود که در آن یک متغیر مستقل وجود داشته باشد.
• معادلات دیفرانسیل با مشتقات پاره‌ای (PDE)، معادلاتی هستند که در آن‌ها دو یا چند متغیر مستقل وجود داشته باشد.

به عنوان مثال، در معادله جرم و فنر، تابع (x(t فقط به متغیر زمان (t) وابسته است. بنابراین این معادله یک معادله ساده محسوب می‌شود. اما معادله دیفرانسیلی را فرض کنید که در آن تابع p به متغیر‌های x,y,z,t وابسته است. یعنی:

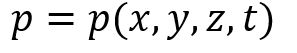
همان‌طور که در معادله زیر می‌بینید، p تابعی از 4 متغیر مستقل است. بنابراین معادله دیفرانسیل زیر نمونه‌ای از PDE خواهد بود.

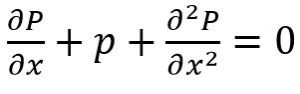
در معادلات PDE، مشتقات را با علامت ∂ و در ODE، با d نشان می‌دهند.

مرتبه و درجه یک معادله دیفرانسیل

در ادامه به دو مشخصه مهم یک معادله دیفرانسیل، یعنی «مرتبه» (Order) و «درجه» (Degree) خواهیم پرداخت.

مرتبه

مرتبه، بالاترین مشتق گرفته‌شده از تابع وابسته، در یک معادله است. به عنوان مثال معادله زیر از مرتبه اول است چراکه بزرگ‌ترین مشتق موجود در آن، مشتق اول تابع y نسبت به متغیر dy/dx) x) است.

به منظور توضیح دقیق‌تر، معادله زیر را در نظر بگیرید:

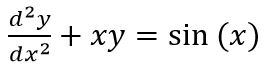
به دلیل وجود عبارت d2y/dx2 این معادله از مرتبه دوم است. به نظر شما معادله زیر از مرتبه چندم است؟

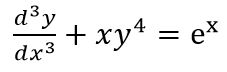
بله شما درست حدس زدید؛ این معادله از مرتبه سوم است.

درجه

درجه معادله دیفرانسیل، توان بزرگ‌ترین مشتق موجود در آن محسوب می‌شود. معادله زیر را در نظر بگیرید:

به نظر شما مرتبه و درجه این معادله چند هستند؟ به منظور پاسخ صحیح، ابتدا به بزرگ‌ترین مشتق موجود در معادله نگاه می‌کنیم. همان‌طور که در معادله می‌بینید، بزرگترین مشتق آن (dy/dx) از مرتبه 1 است. حال به سراغ توان آن می‌رویم؛ همان‌طور که می‌بینید توان این عبارت، 2 است؛ بنابراین درجه این معادله نیز 2 است. حال وقت آن است که مثال مشکل‌تری را بررسی کنیم. معادله زیر را در نظر بگیرید:

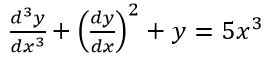
بزرگ‌ترین مشتق موجود در این معادله از مرتبه 3 و توان آن 1 است. بنابراین این یک معادله ODE از مرتبه 3 و درجه 1 محسوب می‌شود. توجه کنید که درجه و مرتبه یک معادله دیفرانسیل با یکدیگر متفاوت هستند.

خطی بودن یک معادله

به معادله دیفرانسیلی خطی گفته می‌شود که تمام توابع و مشتقات موجود در آن خطی باشند. عباراتی که در زیر آمده‌اند، معادله را غیر خطی می‌کنند.

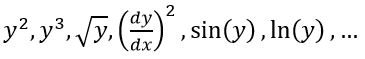
دقت شود که تنها، غیر خطی بودن تابع وابسته و مشتقاتش منجر به غیر خطی شدن معادله می‌شوند. به عنوان مثال عباراتی که در زیر آمده‌اند، معادله را غیر خطی نمی‌کنند.

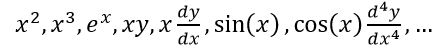
در آینده در مورد حل انواع معادلات دیفرانسیل به صورت مفصل بحث خواهیم کرد.