قضیه بیز (Bayes Theorem) در احتمال شرطی و کاربردهای آن (+دانلود فیلم آموزش رایگان)

در این آموزش قصد داریم تا در خصوص قضیه بیز (Bayes theorem) در احتمال شرطی صحبت و برای آن، مثال‌هایی ذکر کنیم.

قضیه بیز (Bayes Theorem) در احتمال شرطی

زمانی که از قبل وقوع یک پیشامد تصادفی را بدانیم، به کمک فرمول‌های احتمال شرطی می‌توانیم مقدار احتمال برای هر پیشامد دیگر را محاسبه کنیم.

فیلم آموزش نظریه صف Queueing theory در فرادرس

کلیک کنید

طبق فرمول احتمال شرطی با در نظر گرفتن اینکه $$P(B)>0$$ (یعنی پیشامد B یک پیشامد محال نباشد)، داریم:

$$P(A|B)=\dfrac{P(A \cap B)}{P(B)}$$

حال اگر فضای نمونه براساس رخداد یا عدم رخداد پیشامد B تفکیک شود، برای بدست آوردن احتمال A ‌می‌توانیم دو حالت در نظر بگیریم: یا پیشامد B رخداده، یا رخ نداده است. با این کار فضای نمونه را به B و ‌$$B\prime$$ افراز کرده‌ایم (منظور از $$B\prime$$ مکمل پیشامد B‌ است).

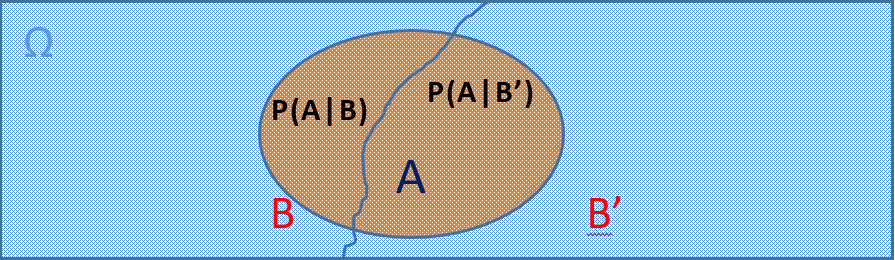
محاسبه احتمال براساس افراز

منظور از افراز یک پیشامد مثل B، ایجاد زیرمجموعه‌های مثل $$B_1$$، $$B_2$$ و ... $$B_n$$ است بطوری که این پیشامدها دو به دو ناسازگار باشند و اجتماع آن‌ها مجموعه B را بسازد. این موضوع را به زبان ریاضی به صورت زیر می‌نویسیم:

$$B_i\cap B_j=\emptyset, \;\;\; i\neq j$$

$$B=\cup_{i=1}^n B_i$$

و در این حالت می‌گوییم، $$B_i$$ها یک افراز روی B ایجاد می‌کنند.

با توجه به این تعریف فرض کنید که B و ‌$$B\prime$$ یک افراز روی $$\Omega$$ باشند. در این صورت احتمال پیشامد A را می‌توانیم به صورت زیر بنویسیم:

$$P(A)=P(A\cap \Omega)=P(A \cap (B\cup B\prime)=P(A\cap B)+P(A\cap B\prime)$$

با توجه به قانون ضرب احتمال خواهیم داشت:

$$P(A)=P(A|B)P(B)+P(A|B\prime)P(B\prime)$$

و در حالت کلی‌تر اگر افراز را ظریف‌تر کنیم،‌ به صورتی که $$B_1, B_2, \ldots,B_n$$ یک افراز روی $$\Omega$$ باشند، آنگاه احتمال پیشامد A به صورت زیر محاسبه می‌شود:

$$P(A)=\sum_{i=1}^nP(A|B_i)P(B_i)$$

مثال ۱

سه سبد در اختیار داریم که در سبد اول دو مهره سفید و یک مهره قرمز و در سبد دوم یک مهره سفید و یک مهره قرمز و در سبد سوم نیز دو مهره سفید و سه مهره قرمز قرار دارد. از این سبدها یک مهره خارج می‌کنیم. احتمال اینکه مهره سفید خارج شود چقدر است؟

فرض کنید فضای نمونه را به $$B_1,B_2,B_3$$‌ افراز کرده باشیم، به این معنی که یکی از سبدها انتخاب شده باشد. همچنین اگر پیشامد A را مشاهده مهره سفید در نظر بگیریم، اطلاعات زیر در اختیارمان قرار دارد:

$$P(B_1)=P(B_2)=P(B_3)=\dfrac{1}{3}$$

زیرا احتمال اینکه هر یک از سبدها انتخاب شود با دیگری برابر است.

$$P(A|B_1)=\dfrac{2}{3},\;\;P(A|B_2)=\dfrac{1}{2},\;\;P(A|B_3)=\dfrac{2}{5}$$

حال برای پاسخ، محاسبات زیر را براساس قانون ضرب احتمال انجام می‌دهیم.

$$P(A)=P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+P(A|B_3)P(B_3)$$

$$(\dfrac{2}{3})(\dfrac{1}{3})+(\dfrac{1}{2})(\dfrac{1}{3})+(\dfrac{2}{5})(\dfrac{1}{3})=\dfrac{47}{90}$$

اکنون بر مبنای قضیه بیز می‌خواهیم برعکس عمل کنیم و احتمال هر یک از افرازها را براساس اینکه بدانیم پیشامد A رخداده است محاسبه کنیم.

قضیه بیز (Bayesian Theorem)

اگر فضای نمونه $$\Omega$$ توسط $$B_1, B_2, \ldots,B_n$$ افراز شده باشد، بطوری که $$P(B_i)>0$$ آنگاه برای هر پیشامد A می‌توانیم بنویسیم:

$$P(B_j|A)=\dfrac{P(B_j)P(A|B_j)}{P(A)}$$

زیرا براساس رابطه احتمال شرطی می‌دانیم:

$$P(B_j|A)=\dfrac{P(B_j\cap A)}{P(A)}=\dfrac{P(A|B_j)P(B_j)}{P(A)}$$

که تساوی آخر براساس قانون ضرب احتمال نوشته شده است.

فیلم آموزش ریاضی برای یادگیری ماشین + پیاده سازی در پایتون در فرادرس

کلیک کنید

این قانون را برای دو پیشامد A و B یادآوری می‌کنیم: $$P(B\cap A)=P(A|B)P(B)$$.

گاهی رابطه مربوط به قضیه بیز را به صورت زیر که معادل قضیه اصلی است، می‌نویسند:

$$P(B_j|A)=\dfrac{P(B_j)P(A|B_j)}{\sum_{i=1}^nP(B_i)P(A|B_i)}$$

نام این قضیه به افتخار دانشمند انگلیسی آمار «توماس بیز» (Thomas Bayes) که در سال‌ 1763 مقاله‌ای با این موضوع منتشر کرد، انتخاب شده است.

مثال ۲

در مثال ۱، اگر بدانیم مهره‌ای که از سبد خارج شده، سفید است، احتمال اینکه این مهره از سبد سوم خارج شده باشد چقدر است؟

بر طبق قضیه بیز باید احتمال زیر را محاسبه کنیم:

$$P(B_3|A)=\dfrac{P(A|B_3)P(B_3)}{P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+P(A|B_3)P(B_3)}=\dfrac{12}{47}$$

احتمال پیشین و پسین در قضیه بیز

زمانی که بدون اطلاع از پیشامدهای دیگر در مورد رخداد یک پیشامد خاص احتمال را محاسبه می‌کنیم، احتمال پیشین را بدست آورده‌ایم. ولی زمانی که از احتمال رخداد یک پیشامد دیگر از قبل مطلع هستیم در مورد رخداد یک پیشامد خاص قضاوت بهتری خواهیم داشت و از اطلاعات قبلی برای محاسبه احتمال آن پیشامد استفاده می‌کنیم. در این حالت به محاسبه احتمال پسین پرداخته‌ایم.

مثال ۳

در یک آزمایش پزشکی، دیابت (مرض قند) یک فرد قندی با احتمال 0.8 به درستی تشخیص داده می‌شود و با احتمال 0.9 نیز برای افراد سالم نتیجه عدم ابتلا به این بیماری اعلام می‌شود. اگر از هر ۱۰.۰۰۰ نفر مردم جامعه ۲ نفر دچار بیماری دیابت باشند (احتمال پیشین)، احتمال اینکه نتیجه مثبت آزمایش یک فرد، بیانگر ابتلا به مرض قند باشد چقدر است (احتمال پسین)؟

با توجه به مسئله، جامعه آماری یا فضای نمونه به دو گروه بیماران قندی و سالم طبقه‌بندی (افراز) شده است. حال اگر B را پیشامد ابتلا به دیابت و $$B\prime$$ را عدم ابتلا به بیماری دیابت در نظر بگیریم و A پیشامد این باشد که نتیجه آزمایش مثبت است، اطلاعات زیر توسط مسئله داده شده.

A|B: پیشامد اینکه نتیجه آزمایش مثبت برای فرد مبتلا به دیابت باشد. یعنی آزمایش نشان دهد که فرد دیابتی مبتلا به بیماری دیابت است.

$$A\prime |B\prime$$: پیشامد اینکه نتیجه آزمایش منفی مربوط به فرد سالم باشد. یعنی آزمایش نشان دهد که فرد سالم به دیابت دچار نیست. در نتیجه خواهیم داشت:

 $$P(A|B)=0.8,\;\;\;P(A\prime |B\prime)=0.9, \;\;\; P(B)=0.0002$$

حال با استفاده از قضیه بیز می‌توانیم بنویسیم:

$$P(B|A)=\dfrac{P(A|B)P(B)}{P(A|B)P(B)+P(A|B\prime)P(B\prime)}=$$

$$\dfrac{0.8\times 0.0002}{0.8\times 0.0002+(1-0.9)\times (1-0.0002)}=0.0016$$

به این ترتیب طبق قضیه بیز، آگاهی از مثبت بودن نتیجه آزمایش احتمال مبتلا بودن فرد به بیماری دیابت را به میزان 0.0014 افزایش داد (احتمال پسین). درحالیکه احتمال ابتلا به بیماری قند برای او در حالتی که آزمایش پزشکی انجام نشده بود برابر با 0.0002 بود.

با محاسبات مشابه می‌توان جدول زیر را تکمیل کرد.

نکته: براساس یک تعریف غیر رسمی، احتمال پیشامد $$A$$ برابر با تعداد حالت‌های مطلوب آن پیشامد (تعداد اعضای مجموعه $$A$$) به کل حالت‌ها (تعداد اعضای مجموعه فضای نمونه $$\Omega$$) می‌باشد. در زمانی که احتمال شرطی $$P(A|B)$$ محاسبه می‌شود، تعداد حالت‌های مطلوب براساس تعداد اعضای مشترک بین پیشامد $$A$$ و $$B$$ ملاک قرار گرفته و تعداد کل حالت‌ها نیز به اندازه مجموعه $$B$$ کاهش پیدا می‌کند. یعنی در اینجا فضای نمونه تبدیل به پیشامد $$B$$ می‌شود. از آنجایی که تابع احتمال شرطی باید در اصول و قضیه‌های تابع احتمال صدق کند، رابطه زیر برقرار است.

$$\large P(A\prime|B)+P(A|B)=\dfrac{P(A\prime \cap B)}{P(B)}+\dfrac{P(A\cap B)}{P(B)}= \dfrac{P([(A\prime \cup A)\cap B]}{P(B)}=\dfrac{P(\Omega\cap B)}{P(B)}=1$$

به این ترتیب مشخص است که $$P(A\prime |B)=1-P(A|B)$$.

اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزش‌هایی که در ادامه آمده‌اند نیز برایتان کاربردی خواهند بود.

• متغیر های تصادفی – میانگین، واریانس و انحراف معیار – به زبان ساده
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• احتمال شرطی (Conditional Probability) --- اصول و شیوه محاسبه
• آموزش آمار و احتمال مهندسی
• آزمایش تصادفی، پیشامد و تابع احتمال