رگرسیون لجستیک (Logistic Regression) — مفاهیم، کاربردها و محاسبات در SPSS

اغلب برای بیان شدت رابطه خطی بین دو متغیر کمی از ضریب همبستگی استفاده میکنیم. همچنین برای نمایش مدل رابطه بین آن دو نیز از مدل رگرسیونی کمک میگیریم. در این میان یک الگو برای پیشبینی متغیر وابسته (Y) براساس متغیر مستقل (X) ایجاد میشود. ولی باید توجه داشت که در مدل ایجاد شده، هر دو متغیر مستقل و وابسته، کمی هستند. همچنین شرط پیوسته بودن این مقدارها نیز در روش رگرسیون نهفته است. ولی ممکن است بخواهیم رابطه بین یک متغیر مستقل (با مقدارهای پیوسته) را با یک متغیر وابسته با مقدارهای کیفی بسنجیم. در این حالت روش عادی رگرسیون خطی جوابگو نخواهد بود و باید از «رگرسیون لجستیک» (Logistic Regression) استفاده کرد.
از رگرسیون لجستیک برای تحلیل رابطه بین متغیرها بخصوص در زمینههای پزشکی، روانشناسی و علوم اجتماعی بسیار کمک گرفته میشود. برای مثال بررسی و ایجاد مدل رابطه بین میزان فعالیت روزانه و ابتلا به بیماری قند یک نمونه از تحلیلهایی است که در آن از مدل رگرسیون لجستیک کمک میگیرند. در این حالت متغیر مستقل، فعالیت روزانه با مقدارهای کمی است و متغیر وابسته کیفی نیز ابتلا یا عدم ابتلا به بیماری قند است که دارای دو مقدار ۰ و یا ۱ خواهد بود. همچنین در تحلیل حافظه انسان و رابطه آن با میزان خواب، روانشناسان آزمایشی را انجام میدهند که براساس مقدار ساعات متفاوت خواب افراد، یادآوری یا فراموشی کلمهای را میسنجند. در این حالت میزان خواب متغیر مستقل با مقدارهای کمی پیوسته و متغیر وابسته کیفی با دو مقدار ۰ به معنی فراموشی و ۱ به معنی یادآوری صحیح است.
از آنجایی که در استفاده از رگرسیون لجستیک مفاهیم اولیه رگرسیون به کار میروند، پیشنهاد میشود ابتدا مطلب مربوط به رگرسیون خطی — مفهوم و محاسبات به زبان ساده را خوانده، سپس به مطالعه این قسمت بپردازید.
رگرسیون لجستیک (Logistic Regression)
یکی از روشهای «دستهبندی» (Classification) در مبحث «آموزش نظارت شده» (Supervised Machine Learning) رگرسیون لجستیک است. در این روش رگرسیونی، از مفهوم و شیوه محاسبه «نسبت بخت» (Odds Ratio) استفاده میشود. بنابراین بهتر است ابتدا با این مفهوم آشنا شویم.
بخت (Odd)
برای آشنایی با مفهوم بخت به یک مثال میپردازیم. فرض کنید در یک خانواده که دارای شش فرزند هستند، نسبت پسرها به دخترها برابر است با . این نسبت نشان میدهد که تعداد دخترها در این خانواده دو برابر تعداد پسرها است. از طرفی میدانیم در چنین خانوادهای احتمال انتخاب یک پسر از بین فرزندان برابر با و چنین احتمالی نیز برای دخترها برابر با است. حال اگر پیشامد A را انتخاب یکی از پسرها در بین فرزندان در نظر بگیریم، بخت برای چنین پیشامدی برابر است با:
و برعکس اگر بخت (انتخاب یک دختر از بین فرزندان) را محاسبه کنیم، خواهیم داشت:
این عدد نشان میدهد که بخت انتخاب دختران دو برابر پسران است. همانطور که دیده میشود مقدار بخت متفاوت از احتمال است زیرا در اینجا برای مثال مقدار بخت، بزرگتر از ۱ بدست آمده است.
رگرسیون لجستیک و رگرسیون خطی
حال به تعریف رگرسیون برمیگردیم. میدانیم که منظور از رگرسیون خطی، ایجاد رابطهای خطی برحسب پارامتر برای نمایش ارتباط بین متغیر مستقل و وابسته است. فرم مدل رگرسیون خطی ساده به صورت زیر است:
همانطور که دیده میشود این رابطه، معادله یک خط است که جمله خطا یا همان به آن اضافه شده. پارامترهای این مدل خطی، عرض از مبدا () و شیب خط () هستند. در این حالت اگر مقدار برآورد برای متغیر وابسته باشد، میتوان آن را میانگین مشاهدات برای متغیر وابسته به ازای مقدار ثابت متغیر مستقل در نظر گرفت. پس اگر میانگین را با امید ریاضی جایگزین کنیم با فرض اینکه میانگین جمله خطا نیز صفر است، خواهیم داشت:
که در آن نشاندهنده امید ریاضی (متوسط) شرطی است و همچنین و برآوردهای مربوط به هر یک از پارامترها هستند. اگر مقدار متغیر وابسته (Y)، باینری (دو وضعیتی) و شامل ۰ و ۱ باشد مشخص است که دارای توزیع برنولی است و امید ریاضی آن به صورت زیر محاسبه میشود:
به این ترتیب اگر بتوان برای تابع یک الگو در نظر گرفت، آنگاه مدل رگرسیون برای متغیر وابسته برنولی، مشخص میشود. با توجه به این تعریف، برآورد پارامترهای رگرسیون لجستیک را مشخص میکنیم.
برآورد پارامترهای رگرسیون لجستیک
از آنجایی که در بخش قبلی مقدار پیشبینی برای متغیر وابسته، با احتمال انجام شد، برای مشخص کردن مدل رابطه بین متغیر وابسته و مستقل به جای رابطه خطی، به تابعی احتیاج داریم که در حدود ۰ تا ۱ تغییر کند. در روش رگرسیون لجستیک از تابعی به نام «تابع لجستیک» (Logistic Function) استفاده میشود. به همین علت این روش رگرسیونی را رگرسیون لجستیک مینامند.
در ادامه این تابع معرفی و نمودار مربوط به آن براساس پارامترهای , در تصویر دیده میشود.
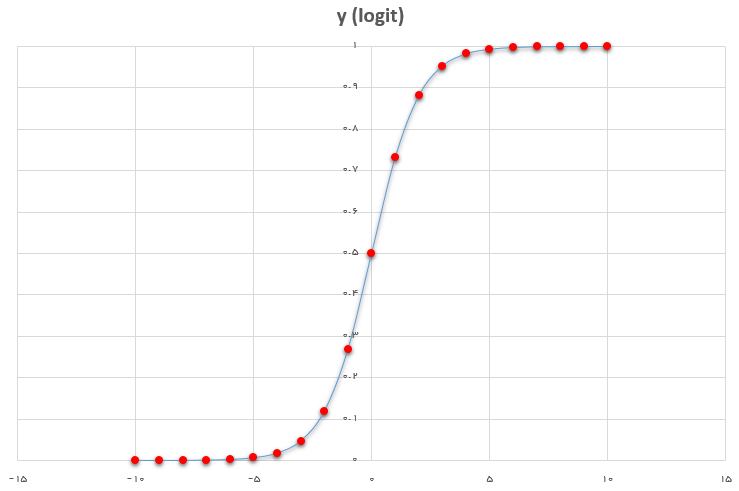
همانطور که دیده میشود با افزایش مقدار x () تابع لجستیک به ۱ نزدیک خواهد شد. همچنین با کاهش مقدار x () مقدار تابع به سمت صفر میل میکند. حال فرض کنید برای رگرسیون لجستیک از این تابع برای بیان احتمال متغیر وابسته استفاده شود. پس خواهیم داشت:
به منظور برآورد پارامترهای این مدل، میتوان از «تبدیل لوجیت» (Logit Transformation) استفاده کرد. این تبدیل را روی بخت که قبلا بیان شده، اجرا میکنیم. در این صورت رابطه را میتوان به شکل زیر نوشت:
با استفاده از تابع درستنمایی و حداکثر سازی آن میتوان مدل را براساس برآورد پارامترها بدست آورد. با این کار به یک دستگاه معادلات میرسیم که متاسفانه برای حل آن روش تحلیلی وجود ندارد و باید به کمک روشهای عددی برآورد را انجام داد. خوشبختانه نرمافزارهای زیادی از جمله SPSS قادر هستند که محاسبات و برآوردهای مربوط به رگرسیون لجستیک را انجام دهند و پارامترهای و را محاسبه کنند. در ادامه به بررسی یک مثال به کمک نرمافزار SPSS میپردازیم.
مثال
از ۲۰ دانشجو خواسته شده که در ابتدای روز اسمی را به خاطر بسپارند. زمان خواب شبانه بر حسب دقیقه و همچنین موفقیت یا عدم موفقیت در یادآوری اسم در صبح فردا در جدول زیر آورده شده است. با استفاده از رگرسیون لجستیک سعی میکنیم الگو یا مدلی برای میزان خواب و احتمال یادآوری موفق بیابیم. بهتر است ابتدا ارتباط بین این دو متغیر را بسنجیم.
| زمان خواب | 30 | 45 | 60 | 75 | 90 | 105 | 105 | 120 | 135 |
| یادآوری | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| زمان خواب | 150 | 165 | 180 | 195 | 210 | 240 | 255 | 270 | 285 |
| یادآوری | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| زمان خواب | 300 | 330 | دادههای مریوط به یادآوری اسم با توجه به میزان خواب برحسب دقیقه | ||||||
| یادآوری | 1 | 1 | |||||||
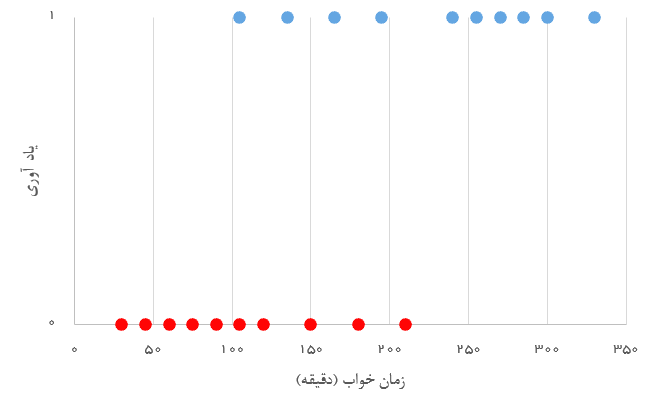
اگر نمودار نقطهای مربوط به این دادهها را ترسیم کنیم، خواهیم دید که با افزایش میزان خواب، سطح یادآوری از مقدار ۰ به ۱ تغییر میکند. هرچند این نمودار پیوسته نیست ولی میتوان ارتباط بین دو متغیر مستقل و وابسته را براساس آن مشاهده کرد.
برای اجرای رگرسیون لجستیک، دادهها به صورت زیر در صفحه ویرایشگر نرمافزار SPSS ثبت شدهاند. در همین راستا و با توجه به باینری بودن مقدارهای مربوط به متغیر وابسته از فهرست Analysis، گزینه Regression و دستور Binary Logistic را اجرا میکنیم.
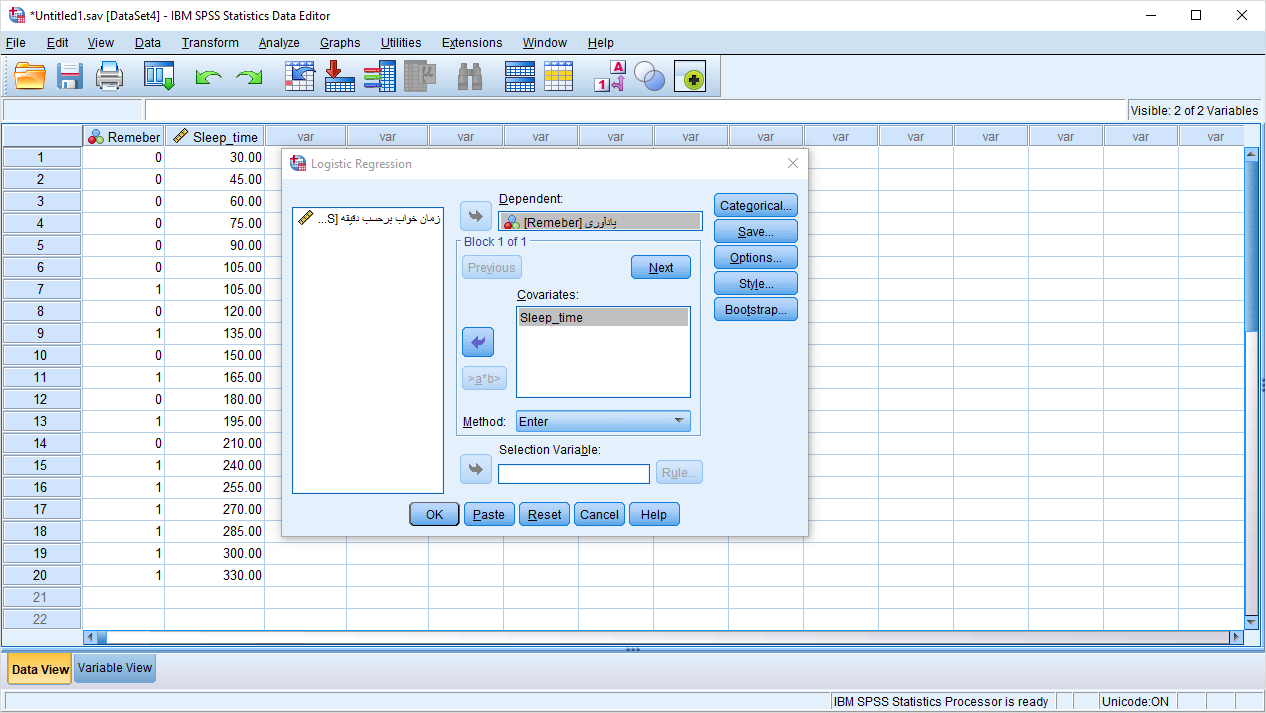
نکته: اگر متغیر وابسته یک متغیر گروهبندی با سطوح مقداری بیش از دو حالت باشد، از دستور Multinomial Logistic استفاده میکنیم.
خروجی حاصل از این دستور نیز در تصویر زیر قابل مشاهده است. در انتهای این خروجی دو جدول با نامهای Classification Table و Variables in Equation قرار دارند که اولی نتیجه دستهبندی و دومی پارامترهای مدل را نشان میدهد. همانطور که در جدول اول در قسمت Overall Percentage میبینید، ۸۰٪ دستهبندی مشاهدات توسط مدل در گروه صحیح قرار گرفتهاند و مدل دارای ۲۰ درصد خطا است. یعنی کسانی که عمل یادآوری را به درستی انجام ندادهاند ۸۰٪ صحیح تشخیص داده شدهاند و در مقابل کسانی که عمل یادآوری را به درستی اجرا کردهاند نیز ۸۰٪ پیشبینی شدهاند. بنابراین مدل، مناسب به نظر میرسد.
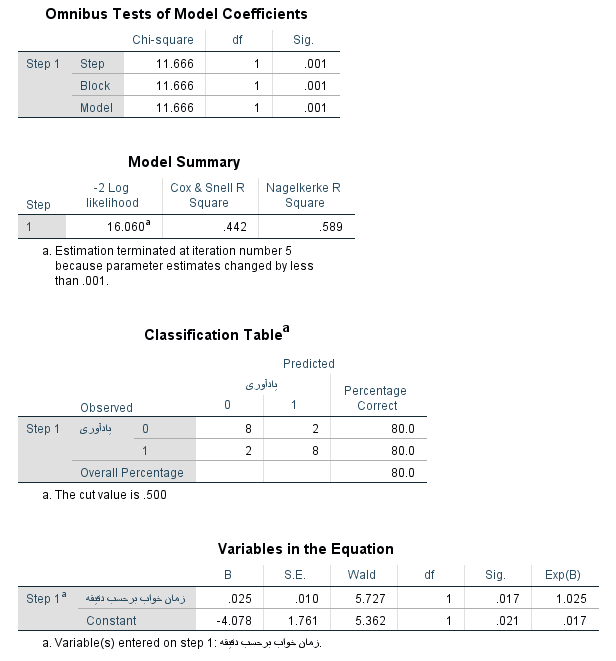
همچنین در جدول دوم که پارامترهای مدل را نشان میدهد، برآورد پارامترهای آن به صورت و خواهد بود. بنابراین احتمال اینکه فردی پس از x ساعت خواب بتواند اسم مورد نظر را به یاد بیاورد طبق تابع زیر محاسبه میشود.
برای هر یک از پارامترها، مقدار احتمال (p-value) نیز که در ستون sig دیده میشود کمتر از 0.05 است. در نتیجه فرض صفر بودن این پارامترها رد میشود و از همین رو میتوان مدل را مناسب یافت. میتوانید با انتخاب گزینه Save در پنجره Logistic Regression، مقدار تابع احتمال مدل رگرسیون لجستیک (Probabilities) را به ازای Y=1 محاسبه کنید. همچنین امکان ظاهر کردن برچسب تعلق هر مشاهده به گروهها (Group membership) را نیز دارید. کافی است تنظیمات پنجره Save را به صورت زیر انجام دهید.
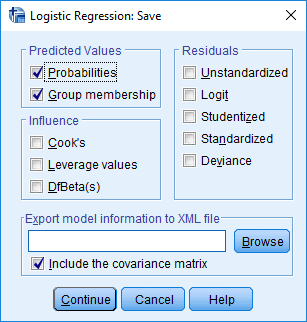
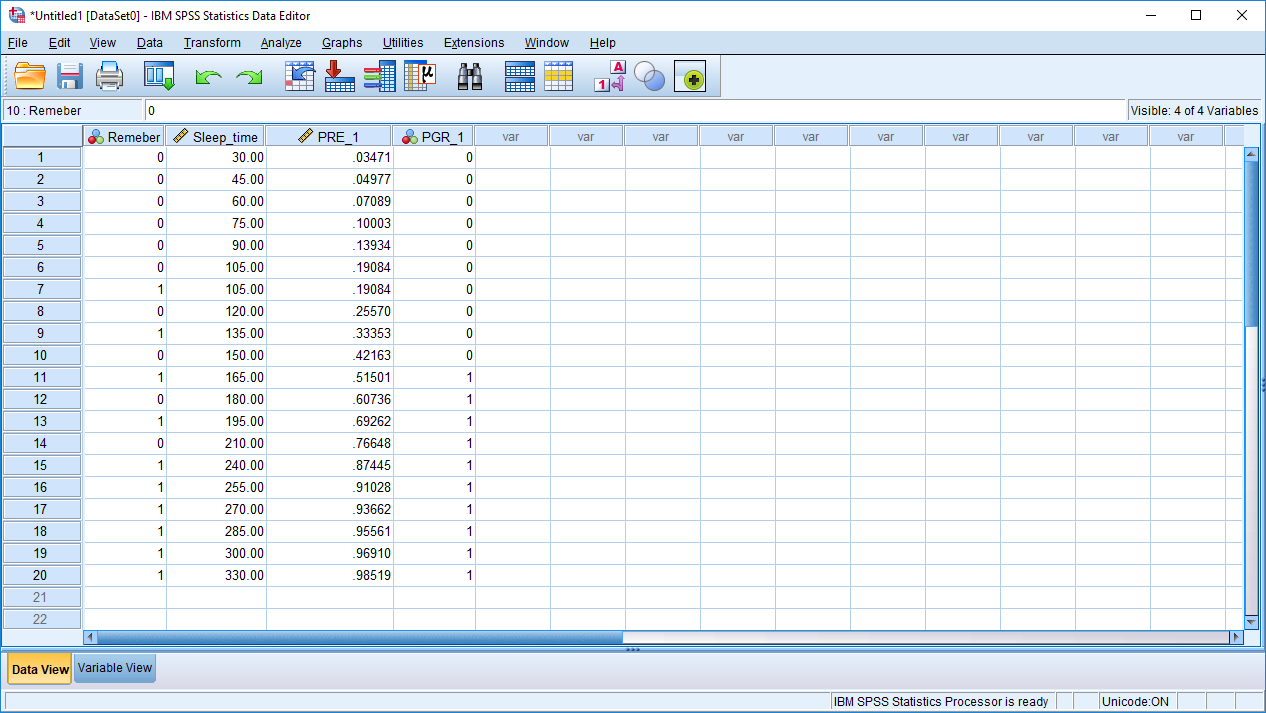
به این ترتیب این مقدارها در جدول دادههای SPSS قابل مشاهدهاند. ستون PRE_1 بیانگر پیشبینی مقدار احتمال و PGR_1 نیز نشانگر دستهای است که مشاهده به آن تعلق دارد. همانطور که دیده میشود مشاهدهای که مقدار احتمال برای آن بزرگتر از 0.5 باشد در دسته یا گروه ۱ جای میگیرد و در غیر اینصورت در گروه ۰ باقی میماند.
معرفی فیلم آموزش تحلیل رگرسیون لجستیک دو حالتی در SPSS
مدل «رگرسیون لجستیک» (Logistic Regression) یا بخصوص در «یادگیری ماشین» (Machine Learning) در زمینه «دستهبندی» (Classification) کاربرد زیادی دارد. این تکنیک آماری بدون در نظر گرفتن توزیع نرمال برای دادهها یا متغیرهای پیشگو، مقادیر متغیر رستهای (دو دویی) را پیشبینی میکند. یکی از آموزشهای کاربردی فرادرس نیز به رگرسیون لجستیک با نرمافزار SPSS اختصاص دارد. این فیلم آموزشی علاوه بر ذکر مثالهای کاربردی، مبانی نظری و همچنین فرمولها و محاسبات مورد نظر را معرفی میکند. همچنین در بخشی از این آموزش، تکنیکها یا روشهای اندازهگیری و نمایش خطای دستهبندی و نمودار ROC یا (Receiver Operation Characteristic) را معرفی میکند.
استفاده از نرمافزار SPSS برای پیادهسازی رگرسیون لجستیک و انجام محاسبات مربوطه به این آموزش غنای بیشتری بخشیده است. این آموزش شامل حدود یک ساعت و چهارده دقیقه است که در آن سرفصلهای آموزشی طبق فهرست زیر است.
- درس یکم : ابتدا، مقدمه بر تحلیل رگرسیون، رگرسیون لجستیک و رگرسیون لجستیک ساده در نرم افزار SPSS صورت گرفته و مثالهایی برای آشنایی نحوه عملکرد رگرسیون لجستیک مرور میشود. «نسبت بخت» (Odd Ratio)، همچنین «آزمون کلینگر» (Omni test) و «مدل رگرسیون ساده» (Simple Regression Model) نیز مورد بررسی قرار میگیرد. شاخصهای منفی و مثبت کاذب (False/Negative - False/Positive)، منفی و مثبت صحیح (True/Negative - True / Positive) نیز از مواردی هستند که در درس یکم به آن پرداخته شده است.
- درس دوم: انجام تحلیل رگرسیون لجستیک چندگانه، با توجه به چند متغیر صورت گرفته و مدلهای آشیانی و آزمون باکس-تیدول نیز معرفی میشوند. در انتها، نحوه رسم نمودار ROC و تهیه خروجی از نرمافزار SPSS آورده شده است. گزارش نویسی و تفسیر نتایج حاصل از اجرای مدل رگرسیونی از مواردی است که در درس دوم قابل مشاهده است.
این آموزش براساس یکی از بهترین کتابهای لاتین به نام «رگرسیون لجستیک کاربردی» (Applied Logistic Regression) در این زمینه، تدریس و تهیه شده و برای محققین در حوزه علوم پزشکی، علوم اجتماعی، آمار و مدیریت مناسب است. آشنایی اولیه با مفاهیم آماری و همچنین آگاهی از نحوه کار با محیط نرمافزاری SPSS از پیشنیازهای این فیلم آموزشی محسوب میشود.
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزش های SPSS
- مجموعه آموزش های داده کاوی یا Data Mining در متلب
- آموزش همبستگی و رگرسیون خطی در SPSS
- مهمترین الگوریتمهای یادگیری ماشین (به همراه کدهای پایتون و R) — بخش دوم: رگرسیون خطی
- آموزش یادگیری ماشین
- مجموعه آموزشهای نرمافزارهای آماری
- ضریبهای همبستگی (Correlation Coefficients) و شیوه محاسبه آنها
- مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری
^^