توابع چند متغیره — به زبان ساده

در مطالب ارائه شده در وبلاگ فرادرس در مورد حد، مشتق و انتگرال صحبت شد. مفاهیم مذکور پایه‌های اصلی حساب دیفرانسیل را تشکیل می‌دهند. تمامی مفاهیم یاد شده مبتنی بر توابع تک متغیره هستند. واقعیت این است که هدف اصلی ریاضیات توضیح پدیده‌های فیزیکی است. اما نکته این‌جا است که در طبیعت، اکثر تغییرات به چندین عامل وابسته است. این پدیده‌ها را می‌توان با استفاده از موجوداتی به نام «تابع چند متغیره» (Multivariable Function) توصیف کرد. در بخش‌های آینده در مورد نحوه پیاده‌سازی مفاهیم پایه‌ای (هم‌چون مشتق و انتگرال) روی این توابع نیز بحث خواهیم کرد.

به چه تابعی چند متغیره گفته می‌شود؟

از ریاضیات پایه می‌دانیم که یک تابع عبارت است از دستگاهی که ورودی را دریافت می‌کند و خروجی را تحویل می‌دهد. برای نمونه تابع f(x)=x²+1 را در نظر بگیرید. رابطه مفروض، x را دریافت می‌کند و x²+1 را تحویل می‌دهد. با این فرض ماکروفر نیز یک تابع است چرا که یک غذای سرد را به عنوان x دریافت می‌کند و خروجی آن غذای گرم یا همان (f(x است.

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

احتمالا از ماکروفر استفاده کرده‌اید. در هنگام قرار دادن غذا در آن می‌توانیم دمای محیط درونی‌اش و مدت زمان دلخواه جهت گرم شدن غذا را انتخاب کنیم. در حقیقت ورودی تابع ماکروفر دو پارامتر زیر است.

1. مدت زمان تنظیم شده جهت گرم کردن غذا
2. دمای تنظیم شده ماکروفر

بنابراین دمای غذای خروجی به دو پارامتر بالا وابسته است. از این رو می‌توان گفت:

دمای غذای خروجی = f (دمای تنظیم شده جهت گرم شدن و مدت زمان گرم شدن غذا)

در نتیجه ماکروفر تحت چنین شرایطی هم‌چون تابعی دو متغیره عمل می‌کند. به تابعی چند متغیره گفته می‌شود که در ورودی آن چندین عدد باشد. برای نمونه به‌منظور محاسبه تابع زیر به دو عدد x و y نیاز داریم.

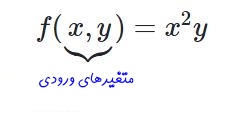
توجه داشته باشید که در بعضی از مواقع خروجی تابع می‌تواند از دو یا چند عدد تشکیل شده باشد. به چنین توابعی نیز چند متغیره گفته می‌شود. معمولا این موجودات را توابع برداری می‌نامند. در ادامه نمونه‌ای از یک تابع برداری نشان داده شده است.

بنابراین به شکلی دقیق‌تر می‌توان گفت تابع چند متغیره موجودی است که ورودی، خروجی و یا هر دوی آن‌ها از دو یا چند عدد تشکیل شده باشد. تنها به تابعی تک متغیره گفته می‌شود که از یک ورودی و یک خروجی تشکیل شده باشد.

معمولا برای فهم توابع چند‌ متغیره، بایستی از فضاهای دو یا چند بعدی درک واضحی داشت. در حقیقت در این توابع، هر عدد نشان دهنده یک بعد است. در جدول زیر دسته‌بندی توابع مختلف به‌همراه مثالی از هرکدام نشان داده شده است. لطفا جدول زیر را مورد توجه قرار دهید.

مثال‌هایی از توابع چند متغیره

هر‌چه بیشتر در مورد پدیده‌های فیزیکی اطراف خود دقت کنید، متوجه می‌شوید که اکثر آن‌ها را نمی‌توان با استفاده از توابع تک متغیره مدل‌سازی کرد. در این‌جا به تعدادی تابع چند متغیره اشاره خواهیم کرد.

فیلم آموزش ریاضی عمومی ۲ در فرادرس

کلیک کنید

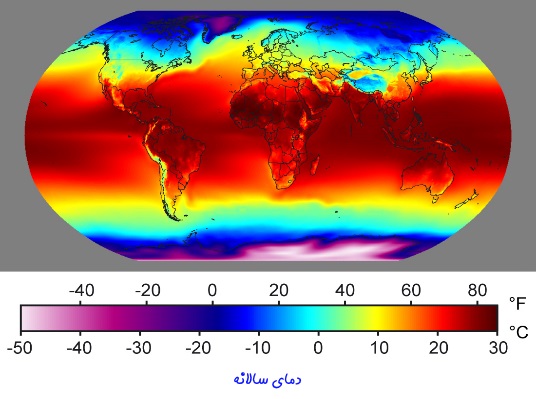
مثال ۱: رابطه دما با مکان

به‌منظور بیان دمای یک نقطه از کره زمین به مختصات طولی، عرضی و حتی ارتفاع نیازمند هستید. بنابراین دمای یک نقطه را می‌توان به شکل زیر بیان کرد:

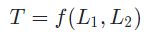
• T: دمای نقطه مشخص شده
• L₁: مختصات طولی
• L₂: محتصات عرضی

بنابراین می‌توان گفت کمیت دما وابسته به دو متغیرِ مختصات طولی و عرضی است.

مثال۲: وابستگی مختصات ذره به زمان

به‌منظور مدل‌سازی حرکت یک ذره در فضا و زمان می‌توان از تابعی سه‌متغیره استفاده کرد. در حقیقت کمیت‌های x ،y ،t توصیف‌ کننده مسیر حرکت ذره هستند. به طور دقیق‌تر می‌توان گفت مسیر حرکت ذره مفروض در قالب یک بردار توصیف می‌شود. اگر این بردار را با $$\overrightarrow {s}$$ نشان دهیم، می‌توان گفت:

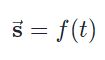
• $$\overrightarrow {s}$$ برداری سه متغیره است که موقعیت ذره در زمان را نشان می‌دهد.
• t معادل با زمان است.
• f تابعی برداری است.

در بعضی مواقع می‌توان مولفه‌های بردار موقعیت را به شکلی جداگانه و بر حسب زمان بیان کرد. در حقیقت می‌توان گفت:

x(t)= (t عبارتی بر حسب )

y(t)= (t عبارتی بر حسب )

مثال ۳: بازخورد کاربران یک وبسایت با استفاده از داده‌ها

زمانی که یک وبسایت می‌خواهد رفتار کاربران خود را پیش‌بینی کند، توابعی تعریف می‌کند که با استفاده از آن‌ها می‌تواند هزاران پارامتر را از کاربران خود دریافت کند. نمونه‌ای از این پارامترها می‌تواند سن، تحصیلات، تعداد کلیک‌های آن‌ها روی یک لینک خاص و ... باشد. با توجه به این ورودی‌ها، خروجی نیز می‌تواند شامل کمیت‌هایی مثل احتمال کلیک آن‌ها روی لینک دیگری یا خرید کالای خاصی باشد.

مثال۴: محاسبه بردار سرعت با استفاده از بردار مکان

اگر شما به دنبال مدل‌سازی سیالی خاص اطراف یک جسم هستید، یک راه می‌تواند بیان کردن سرعت هریک از ذرات سیال باشد. برای این کار تابعی را فرض کنید که ورودی آن، بردار مکان یک ذره و خروجی آن، سرعت سیال باشد.

فیلم آموزش ریاضی عمومی ۲ + حل مثال در فرادرس

کلیک کنید

برای نشان دادن چنین تابعی راه‌های زیادی وجود دارد. برای نمونه می‌توان آن را به صورت زیر بیان کرد:

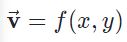
اجزاء رابطه بالا به ترتیب زیر برابر هستند با:

$$\overrightarrow {v}$$: بردار سرعتِ دو بعدی

x و y: مختصات مکانی

f: تابع برداری چند متغیره

هم‌چنین می‌توان این تابع را به شکل بردار نشان داد و از نماد‌های $$\widehat {i},\widehat {j}$$ مطابق با رابطه زیر بهره برد.

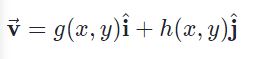
$$\overrightarrow {v}$$: بردار سرعت دو بعدی

$$\widehat {i}$$: بردار واحد در راستای x

$$\widehat {j}$$: بردار واحد در راستای y

g: تابع اسکالرِ توصیف کننده موقعیت x ذره در زمان

h: تابع اسکالرِ توصیف کننده موقعیت y ذره در زمان

برای نمونه شکل زیر نمودارِ تابعی برداری و چند متغیره را نشان می‌دهد. با دقت در آن می‌بینید که اندازه و جهت بردار سرعت با توجه به مکان ذره متفاوت است.

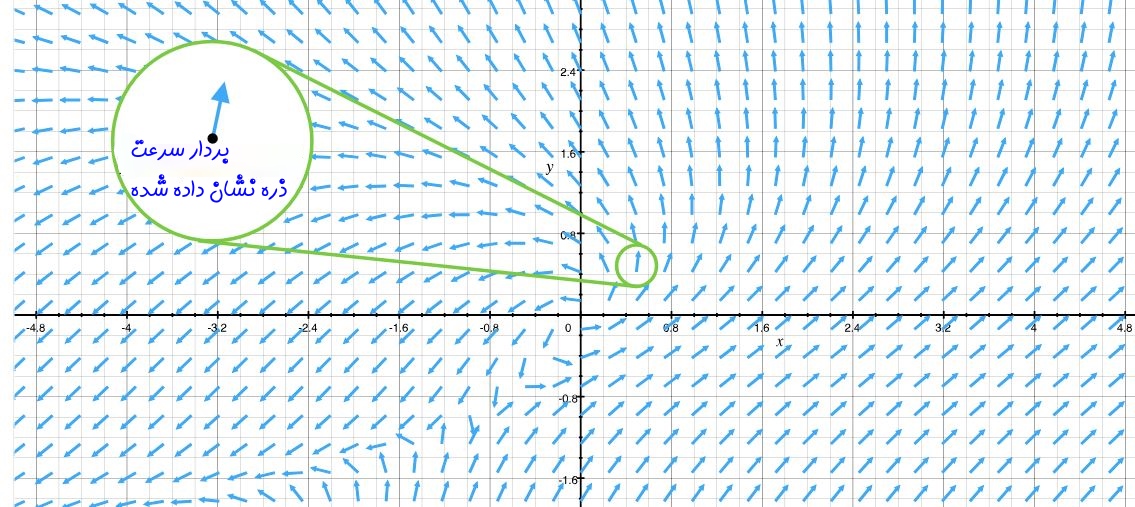
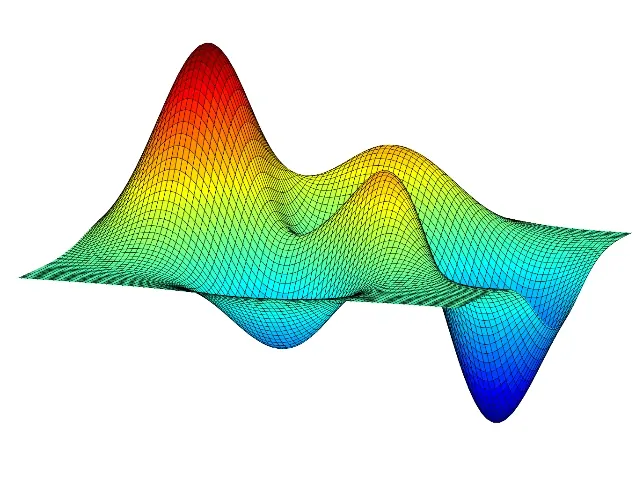
توابع چند متغیره نشان دهنده صفحه و یا حجم در فضا هستند. مثالی که در ادامه آمده تابعی را نشان می‌دهد که توصیف کننده یک صفحه در فضا است.

مثال ۵:‌ $$f(x,y)= \sqrt {x} + \sqrt {y}$$

تابع بالا رابطه‌ای سه‌بعدی را نشان می‌دهد که در آن f یا همان z به x,y وابسته است. با توجه به این‌که f دو وابسته دارد، در نتیجه این تابع چند‌متغیره محسوب می‌شود. چنین تابعی در حقیقت نشان دهنده یک رویه در فضای سه‌بعدی است. در شکل زیر نمایی از این تابع را می توانید ببینید.

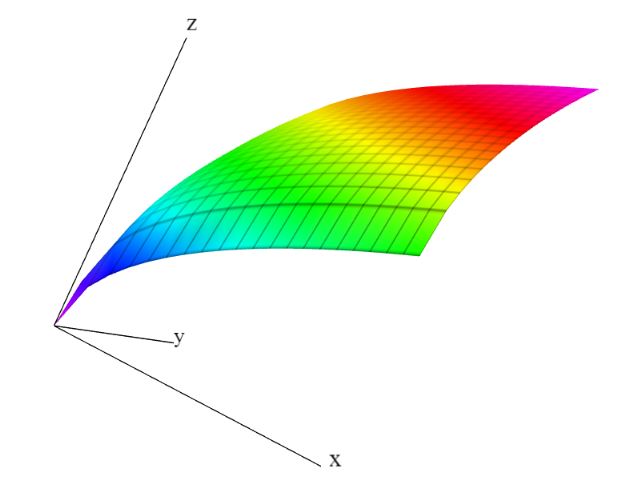
فهم توابع چند متغیره از این جهت ضروری است که پیش‌نیاز مبحث مهمی تحت عنوان معادلات دیفرانسیل با مشتقات جزئی (Partial Differential Equation) است. از این رو برای درک بهتر این مطلب می‌توانید به این آموزش مراجعه کنید.

هم‌چنین در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضیات، احتمالا آموزش‌های زیر برایتان کاربردی خواهند بود:

• مجموعه آموزش‌های ریاضیات به صورت گام به گام
• مجموعه آموزش‌های ریاضی و فیزیک
• آموزش ریاضی عمومی ۱ (حل مثال و تست کنکور کارشناسی و ارشد)
• روش‌های مشتق‌گیری — به همراه مثال
• مفاهیم انتگرال — به زبان ساده

^^