سری توانی — به زبان ساده (+ دانلود فیلم آموزش رایگان)

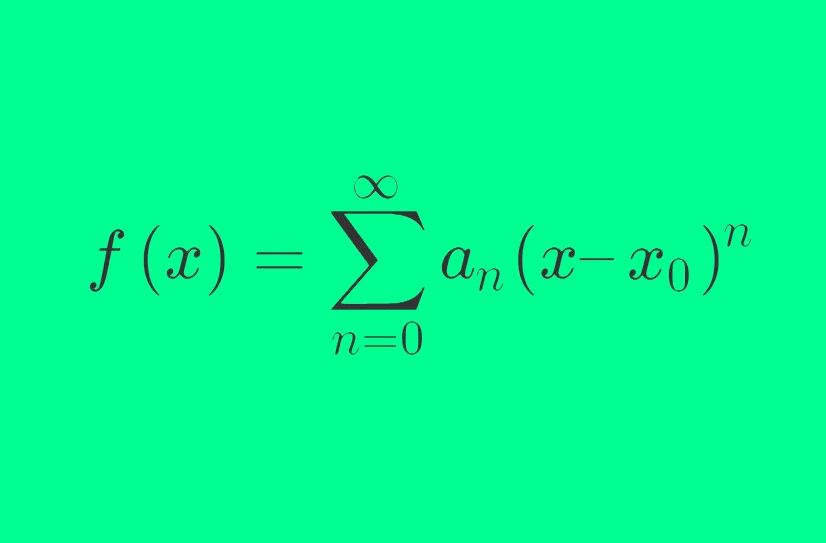
در مباحث قبلی مجله فرادرس، حل معادلات دیفرانسیل با استفاده از روش‌ سری توانی را بیان کردیم و دیدیم که سری توانی، کاربرد بسیار مهمی در حل معادلات دیفرانسیل دارد. در این آموزش از مجموعه آموزش‌های مجله فرادرس، درباره موضوعات مربوط به سری‌های توانی بحث خواهیم کرد.

معرفی سری توانی

شکل کلی یک سری توانی به‌صورت زیر است:

$$\begin{equation}f\left( x \right) = \sum\limits_{n = 0}^\infty {{a_n}{{\left( {x - {x_0}} \right)}^n}} \label{eq:eq1}\end{equation}$$

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

که در آن، $$x_0$$ و $$a_n$$ اعداد ثابتی هستند. بنابراین، سری توانی تابعی از $$x$$ است. نماد تابع ($$f(x)$$) را همیشه در کنار سری نمی‌نویسند، اما گاهی اوقات، تعریف بالا را به کار می‌بریم.

قبل از توضیح درباره جزئیات سری توانی، ابتدا باید آن را به‌صورت مجموع تک‌تک جملات آن بنویسیم. سری تونی را می‌توان به‌صورت زیر نوشت:

$$\begin{equation}\begin{aligned}f\left( x \right) &= \sum\limits_{n = 0}^\infty {{a_n}{{\left( {x - {x_0}} \right)}^n}} \\ & = {a_0} + {a_1}\left( {x - {x_0}} \right) + {a_2}{\left( {x - {x_0}} \right)^2} + {a_3}{\left( {x - {x_0}} \right)^3} + \cdots \end{aligned}\label{eq:eq2}\end{equation}$$

البته به دلایلی، سری توانی را به‌شکل زیر نیز می‌نویسیم:

$$\begin{align*}f\left( x \right) &= \sum\limits_{n = 0}^\infty {{a_n}{{\left( {x - {x_0}} \right)}^n}} \\ & = {a_0} + {a_1}\left( {x - {x_0}} \right) + {a_2}{\left( {x - {x_0}} \right)^2} + {a_3}{\left( {x - {x_0}} \right)^3} + \cdots \\ & = {a_0} + \sum\limits_{n = 1}^\infty {{a_n}{{\left( {x - {x_0}} \right)}^n}} \end{align*}$$

نوشتن سری توانی به‌صورت بالا، به این خاطر است که اگر از جمله اول ($$n=0$$) چشم‌پوشی کنیم، سایر جملات، یک سری هستند که از $$n=1$$ شروع می‌شوند. با این کار، جمله نخست را جدا کرده‌ایم. جدا کردن بخشی از سری، محدود به جمله اول نیست. برای مثال، می‌توانیم سه جمله اول را به‌صورت زیر، از سری جدا کنیم:

$$\sum\limits_{n = 0}^\infty {{a_n}{{\left( {x - {x_0}} \right)}^n}} = {a_0} + {a_1}\left( {x - {x_0}} \right) + {a_2}{\left( {x - {x_0}} \right)^2} + \sum\limits_{n = 3}^\infty {{a_n}{{\left( {x - {x_0}} \right)}^n}}$$

همگرایی سری

از آن‌جایی که سری‌های توانی تابعی از $$x$$ هستند و می‌دانیم در واقعیت هر سری را نمی‌توان با یک مقدار یا عبارت مشخص بیان کرد، این پرسش پیش می‌آید که آیا یک سری توانی برای همه مقادیر $$x$$ وجود دارد؟ این پرسش را می‌توان با توجه به همگرایی سری توانی پاسخ داد.

فیلم آموزش ریاضی پایه – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

می‌گوییم یک سری توانی به‌ازای $$x=c$$ همگرا است، اگر سری زیر همگرا باشد:

$$\sum\limits_{n = 0}^\infty {{a_n}{{\left( {c - {x_0}} \right)}^n}}$$

همچنین، این سری همگرا خواهد بود، اگر حد مجموع جزئی زیر، محدود باشد:

$$\mathop {\lim }\limits_{N \to \infty } \sum\limits_{n = 0}^N {{a_n}{{\left( {c - {x_0}} \right)}^n}}$$

به‌عبارت دیگر، یک سری توانی به‌ازای $$x=c$$ همگراست، اگر حاصل عبارت زیر، یک عدد محدود (غیربی‌نهایت) باشد.

$$\sum\limits_{n = 0}^\infty {{a_n}{{\left( {c - {x_0}} \right)}^n}}$$

لازم به ذکر است که اگر $$x=x_0$$ باشد، یک سری توانی همیشه همگرا است.

برای سری توانی $$f\left( x \right) = \sum\limits_{n = 0}^\infty {{a_n}{{\left( {x - {x_0}} \right)}^n}}$$، عدد $$0\le\rho\le\infty$$ وجود خواهد داشت که سری توانی به‌ازای $$\left | {x - {x_0}} \right | < \rho$$ همگرا و به‌ازای $$\left | {x - {x_0}} \right | > \rho$$ واگرا خواهد شد. این عدد، شعاع همگرایی نامیده می‌شود.

آزمون نسبت، روشی است که با استفاده از آن می‌توان شعاع همگرایی اغلب سری‌های توانی را به سادگی تعیین کرد.

آزمون نسبت

اگر عبارت زیر را برای یک سری توانی محاسبه کنیم:

$$L = \left| {x - {x_0}} \right|\mathop {\lim }\limits_{n \to \infty } \left| {\frac{{{a_{n + 1}}}}{{{a_n}}}} \right|$$

آن‌گاه داریم:

• $$\hspace{0.25in} \Leftarrow L<1$$ سری همگرا است.
• $$\hspace{0.25in} \Leftarrow L>1$$ سری واگرا است.
• $$\hspace{0.25in} \Leftarrow L=1$$ سری ممکن است همگرا یا واگرا باشد.

مثال

شعاع همگرایی سری توانی زیر را تعیین کنید.

$$\sum\limits_{n = 0}^\infty {\frac{{{{\left( { - 3} \right)}^n}}}{{n\,{7^{n + 1}}}}{{\left( {x - 5} \right)}^n}}$$

حل: جملات $$a_n$$ و $$a_{n+1}$$ این سری، به‌شکل زیر هستند:

$${a_n} = \frac{{{{\left( { - 3} \right)}^n}}}{{n\,{7^{n + 1}}}}\hspace{0.25in}{a_{n + 1}} = \frac{{{{\left( { - 3} \right)}^{n + 1}}}}{{\left( {n + 1} \right)\,{7^{n + 2}}}}$$

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

حال، از آزمون نسبت استفاده می‌کنیم. بنابراین، داریم:

$$\begin{align*}L & = \left| {x - 5} \right|\mathop {\lim }\limits_{n \to \infty } \left| {\frac{{{a_{n + 1}}}}{{{a_n}}}} \right|\\ & = \left| {x - 5} \right|\mathop {\lim }\limits_{n \to \infty } \left| {\frac{{{{\left( { - 3} \right)}^{n + 1}}}}{{\left( {n + 1} \right)\,{7^{n + 2}}}}\,\,\frac{{n\,{7^{n + 1}}}}{{{{\left( { - 3} \right)}^n}}}} \right|\\ & = \left| {x - 5} \right|\mathop {\lim }\limits_{n \to \infty } \left| {\frac{{ - 3}}{{\left( {n + 1} \right)\,7}}\,\,\frac{n}{1}} \right|\\ & = \frac{3}{7}\left| {x - 5} \right|\end{align*}$$

از عبارت بالا می‌توان دریافت که سری همگرا خواهد بود، اگر:

$$\frac{3}{7}\left| {x - 5} \right| < 1\hspace{0.25in} \Rightarrow \hspace{0.25in}\left| {x - 5} \right| < \frac{7}{3}$$

و سری واگراست اگر:

$$\frac{3}{7}\left| {x - 5} \right| > 1\hspace{0.25in} \Rightarrow \hspace{0.25in}\left| {x - 5} \right| > \frac{7}{3}$$

به عبارت دیگر، شعاع همگرایی این سری، برابر است با:

$$\rho = \frac{7}{3}$$

همان‌گونه که در مثال بالا دیدیم، شعاع همگرایی به‌سادگی و با استفاده از آزمون نسبت به‌دست آمد.

اما چرا همگرایی سری‌های توانی مهم است؟ پاسخ این است که برای آنکه از سری برای حل یک معادله دیفرانسیل در یک $$x$$ خاص استفاده کنیم، به همگرایی سری در $$x$$ نیاز داریم. اگر در یک $$x$$‌ داده شده همگرایی وجود نداشته باشد، آن‌گاه حل سری در آن $$x$$ وجود نخواهد داشت. بنابراین، همگرایی سری توانی بسیار مهم ست.

خواص سری توانی

در ادامه، چند مورد از خواص و عملیات روی سری توانی را بررسی خواهیم کرد. ابتدا از جمع و تفریق شروع می‌کنیم.

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

جمع و تفریق عملیات ساده‌ای روی سری‌های توانی است و چیز زیادی برای گفتن درباره آن وجود ندارد. فقط باید توجه کنیم که نقطه شروع و پایان سری‌ها و توان مربوط به پایه $$x-x_0$$ آن‌ها برابر باشد. با این اوصاف، می‌توان جمع و تفریق سری‌های توانی را به‌صورت زیر نوشت:

$$\sum\limits_{n = {n_0}}^\infty {{a_n}{{\left( {x - {x_0}} \right)}^n}} \pm \sum\limits_{n = {n_0}}^\infty {{b_n}{{\left( {x - {x_0}} \right)}^n}} = \sum\limits_{n = {n_0}}^\infty {\left( {{a_n} \pm {b_n}} \right){{\left( {x - {x_0}} \right)}^n}}$$

به عبارت دیگر، با جمع ضرایب سری‌ها، به سری‌های جدید می‌رسیم.

یکی از قواعدی که هنگام پیدا کردن حل معادلات دیفرانسیل با آن سروکار داریم، این است که آن $$x$$ی که در یک سری لازم داریم، همانی است که در $$(x-x_0)^n$$ جای داده شده است. این بدین معنی است که متغیر $$x$$ را باید به داخل سری منتقل کنیم و قادر باشیم با سری‌هایی به فرم زیر کار کنیم (آن‌ها را به فرم اصلی برگردانیم):

$${\left( {x - {x_0}} \right)^c}\sum\limits_{n = 0}^\infty {{a_n}{{\left( {x - {x_0}} \right)}^n}}$$

که در آن، $$c$$ عددی ثابت است. در حقیقت، به‌سادگی داریم:

$$\begin{align*}{\left( {x - {x_0}} \right)^c}\sum\limits_{n = 0}^\infty {{a_n}{{\left( {x - {x_0}} \right)}^n}} & = {\left( {x - {x_0}} \right)^c}\left( {{a_0} + {a_1}\left( {x - {x_0}} \right) + {a_2}{{\left( {x - {x_0}} \right)}^2} + \cdots } \right)\\ & = {a_0}{\left( {x - {x_0}} \right)^c} + {a_1}{\left( {x - {x_0}} \right)^{1 + c}} + {a_2}{\left( {x - {x_0}} \right)^{2 + c}} + \cdots \\ & \sum\limits_{n = 0}^\infty {{a_n}{{\left( {x - {x_0}} \right)}^{n + c}}} \end{align*}$$

بنابراین، می‌توانیم چندجمله‌ای را با پایه مشترک در سری ضرب کرده و در نهایت توان آن‌ها را با هم جمع کنیم.

گاهی لازم است از سری توانی مشتق بگیریم. با بسط سری به جمله‌های آن، مشتق‌گیری به‌آسانی انجام می‌شود. بنابراین، مشتق یک سری توانی به‌صورت زیر است:

$$\begin{align*}f'\left( x \right) & = {a_1} + 2{a_2}\left( {x - {x_0}} \right) + 3{a_3}{\left( {x - {x_0}} \right)^2} + \cdots \\ & = \sum\limits_{n = 1}^\infty {n{a_n}{{\left( {x - {x_0}} \right)}^{n - 1}}} \\ & = \sum\limits_{n = 0}^\infty {n{a_n}{{\left( {x - {x_0}} \right)}^{n - 1}}} \end{align*}$$

بنابراین، کافی است از عبارت داخل سری مشتق بگیریم. از آن‌جایی که مشتق جمله متناظر با $$n=0$$ برابر با صفر است، مشتق سری را می‌توان از $$n=0$$ یا $$n=1$$ شروع کرد. معمولاًً سری را از $$n=1$$‌ شروع می‌کنیم. هرچند، گاهی در برخی مسائل برای سادگی لازم است از $$n=0$$‌ شروع کنیم.

مشتق دوم سری توانی، مانند مشتق اول و به‌صورت زیر محاسبه می‌شود:

$$\begin{align*}f''\left( x \right) & = \sum\limits_{n = 2}^\infty {n\left( {n - 1} \right){a_n}{{\left( {x - {x_0}} \right)}^{n - 2}}} \\ & = \sum\limits_{n = 1}^\infty {n\left( {n - 1} \right){a_n}{{\left( {x - {x_0}} \right)}^{n - 2}}} \\ & = \sum\limits_{n = 0}^\infty {n\left( {n - 1} \right){a_n}{{\left( {x - {x_0}} \right)}^{n - 2}}} \end{align*}$$

در این حالت، جملات مربوط به $$n=0$$ و $$n=1$$، هر دو صفر هستند و می‌توان سری را از سه نقطه ممکن شروع کرد.

یکی دیگر از عملیاتی که روی سری‌های توانی انجام می‌شود، جابه‌جایی یا تغییر اندیس است. گاهی اندیس از حداقل مقدار ممکن آغاز نمی‌شود و برای اینکه به فرم استاندارد مورد نیاز ما باشد، باید آن را به مقدار مورد نیاز تغییر دهیم. مثال زیر، این موضوع را به‌خوبی نشام می‌دهد:

مثال

سری زیر از مقدار $$n=3$$ شروع شده است. آن را به‌گونه‌ای بازنویسی کنید که از $$n=0$$‌ آغاز شود.

$$\sum\limits_{n = 3}^\infty {{n^2}{a_{n - 1}}{{\left( {x + 4} \right)}^{n + 2}}}$$

حل: با تغییرات ساده‌ای می‌توان اندیس را جابه‌جا کرد. ابتدا، اندیس جدید را به‌صورت $$i=n-3$$ تعریف می‌کنیم که اگر $$n=3$$‌ قرار دهیم، مقدار $$i=0$$‌ را خواهیم داشت. بنابراین، سری را برحسب $$i$$ بازنویسی می‌کنیم. این کار را با قرار دادن $$n=i+3$$ انجام می‌دهیم. در نتیجه، هر جایی که $$n$$ دیدیم، به‌جای آن، $$i+3$$‌ قرار می‌دهیم. اگر این جایگزینی را انجام دهیم، داریم:

$$\begin{align*}\sum\limits_{n = 3}^\infty {{n^2}{a_{n - 1}}{{\left( {x + 4} \right)}^{n + 2}}} & = \sum\limits_{i = 0}^\infty {{{\left( {i + 3} \right)}^2}{a_{i + 3 - 1}}{{\left( {x + 4} \right)}^{i + 3 + 2}}} \\ & = \sum\limits_{i = 0}^\infty {{{\left( {i + 3} \right)}^2}{a_{i + 2}}{{\left( {x + 4} \right)}^{i + 5}}} \end{align*}$$

توجه کنید که حد بالای سری تغییر نمی‌کند، زیرا اگر از بی‌نهایت، سه عدد کم شود، باز هم بی‌نهایت باقی می‌ماند.

در نتیجه می‌توان گفت تساوی زیر برقرار است:

$$\sum\limits_{n = 3}^\infty {{n^2}{a_{n - 1}}{{\left( {x + 4} \right)}^{n + 2}}} = \sum\limits_{n = 0}^\infty {{{\left( {n + 3} \right)}^2}{a_{n + 2}}{{\left( {x + 4} \right)}^{n + 5}}}$$

از مثال بالا به نتیجه‌ای کاربردی می‌رسیم و آن این است که برای جابه‌جایی اندیس می‌توانیم نقطه شروع سری را به اندازه مورد نظر کم کرده و اندیس‌های داخل سری را به همان اندازه زیاد کنیم. این کار برای افزایش مقدار شروع نیز صادق است. یعنی اگر بخواهیم شروع سری را به‌اندازه مشخصی زیاد کنیم، باید اندیس‌های داخل سری را به همان اندازه کاهش دهیم.

مثال

سری زیر را برای نقطه شروع $$n=5$$ به‌جای $$n=3$$ بازنویسی کنید.

$$\sum\limits_{n = 3}^\infty {{n^2}{a_{n - 1}}{{\left( {x + 4} \right)}^{n + 2}}}$$

حل: برای شروع شدن سری از $$n=5$$، باید اندیس‌های داخل سری را به‌اندازه ۲ واحد کم کنیم (زیرا شروع سری، 2 واحد زیاد شده است). بنابراین، به تساوی زیر خواهیم رسید:

$$\sum\limits_{n = 3}^\infty {{n^2}{a_{n - 1}}{{\left( {x + 4} \right)}^{n + 2}}} = \sum\limits_{n = 5}^\infty {{{\left( {n - 2} \right)}^2}{a_{n - 3}}{{\left( {x + 4} \right)}^n}}$$

در ادامه، چند مثال را درباره استفاده از خواص سری‌های توانی بیان می‌کنیم:

مثال

سری زیر را به فرم استاندارد بنویسید.

$${\left( {x + 2} \right)^2}\sum\limits_{n = 3}^\infty {n{a_n}{{\left( {x + 2} \right)}^{n - 4}}} - \sum\limits_{n = 1}^\infty {n{a_n}{{\left( {x + 2} \right)}^{n + 1}}}$$

حل: ابتدا ضرایب را به داخل سری‌ها منتقل می‌کنیم. بنابراین، به عبارت زیر می‌رسیم:

$$\sum\limits_{n = 3}^\infty {n{a_n}{{\left( {x + 2} \right)}^{n - 2}}} - \sum\limits_{n = 1}^\infty {n{a_n}{{\left( {x + 2} \right)}^{n + 1}}}$$

حال باید توان عبارت $$(x+2)$$ را در داخل دو سری با هم برابر کنیم. بنابراین،

$$\sum\limits_{n = 1}^\infty {\left( {n + 2} \right){a_{n + 2}}{{\left( {x + 2} \right)}^n}} - \sum\limits_{n = 2}^\infty {\left( {n - 1} \right){a_{n - 1}}{{\left( {x + 2} \right)}^n}}$$

برای محاسبه تفریق دو سری، هر دو آن‌ها باید از یک $$n$$ برابر شروع شوند. بسته به سری‌ها، نقطه شروع آن‌ها را می‌توان با روش‌های مختلفی برابر کرد. در این مثال، از آن‌جایی که در سری دوم، اندیس $$n-1$$ وجود دارد، می‌توانیم آن را از $$n=1$$ شروع کنیم. زیرا با این کار، سری تغییری نمی‌کند. بنابراین، مقدار نهایی سری به‌صورت زیر به‌دست می‌آید:

$$\sum\limits_{n = 1}^\infty {\left( {n + 2} \right){a_{n + 2}}{{\left( {x + 2} \right)}^n}} - \sum\limits_{n = 1}^\infty {\left( {n - 1} \right){a_{n - 1}}{{\left( {x + 2} \right)}^n}} = \sum\limits_{n = 1}^\infty {\left[ {\left( {n + 2} \right){a_{n + 2}} - \left( {n - 1} \right){a_{n - 1}}} \right]{{\left( {x + 2} \right)}^n}}$$

مثال

سری زیر را به فرم استاندارد بنویسید.

$$x\sum\limits_{n = 0}^\infty {{{\left( {n - 5} \right)}^2}{b_{n + 1}}{{\left( {x - 3} \right)}^{n + 3}}}$$

حل: همان‌طور که می‌بینیم، عبارات شامل متغیر $$x$$ مشابه هم نیستند و نمی‌توان آن‌‌ها را در هم ضرب کرد. بنابراین، ابتدا باید جمله $$x$$ را به فرم $$x-3$$ در آوریم و داخل سری بیاوریم. این کار را با اضافه و کم کردن $$3$$ به عبارت $$x$$ به‌صورت زیر انجام می‌دهیم:

$$\begin{align*}x\sum\limits_{n = 0}^\infty {{{\left( {n - 5} \right)}^2}{b_{n + 1}}{{\left( {x - 3} \right)}^{n + 3}}} & = \left( {x - 3 + 3} \right)\sum\limits_{n = 0}^\infty {{{\left( {n - 5} \right)}^2}{b_{n + 1}}{{\left( {x - 3} \right)}^{n + 3}}} \\ & = \left( {x - 3} \right)\sum\limits_{n = 0}^\infty {{{\left( {n - 5} \right)}^2}{b_{n + 1}}{{\left( {x - 3} \right)}^{n + 3}}} + 3\sum\limits_{n = 0}^\infty {{{\left( {n - 5} \right)}^2}{b_{n + 1}}{{\left( {x - 3} \right)}^{n + 3}}} \end{align*}$$

اکنون می‌توانیم ضرایب خارج از سری را به داخل منتقل کنیم. با این کار، به عبارت زیر می‌رسیم:

$$\sum\limits_{n = 0}^\infty {{{\left( {n - 5} \right)}^2}{b_{n + 1}}{{\left( {x - 3} \right)}^{n + 4}}} + \sum\limits_{n = 0}^\infty {3{{\left( {n - 5} \right)}^2}{b_{n + 1}}{{\left( {x - 3} \right)}^{n + 3}}}$$

در عبارت بالا، سری اول را نمی‌توانیم از $$n=3$$ شروع کنیم، زیرا جمله $$n-3$$ در آن وجود ندارد که عبارت را در $$n=3$$ صفر کند. بنابراین، هر دو سری را از $$n=4$$ آغاز می‌کنیم:

$$\sum\limits_{n = 4}^\infty {{{\left( {n - 9} \right)}^2}{b_{n - 3}}{{\left( {x - 3} \right)}^n}} + 3{\left( { - 5} \right)^2}{b_1}{\left( {x - 3} \right)^3} + \sum\limits_{n = 4}^\infty {3{{\left( {n - 8} \right)}^2}{b_{n - 2}}{{\left( {x - 3} \right)}^n}}$$

اکنون می‌توانیم دو سری را با هم جمع کنیم:

$$75{b_1}{\left( {x - 3} \right)^3} + \sum\limits_{n = 4}^\infty {\left[ {{{\left( {n - 9} \right)}^2}{b_{n - 3}} + 3{{\left( {n - 8} \right)}^2}{b_{n - 2}}} \right]{{\left( {x - 3} \right)}^n}}$$

نکته

نکته پایانی که در مورد سری‌های توانی می‌توان به آن اشاره کرد، این است که اگر بخواهیم عبارت زیر برای همه مقادیر $$x$$‌ برقرار باشد،

$$\sum\limits_{n = 0}^\infty {{a_n}{{\left( {x - {x_0}} \right)}^n} = 0}$$

باید داشته باشیم:

$${a_n} = 0,\,\,\,n = 0,1,2, \ldots$$