استنباط و آزمون فرض آماری — مفاهیم و اصطلاحات

استنباط و آزمون فرض آماری یک روش استقرایی هستند. به این معنی که با استفاده از امور جزئی به قانون کلی پی‌ می‌بریم. استفاده از اطلاعاتی که یک نمونه از جامعه آماری در اختیارمان می‌گذارد تا رسیدن به قانونی کلی در مورد این جامعه، مراحل یک تحلیل آماری هستند. شما می‌توانید مفاهیم مرتبط با آزمون‌های فرض آماری را به سادگی با مشاهده فیلم‌های مجموعه آموزش آزمون فرض آماری در فرادرس یاد بگیرید.

مفاهیم اولیه در آزمون فرض آماری

هدف اصلی در تحلیل‌های آماری، قضاوت در مورد جامعه آماری (مثلا پارامترهای آن) براساس «آماره» (Statistics) است که بر مبنای مقدارهای نمونه‌ای تصادفی از جامعه محاسبه شده.

فیلم آموزش آمار ریاضی 2 – آزمون فرض در فرادرس

کلیک کنید

از تحلیل آماری در زمینه‌های زیر استفاده می‌شود:

• برآورد برای خصوصیات و روابطی که در جامعه آماری حاکم است.
• انجام آزمون فرض که قضاوتی در مورد جامعه آماری است.

ولی مشکلی که در این میان وجود دارد، کمبود اطلاعاتی است که از جامعه آماری داریم، زیرا نمونه گرفته شده از جامعه آماری همه اطلاعات آن را منعکس نمی‌کند و نمونه فقط می‌تواند بخشی از اطلاعات جامعه آماری را به ما نشان دهد. بنابراین برآورد و آزمون‌ها همواره دارای درجه‌ای از خطا هستند.

البته هرچه اندازه نمونه بزرگتر باشد، اطلاعات بیشتری نیز از جامعه آماری به همراه دارد ولی انتخاب نمونه‌های بزرگ از جامعه آماری، هزینه و زمان زیادی می‌برد. هر چند با استفاده از تحلیل‌های آماری، به کمک یک نمونه با صرفه از لحاظ زمان و هزینه، سعی در برآورد یا انجام آزمون آماری داریم که کمترین خطا را داشته باشد.

در ادامه به تعریف چند واژه می‌پردازیم که در تحلیل‌های آماری زیاد به کار می‌روند.

جامعه آماری (Population)

منظور از انجام یک تحلیل آماری، شناخت در مورد خصوصیات اشیاء یا هویت‌های خاصی است که در یک یا چند ویژگی مشترک هستند و تنها مقدار این ویژگی‌ها برایشان متفاوت است. این اشیاء و هویت‌ها، جامعه آماری را در موضوع مورد تحقیق تشکیل می‌دهند.

توزیع آماری (Statistical Distribution)

در بحث تحلیل آماری، توزیع آماری نشان می‌دهد که مقدارهای مربوط به ویژگی‌ها، به شکل خاصی در بین اعضای جامعه توزیع شده‌اند. به این ترتیب می‌توان احتمال این‌که یک نمونه تصادفی برابر با یک مقدار مشخص یا در یک فاصله از اعداد حقیقی قرار بگیرد را محاسبه کرد. توزیع آماری دارای خصوصیاتی است که به آن پارامترهای توزیع آماری می‌گویند. برای مثال آگاهی از این که توزیع داده‌ها در جامعه آماری از توزیع نرمال پیروی می‌کند، به ما یاری می‌رساند تا جامعه‌ آماری را بهتر شناخته و مقدارهای محتمل در چنین جامعه‌ای را حدس بزنیم. به منظور آشنایی با متغیر تصادفی و توزیع‌های آماری به مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال مراجعه کنید.

پارامترهای جامعه آماری (Statistical Parameters)

هر توزیع آماری دارای ویژگی‌های خاصی است. این ویژگی‌ها که می‌توانند به شکلی منحصر بفرد، توزیع مقدارها در جامعه آماری را نشان دهند، پارامتر جامعه آماری نامیده می‌شود. برای مثال میانگین و واریانس می‌توانند پارامترهای توزیع آماری جامعه باشند.

نمونه تصادفی (Random Sample)

نمونه تصادفی، با انتخاب بعضی از اعضای جامعه آماری به صورت کاملا تصادفی حاصل می‌شود. مبنای برآورد پارامترهای جامعه آماری، مقدارهای حاصل از نمونه تصادفی است. نمونه‌های تصادفی معمولا مستقل از یکدیگر و از جامعه آماری یکسانی انتخاب می‌شوند. نمونه تصادفی به حجم n را به صورت $$X_1,X_2,\ldots,X_n$$ نشان می‌دهیم. از آنجایی که از قبل مقدارهای این نمونه مشخص نیست، به آن‌ها متغیرهای تصادفی می‌گویند.

آماره (Statistic)

یک نمونه تصادفی مثل $$X_1,X_2,\ldots,X_n$$ را در نظر بگیرید. تابعی از این نمونه تصادفی که به پارامتر جامعه آماری وابسته نیست، یک آماره محسوب می‌شود. ممکن است توزیع احتمالی برای آماره به پارامتر مجهول جامعه آماری وابسته باشد ولی مقدار آن چنین نیست. برای مثال میانگین یک نمونه تصادفی که با $$\overline X$$ نشان داده می‌شود،‌ یک آماره است. در حالیکه $$\overline X -\mu$$ دیگر آماره نیست زیرا به پارامتر جامعه یعنی $$\mu$$ وابسته است.

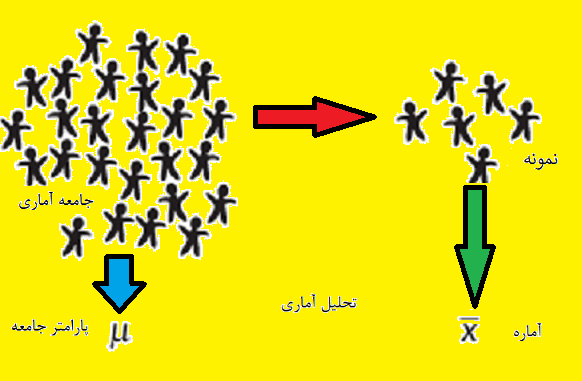
انواع تحلیل‌های آماری

همانطور که گفته شد، هدف از تحلیل آماری، شناخت جامعه آماری براساس مقدارهای حاصل از نمونه‌های تصادفی است. در این میان دو رویکرد در تحلیل‌های آماری بوجود می‌آید.

فیلم آموزش آزمون های فرض میانگین جامعه در اس پی اس اس SPSS در فرادرس

کلیک کنید

برآوردیابی

اگر هدف از تحلیل آماری، برآورد پارامتر جامعه آماری باشد بطوری که دقت برآورد نیز قابل محاسبه باشد، «برآوردیابی» (Estimation) انجام شده است. آماره‌ای که برای عمل برآوردیابی به کار گرفته شده نیز «برآوردگر» (Estimator) و نتیجه حاصل از آماره توسط مقدارهای نمونه تصادفی را «برآورد» (Estimate) پارامتر جامعه می‌گویند.

روش‌های مختلفی برای برآوردیابی پارامترهای جامعه آماری وجود دارد. ممکن است برای برآورد پارامتر جامعه آماری به یک نقطه یا مقدار اشاره کرد. این مقدار که توسط نمونه تصادفی ایجاد شده، «برآورد نقطه‌ای» (Point Estimator) برای پارامتر نامیده می‌شود. ولی گاهی از یک فاصله عددی به عنوان برآورد پارامتر جامعه، استفاده می‌شود و با میزان اطمینان مشخصی، اعلام می‌شود که این فاصله شامل پارامتر جامعه است. در این حالت برآورد حاصل را «برآورد فاصله‌ای» (Interval Estimator) برای پارامتر می‌نامند.

برآوردگر نقطه‌ای

به منظور برآورد نقطه‌ای از شیوه‌های مختلفی در آمار استفاده می‌شود. روش‌ «گشتاوری» (Moment) یکی از این روش‌ها است که توسط آماردان انگلیسی «کارل پیرسون» (Karl Pearson)  در سال 1894 به کار گرفته شد. از روش‌های دیگر می‌توان به روش «حداکثر تابع درستنمایی» (Maximum Likelihood Function) اشاره کرد که توسط آماردان انگلیسی «رونالد فیشر» (Ronald Fisher) در سال‌های 1912 تا 1920 مورد استفاده قرار گرفت و قضیه‌های زیادی را براساس آن اثبات کرد.

برای این که نشان داده شود، برآورد، چقدر از پارامتر دور یا نزدیک است، از ملاک‌هایی مانند «میانگین مربعات خطا» (Mean Squared Error) که به MSE نیز معروف است، استفاده می‌شود. به این ترتیب برای مقایسه دو برآوردگر کافی است که مقدار MSE را برای هر یک محاسبه کنیم و برآوردگری را انتخاب کنیم که دارای MSE کمتری است. البته انتخاب بهترین برآوردگر به معیارهای دیگری نیز احتیاج دارد که در این نوشتار به آن‌ها نمی‌پردازیم.

برآوردگر فاصله‌ای

ممکن است برای برآورد پارامتر جامعه، از یک فاصله تصادفی استفاده شود. دو سر این فاصله، توسط توابعی از نمونه تصادفی ساخته می‌شود. بنابراین اگر $$g_1$$ یک سر فاصله و $$g_2$$ تابع مربوط به سر دیگر فاصله اطمینان باشد، خواهیم نوشت:

$$P(g_1(X_1,X_2,\ldots,X_n)<\theta$$

در این حالت می‌گوییم فاصله تصادفی $$g_1$$ تا $$g_2$$ با احتمال $$1-\alpha$$ پارامتر $$\theta$$ را در بر می‌گیرد. از آنجایی که این فاصله براساس نمونه تصادفی محاسبه شده است، با انتخاب نمونه دیگر تغییر خواهد کرد. ولی با توجه به مفهوم احتمال می‌توانیم بگوییم اگر ۱۰۰ فاصله تصادفی برای پارامتر $$\theta$$ براساس ۱۰۰ نمونه تصادفی تولید کنید، $$(1-\alpha)$$ درصد از آن‌ها میانگین جامعه را شامل خواهد شد. همانطور که در تصویر زیر دیده می‌شود اگر خط آبی مقدار واقعی پارامتر جامعه باشد، در بین ۲۰ فاصله اطمینان تولید شده با احتمال ۹۵٪ ، تنها یکی از فواصل، شامل پارامتر جامعه آماری نیست.

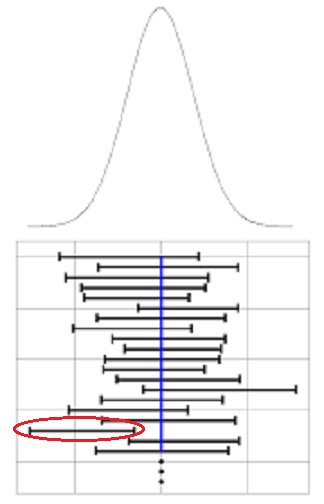
به میزان $$\alpha$$ «سطح معنی‌داری» (significance level) یا «سطح آزمون» (Level of Test) و به $$1-\alpha$$‌ «سطح اطمینان» (confidence level) گفته می‌شود. معمولا سطح معنی‌داری را ۵٪ و یا سطح اطمینان را ۹۵٪ انتخاب می‌کنند. هر چه سطح اطمینان را بیشتر کنید طول فاصله اطمینان یعنی $$g_2-g_1$$ بیشتر می‌شود. در حقیقت بازه‌ای که برای پارامتر جامعه در نظر گرفته شده، دقت کمتری را خواهد داشت. و برعکس هر چه سطح اطمینان کاهش یابد، طول فاصله اطمینان کاهش یافته و دقت بیشتری برای مشخص کردن مقدار پارامتر جامعه آماری فراهم می‌شود.

آزمون فرض آماری

در روش‌های مربوط به آزمون فرض آماری، یک گزاره در مورد پارامتر جامعه آماری مورد بررسی قرار می‌گیرد و برعکس روش‌های برآوردیابی، برای پارامتر جامعه مقداری را محاسبه نمی‌کند.

فیلم آموزش آنالیز واریانس با اس پی اس اس SPSS در فرادرس

کلیک کنید

برای مثال، عبارت زیر نمونه‌ای از گزاره‌ای است که می‌توان برای یک آزمون فرض آماری نوشت:

$$H_0: \mu=5$$

این گزاره بیان می‌کند که میانگین جامعه یا همان $$\mu$$ برابر با ۵ است. گزاره مورد اشاره توسط نمونه تصادفی و روش‌های آزمون فرض سنجیده شده و صحیح یا ناصحیح بودن آن با در نظر گرفتن سطح اطمینان مشخصی، تعیین می‌شود.

معمولا این گونه گزاره‌ها را با حرف H‌ که مخفف کلمه Hypothesis‌ یا فرضیه است، شروع می‌کنند. به همین دلیل گاهی به این گزاره‌ها، فرضیه آماری نیز می‌گویند. اگر با فرض صحیح بودن این گزاره، بتوان توزیع جامعه آماری را مشخص کرد، به آن گزاره، «فرضیه ساده» (Simple Hypothesis) گفته می‌شود و در غیر اینصورت آن را «فرضیه مرکب» (Composite hypothesis) می‌خوانند. برای مثال گزاره زیر یک فرضیه مرکب است.

$$H_0: \mu<5$$

آزمون فرض آماری دارای دو گزاره یا دو فرضیه است. ابتدا «فرضیه صفر» (Null Hypothesis) ظاهر می‌شود که معمولا نظری است که از قبل در مورد پارامتر یا جامعه آماری وجود داشته. برای مشخص شدن اینکه یک گزاره، فرضیه صفر است از علامت $$H_0$$ در ابتدای آن استفاده می‌شود. معمولا هدف از انجام فرض آماری یک محقق این است که به کمک نمونه تصادفی نشان دهد که فرض صفر صحیح نیست. زیرا در غیر اینصورت تحقیق او چیزی بیش از تایید گزاره‌های قبلی در مورد جامعه آماری نخواهد بود.

بعد از فرضیه صفر، «فرضیه مخالف» (Alternate Hypothesis) یا فرض مقابل قرار دارد که هدف محقق از آنجام فرض آماری را نشان می‌دهد. معمولا این فرضیه نقیض فرضیه صفر است و آن را به علامت $$H_a$$ یا $$H_1$$ نشان می‌دهند.

برای مثال فرض مخالف برای فرض صفر قبلی می‌تواند به صورت $$H_a: \mu=6$$ نوشته شود که یک فرضیه ساده است. همچنین می‌تواند به صورت $$H_a: \mu>5$$ باشد که یک فرضیه مرکب است. مهم این است که دو گزاره یا فرضیه صفر و مخالف، همپوشانی در مورد پارامتر جامعه آماری نداشته باشند.

به این ترتیب یک آزمون فرض آماری برای مثلا پارامتر میانگین جامعه آماری می‌تواند به یکی از صورت‌های زیر نوشته شود:

$$\begin{cases} H_0: \mu =a\\ H_1: \mu= b\\ \end{cases}$$

$$\begin{cases} H_0: \mu =a\\ H_1: \mu>a\\ \end{cases}$$

$$\begin{cases} H_0: \mu =a\\ H_1: \mu<a\\ \end{cases}$$

$$\begin{cases} H_0: \mu a\\ \end{cases}$$

$$\begin{cases} H_0: \mu <a\\ H_1: \mu= b\\ \end{cases}$$

...

برای اینکه مشخص شود که آیا براساس نمونه می‌توان فرض صفر را رد کرد باید ملاکی در نظر گرفته شود. در چنین حالتی یک آماره را ملاک قرار دهیم که آن را «آماره آزمون» (Test Statistic) می‌گویند. در نتیجه، با توجه به توزیع آماره‌ آزمون، یک «ناحیه بحرانی» (Critical Region) ساخته می‌شود. البته انتخاب این ناحیه بحرانی بر اساس معیاری است که در ادامه به توضیح آن می‌پردازیم. اگر مقدار آماره آزمون با توجه به نمونه تصادفی در ناحیه بحرانی قرار بگیرد، فرض صفر رد می‌شود. در غیر اینصورت دلیلی برای رد کردن فرض صفر وجود ندارد.

همچنین آستانه مقداری در آزمون فرض که بواسطه آن امکان رد فرض صفر یا عدم رد آن وجود دارد «مقدار بحرانی» (Critical Value) نامیده می‌شود. در ادامه برای روشن شدن موضوع به یک مسئله در همین رابطه می‌پردازیم.

مثال

در یک بازی شانسی، باید یک سکه پرتاب شود. اگر سکه شیر بیاید برنده خواهیم بود و در غیر اینصورت بازنده. برگزار کننده این بازی ادعا دارد که سکه‌اش نااریب است. یعنی احتمال ظاهر شدن شیر با خط برابر است. برای اینکه ادعای برگزار کننده را بررسی کنیم یک آزمون آماری تشکیل می‌دهیم.

اگر p احتمال مشاهده شیر باشد، فرضیه‌های این آزمون آماری به صورت زیر است:

$$\begin{cases} H_0: p =\dfrac{1}{2}\\ H_1: p \neq \dfrac{1}{2}\\ \end{cases}$$

هر دو طرف با هم توافق می‌کنیم اگر در ۱۰ بار پرتاب سکه 5 بار شیر مشاهده شد، سکه نااریب است و در بازی شرکت می‌کنیم و در غیر اینصورت از بازی خارج خواهیم شد. پس اگر X را تعداد شیر در ۱۰ بار پرتاب سکه در نظر بگیریم ناحیه بحرانی به صورت $$X\neq ۵$$ نوشته می‌شود و مقدار بحرانی نیز برابر با 5 است. حال سکه را 10 بار پرتاب می‌کنیم  و تعداد شیرها برابر با ۶ می‌شود.

بنابر نتیجه نمونه تصادفی و ناحیه بحرانی در بازی شرکت نمی‌کنیم و شانس برنده شدن در این بازی را از دست می‌دهیم. ولی شاید در تصمیم‌گیری اشتباه کرده باشیم. جدول زیر به بررسی این گونه خطاها می‌پردازد. ستون‌ها، نتایج آزمون آماری (تصمیم ما) و سطرها، واقعیت در مورد نااریب بودن سکه را نشان می‌دهند.

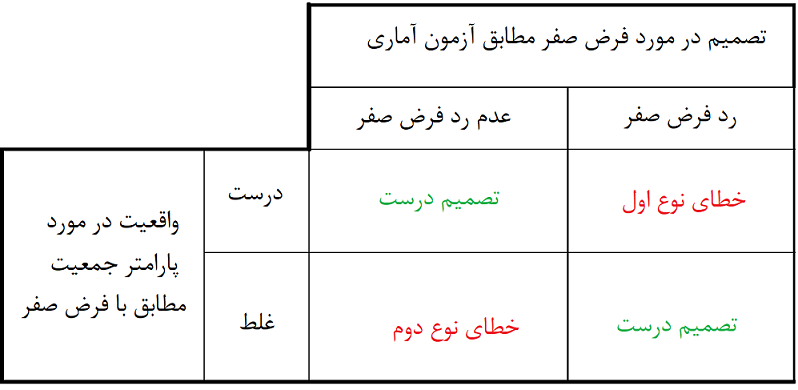
در این بازی با توجه به تصمیماتی که براساس مقایسه بین واقعیت و تصمیم ما وجود دارد ممکن است دچار دو گونه خطا بشویم. خطای نوع اول عدم شرکت در یک بازی عادلانه است که در نتیجه شانس برنده شدن در آن را از دست داده‌ایم. خطای نوع دوم نیز شرکت در بازی است که عادلانه نیست. در نتیجه شکست در این بازی دور از انتظار نخواهد بود.

در چنین حالتی احتمال خطای نوع اول را $$\alpha$$ و احتمال خطای نوع دوم را $$\beta$$ می‌نامند. توان آزمون نیز به صورت $$1-\beta$$ قابل محاسبه است که همان احتمال رد فرض صفر به حق است. به بیان دیگر توان آزمون نشان می‌دهد با چه احتمالی، تصمیم درست در رد فرض صفر اتخاذ شده. توان آزمون در این مثال احتمال عدم حضور در یک بازی ناعادلانه را نشان می‌دهد.

با توجه به مفهوم احتمال خطای نوع اول، ناحیه بحرانی را می‌توان محدوده‌ای وابسته به آن در نظر گرفت. هر چه احتمال خطای نوع اول را کاهش دهیم، ناحیه بحرانی کوچک‌تر شده و امکان رد فرض صفر ضعیف‌تر می شود. و برعکس اگر خطای نوع اول را افزایش دهیم، در بیشتر موارد آزمون آماری به رد فرض صفر رای خواهد داد. در نتیجه معمولا احتمال خطای نوع اول را در کارهای صنعتی ۵٪ و برای امور پزشکی و حساس ۱٪ در نظر می‌گیرند.

لازم به یادآوری است که بیشتر آزمون‌های آماری استاندارد، دارای حداکثر توان آزمون هستند یعنی با فرض ثابت بودن خطای نوع اول در سطح ۵٪، خطای نوع دوم آن‌ها از هر آزمون دیگری کمتر است.